必然-可能半三支概念①

魏玲，王振，祁建军，任睿思

1.西北大学 数学学院， 西安 710127； 2.西安电子科技大学 计算机科学与技术学院， 西安 710071；3.西北大学 概念、 认知与智能研究中心， 西安 710127

形式概念分析(Formal concept analysis， FCA)作为有效的、 极具潜力的知识发现工具， 于1982年由德国数学家Wille 首次提出， 用于概念的发现、 排序和显示[1-2]． Wille将数据描述为形式背景， 并定义了一对导出算子， 由此生成形为(外延， 内涵)二元对的形式概念， 继而生成作为该理论核心数据结构的概念格． 概念格是根据形式背景中对象与属性之间的二元关系建立的一种概念层次结构， 生动简洁地体现了概念之间的泛化与特化关系． 目前FCA的主要研究方向有属性约简[3-7]、 规则获取[5，8]以及向三支概念分析[9-11]、 三元概念分析[12-14]的拓广等． 同时该理论还在港口危险品管理、 智慧城市等领域得到了成功的应用[15-17]．

三支概念分析(Three-way concept analysis， 3WCA)是将三支决策理论(Three-way decision， 3WD)[18]中的三分思想应用于FCA而新产生的一种进行知识发现的理论[9-10]． 与形式概念一样， 三支概念也表现为(外延， 内涵)二元对的形式， 但区别于形式概念， 三支概念的内涵/外延为一个正交对[19]， 用于刻画属性集/对象集的三分． 因此3WCA既具有FCA的基本表现形式和具体研究内容， 也体现了3WD的“三分而治”思想． 自 2014 年提出以来， 其思想逐渐为知识发现研究领域的研究人员所接受， 研究主题与理论成果也越来越多， 如： 三支概念格属性约简[20-21]、 三支概念格构建[22-24]、 三支规则获取[25]、 三支概念学习[26]、 三支概念格的特征分析[27]以及三支概念格之间的关系研究[28]等．

三支概念从共性这一角度， 同时考虑对象与属性之间“共同具有”以及“共同不具有”正、 负两方面的信息． 但在某些实际问题中， 共性信息可能不那么重要， 比如在团队合作问题中， 我们不仅需要知道一个团队可以合作完成哪些任务， 还需要关注哪些任务仅可由该团队的成员完成， 这就需要其他模态算子为我们提供的诸如必然信息等其他视角的信息， 因此结合不同的模态算子来实现信息的多视角刻画就十分有意义． 其次， 三支概念的外延与内涵存在着较为严苛的双向对应， 故三支概念的获取也较为复杂， 因此将FCA中半概念[29-30]的单向对应思想引入3WCA也显得十分有意义． 基于此， 本文结合必然算子与可能算子， 利用区间集[31]提出必然-可能三支算子， 并定义必然-可能半三支概念， 进而生成必然-可能半三支概念格．

1 基础知识

本节给出正交对、 区间集以及3WCA的一些基本概念与性质．

对于任意非空论域U，U的幂集记为P(U)，U的幂集的笛卡尔积记为DP(U)， 即

DP(U)=P(U)×P(U)

对于任意的(A1，B1)，(A2，B2)∈DP(U)， DP(U)上的包含、 并、 交分别定义为

特别地， 对于(A，B)∈DP(U)， 如果A∩B=∅， 那么称(A，B)为一个正交对．

U上的区间集为

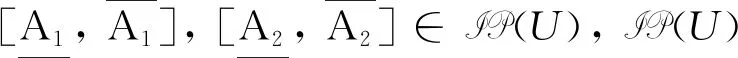
3WCA的数据基础是形式背景．

定义1[2]称三元组(G，M，I)为一个形式背景， 其中G={g1，g2， …，gp}为对象集， 每个gi(i≤p)称为一个对象；M={m1，m2， …，mq}为属性集， 每个mj(j≤q)称为一个属性．I⊆G×M为G和M之间的二元关系， 若(g，m)∈I， 则称对象g具有属性m．

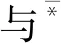
其中c表示集合的补集， 即Ic=G×M-I．

特别地， 对于任意的g∈G，m∈M， 记{g}*为g*， {m}*为m*．

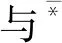
若X<·=(A，B)且(A，B)·>=X同时成立， 则(X， (A，B))称为(G，M，I)的一个对象导出三支概念， 简称为OE-概念， 其中X称为OE-概念的外延， (A，B)称为OE-概念的内涵．

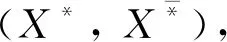
((X，Y)，A))称为(G，M，I)的一个属性导出三支概念， 即AE-概念， 当且仅当(X，Y)·>=A与A<·=(X，Y)同时成立． (X，Y)称为AE-概念的外延，A称为AE-概念的内涵．

所有OE-概念组成的集合OEL(G，M，I)可形成一个完备格， 称之为对象导出三支概念格(简称OE-概念格)． 对偶地， 所有AE-概念形成的完备格称为属性导出三支概念格AEL(G，M，I)(简称AE-概念格)． OE-概念格及AE-概念格上的偏序关系及上、 下确界具体可参见文献[9-10]．

例1表1为形式背景(G，M，I)， 其中对象集G={1， 2， 3， 4}为4名学生的集合， 属性集M= {a，b，c，d}为4个问题的集合． 表1中“1”表示学生能解决该问题， “0”则表示不能， 如： 学生1能解决问题a，c，d， 不能解决问题b． 表1形式背景的OE-概念格、 AE-概念格分别如图1、 图2所示．

表1 形式背景(G， M， I)

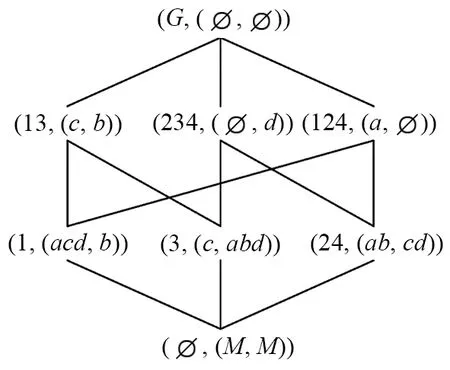
图1 表1的OE-概念格

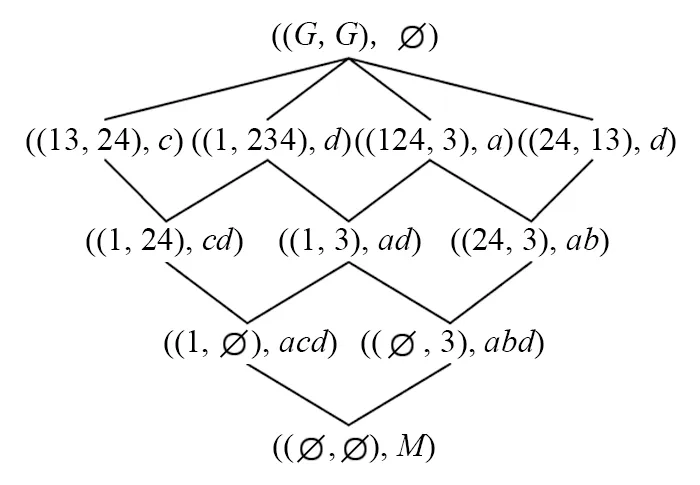
图2 表1的AE-概念格

下面以(13， (c，b))为例解释OE-概念的语义． 该概念表明： 学生1与3都可以解决的问题是c， 都不能解决的问题是b， 而能解决c且不能解决问题b的学生也恰为1与3． {c}∪{b} 的补集中的问题a，d则是学生1与3具有差异的问题． 所以OE-概念清晰、 完整、 准确地反映了一个对象子集的正、 负两种共性与差异性．

AE-概念的解释与OE-概念类似， 只不过是从属性角度出发， 考虑一个属性子集被对象子集共同具有以及共同不具有的情况．

此外， 一些研究人员从模态逻辑的角度， 将*算子称为充分算子， 并陆续提出必然算子、 可能算子以及对偶充分算子等概念[29-30]．

给定形式背景(G，M，I)， 对于任意X⊆G，A⊆M， 必然算子□定义为

X□={m∈M|m*⊆X}

A□={g∈G|g*⊆A}

可能算子◇定义为

X◇={m∈M|m*∩X≠∅}

A◇={g∈G|g*∩A≠∅}

以例1中的对象子集{1， 2}为例， {1， 2}□={d}表明： 能解决问题d的学生一定在学生1与2之中， {1， 2}◇=M表明： 学生1和2能解决所有问题．

必然算子与可能算子的性质如下：

性质1[33-34]设(G，M，I)为一个形式背景， 对于任意X，X1，X2⊆G，A，A1，A2⊆M， 有：

(i)X□⊆X◇，A□⊆A◇；

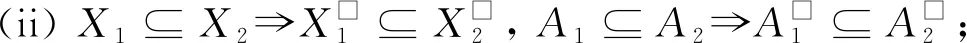
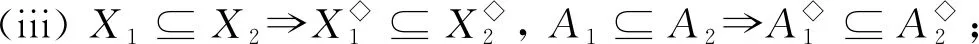
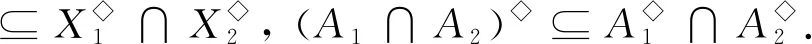
2 对象导出必然可能半三支概念

3WCA从正、 负两方面同时考虑共性， 利用正交对实现对象集属性集的三分． 事实上， 不同的模态算子从不同的角度刻画不同的信息， 并且不同模态算子之间也存在着内在关系， 如： 必然算子与可能算子间的包含关系， 使得我们可以结合两种不同的模态算子， 利用区间集等工具， 定义新的三支算子来获取多视角信息， 并实现对象集属性集的三分．

2.1 对象导出必然可能三支算子

结合必然算子□与可能算子◇， 从对象子集三分属性集的角度， 定义对象导出必然-可能三支算子如下：

ONPE-算子具有如下性质：

性质2设(G，M，I)为一个形式背景， 对于任意X1，X2∈P(G)， 我们有：

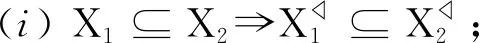
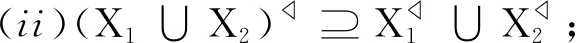
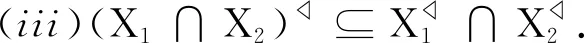
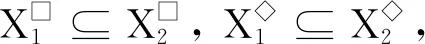
(ii) 由性质1(d)，(e)， 可知

(iii) 由性质1(f)，(g)， 我们有

2.2 对象导出必然可能半三支概念

形式概念分析中， 称形如(X，X*)，(A*，A)的二元对为形式背景(G，M，I)的半概念， 其中X⊆G是任意的对象子集，A⊆M是任意的属性子集． 不难看出， 半概念仅考虑对象子集与属性子集间的单向对应， 而不再强调苛刻的双向对应． 基于这种思想， 我们利用ONPE-算子， 定义对象导出必然-可能半三支概念为：

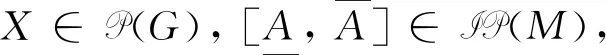
对于对象子集X⊆G， 区别于OE-算子获取的共有属性， ONPE-算子可以同时获取必然属性X□与可能属性X◇， 并形成属性集M上的一个区间集[X□，X◇]， 这个区间集可将M分为3部分： 正域POSX=X□、 负域NEGX=M-X◇以及中间域BNDX=X◇-X□． 并且POSX，NEGX和BNDX两两互不相交， 形成M的一个弱三划分．

例2表1形式背景下所有的ONPSE-概念如表2所示．

表2 表1的ONPSE-概念

以(12， [d，M])， (14， [d，M])为例解释ONPSE-概念的语义． 概念(12， [d，M])表明： 能解决问题d的学生在学生1与学生2当中， 学生1和学生2可以合作解决所有的问题． 类似地， 概念(14， [d，M])表明： 能解决问题d的学生在学生1与学生4当中， 学生1和学生4可以合作解决所有的问题． 结合两个ONPSE-概念， 我们进一步可知， 能解决问题d的学生是学生1， 符合概念(1， [d，acd])所反映的信息．

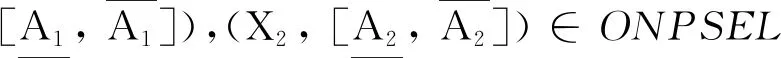
称ONPSEL(G，M，I)为(G，M，I)的对象导出必然-可能半三支概念格， 简称为ONPSE-概念格． 定理1给出其上、 下确界， 并证明其是一个完备格．

定理1ONPSEL(G，M，I)是一个完备格， 其上、 下确界分别为：

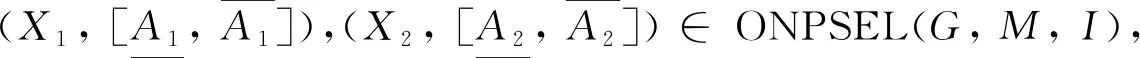
则X1⊆X且X2⊆X， 故X1∪X2⊆X， 因此

例3表1的ONPSE-概念格如图3所示．

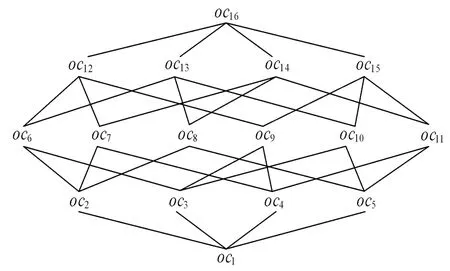
图3 表1的ONPSE-概念格

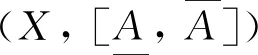
定理2ONPSEL(G，M，I)≅P(G)， 其中P(G)为G的幂集格．

3 属性导出必然-可能半三支概念

3.1 属性导出必然-可能三支算子

结合必然算子□与可能算子◇， 从属性子集三分对象集的角度研究属性导出必然-可能半三支概念． 因与第2节类似， 本节证明省略． 首先， 定义属性导出必然-可能三支算子如下：

ANPE-算子具有如下性质：

性质3设(G，M，I)为一个形式背景， 对于任意A1，A2∈P(M)， 我们有：

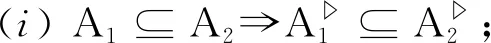
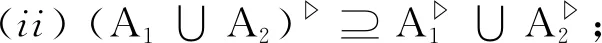
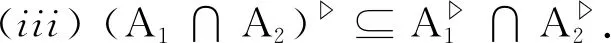
3.2 属性导出必然-可能半三支概念

ANPE-算子可以生成属性导出必然-可能半三支概念， 简称ANPSE-概念．

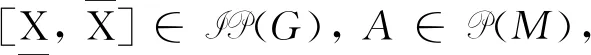
ONPSE-概念与ANPSE-概念统称为必然-可能半三支概念， 简称为NPSE-概念．

类似于ONPE-算子， 对于属性子集A⊆M， 可以利用ANPE-算子得对象集G上的一个区间集[A□，A◇]， 这个区间集可将G分为3部分： 正域POSA=A□、 负域NEGA=G-A◇以及中间域BNDA=A◇-A□． 并且POSA，NEGA和BNDA互不相交， 形成G的一个弱三划分．

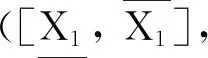
称ANPSEL(G，M，I)为(G，M，I)的属性导出必然-可能半三支概念格， 简称为ANPSE-概念格．

定理3ANPSEL(G，M，I)是一个完备格， 其上、 下确界分别为

例4表1的所有ANPSE-概念如表3所示， ANPSE-概念格如图4所示．

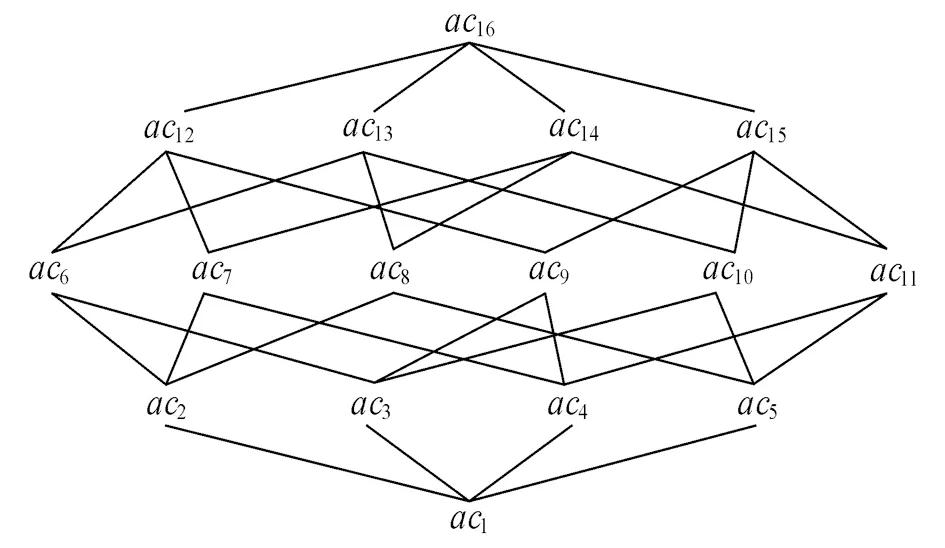
图4 表1的ANPSE-概念格

表3 表1的ANPSE-概念

以([234，G]，abc)为例解释ANPSE-概念的语义． 概念([234，G]，abc)表明： 问题a，b，c可被所有学生合作解决， 学生2，3，4能解决的问题在a，b，c当中． 并且G与{2， 3， 4}的差集中的学生1还能解决其他问题， 如概念([∅， 1]，d)表明： 学生1还能解决问题d．

由ANPSE-概念定义， 可得以下结论：

定理4ANPSEL(G，M，I)≅P(M)， 其中P(M)为M的幂集格．

4 结语

本文基于多视角信息获取这一想法， 结合必然算子与可能算子， 从对象或属性这两种不同的角度出发， 定义了对象导出与属性导出必然-可能三支算子， 并结合形式概念分析中半概念的单向对应思想， 获取了对象导出与属性导出必然-可能半三支概念， 拓广了三支概念的语义．

事实上， 对象与属性作为两种不同的研究角度， 生成的两种必然-可能半三支概念的语义解释与应用场景也有所不同， 如在形式概念分析与知识空间理论结合的研究[35-36]中， 从对象或属性出发可分别看作是问题驱动或技能驱动这两种截然不同的研究方向， 因此如何结合上述研究成果， 对两种必然-可能半三支概念的语义与应用做进一步研究就很有意义． 本文仅从正面结合必然算子与可能算子获取了多视角的信息， 而负信息也很重要， 因此如何从负面结合必然算子与可能算子来获取信息也十分有意义． 并且必然算子与可能算子与双论域粗糙集[37-38]的下、 上近似有着紧密联系[39]， 因此本文获取的必然-可能半三支概念对双论域粗糙集的知识可视化也有所帮助， 如： 我们可以从ONPSE-概念格迅速获取双论域粗糙集的可定义集与不可定义集， 因此如何将本文研究内容与双论域粗糙集结合也很重要． 最后， 其他模态算子的结合研究也十分有意义， 如文献[40]结合充分算子与可能算子探讨了共同-可能粒描述． 这些都是我们未来的研究方向．