分数阶二维线性系统的奇点类型及其邻域内的轨道性态

罗 静，冀小明

（1.重庆师范大学数学科学学院，重庆 401331；2.西南民族大学预科教育学院，四川 成都 610041）

近几十年以来，分数阶微分方程被广泛地应用到了众多自然科学和工程学领域，如:流体力学和热力学中的反常扩散和热传导现象[1-4]、结构力学中的粘弹性现象[5-8]、通信领域中的信号和图像处理[9-11]、控制理论中的系统控制[12-13]、磁力学[14-16]以及生物科学[17-19]等其他众多领域和学科之中.由于自然界和工程中存在大量的分数维现象，从而整数维理论已经不再适用于这些问题的解决，所以人们引入分数阶微积分使之不受整数维度的限制，这也是分数阶微分方程(特别是分数阶动力系统)越来越受到人们重视的主要原因.相对于整数阶微分方程而言，分数阶微分方程的求解研究工作往往比较困难，正如文献[20]中作者所说的那样，目前大多数关于分数阶微分方程的研究工作主要集中在正解的存在性研究，与这类研究不同的是本文的工作将立足于分数阶动力系统奇点(即平衡点)分类情况及其相关性质方面的探索与研究.

本文将借助于一系列的线性变换和Laplace 变换，再利用Mittag-leffler 函数的敛散性质来研究下列分数阶线性系统(动力系统)奇点的分类情况以及各种奇点邻域内轨道的动力学性态.

这是一个众所周知的经典线性系统，它的奇点分类以及奇点周围的轨道的动力学性态早为人们所熟悉.在研究系统(2)时，人们通常将其转化为后研究系统的平面相图，然而对于系统(1)，如果用类似的方法将其转化为后，我们不知道这个式子中的在分数阶微积分领域表示什么? 更不知道它有什么几何意义或物理意义?因此人们无法用类似的方法来研究这类分数阶动力系统，这也是为什么长期以来没有全面地研究过这类动力系统的奇点分类及其相应的动力学性态的主要原因.直到2013 年，马玉田博士在李常品教授的指导下，在他的博士论文[21]中研究过系统(1)的奇点，给出了分数阶动力系统的线性化定理，并指出原点O是系统(1)的双曲平衡点(即双曲奇点)，但由于受到技术的限制，他们并没有对奇点O进行分类讨论，也没有进一步研究平衡点周围的轨道走势和系统(1)相应的动力学性态(即平衡点邻域内轨道的动力学性态及其分布图貌)，我们的工作是在新技术下再次研究该系统的平衡点，进一步完善这些研究内容.

为简单起见，接下来我们将借助于一系列线性变换先把系统(1)转化成便于求解的标准型系统，然后再利用Laplace 变换及其逆变换来进行求解，在整个求解和分析的过程中，线性变换不会改变分数阶动力系统的奇点位置和邻域内轨道的动力学性态.

1 线性变换下分数阶二维线性系统的约化

显然，当detA≠0 时，系统(1)和(3)只有一个奇点(平衡点)，即原点O(0，0).

根据矩阵A的特征值的三种情况，即特征值为共轭复根α ± βi，特征值为一对不相等的实根λ1，λ2和特征值为重实根μ的三种情况，一定可以找到相应的可逆矩阵T，使得T-1AT = J，J就是下列四种类型的矩阵之一

其中:α，β，λ1，2，μ均为实数.

方程(5)两边同时左乘以一个逆矩阵T-1得:

由于在变换式中矩阵的初等行变换不影响线性变换的性质，因此对(16)式中的最后一个矩阵施行两次行变换得:

且在a = δ = μ的情形下，矩阵A的特征根为重实根，否则为不相等的两个实根.

类似于定理1.1 的证明方法，不难证明定理1.2和定理1.3，限于篇幅，这里省略他们的证明过程，只给出具体的线性变换表达式和相应的标准型系统.不难发现，分数阶线性系统的线性变换与整数阶线性系统的变换是一样的，但系统的奇点的类型却不太一样，因此奇点邻域的轨道的性态也就大不一样了. 详情请参见下一节的讨论.

2 线性系统的奇点邻域内轨道的动力学性态及其平面图貌

根据上一节得到的系统(1)的不同标准型，本节也分别讨论这些不同标准型系统的奇点类型及其邻域的轨道的动力学性态.

定理2.1 如果p ＞0，q ＞0，p2-4q ＜0 ，矩阵A的特征值为一对共轭复根λ1，2= α±βi并且在线性变换下系统(1)被约化成如下的标准型

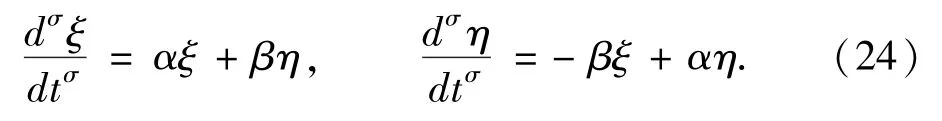
那么原点是该系统的类焦点，且当α ＜0 时，称之为稳定的类焦点；而当α ＞0 时，称之为不稳定的类焦点.

在σ =1 时的整数阶领域，只要再次假设ξ =rcosθ，η = rsinθ， 就可以讨论系统的奇点及其邻域内的轨道性态.众所周知，当σ =1 时，相应的整数阶系统存在三种类型的奇点，即稳定的焦点(α ＜0 时的情形)、不稳定的焦点(α ＞0 时的情形)和中心点(α =0 时的情形)，但在这里却不行，因为分数阶领域不存在复合函数求导的链式法则以及乘积求导的分数阶导数公式，因此人们无法将这类极坐标变换ξ =rcosθ，η = rsinθ嵌入到(24)式(即原(13)式)中进行运算.这是一个非常棘手的问题，到了这里，讨论似乎陷入了僵局，这也是为什么前面的研究者们没有针对分数阶动力系统进行全面研究的主要原因.如果像文献[22-23]中的做法那样，我们利用Laplace 变换及其逆变换对系统(24)式直接进行求解，然后利用参数作图的方法，反构奇点周围(即邻域内)的轨道走势，那就可以进一步讨论轨道的动力学性态和系统的平面图貌了.下面给出定理2.1 的证明过程.

证明:将系统(24)式两边施行Laplace 变换得:

当然，把(29)式代入线性变换式(11)和(12)，也能求出原系统(1)的精确解，这里省略这部分讨论，只讨论系统奇点及其邻域内轨道的性态. 把t看着参数，利用参数绘图法，通过(29)式，用数学软件绘出了系统(24)的平面相图，见图1(a)和(b).

由于当α ＜0 时Mittag-Leffler 函数收敛，而当α ＞0 时Mittag-Leffler 函数发散，故当α ＜0 且t→+∞时ξ(t)→ 0，η(t)→ 0.又当α ＞0 且t→+∞时ξ(t)→+∞，η(t)→+∞.从图 1(a)和(b)也可以看出这一点.

图1 稳定的或不稳定的类焦点及其邻域内的轨道走势Fig.1 Stable or unstable focus-like point and track trends in its neighborhood

把图1 与σ =1 时的整数阶系统相图相比较，不难发现，该类型的奇点周围的轨道并没有螺旋形进入奇点或离开奇点的特征，只有非常接近奇点的地方才稍微有螺旋的趋势，所以该类型的奇点不能像在整数阶系统那里那样被称为焦点，但它的性质非常接近焦点，因此我们称这类奇点为类焦点，当α ＜0 时，称之为稳定的类焦点；当α ＞0 时，称之为不稳定的类焦点.

定理2.2 如果q ＞0，p =0 ，矩阵A的特征值为一对共轭虚根，这相当于上一情形中α =0 的情况，此时系统(1)的标准型为

那么原点是该系统的螺旋型吸引点，且当β ＜0时，轨线逆时针方向趋近于原点，称之为正螺旋型吸引点；而当β ＞0 时，轨线顺时针方向趋近于原点，称之为反螺旋型吸引点.

证明:令ξ(0 )= c1，η(0 )= c2， 然后对(30)式进行Laplace 变换可得:

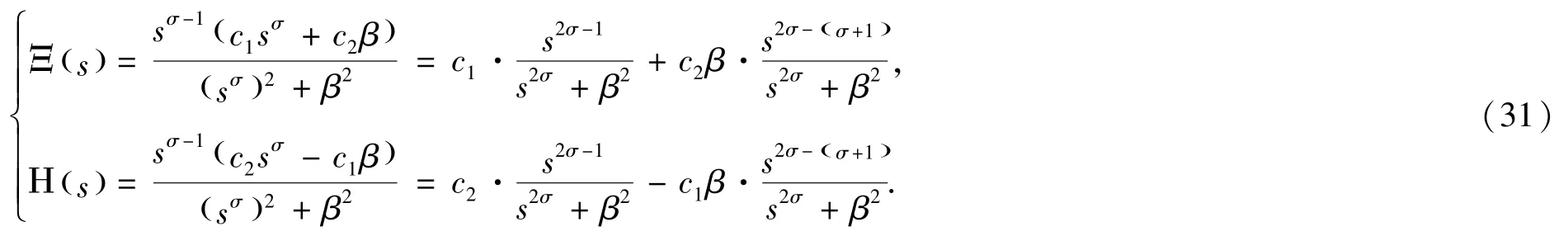
再对(31)式施行Laplace 逆变换后把Mittag-Leffler 函数转换成级数可得:

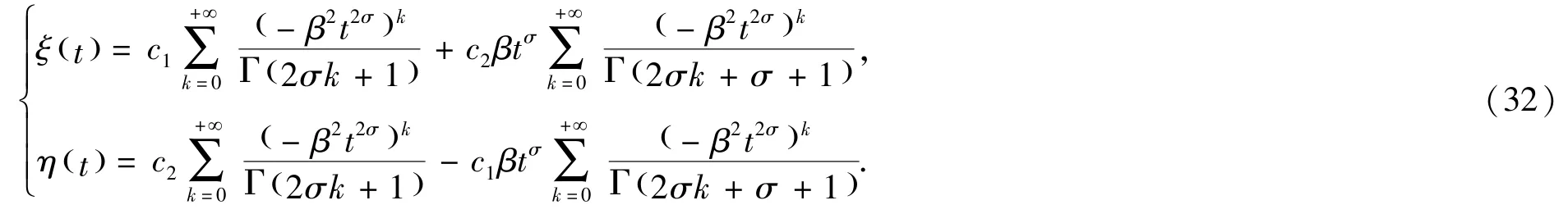
利用(32)绘出系统(30)的平面相图，见图2(a)和(b). 由于(32)式中的级数都是交错级数，始终是收敛的，即当t→+∞时ξ(t)→ 0，η(t)→ 0.

图2 正螺旋型和反螺旋型吸引点及其邻域内轨道的走势Fig.2 Positive and inverse spiral attraction points and track trends in its neighborhood

所以，奇点周围的轨道都螺旋式地趋近于奇点，只是趋近的方向不同罢了.当β ＜0 时，逆时针方向趋近于原点；当β ＞0 时，顺时针方向趋近于原点.我们把这类奇点称之为螺旋型吸引点，逆时针的为正螺旋型，顺时针的为反螺旋型.由此可以看出，分数阶线性系统没有中心点(即中心型奇点)，从而没有闭轨道存在，也就导致这类分数阶微分方程组没有周期解，或者说这类分数阶方程不存在周期解，这与文献[22]中的结论相一致，这又是一个线性的分数阶微分方程没有周期解的有力佐证.

定理2.3 如果q ＞0，p ＞0，p2-4q =0 ，矩阵A的特征值为一对重根λ1，2=μ，那么，

1) 当b≠0 (或c≠0 )时，在线性变换下系统(1)被约化成如下的标准型

则原点是该系统的退化结点，且当μ ＜0 时，称之为稳定退化结点；而当μ ＞0 时，称之为不稳定退化结点.

2)当b = c =0 时，取μ = a = δ，系统(1)被约化成如下的标准型

则原点是该系统的奇结点，且当μ ＜0 时，奇点为稳定的，而零解为渐近稳定的；但当μ ＞0 时，奇点和对应的零解均为不稳定的.

下面对定理2.3 的两种情况分别给出证明.

证明:1)当b≠0 (或c≠0 )时，对(33)式进行Laplace 变换可得:

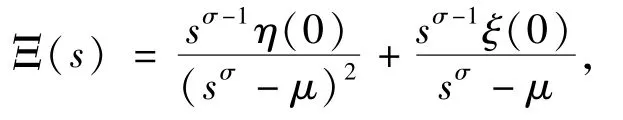
令ξ(0 )= c1，η(0 )= c2， 然后对(35)式进行 Laplace 逆变换可得(33)式的解为:

利用(36)绘出系统(33)的平面相图，见图3(a)和(b).

图3 退化结点及其邻域内轨道的走势Fig.3 Degenerate node and track trends in its neighborhood

由解的表达式知，当μ ＜0，t→+∞时，ξ(t) →0，η(t) →0 ，方程组的零解渐近稳定，所有轨线毫无例外的沿同一个方向趋于奇点，其附近轨线具有这种性态的奇点称为稳定退化结点. 当μ ＞0，t→+∞时，ξ(t) →+ ∞，η(t) →+ ∞，方程组的零解不稳定，这样的奇点称为不稳定退化结点.

2)当b = c =0 时，令x(0 )= c1，y(0 )= c2， 易得(34)式的解为:

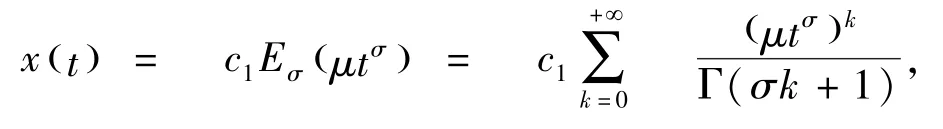
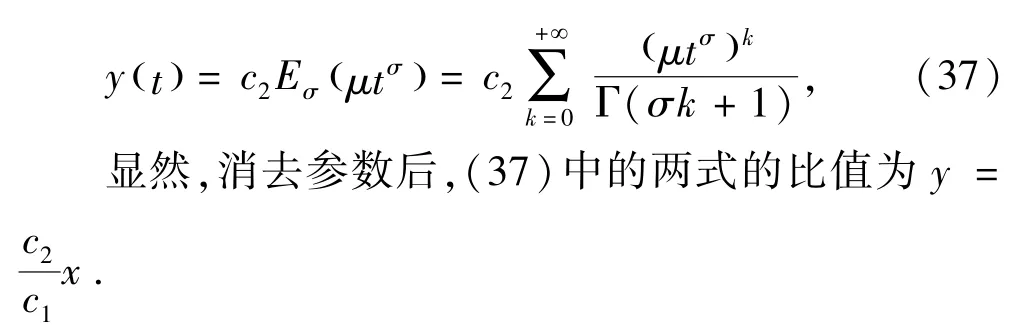
此时，轨线是趋向(或远离)奇点的半射线，轨线均沿确定的方向趋于(或远离)奇点，且不同的轨线其切向各异.当μ ＜0，t→+∞时，ξ(t) →0，η(t) →0 ，故方程组的零解渐近稳定；当μ ＞0，t→+∞时，ξ(t)→+∞，η(t) →+∞，故方程组的零解不稳定.这样的奇点称为奇结点，且与整数阶系统的奇点类型及平面相图相一致.利用(37)绘出系统(34)的平面相图，见图4(a)和(b).

图4 奇结点及其邻域内轨道的走势Fig .4 Singular node and track trends inits neighborhood

定理2.4 如果p ＞0，q ＞0，p2-4q ＞0 ，矩阵A的特征值为一对实根λ1，2，且在线性变换下系统(1)被约化成如下的标准型

那么，当λ1，λ2为异号实根时，原点是该系统的不稳定的鞍点；而当λ1，λ2同为负实根时，原点是该系统的稳定结点；但当λ1，λ2同为正实根时，原点是该系统的不稳定结点.

证明:将系统(38)式两边施行Laplace 变换得:

令ξ(0 )= c1，η(0 )= c2， 然后对(39)式进行 Laplace 逆变换可得(38)式的解为:

当λ1，λ2为异号实根时，利用(40)绘出系统(38)的平面相图，见图5(a)和(b)，这样的奇点称为不稳定的鞍点.

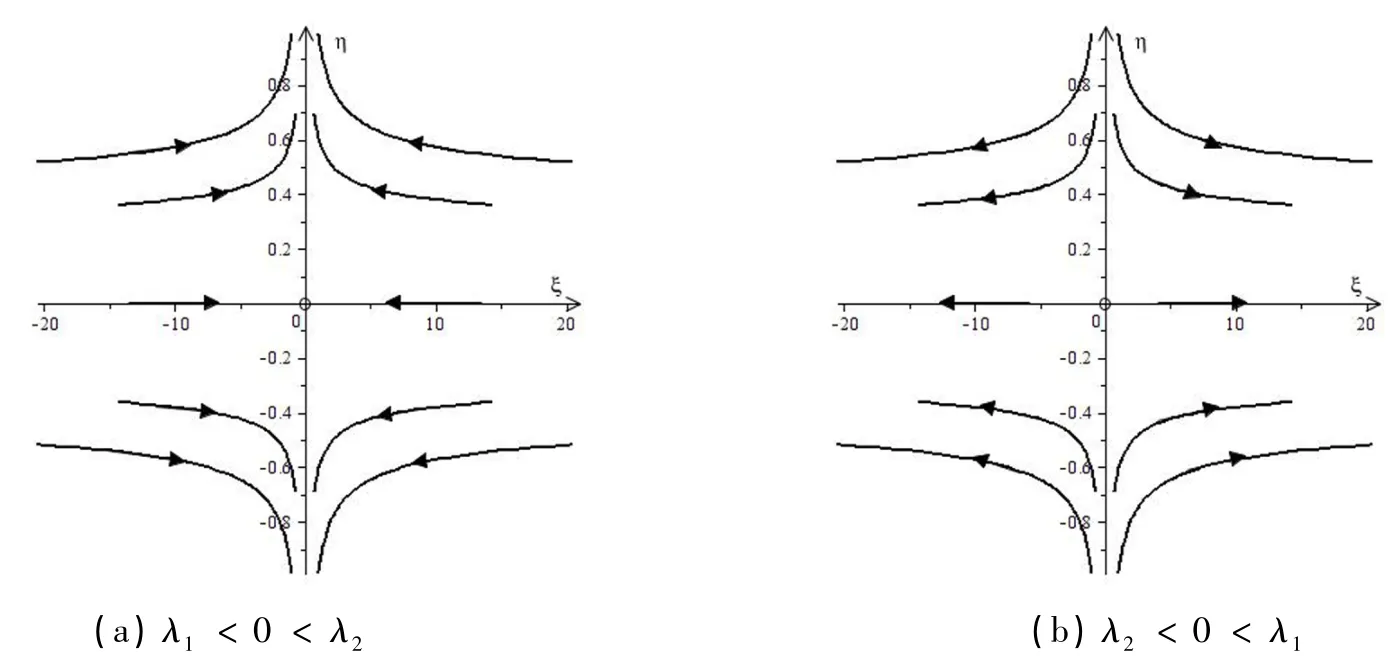
图5 不稳定的鞍点及其邻域内轨道的走势Fig .5 Unstable saddle point and track trends in its neighborhood

当λ1，λ2同为负实根时，即当t→+∞时，ξ(t)→0 ，η(t)→0 ，方程组的零解渐近稳定，系统(38)的平面相图见图6(a)和(b)，这样的奇点称为稳定结点；当λ1，λ2同为正实根时，即当t→+∞时，ξ(t)→+∞，η(t)→+∞，方程组的零解不稳定，这样的奇点称为不稳定结点，系统(38)的平面相图与图6 相同，只是轨线走向与之相反.

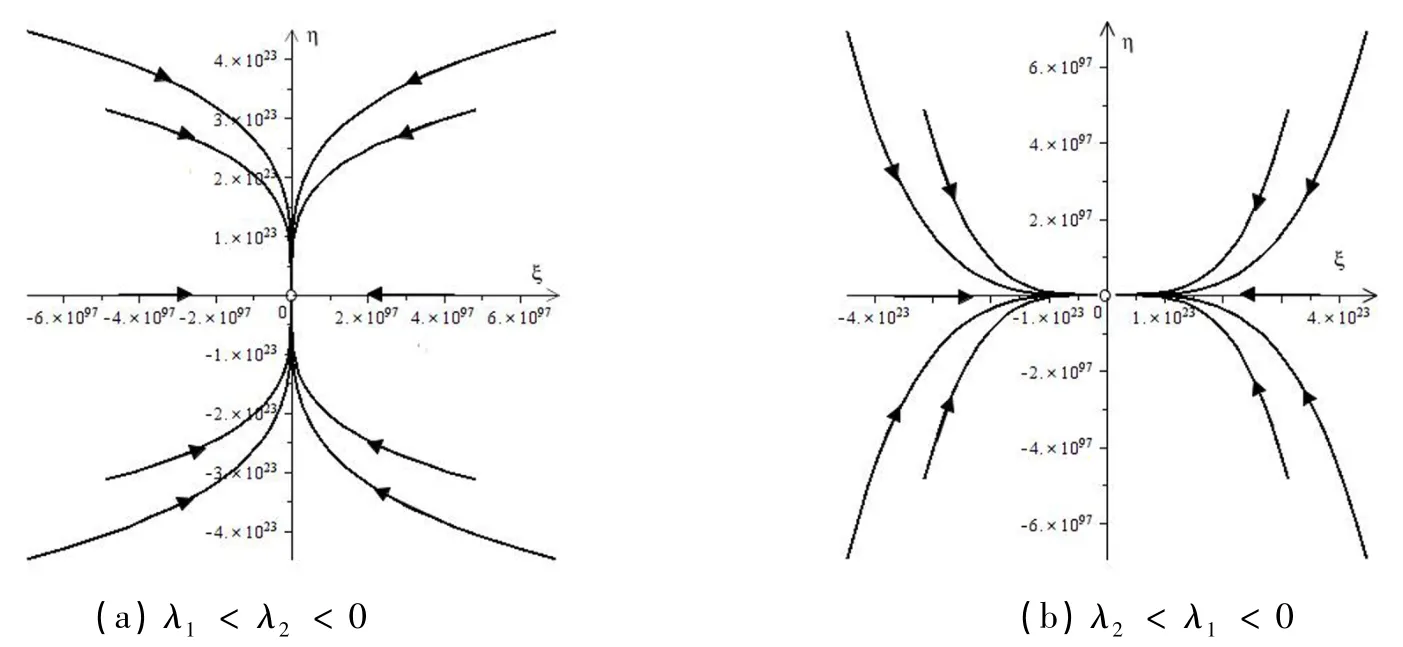
图6 稳定结点及其邻域内轨道的走势Fig.6 Stable node and track trends in its neighborhood