α 粒子被金原子散射的束缚态理论研究

滑亚文，卡盖·索音图，刘以良

（西南民族大学电子信息学院，四川 成都 610041）

费曼认为电子的双缝干涉实验是量子力学的核心问题，它展示了量子力学的一个关键特征:波动性和粒子特性关系.用粒子进行的双缝实验是量子理论中各种基本思想的试验平台[1]，物理学家约恩松在1961 年做了电子双缝干涉实验并得到了明暗相间的干涉图样[2]，再次验证了物质波理论的正确性，即微观粒子同时具有波粒二象性.2013 年美国内布拉斯加-林肯大学的Roger Bach[3]和同事们使用了62 nm宽的狭缝，用能量仅为0.6 keV 的电子通过这些狭缝，他们即使让电子一个一个的通过夹缝，依旧出现了明暗相间的干涉图样.曼彻斯特大学的一个团队用激光来激发原子，之后向它们发射电子，发射的电子会因原子的退激发而获得能量，散射的电子被他们在不同的角度捕捉到，和杨氏实验一样，他们最后依旧得到了干涉模式[3].

第一个原子的杨氏双缝实验是J.Mlynek 等人[4]完成的，实验利用超声气体的膨胀来产生He 原子及部分亚稳态He 原子，He 的λdB是由温度来控制的，通过调节气体容器的温度和调节喷嘴系统来改变温度从而达到改变He 的λdB的目的. 原子先通过一个由20 μm厚的金箔构成的宽2 μm 的狭缝，该原子衍射后飞行64 cm，再通过一个宽为8 μm，长宽分别为2 mm、1 μm 的双缝，各缝边缘的厚度都为 1 μm，原子的物质波经过双缝后在距双缝64 cm 处产生了强度分布条纹，相邻的两条纹间的距离与衍射理论计算的结果符合的较好.

自物质波理论[5-6]提出以来，物理学家不断地设计了一系列思想实验和实物实验以探究波粒二象性的本质.玻尔曾强调[7]:以干涉为特征的粒子的波动性质和以知道粒子通过的裂缝为特征的粒子性质是相互排斥的，他认为在一个实验中人们一次只能看到这两种互补特性中的一种，假设装置探测器来观察光子到底是从哪一条狭缝经过，从而获得路径信息，然而一旦有测量行为，干涉条纹立即消失. 互补性常被认为是物质的波粒二象性，多年来，双缝干涉实验一直被强调为加强互补性的一个很好的例子，哥本哈根学派认为，干涉条纹的消失是由测量仪器的干扰造成的.

经典的单光子双缝实验[8-9]中，直接在双缝那里放探测器会导致光子被探测器吸收，不会形成条纹，所以物理学家利用量子纠缠的特性想到一个巧妙的方法—量子擦除实验[10]，量子擦除实验中没有接收屏，用探测器来取代，即:一个激光发射器，在此之前放一个偏硼酸钡(BBO)晶体，一个光子发射过来后被分解成两个具有相互正交的线偏振、处于纠缠态的光子，让处于下路的光子通过一个前有1/4 的波片的双缝，双缝后面放一个探测器，在上路末尾再放一个探测器.调整距离来保证上路光子先到达，下路光子再经过双缝.光子通过1/4 的波片时做了标记，通过某种手段可以知道光子具体通过了哪条缝. 将上、下路的两个探测器用一个电脑连起来，进行联合计数，进行实验，则发现干涉条纹消失了. 若尝试将路径信息擦除掉，再观察会不会形成干涉条纹. 在上路探测器之前插入一个起偏器，擦除对光子的标记，就无法推测出光子通过的是哪一条缝，完成实验后又发现干涉条纹又回来了.这就说明光的路径信息和干涉条纹是互补的，二者只能取其一.

Dürr[11]等在一个原子干涉仪上做了一个确定路径的实验，即用一束冷原子对光驻波的衍射，可以观察到高对比度的衍射图样.在这个实验中没有用到双缝，也没必要去测定原子的位置，而使用原子的内部态来标记原子束的不同路径，衍射图样会立刻消失.这个实验中没有了测量仪器的不可控干扰，他们提出另一种看法:即用粒子间的量子纠缠来解释干涉条纹的消失，knight[12]也认为干涉条纹的消失与纠缠有关.

本研究中，我们提出了一种以α 粒子为入射粒子通过两个金原子之间的模型，基于量子力学束缚态理论研究了微观粒子波粒二象性的关系，并与夫琅禾费单缝衍射公式bsinθ =(k+1/2)λ进行了比较.

1 量子力学束缚态理论计算方法

以两个原子核的连线为y 轴，将两个原子核连线的中点设成坐标轴的交点(0，0)点，假设α 粒子束缚于y 轴，再由定态薛定谔方程就可以求解出概率密度的极大值[13]，从而得到衍射过程中单个α 粒子经过两个原子核之间时量子化的瞄准距离.

考虑单个α 粒子与两个金原子核的相互作用势能函数，则α 粒子受到的库仑势能为:

上式库仑势的势函数如图1 所示:

图1 势函数Fig.1 Potential function

定态薛定谔方程为:

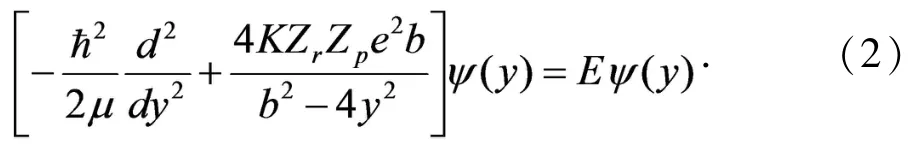
为了得到这个变系数二阶常微分方程的近似解，我们解出了在原点附近方程的解，即:

以下分别是基态波函数、第一激发态波函数和第二激发态波函数:

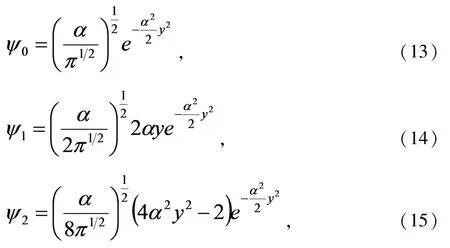
基态概率密度、第一激发态概率密度和第二激发态概率密度分别为:

波函数如图2 所示(A 为基态波函数，B 为第一激发态波函数，C 为第二激发态波函数)，概率密度如图3 所示(A 为基态概率密度，B 为第一激发态概率密度，C 为第二激发态概率密度).

图2 波函数Fig.2 Wave function

根据下式:

基态概率密度、第一激发态概率密度和第二激发态概率密度对应的极大值为:

此外，α 粒子在xoy平面内于不同位置的库仑势能为:

2 结果与讨论

我们参考已有的实验参数，将靶原子间距b设为1 ×10-6m，选取Zr为2 的 α 粒子以及Zp为79 的 Au 原子，在此基础上通过公式(21)和公式(22)计算出了第一和第二激发态的坐标y1= ±1.094 867 3×10-9m和y2= ±1.731 137 2×10-9m，并将此数值作为一级和二级明纹对应的瞄准距离，利用经典动力学理论模拟α粒子的运动轨迹，动力学时间步长设为t =1×10-10s，考虑到α 粒子脱离两个金原子核后，电子的屏蔽作用明显，我们将α 粒子受到的原子力进行了修正，通过测试采用了修正因子0.007，本研究分别采用初速度为 5 000 m/s、6 000 m/s、7 000 m/s、8 000 m/s、9 000 m/s、 10 000 m/s、 11 000 m/s、 12 000 m/s、13 000 m/s、14 000 m/s 的 α 粒子进行入射，在经典的力学方法基础上，以分子动力学计算方法作为参考，根据单个α 粒子在x 轴方向入射后力场中的运动轨迹计算出正弦值.

结果如表1 和表2 所示，表1 为α 粒子单缝衍射一级明纹衍射角的正弦值，表2 为α 粒子单缝衍射二级明纹衍射角的正弦值，我们将量子束缚态理论结果与夫琅禾费单缝衍射公式bsinθ =(k+1/2)λ，(k=1，2，3…)进行了比较[14-15]，结果表明，微观粒子的束缚态理论结果与波动性理论结果相吻合，尤其是以及明纹衍射角的相对误差达到了0.69%，最大相对误差也只有10.43%.然而，与一级明纹相比，二级明纹衍射角正弦值的相对误差明显增加，其最大值达到了27.91%，我们认为这是由于定态薛定谔方程中使用的势能函数为原点附近的近似值，因此越脱离原点其相对误差就越大.

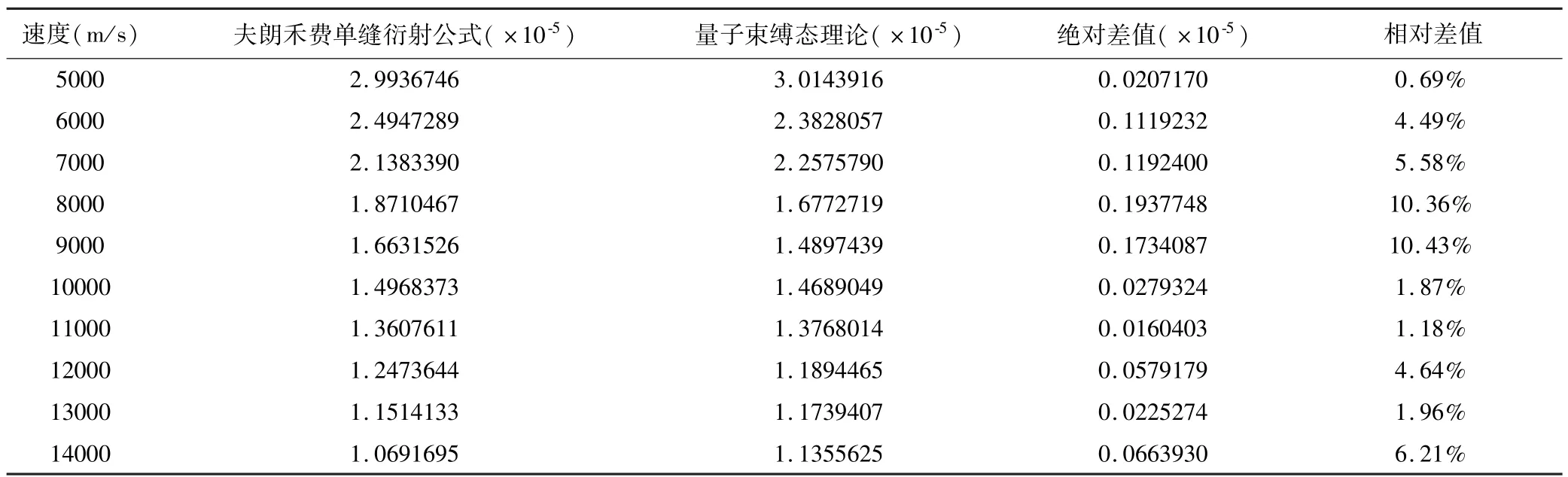
表1 α 粒子单缝衍射一级明纹衍射角的正弦值Table 1 Sine of angle for the first diffraction maximum in the single-slit diffraction of α Particles

表2 α 粒子单缝衍射二级明纹衍射角的正弦值Table 2 Sine of angle for the second diffraction maximum in the single-slit diffraction of α Particles

3 结论

我们建立了一种α 粒子为入射粒子通过两个金原子之间的散射模型，基于量子力学束缚态理论研究了微观粒子波粒二象性的关系，依据束缚态理论，α粒子经过两个金原子核之间时，它的空间分布是量子化的，我们称其为量子化的瞄准距离，结合经典力学理论，量子化的瞄准距离必然会导致出现明暗相间的条纹.通过与夫琅禾费单缝衍射公式进行比较，我们发现微观粒子的束缚态理论结果与波动性理论结果相吻合.然而，量子力学束缚态理论的结果与夫朗禾费单缝衍射公式仍存在一定的相对差值，尤其是二级明纹衍射角正弦值的相对误差明显增加，我们认为这是因为势函数选取了原点附近变系数二阶常微分方程的近似解.

由于该理论采用了变系数二阶常微分方程在原点附近的近似解，因此无法验证高激发态的结果，除此之外，我们的方法无法对衍射暗纹给出很好的解释，这都需要对该理论进行更深入的研究.