狭窄河道泄洪洞与溢洪道联合泄洪三维数值模拟研究
黄桂兵,刁明军,蒋 雷,贾 旺
(四川大学水力学山区河流开发保护国家重点实验室,四川 成都 610065)
挑流消能是通过设置挑坎将具有巨大动能的下泄水流挑射至远离建筑物的下游,凭借水流在空中掺气、破碎以及与水垫塘中水体的碰撞作用来消杀能量,其因结构简单、投资相对较小而在工程中被广泛应用.目前对于挑流消能的研究主要集中在挑流水舌和水垫塘上,采用的方法主要有理论分析、水工模型试验以及数值模拟.刘宣烈[1]等人从理论角度出发分析了空中水舌的运动机理、扩散规律、流速分布以及能量损失;刘士和[2]通过模型试验对挑流水舌断面形态的演化进行了深入研究,并提出了断面面积和湿周的的沿程变化规律.数值模拟在计算能力受到限制时一般采用二维计算,例如沙海飞[3]等人运用两相流的二维紊流模型研究了水舌的入水点等水力特性;刁明军[4]等人从上游库区到下游水垫塘对挑流消能进行了二维全程模拟. 随着计算机的发展,计算能力的提高,数值模拟从二维向三维转变,三维数值模拟更能完整且准确地描述水流特性,叶茂[5]等人通过RNGk-ε模型对导流洞的挑流水舌进行了三维数值模拟,并验证了计算结果与试验数据的可靠性;对于挑流的研究,不仅仅局限在常规体型上,例如薛宏程[6]等人进行的斜切型挑坎挑流水舌的三维数值模拟;闫谨[7]、陈日东[8]和刘冲[9]、李玲[10]等人则通过数值模拟研究了扭曲斜挑坎挑流的形态、流速、紊动能等水力特性.
以往的数值模拟研究大多是在溢洪道或泄洪洞单独泄洪的情况下进行开展的,即模拟计算单个泄洪建筑物,且很少考虑下游河道的不规则性或者将下游河道概化为规则河道进行计算,当溢洪道和泄洪洞联合泄洪时河道内水流紊动比较剧烈,且流态复杂,岸边及水舌附近流态和内部流动对于河床、河岸以及工程的安全意义重大.本文根据下游狭窄河道实际地形建立不规则的河道模型,在扩散型挑坎(溢洪道)与斜切挑坎(泄洪洞)联合泄洪的情况下进行三维数值模拟,对水舌参数、以及河道内流态和内部流动进行分析.
1 模拟工程与数学模型
1.1 工程简介
某工程的泄洪系统由洞式溢洪道和泄洪洞组成,二者轴线基本平行,布置位置较近,洞式溢洪道和泄洪洞轴线距离为45 m.泄洪洞承担泄洪、坝前水位控制、放空水库等功能,泄洪洞进口底板高程765.00 m,孔口尺寸6.5 m ×8 m,泄洪洞由进口段、闸门井段、洞身段、明渠段、消能段组成内设一扇平板检修闸门及弧形工作闸门,平板检修闸门尺寸为6.5 m×9.5 m(宽×高),弧形工作闸门尺寸为6.5 m×8.0 m(宽×高).隧洞段长341.62 m,底坡i =6.7%,隧洞断面为城门洞型,尺寸为 8 m ×12 m(宽 × 高). 明渠段长40 m,底坡i =6.7%. 消能段长度15 m,挑坎为斜切挑坎,挑坎高程736.52 m.
洞式溢洪道由开敞式引渠段、控制段、洞式泄槽段及开敞式挑流消能工等建筑物组成,底板高程775.00 m.控制段长36.35 m,堰体采用WES 实用堰,堰顶高程784.00 m,堰面曲线为 y =0.05651x1.85,后接半径为35 m,圆心角为36.81°的圆弧段.堰顶采用弧门 9.5 m × 15 m(宽 × 高)挡水. 洞式泄槽段长264.96 m,底坡8%,泄槽净宽9.5 m,挑流消能段长21.58 m,挑坎为扩散型挑坎,挑角为20°,挑坎顶高程为750.41 m.
1.2 数学模型
本研究采用Flow-3D 软件进行计算,其Tru-VOF方法是对VOF(Volume of Fluid)技术的进一步改进,能够准确地追踪自由液面的变化情况,使其能够精确地模拟具有自由液面的流动问题,可精确计算动态自由液面的交界聚合和飞溅流动.同时Tru-VOF 方法只计算含有流体的控制单元,使得计算的有效性大大增强,提高了计算效率[11].
内部不可压缩水流运动可由以下连续方程和动量方程描述.

本研究考虑到工程实际情况,采用 RNGk-ε模型[12],该模型可以更好的地处理高应变率及流线弯曲程度较大的流动.模型中k和ε方程如下:

μ1:流体湍动粘度,μeff=μ + μ1;
Gk:由于平均速度梯度引起的湍动能产生项;
αk=αε= 1.39,C1ε= 1.42,C2ε= 1.68.
2 计算区域网格与边界条件设置
2.1 计算模型及网格划分
为了确保数值模拟中泄洪洞和溢洪道的来流条件与实际情况一样,计算域考虑了整个泄洪系统,包括上游库区、进口、泄洪洞和溢洪道、下游库区. 图1为整个计算域的三维几何模型示意图,根据下游河道形状创建下游库区,下游库区底板高程根据河床高程确定为700 m.

图1 计算域三维几何模型示意图Fig.1 Schematic diagram of the 3D geometric model of the computational domain
本次模拟设置网格数目约2 720 万,通过Flow-3D 中Favor 技术对模型网格进行划分,可解决网格模型失真问题.对于挑坎以及水舌附近区域使用网格嵌套的方法进行网格加密.Favor 技术是采用有限差分法离散控制方程为代数方程组进行数值求解,设置最小步长10-8s.图2 为计算域Block 以及网格划分示意图.

图2 计算域Block 以及网格划分示意图Fig.2 Schematic diagram of Block and grid generation in computational domain
2.2 边界与初始条件
上游库区进口设置为流量进口,下游库区出口设置为压力出口,控制下游水位,底部边界为Wall. 同时,为了节省计算时间,对上下游库区进行赋初始场,所赋初始场为预先根据库区形状所创建的水体.
3 结果分析
3.1 洞身流速和水面线
图3、图4 分别给出的是模型试验和数值模拟溢洪道与泄洪洞的沿程水面线、流速结果对比. 从图中可以看数模和物模数据吻合良好,对比结果说明数值模拟计算结果可靠.

图3 物模和数模沿程水面线对比Fig.3 Comparison of the water surface line of physical model and numerical simulation

图4 物模和数模沿程流速对比Fig.4 Comparison of the velocity of physical model and numerical simulation
3.2 水舌形态分析
溢洪道轴线与河道平行,而泄洪洞轴线与河道交角较大.通过模型试验可以看出(图5),水流在溢洪道挑坎的作用下射入空中,在重力的作用下成抛物线跌入水垫塘,在水垫塘中形成淹没冲击射流,水舌呈“马蹄形”、横向扩散充分,水舌落点位于下游河道中间;泄洪洞采用斜切挑坎,水舌达到了纵向拉伸的效果,水舌沿河道纵向落入下游河道. 溢洪道和泄洪洞均有较薄的水舌厚度,与空气掺混作用强,掺气明显.水舌在空气不存在相互碰撞现象.图6 中数值模拟的水舌形态与模型试验水舌形态吻合良好.

图5 试验挑流水舌形态Fig.5 The jet tongue flow pattern of model test

图6 数模挑流水舌形态Fig.6 The jet tongue flow pattern of numerical simulation
3.3 水舌挑距、入水速度及入水角度分析
在实际工程中,水舌落点是关注的重点,即水舌的挑距关系到工程自身的运行安全、下游河道的冲刷等问题.本次研究采用模型比尺为1∶50 的水工模型试验数据作为验证数值模拟可靠性的依据.这里统一使用最大挑距来作为对比的参照,表1 给出了数值模拟和水工模型试验的测量数据,表中数据表明两者吻合程度较高,即数值模拟是可靠的. 数值模拟和模型试验的数据之间也存在一定的误差,其原因主要有以下几点:在非恒定流的计算过程中,水舌的形态具有瞬时特性,挑距是波动的;VOF 方法在对于掺气量大、破裂程度高、紊动比较剧烈水体表面得的捕捉具有局限性;由于水舌厚度较小,对网格的要求非常高,但是网格的尺寸受到计算能力以及时间成本的限制,因此,对于水舌的模拟其精度有一定的限制;水工模型试验中由于水舌的波动,测量数据存在一定误差,且水工模型试验与原型的数据由于比尺效应,也存在一定误差.

表1 水舌挑距对比Table 1 The jet trajectory distance comparison
狭窄河道上的挑流消能,需要考虑水舌对下游河床与河岸的冲刷情况,引起的回流大小,河床的冲刷程度,主要与水舌的入水角度和入水速度有关. 在模型试验中,这些数据很难精确测量,特别是对于非对称水舌形态,因此在工程设计中需要借助理论计算获取.陈华勇[13]在其研究中根据质点抛射体理论和速度分解定理推导出水舌的入水速度公式和入水角度公式,式中h为挑坎顶部到水舌入水处的垂直距离,v0为挑坎处速度,α为挑坎出流速与水平面的夹角,L为水舌挑距.图7 为拟挑距最大位置处数据值模拟结果,表2给出了水舌挑距最大处位置入水流速和入水角度的理论计算与数值模拟结果,从表中数据可以看出,理论计算和数值模拟的结果误差最大为6%,说明其吻合度较好,数值模拟结果相对可靠.

表2 入水流速和入水角度的理论计算和数值模拟对比Table 2 Comparison between theoretical calculation and numerical simulation of water entry velocity and angle

图7 挑距最大位置处水舌Fig.7 The jet tongue at the maximum position of jet trajectory distance
3.4 空中水舌及下游河道流线分析
水舌能量的衰减过程与衰减程度可以给实际工程提供设计参考依据,这些数据在模型试验中难以观察或通过测量手段获取,但借助数值模拟可以轻易获得.图8 为挑距最大位置处水舌的流线图,水舌流速在挑射轨迹上逐渐增加,在入水后急剧降低,溢洪道水舌主流在底板附近衰减4 ~5 m/s,泄洪洞则是5 ~6 m/s.本研究的挑流属于典型的淹没射流,在淹没射流区,射流按照直线扩散开来并卷吸水垫塘内静止液体,在射流的前后各形成一个较大的旋滚区域,由于下游河形状不规则,且两条水舌入水位置比较靠近,因此在本研究中溢洪道水舌射流前后的旋滚区不够明显;在冲击区内射流主流达到或抵近水垫塘底部,随后弯曲,此时流速迅速减小;而在附壁射流区,主流流线紧贴水垫塘底部运动,形成类似附壁射流流态.

图8 挑距最大位置处水舌流线图Fig.8 The streamline diagram at the maximum position of jet trajectory distance
3.5 河道内流态分析
下游水垫塘的主要作用是消杀泄流的绝大部分能量,水舌在入池后形成淹没射流,主流的潜底流速过大可能对对河床基岩造成破坏,同时河道内的洄流和近岸流速过大会导致岸坡淘刷,因此在水舌入池后的池内流态和流速也是工程中关注的重点.图9 为下游河道整体的流线图,从图中可以看出,水舌入水后和水垫塘内水体碰撞,落点附近区域流线交错复杂,说明水流处于翻滚状态,紊动非常强烈;下游水垫塘内主要存在两个大的涡体,即水舌下方区域存在一个逆时针的立轴漩涡,但流速不大,水舌前端靠近右岸存在一个顺时针的横轴漩涡.
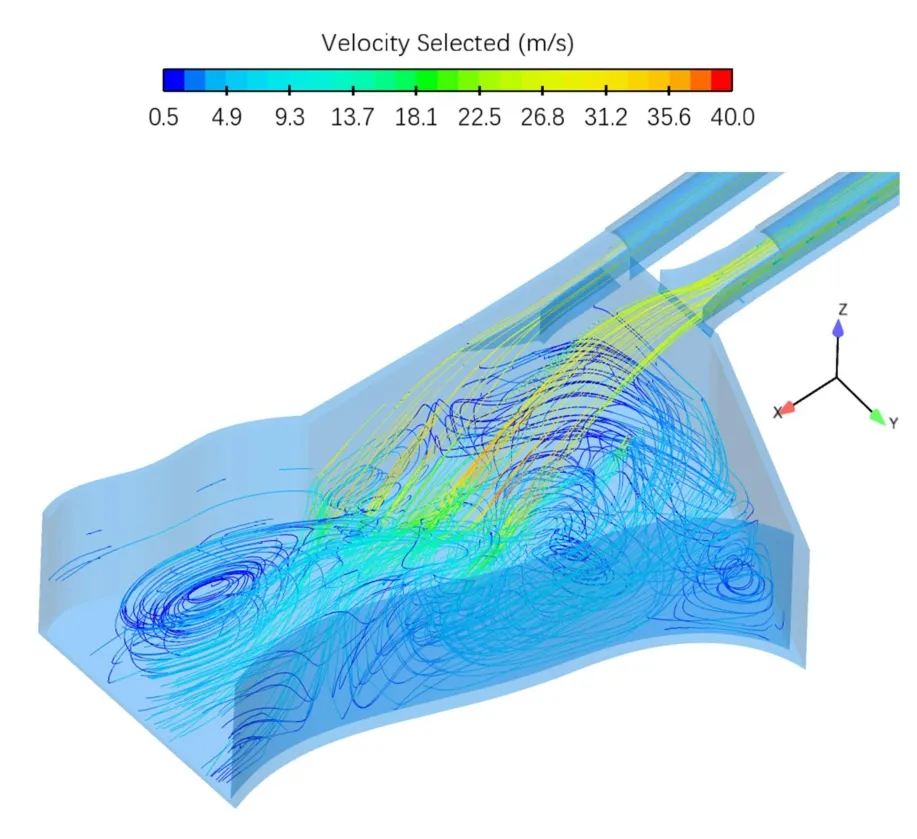
图9 下游河道流线云图Fig.9 Streamline cloud map of downstream river
为了更加清晰准确地了解不同水垫塘高程位置的流速和流场情况,对不同高程位置进行剖切,图10给出了z=-55 m、z=-65 m 和z=-75 m 三个高程断面的流速和流场云图,图中结果表明随着水深的增加,断面上整体的流速在减小,即越接近河床,流速越小;流速最大的地方为水舌主流所在位置,其影响区域也越来越小.
图10(a)中流速云图存在空白部分,主要是由于该区域水流翻滚,水面波动剧烈所导致的,近岸流速在9 m/s 以下;从流场图中可以看出,在x=320 m ~x=400 m 的整个区域内形成一个逆时针的漩涡,漩涡中心位于x=350 m,y=20 m 附近;在x>450 m 的范围内也形成了一个漩涡,漩涡中心位于x=480 m,y=-10 m 附近.
图10(b)中可以看出主流的影响区域位于河道中间,较z=-55 m 断面更小,近岸流速在9 m/s 以下,且近岸流速较大的范围在减小;靠近上游的漩涡范围在增大,漩涡中心较z=-55 m 断面在往下游移动的同时也在往左岸靠近,位于x=375 m,y=32 m 附近,下游漩涡变化不明显.
图10(c)的流速云图中已经不能准确判断主流的所在位置,整个断面上的流速均在9 m/s 以下;从流场图中可以看出,上游漩涡中心继续在往左岸靠近,下游漩涡中心则在往右岸靠近,由于流速减小和河道的不规则,漩涡的范围不能准确判断出来.

图10 下游河道不同高程的流速云图(左)和流场云图(右)Fig.10 Velocity cloud map (left) and flow field cloud map (right) at different elevations of the downstream channel
4 结论
通过与水工模型试验数据的比较,验证了对有多个泄洪建筑物的泄洪系统进行整体模拟是可行的,模拟计算成果是可靠的,数值模拟可以很好的展示沿程水面线、流速、挑流水舌的形态、入水流速与角度、水舌流速的沿程特性以及入水后下游不规则河道内的流场、流态和水力特性.在某种程度上,数值模拟可以获得比模型试验更加全面和准确的数据,为工程设计提供科学依据.同时,数值模拟也能在一定程度上替代模型试验来进行方案比选,有效提升研究效率.

