“源代码”重组：教材例题的引申

文／王 磊

（作者单位：江苏省连云港市海州实验中学）

在做练习时，我们常常会对某道题感觉很熟悉，但又不知在哪里见过，抑或者熟悉知识框架，但是对具体数字陌生。其实，这是非常正常的现象。我们所遇到的题目，有很多是来自教材上的例题，如果将问题情境改变，或者融合一些其他的知识点，就能变成一道新题。教材上的例题往往具有典型性、代表性，凝聚着重要的数学思想，有着较强的示范性，是很多新题的“源代码”。

一、例题再现

（苏科版数学教材八年级下册第131 页例3）已知反比例函数的图像与一次函数y=x+1的图像的一个交点的横坐标是-3。

（1）求k的值，并画出这个反比例函数的图像；

（2）根据反比例函数的图像，指出当x＜-1时，y的取值范围。

解：（1）把x=-3 代 入y=x+1，得y=-2。

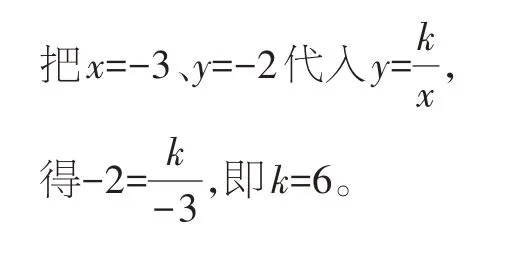
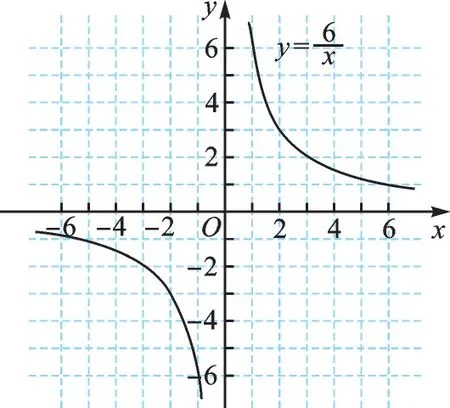
图1

（2）由函数图像知，当x＜-1时，-6＜y＜0。

二、“源代码”重组

一次函数与反比例函数的组合问题，是常见的考试题型。我们要抓住此类题交点的特殊性，利用函数图像的性质来解决。

【基础重组】（2021•山东枣庄）如图2，正比例函数y1=k1x（k1≠0）与反比例函数的图像相交于A、B两点，其中点A的横坐标为1。当时，x的取值范围是 。

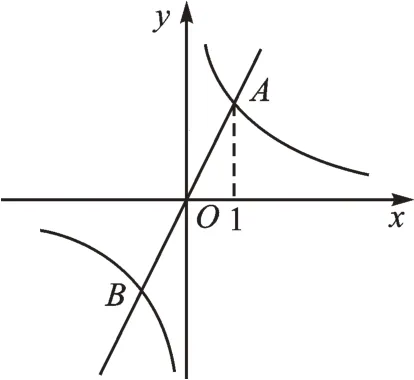
图2

【解析】因为正比例函数与反比例函数的图像均关于原点对称，点A的横坐标为1，所以点B的横坐标为-1。观察函数的图像，我们发现，当x＜-1或0＜x＜1 时，反比例函数图像在正比例函数图像的上方，所以当y1＜y2时，x的取值范围是x＜-1或0＜x＜1。

【点评】本题考查了正比例函数与反比例函数的基本性质，利用轴对称性推导出另一个交点B的横坐标，再利用函数图像的分布特点，分析得到满足条件的x的取值范围。

三、“源代码”升级

与函数有关的综合题，常常伴随着复杂的问题情境，这类题既考查同学们的审题能力，也考验同学们的逻辑思维和综合学力。

【升级重组】（2021•浙江金华）背景：点A在反比例函数的图像上，AB⊥x轴于点B，AC⊥y轴于点C，分别在射线AC、BO上取点D、E，使得四边形ABED为正方形。如图3，点A在第一象限内，当AC=4时，小李测得CD=3。

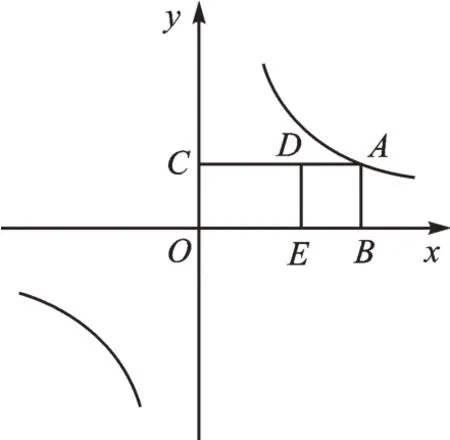
图3

探究：通过改变点A的位置，小李发现点D、A的横坐标之间存在函数关系。请帮助小李解决下列问题。

（1）求k的值。

（2）设点A、D的横坐标分别为x、z，将z关于x的函数称为“Z函数”。如图4，小李画出了x＞0时“Z函数”的图像。

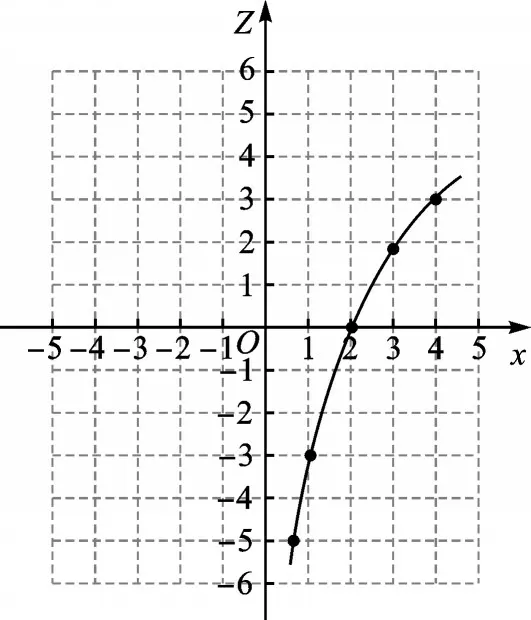
图4

①求这个“Z函数”的表达式；

②补画x＜0 时“Z函数”的图像，并写出这个函数的性质（两条即可）；

③过点（3，2）作一直线，与这个“Z函数”图像仅有一个交点，求该交点的横坐标。

【解析】（1）∵AC=4，CD=3，

∴AD=AC-CD=1。

∵四边形ABED是正方形，

∴AB=1。

∵AC⊥y轴，AB⊥x轴，

∴∠ACO=∠COB=∠OBA=90°，

∴四边形ABOC是矩形，

∴OB=AC=4，

∴A（4，1），

∴k=4。

（2）①由题意得A（x，x-z），

∴x（x-z）=4，

∴z=。

②图像如图5所示。

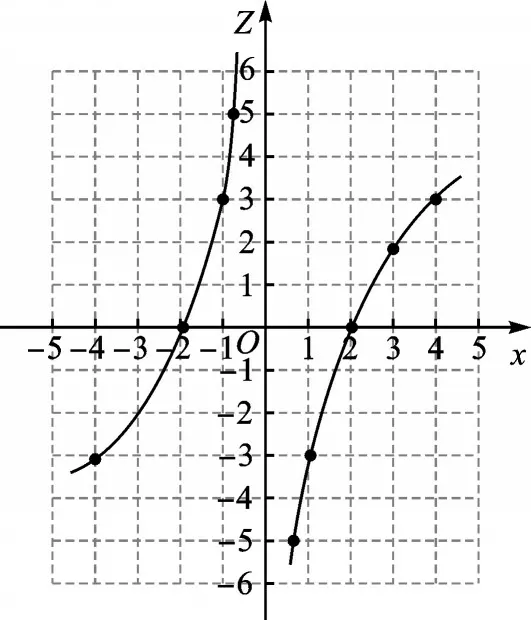
图5

性质1：x＞0 时，y随x的增大而增大；

性质2：图像是中心对称图形。

③设直线的表达式为z=kx+b。

把（3，2）代入，得2=3k+b，

∴b=2-3k，

∴直线的表达式为z=kx+2-3k。

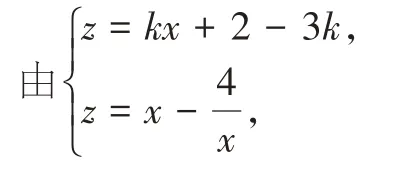
消去z，得（k-1）x2+（2-3k）x+4=0。

当k≠1，Δ=0时，

（2-3k）2-4（k-1）×4=0，

解得x1=x2=6；

当k=2时，

方程为x2-4x+4=0，

解得x1=x2=2。

当k=1时，

方程的解为x=4，符合题意。

另外，直线x=3，也符合题意，此时交点的横坐标为3。

综上所述，满足条件的交点的横坐标为2、3、4、6。

【点评】本题是反比例函数综合应用题，涉及的知识点较多，比如一次函数、二次函数、一元二次方程等。解题的关键是学会利用参数解决问题，学会把问题转化为方程组，再利用一元二次方程的根的判别式解决问题。