球形磨头单颗磨粒铣磨力模型与仿真研究

张景强，李明辉，宋鹏哲，王学智

沈阳航空航天大学机电工程学院

1 引言

航空航天领域许多具有复杂曲面或型腔的零件对表面质量有较高的要求，常采用铣磨加工方法完成加工。小尺寸球形磨头的铣磨加工方法为将尺寸较小的球形磨头夹持在多轴数控机床上，令磨头具有更高的运动自由度，实现形面复杂或加工空间有限的零件加工。当前对小尺寸砂轮和球形磨头的铣磨加工研究大多通过磨削实验进行，并着重研究铣磨参数对加工质量的影响[1-3]，对铣磨力和铣磨机理的研究偏少，尤其缺乏较为清晰的球形磨头铣磨力模型。

在研究磨削力模型时，由于磨削过程中磨粒数量多、几何形状复杂及切深不一致等原因，导致试验和观测磨削过程困难[4]。故常从单颗磨粒的角度分析磨削机理建立磨削力模型。文献[5]考虑了磨削过程中耕犁阶段对磨削力的影响，通过试验求出相关系数，建立了单颗磨粒磨削力模型。文献[6]以球形磨粒为例，结合麦钱特公式和布尔硬度测试实验，建立了磨削力模型。言兰等[4]通过划分材料变形区域建立磨削力学模型，并通过有限元仿真研究了磨削参数对磨削力的影响规律。杨军等[7]对磨粒的磨削过程进行理论分析，基于四种不同类型的磨粒建立了四种磨削力模型。这些磨削力模型对建立球形磨头铣磨力模型有借鉴意义，但不能直接应用。

本文通过分析球形磨头上单颗磨粒的铣磨加工过程，考虑磨头偏角对铣磨力的影响，结合有限元仿真实验求解相关系数，建立了磨粒的铣磨力模型，并通过仿真实验分析了铣磨参数对铣磨力的影响规律。研究结果为构建球形磨头铣磨力模型和选择铣磨加工参数提供了参考。

2 单颗磨粒的铣磨力模型

2.1 构建坐标系

图1为铣磨加工过程示意图。使用球形磨头进行铣磨加工时，磨头一边绕主轴旋转，一边做进给运动，磨头轴线与工件水平表面间存在一定的夹角。为分析磨头上磨粒在各方向的受力情况，构建磨头在各方向上铣磨分力的数学模型，建立O′-XYZ工件坐标系和O-FgtFgnFgf铣磨力坐标系。

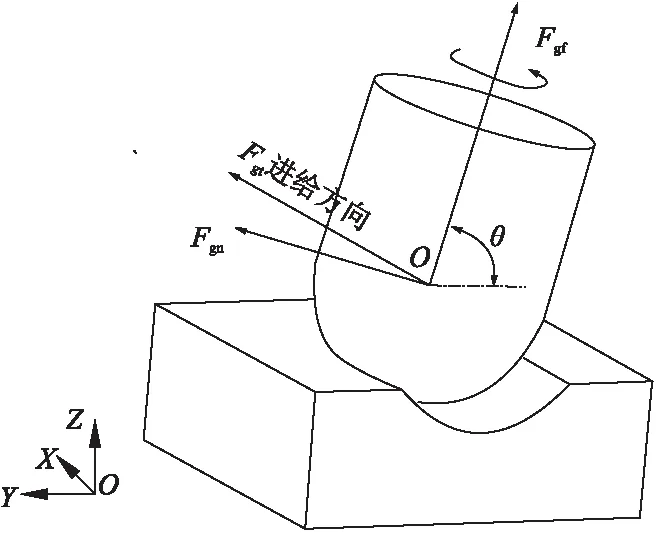
图1 铣磨加工过程

定义磨头在旋转轴方向上的力为轴向铣磨力Fgf，磨头进给方向定义为切向铣磨力Fgt。在工件坐标系中，X轴方向为磨头的进给方向，Z轴方向为工件水平表面的法线方向。磨头在X、Y、Z三个方向上的分力与铣磨力坐标系内各方向分力的关系可用磨头偏角θ表示为

(1)

2.2 单颗磨粒的几何模型

鉴于磨粒几何形状的复杂性，在研究磨削力模型时常将磨粒简化为规则几何形状，如球形[8]、圆锥形[9]、球头圆锥形[10]、切头方锥形[11]和规则多面体形[12]等。通过电镜观察CBN磨粒发现，CBN磨粒具有多个明显棱边，整体呈不规则的多面体形状(见图2)，因此将CBN磨粒近似为切头方锥形。

2.3 建立单颗磨粒铣磨力模型

(1)磨粒在磨头上的位置

由于磨头上磨粒位置各异，从单颗磨粒角度建立铣磨力模型时，需确定磨粒在磨头上的位置。本文以图3中磨头上K点处的磨粒为例建立铣磨力模型，当磨头以一定参数进行铣磨加工时，K点处磨粒的铣磨深度与磨头的铣磨深度相同，具有一定代表性。

(a)磨粒电镜形貌

(b)磨粒简化模型

图3 磨粒在磨头上位置

磨头半径为R，磨头与水平面之间的夹角为θ，磨头铣磨深度为ap。K点处的磨粒旋转半径为

r=Rcosθ

(2)

在Y-Y截面上，K点处磨粒的铣磨深度表示为

(3)

(2)磨粒在工件坐标系内的受力情况

构建磨粒铣磨力模型，在工件坐标系内对磨粒的铣磨过程进行受力分析，磨粒的受力状态见图4。

图4 磨粒铣磨过程受力分析

材料变形阻力Fg垂直于磨粒前表面与工件的接触区域S，Fg可在工件坐标系内分解为X轴方向分力Fx，Y轴方向分力Fy和Z轴方向分力Fz。材料变形阻力Fg可表示为

(4)

在工件坐标系内，各铣磨分力可表示为

(5)

式中，ψ为磨粒切向速度方向与进给方向的夹角。

(3)单位铣磨力模型

由式(5)可知，单位铣磨力可表示为

(6)

(7)

其中，平均磨屑厚度

(8)

式中，A，B和C均为系数，通过回归分析确定。

(4)最大未变形切屑厚度

式(6)中，最大未变形切屑厚度Agmax受各铣磨参数的影响，参照图3对磨屑的形成过程进行分析(见图5)。

图5 磨屑的形成过程

由图5可知，磨粒以速度Vs旋转，磨头以速度Vw进给，图中阴影部分为即将被切下的磨屑。s为转过相邻磨粒间隔时间内的磨头平移量，进给速度Vw与连续两次切削间隔时间乘积为

(9)

式中，λg为磨头上相邻磨粒间距。

最大未变形切屑厚度Agmax可表示为

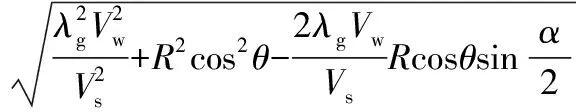
(10)

(11)

(5)单颗磨粒的铣磨力模型

结合式(1)、式(4)、式(7)、式(8)、式(10)和式(11)，在铣磨力坐标系内建立单颗磨粒的铣磨力模型，有

(12)

式中，Fg为铣磨合力；Fgt，Fgn，Fgf分别为切向、法向和轴向铣磨分力。

3 单颗磨粒的有限元仿真

3.1 有限元仿真模型

建立方锥形切头的磨粒模型，高为0.13mm，锥顶半角为-30°。工件为2mm×0.15mm×0.1 mm的长方体模型，磨头半径R为8mm。以磨粒旋转轴线为轴向铣磨力方向建立铣磨力坐标系。铣磨仿真时，工件位置固定，磨粒以一定的铣磨速度Vs沿轴线旋转完成从切入到切出的铣磨过程，旋转轴线与工件水平表面存在夹角θ，磨粒的铣磨轨迹如图6所示。

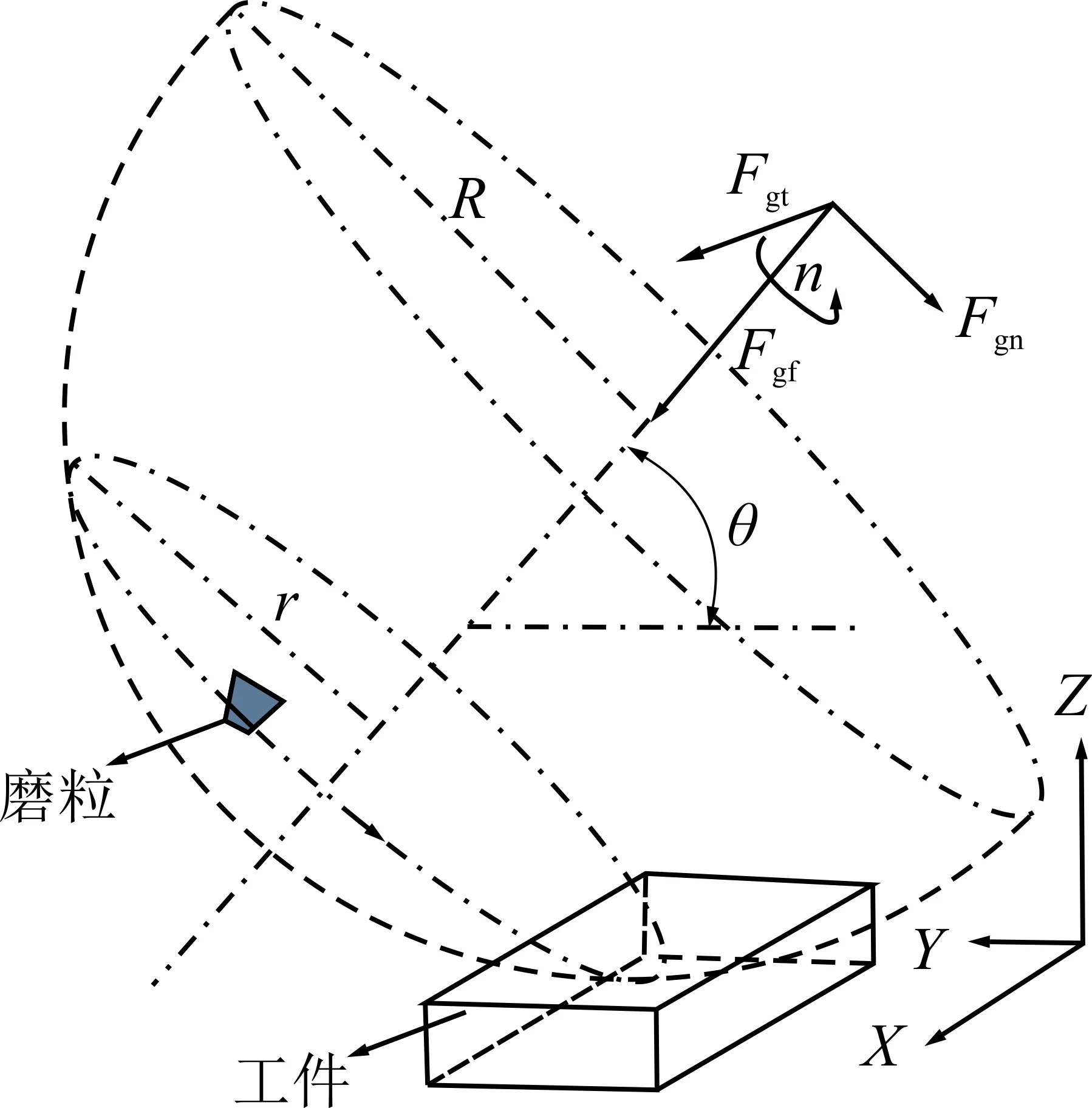
图6 仿真时磨粒的铣磨轨迹

为了提高仿真效率和准确性，在划分网格时对工件进行分区细化和密化处理，磨粒和工件的单元类型都定义为C3D8R。

3.2 材料模型与仿真方案

选取磨粒材料为超硬磨料立方氮化硼(CBN)，工件材料为TC4钛合金，两者的物理性能参数如表1所示。将磨粒设置为刚体，TC4材料的J-C本构模型参数见表2。

表1 CBN与TC4材料的物理性能

表2 TC4材料的J-C本构模型参数

采用单因素实验方法设计表3所示的实验方案，主要研究磨粒的铣磨速度、铣磨深度和磨头偏角对单颗磨粒铣磨过程中铣磨力的影响规律。

表3 铣磨仿真实验方案

4 单颗磨粒铣磨仿真结果与分析

4.1 磨粒铣磨过程

铣磨速度Vs=3.4m/s，磨头偏角θ=30°，铣磨深度ap=30μm 时，磨粒的铣磨过程见图7。图8为此铣磨参数下磨粒在各方向的铣磨分力曲线。

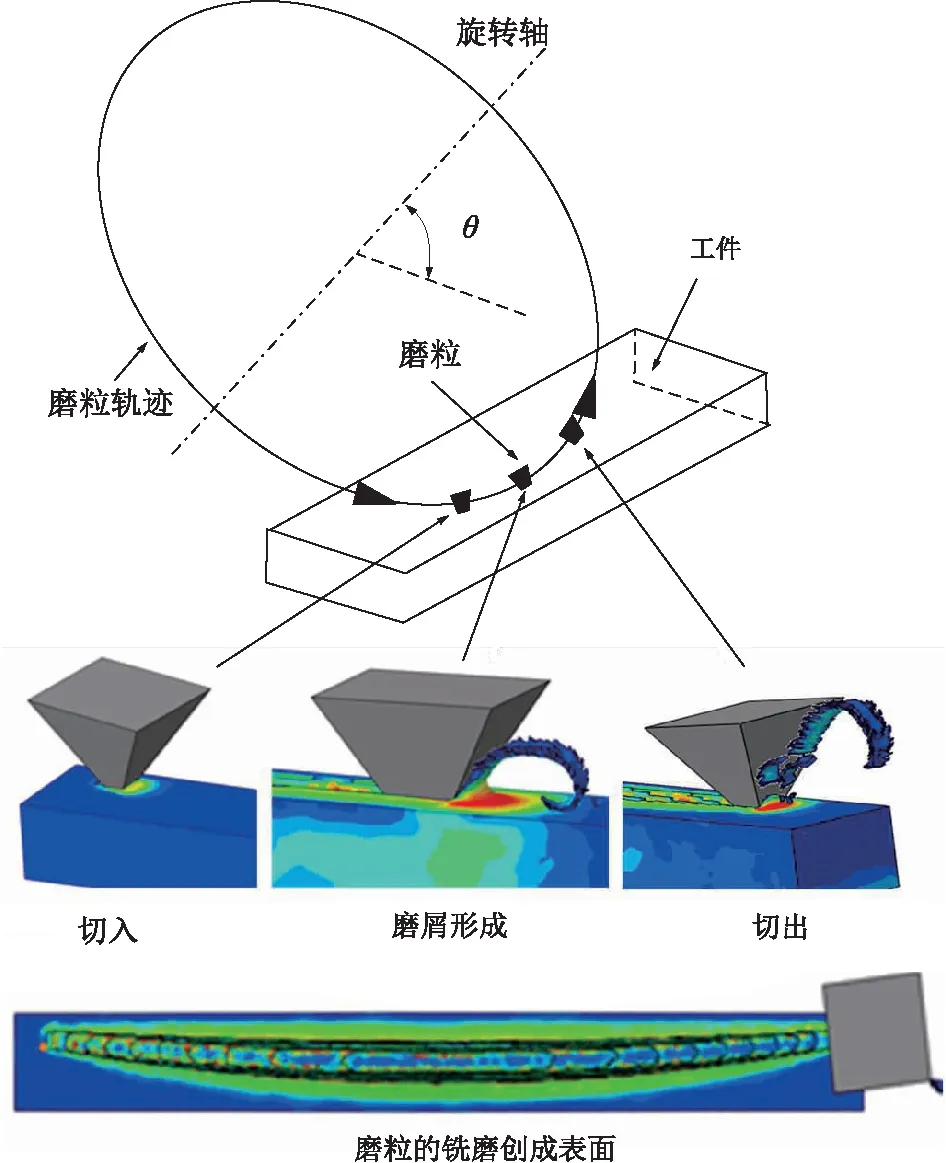
图7 单颗磨粒铣磨仿真过程

图8 磨粒铣磨力曲线

结合图7与图8得，随着磨粒的旋切，铣磨深度逐渐增大，各个方向的铣磨分力也随之增大。在铣磨深度达到最大值时，各方向的铣磨分力也达到最大值。随着磨粒继续旋切，铣磨深度开始减小，各方向的铣磨分力随之减小，直至磨粒切出工件，铣磨力减至零。

4.2 仿真得到的铣磨力与数学模型求解

在铣磨过程中，磨粒的铣磨深度先增大后减小，其产生的铣磨力也随之增大并减小。在一定铣磨参数下，取铣磨力最大值处的邻域平均值为该铣磨参数下的铣磨力值，此时磨粒旋转到最大铣磨深度位置处，各组铣磨仿真实验得到的铣磨力见表4。

表4 各组铣磨仿真的铣磨力

表5 铣磨参数下的平均磨屑厚度与单位铣磨力

结合式(7)，由线性回归分析求解系数，建立单位铣磨力Fp的数学模型为

根据单位铣磨力的数学模型，结合式(12)求解各铣磨参数下的铣磨力理论值(见表6)。

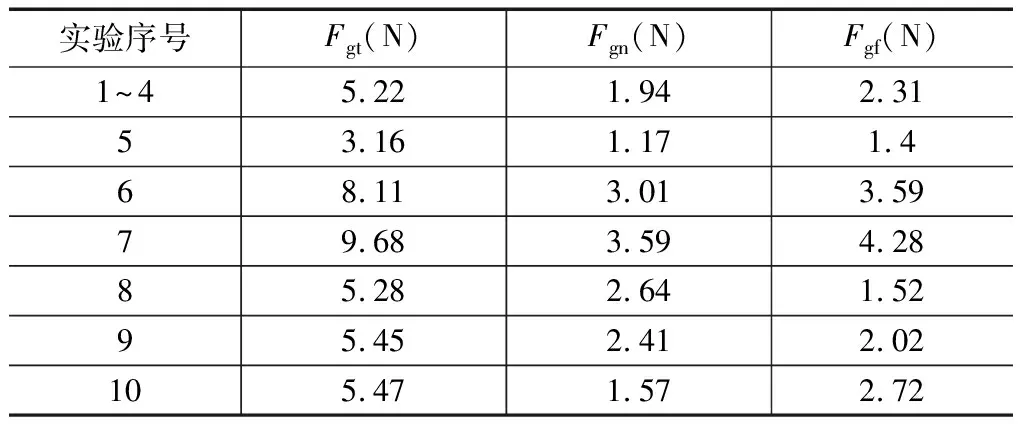
表6 铣磨力理论值

4.3 仿真与模型结果对比分析

在铣磨深度ap=30 μm，磨头偏角θ= 50°时，铣磨速度Vs对各铣磨分力的影响规律如图9所示。

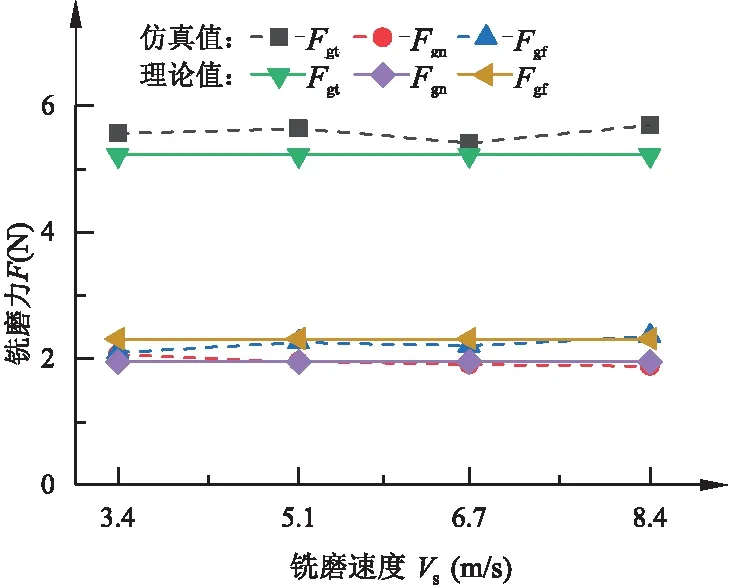
图9 铣磨速度对铣磨力的影响规律

由图可以看出，铣磨速度Vs从3.4m/s增大至8.4m/s时，各方向的铣磨分力基本保持不变。这是由于铣磨仿真时，磨粒在单次接触弧长范围内未沿进给方向进给，铣磨速度的增大(或减小)未能改变切屑厚度，对应的单位铣磨力未发生明显改变，因此铣磨力不变。由数学模型推导出的铣磨力理论值与仿真值平均误差为3.1%。

当铣磨速度Vs=5.1m/s，磨头偏角θ=50°时，铣磨深度ap对各铣磨分力的影响规律如图10所示。

图10 铣磨深度对铣磨力的影响规律

由图可得，各方向的铣磨力与铣磨深度之间存在明显的正相关性，铣磨深度越大，铣磨力越大。随着铣磨深度ap由20μm增至50μm，各向铣磨力呈现近似比例的线性增加，约增大2倍。这是由于铣磨深度增大时，磨屑厚度增大，铣磨力也会增大。铣磨力仿真值与理论值平均误差为6.8%。

当铣磨速度Vs= 5.1 m/s，铣磨深度ap=30μm时，磨头偏角θ对各铣磨分力的影响规律见图11。

由图11可知，在单次接触弧长内，磨头偏角的改变未对单颗磨粒的切向铣磨力产生影响，但对轴向铣磨力和法向铣磨力有明显影响。随着磨头偏角增大，法向铣磨力减小，轴向铣磨力增大，此变化规律与式(12)相符合。各铣磨分力理论值与仿真值的变化趋势吻合，数值平均误差为4.5%。

图11 磨头偏角对铣磨力的影响规律

5 结语

通过铣磨过程理论分析和有限元仿真实验建立了球形磨头上单颗磨粒的铣磨力数学模型，研究了铣磨参数对铣磨力的影响规律，得出以下结论。

(1)仿真结果表明，在磨粒的单次铣磨过程中，铣磨深度ap由20μm增至50μm的过程中，各向铣磨分力呈线性增加2倍。磨头偏角θ由30°增大至60°的过程中，磨粒的切向铣磨力基本保持不变，轴向铣磨力增大80%，法向铣磨力减小60%。在单次铣磨过程中，由于铣磨速度的变化未改变磨屑厚度，磨粒的各向铣磨分力基本保持不变。

(2)建立的球形磨头单颗磨粒铣磨力数学模型，其铣磨参数对铣磨力的影响规律和铣磨力数值与有限元仿真结果吻合度较高，在数值上两者的平均误差为 4.8%，且铣磨力变化规律相同，表明建立的单颗磨粒铣磨力数学模型准确。