利用扭摆实验探究简谐运动规律
周子栋,邵明珍,王才林,曾孝奇,张 欢
(南方科技大学 物理系,广东 深圳 518055)
简谐运动是一种常见的运动形式,广泛存在于诸多物理系统之中. 在大学物理实验课堂上,学生多基于单摆[1]或弹簧振子[2]实验验证简谐运动规律,实验类型有限. 为了拓展学生视野,达到融会贯通的教学目标,依据力学相似性[3]设计了一种新型扭摆实验. 与常见的扭摆实验[4-5]相比,本实验新增了智能手机和视频软件的运用,能够测量扭摆转角、角速度、角加速度和能量的时间演化曲线,进而验证简谐运动中的规律. 教学实践表明,本实验兼具趣味性和挑战性,有助于加深学生对简谐运动规律和力学相似性的理解,并提高学生数据分析、处理能力. 另外,本实验也丰富了物理实验与智能手机相结合的研究[6-10].
1 实验装置
本实验的扭摆装置主要包括铁架台、钢丝、刚体和智能手机,智能手机置于刚体下方,用来录制标记点转动视频,录像帧率为30 fps,如图1(a)所示. 铁架台的横杆中装有钻头夹,用来锁紧钢丝上端,如图1(b)所示. 刚体由悬架和若干个铁环组成,铁环放置在悬架上面. 悬架上的钻夹头用来锁紧钢丝下端,如图1(c)所示. 上下2个钻夹头之间所夹钢丝的直径和长度分别为(0.495±0.001) mm和(40.00±0.01) cm. 单个铁环的质量为(415.50±0.26) g,内径和外径分别为(80.10±0.06) mm和(109.98±0.10) mm,转动惯量为(961.4±1.4) kg·mm2.

图1 实验装置图
悬架的底部贴有轻薄纸片,纸片上有2个黑色标记点A和B,均位于悬架的轴线上,如图1(d)所示. 运用2个标记点连线的斜率来推算刚体转角.
2 实验原理
如图1(a)所示扭摆装置,上下钻夹头之间所夹钢丝的扭转系数为D,悬架上铁环的数目为n,
铁环的总转动惯量为In,悬架的转动惯量为Ix.当刚体转离平衡位置的转角为θ时,钢丝因扭转形变而产生恢复力矩,其大小为Dθ,方向与刚体转动方向相反.当阻尼作用可忽略不计时,刚体仅受恢复力矩作用,其转动方程为[4-5]
(1)
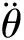
θ=Qsin (ωt+φ),
(2)
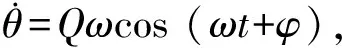
(3)
(4)
其中,Q和φ分别表示刚体转动的幅度和初始相位.ω表示转动角频率,依赖于钢丝的扭转系数和刚体的转动惯量,函数关系为
(5)
在式(1)等号两侧对转角积分,可得
Ek=-Ep+E,
(6)
其中Ek,Ep和E分别称为扭摆的动能、势能和机械能.由式(6)可知,扭摆在转动过程中机械能守恒.Ep和Ek分别为
(7)
(8)
将式(2)和式(3)分别代入式(7)和式(8),并结合式(5),可得
(9)
(10)
由此可见,当势能达到极小值时,动能达到极大值;反之,当势能达到极大值时,动能达到极小值.另外,势能和动能的演化频率是2ω,是转角演化频率的2倍.
3 实验方法
探究上述实验原理中的的简谐运动规律,关键在于追踪刚体转角的时间演化.为此,可在悬架的轴线上制作2个标记点A和B,如图1(d)所示,然后根据两点连线斜率推算出转角为
(11)
其中,(xA,yA)和(xB,yB)分别为标记点A和B的坐标.由于刚体在转动的同时存在小幅度摆动,为了减小其摆动幅度,应该待刚体静止后再旋转上方钻夹头来扭转钢丝带动刚体转动.另外,上述算法能够使2个标记点的摆动成分相抵消减小实验误差.
目前,有多款视频软件可以提取标记点的坐标数据,如Tracker[11-12],Capstone[13]和Matlab[14]等. 以Tracker为例,简述坐标演化数据的提取方法. Tracker界面如图2所示,其操作步骤为打开视频文件、剪辑设定、定标、坐标轴设定、轨迹创建和自动追踪等. 在Tracker提取出坐标演化数据后,将数据拷贝到Origin软件,运用反正切函数计算转角θ. 由于Origin软件中的反正切函数值域是(-90°,90°),为了便于数据处理,建议在录像时控制扭摆转动幅度并调整手机位置,使标记点运动限于Tracker界面中的第一、四象限或第二、三象限.

图2 Tracker界面
得到转角后,通过差分法估算角速度
(12)
其中,θ(t)和θ(t′)分别为t时刻和t′(t′>t)时刻的转角.式(12)等号右边分式具有平均角速度的含义,在t′-t极小时用于估算(t+t′)/2时刻的瞬时角速度.同理,可运用差分法估算角加速度
(13)
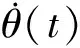
4 实验结果
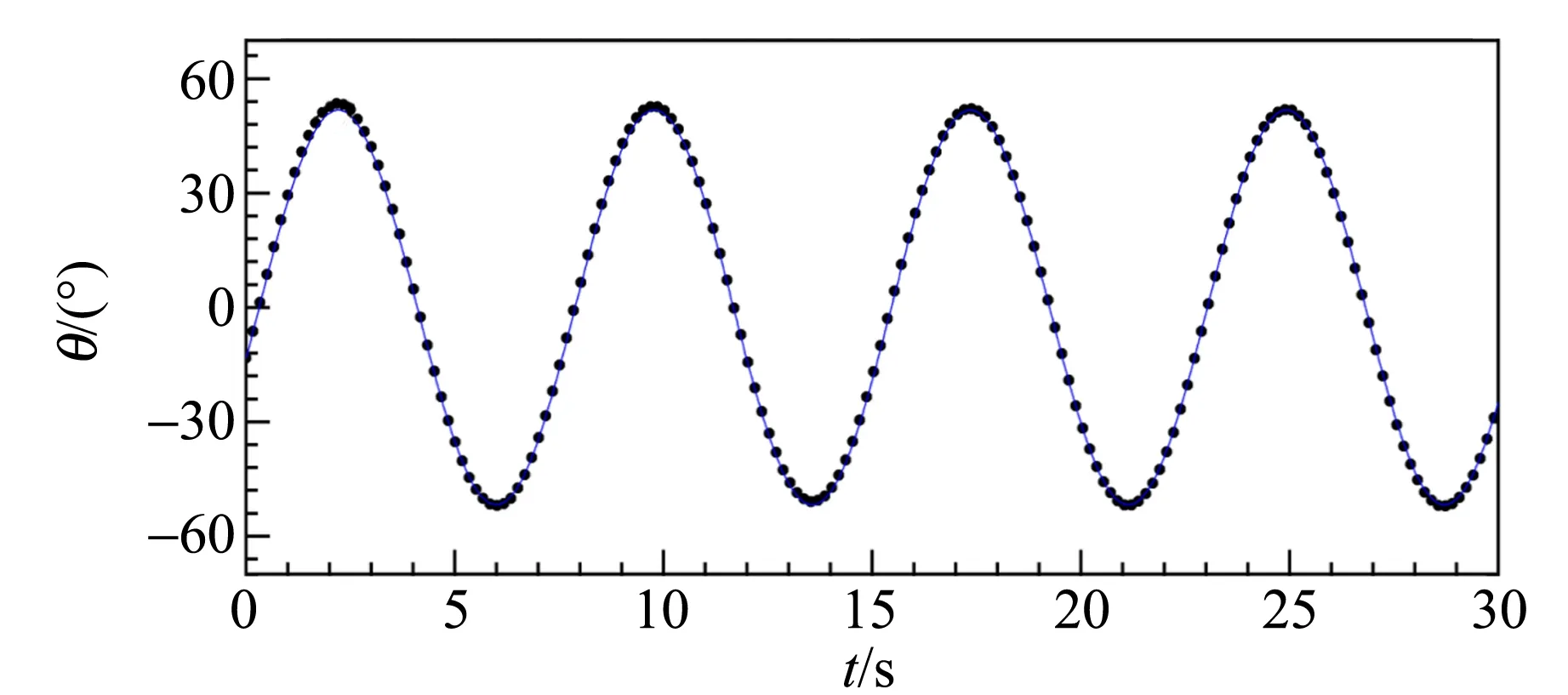
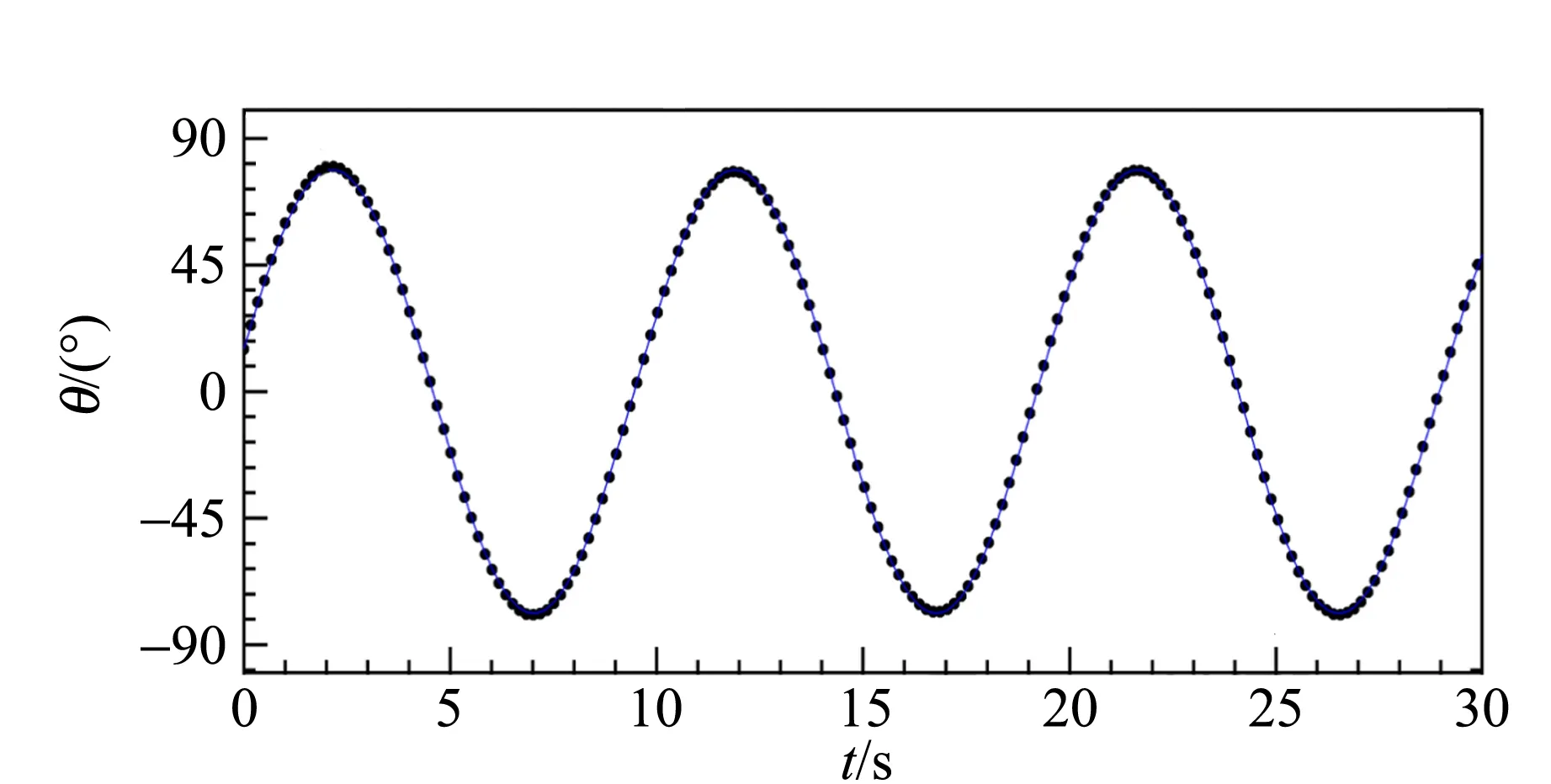
刚体转角θ随时间的演化曲线,以及铁环数目n对曲线的影响,如图3所示.转角演化具有周期特征,转动幅度在约30 s的时间窗口内衰减较小,而且转动频率随着铁环数目的增加而减小. 图3中蓝色实线表示拟合曲线,目标函数为式(2),拟合结果见表1.

(a)n=0
(b)n=1
(c)n=2
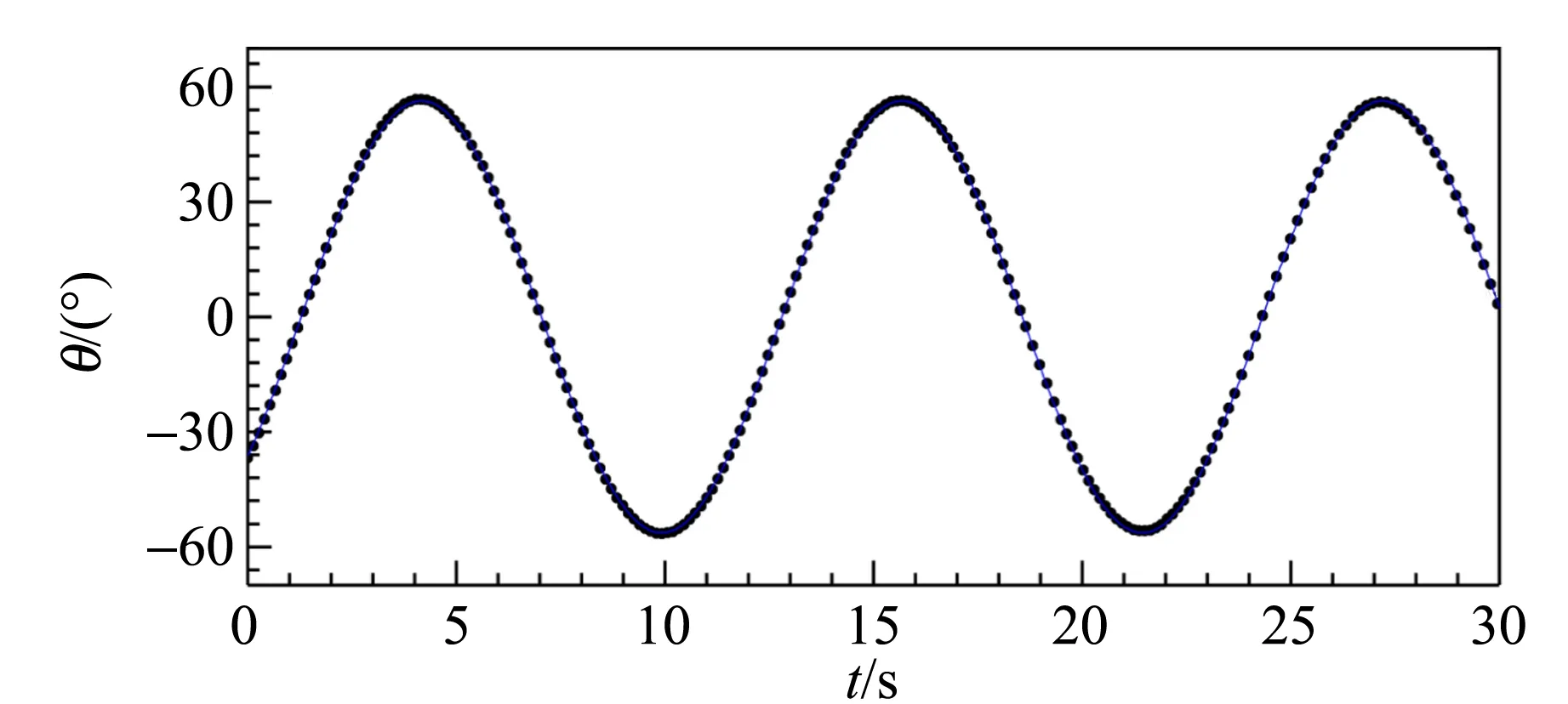
(d)n=3图3 不同铁环数目下刚体转角的时间演化散点图
拟合结果说明,实验数据和拟合曲线符合得较好,可近似认为刚体在做简谐运动. 需要指出的是,由于实验数据的时间分辨率约为33.3 ms,为了使数据点容易辨认,图中仅显示了25%的数据.

表1 不同铁环数目下刚体转角演化数据的拟合结果
基于表1中的拟合结果,可以探索刚体转动角频率ω和铁环总转动惯量In之间的关系,实验结果如图4所示.图4中蓝色实线表示拟合曲线,拟合目标函数采用式(5).从图4中可以看出,实验数据同理论曲线符合得较好,进一步验证了简谐运动规律.另外,经过拟合得到了钢丝的扭转系数和悬架的转动惯量,结果分别为D=(1.007 9±0.001 4)×10-3J和Ix=(0.506 2±0.000 8)×10-3kg·m2.
最后,基于转角演化数据,并采用差分法,可以得到角速度和角加速度随时间的演化曲线. 然后,将转角和角速度分别带入式(7)和式(8),并结合D和Ix的拟合结果,可以得到势能和动能的演化曲线. 图5展示了铁环数目n=1时,扭摆转角、角速度、角加速度、势能、动能和机械能的时间演化散点图. 转角与角速度之间的演化相位差约为π/2,而与角加速度之间的演化相位差约为π;势能和动能的演化呈现出此消彼长的关系,而且演化速度较快;在此过程中机械能基本保持不变. 上述特征验证了理论预期. 另外,由于转角测量存在误差,而在运用差分法计算角速度时该误差会放大,所以图5(b)中出现了明显的噪音. 该噪音在图5(c)中更加明显,因为角加速度的计算涉及了2次差分.
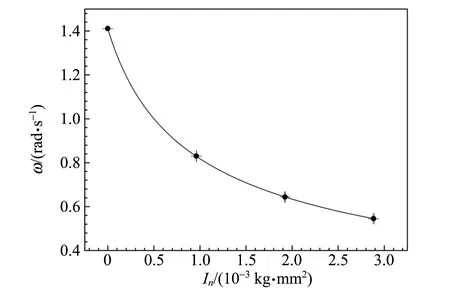
图4 转动角频率和铁环总转动惯量的关系图
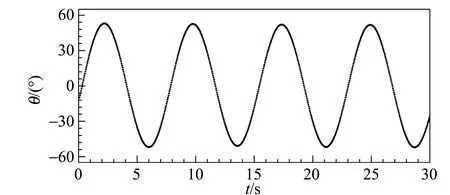
(a)
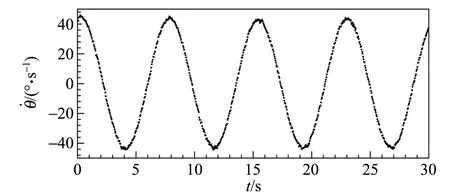
(b)

(c)

(d)图5 扭摆各物理量随时间演化散点图
5 结束语
设计了扭摆实验用来引导学生从扭摆的角度探究简谐运动的基本规律. 通过运用智能手机和视频软件,学生可以测量扭摆中多个物理量随时间的演化曲线,进而验证理论预期. 教学实践表明,本实验有助于拓展学生视野,加深学生对简谐运动和力学相似性的理解,并锻炼学生的数据分析及处理能力.

