利用激光三角法测量钢丝的弹性模量
郑雪丽,邱 丽,汪 涛,李巧梅,杨骏骏
(重庆大学 物理学院 物理国家级实验教学示范中心,重庆 401331)
弹性模量是材料的固有属性,其大小能够表征材料抵抗形变的能力[1],是工程选材时须考虑的重要参量,因此准确测量弹性模量对工业生产具有重要意义. 弹性模量测量实验是各高校大学物理课程中必做的实验,其测量关键点是精确测量被测材料的微小形变量. 本文基于弹性模量测量特点,结合光电子技术,采用激光三角法测量钢丝的弹性模量.
1 实验原理
1.1 激光三角测量法
采用激光三角测量法测距是短距离激光测距中常用的方法,根据激光照射角度不同可以分为直射式激光三角法和斜射式激光三角法[2-3]. 本文采用斜射式激光三角法测量弹性模量,其光路如图1所示,光路符合沙姆定律[4],即物平面(物体移动的平面)、聚焦透镜平面和像平面三者交于1条直线. 激光三角法测量微小位移时,激光照射到被测物上产生漫反射,反射光经凸透镜成像被PSD位置传感器接收,当物体移动时,成像光斑也会随着相应位移发生移动,根据PSD测距原理可以计算出像点位移,再根据几何关系即可计算出待测物的位移. 根据图1中的几何关系,光斑位移为
(1)
其中,Δx为像点在PSD上的位移,a为物距,b为像距,θ为物法线与聚焦透镜光轴的夹角,φ为PSD光敏面与光轴的夹角.
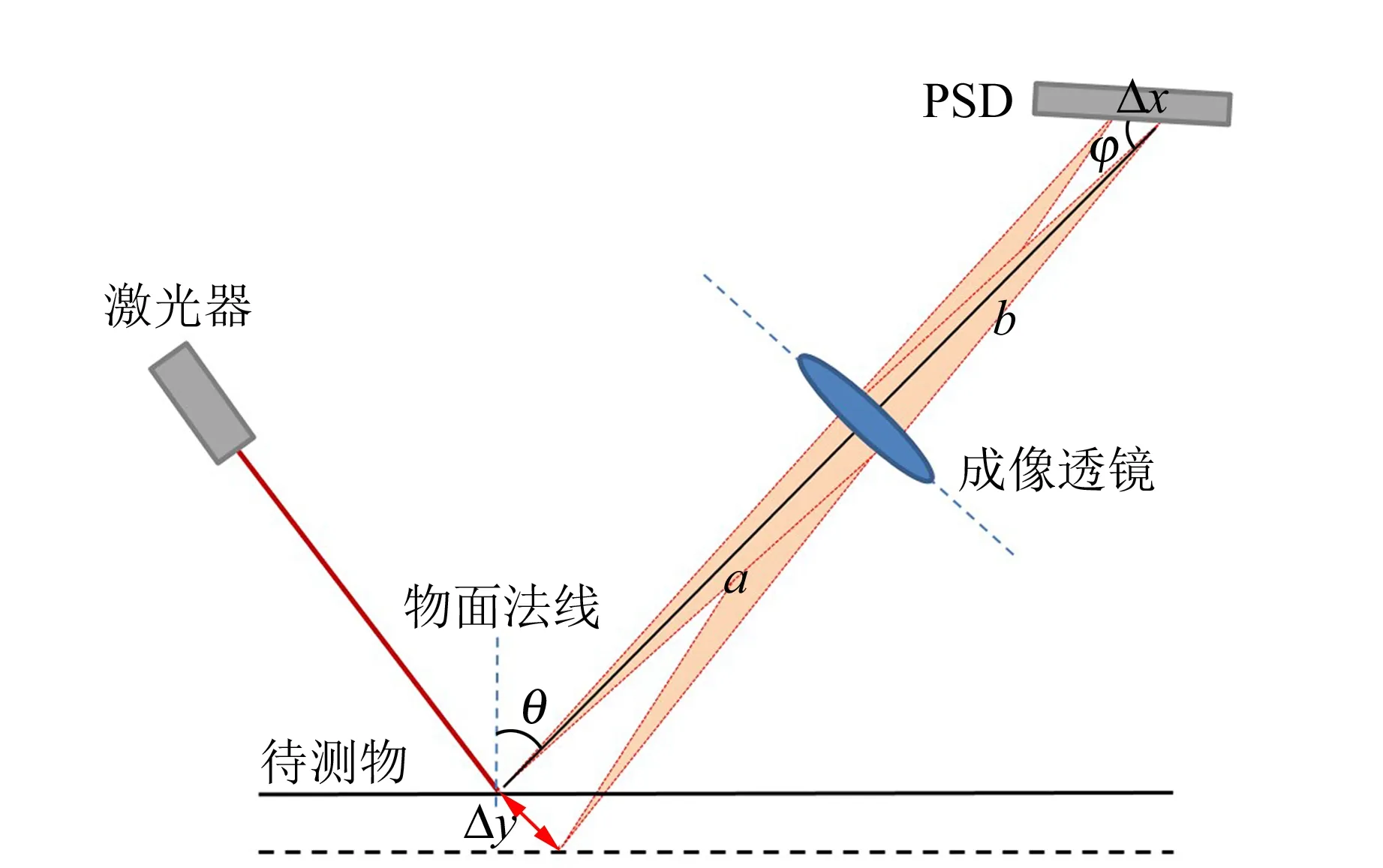
图1 斜射式激光三角法光路图
1.2 系统结构和原理
采用斜射式激光三角法测量弹性模量的整体结构如图2所示. 摆放光路时,要求柱形夹具的法线、成像透镜平面、PSD接收的像平面交于1条直线,以遵循沙姆定律. 在柱形夹具上贴磨砂纸片,激光照射到纸片上,产生漫反射,反射光经过凸透镜后在PSD位置接收传感器上成像. 当在弹性模量测量仪上加载荷时,柱形夹具随钢丝伸长而向下移动,像点也会随之有相同的位移量. 根据胡克定律,弹性模量为
(2)
其中,F为施加在钢丝上的力,S为钢丝横截面积,L为钢丝的有效长度,ΔL为在施加载荷后钢丝的伸长量.通过几何关系可知
(3)
将式(3)代入式(2),可得钢丝的弹性模量为
(4)
因此,只要测出式(4)中的相关参量即可计算出钢丝的弹性模量.

图2 测量弹性模量的结构图
PSD位置传感器是对入射光位置敏感的PIN型光敏二极管,分为P层、I层和N层,其结构如图3(a)所示. 当光照射到光敏面时会在下表面形成光电子,光电子通过均匀分布的P型电阻层被电极收集. 以PSD集合中心为坐标原点,在PIN位置传感器上加反偏电压V,由于入射光点和输出电极1和2之间存在电动势,则光电子形成的光电流I1和I2通过PIN位置传感器分别流向电极1和2,如图3(b)所示,其大小与入射光点和电极间距成反比[5],即
(5)
其中R1,R2分别为入射光点与电极1和电极2之间的等效电阻,h为PSD器件长度的1/2,x为入射光点到PSD几何中心的距离.根据式(5)得
(6)
因此,入射光点到PSD几何中心的距离可直接通过探测光电流来确定,而与表面上的光斑强度、分布、对称性和尺寸无关[3].

(a) 一维结构图
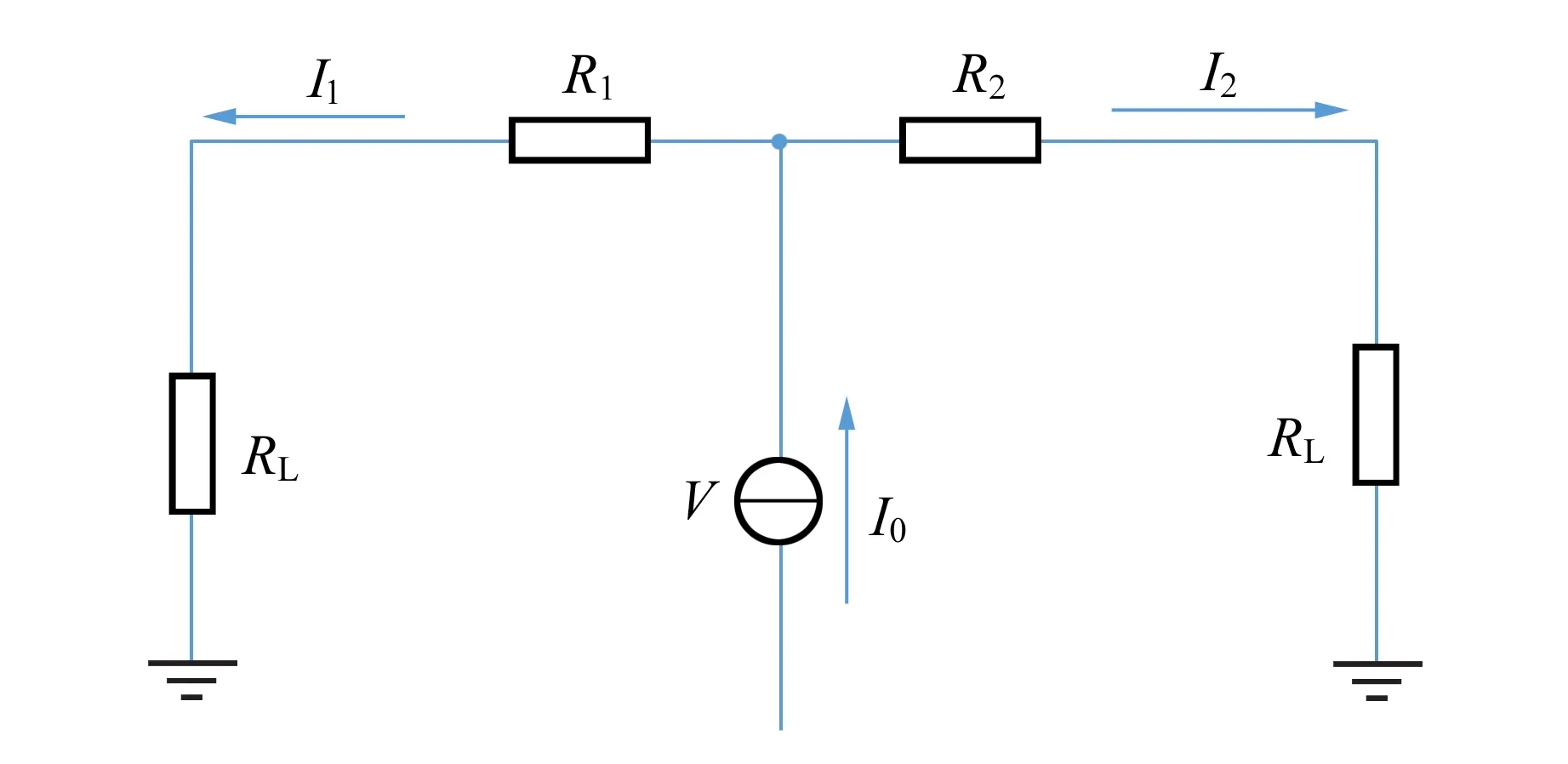
(b)等效电路图3 PSD的一维结构图和等效电路
选用型号为DRX-1DPSD-0A03-15的PSD器件,其有效光敏面为1 mm×15 mm,采用具有高精度、高线性度、位置连续变化等优点的双电源(±12 V)进行供电. 外电路采用运算放大器(OPA4101NJ)对PSD输出的微小电流信号进行I-V放大及运算处理,其电路框图如图4所示.
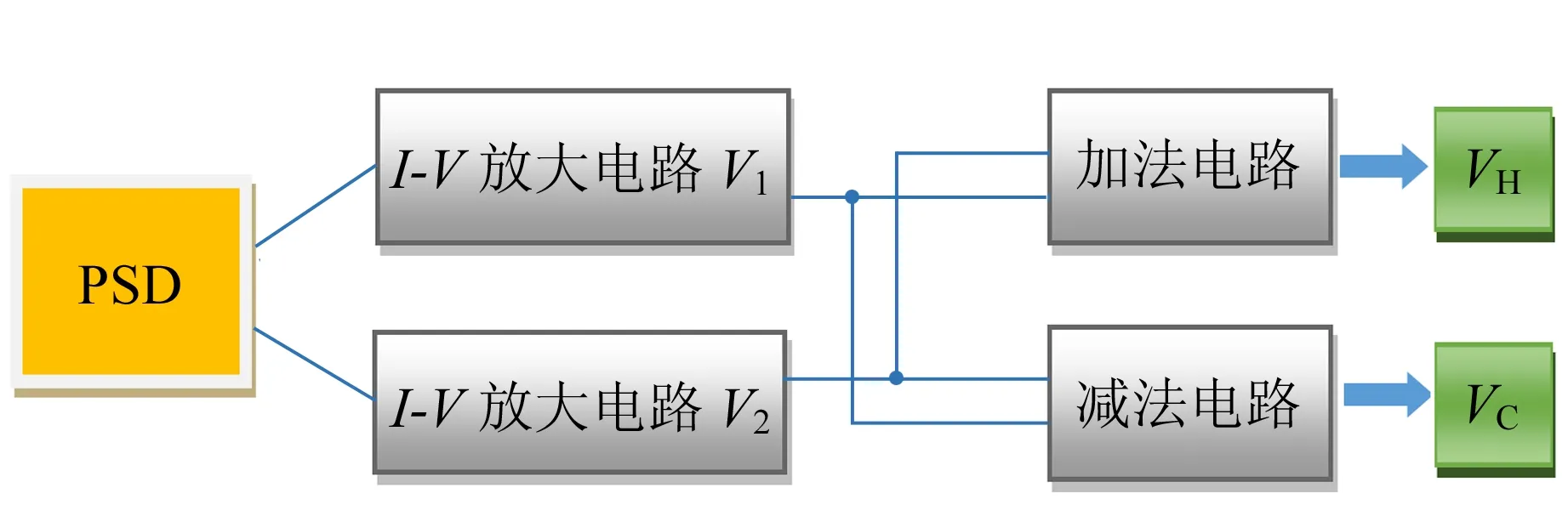
图4 PSD电路框图
将I1和I2转换为V1和V2,经加法电路和减法电路输出为V1+V2和V1-V2,其大小可用万用表分别测出.为叙述方便,分别用VH和VC表示V1+V2,V1-V2,则式(6)可改写为
(7)
光点在PSD器件上的位移为光点移动前后偏离PSD器件中心的距离之差,其表达式为
(8)
2 实验测量与数据处理
2.1 实验测量
在实验教学中,选用光敏面长度为15 mm的PSD,并选用直径d=0.796 mm,有效长度l=760.0 mm的钢丝作为待测材料. 采用斜射式激光三角法测量其弹性模量的步骤为:
1) 打开弹性模量测量仪系统电源,调节系统,使施加在钢丝上的载荷为2.000 kg;
2) 选用焦距f=100 mm的聚焦凸透镜,打开激光器,按图2所示调节光路;
3) 调节光路时,使物距等于像距,即a=b=200 mm;
4) 打开PSD电源和万用表,将钢丝上载荷从2.000 kg增加到17.000 kg,用万用表测量并记录输出电压VH,VC;
5) 将钢丝上的载荷从17.000 kg减少到2.000 kg,用万用表记录输出电压VH,VC.
2.2 数据处理
测量数据如表1所示.
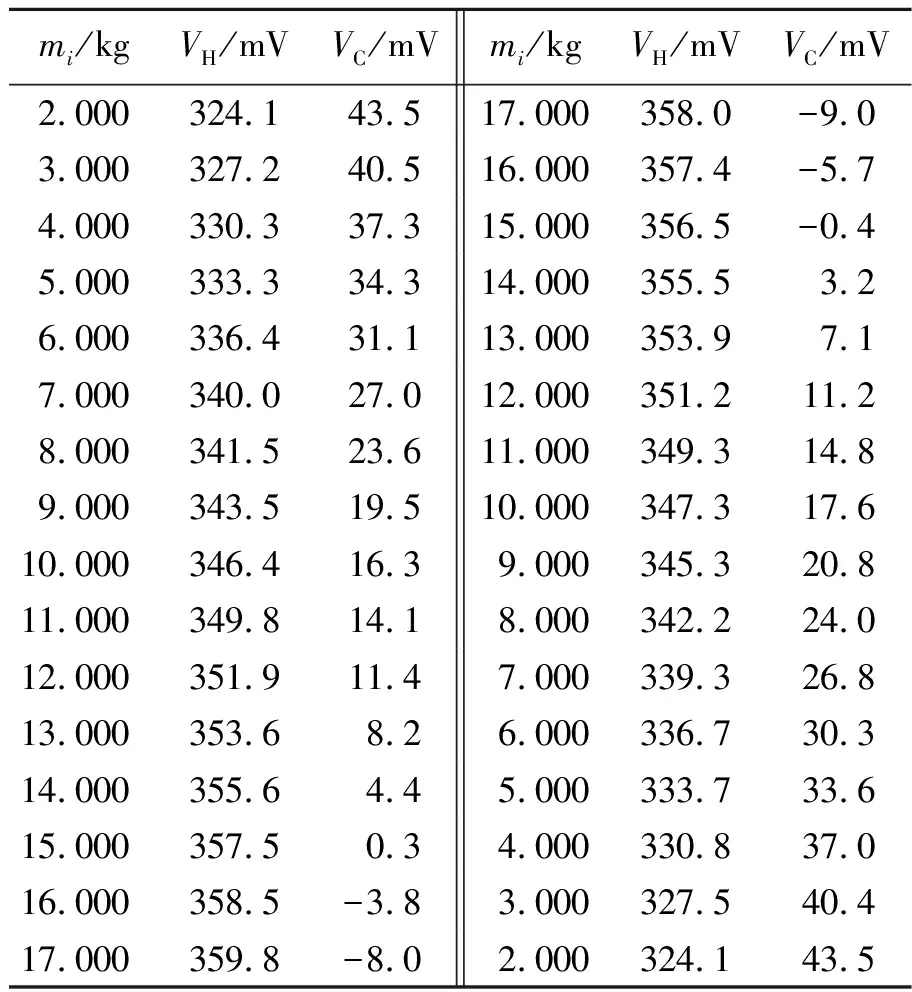
表1 测量数据记录表
根据表1进行数据处理,处理要求为:
1)采用最小二乘法计算每加1.000 kg载荷,钢丝的伸长量;
2)计算弹性模量的不确定度;
3)与标准值比较求出相对偏差.
下面以1组测量数据为例介绍数据处理方法和过程.
在实验光路满足沙姆定律的条件下,调整PSD接收平面,使其与被测平面平行.根据图1中的几何关系可知φ+θ=90°,则sinφ=cosθ,代入式(3)可得
(9)
调节光路,使物距等于像距,即a=b,则弹性模量可表示为
(10)
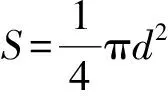
(11)
根据表1中载荷相同的VH,VC的2次测量值,分别求其平均值,并代入式(8)计算出增加不同质量的载荷时,光斑在PSD器件上的位移量Δx,再利用最小二乘法拟合得到Δx-m曲线,如图5所示.拟合得到的斜率代入式(11)计算得到钢丝的弹性模量E=(1.94±0.04)×1011N/m2,Er=3.5%.
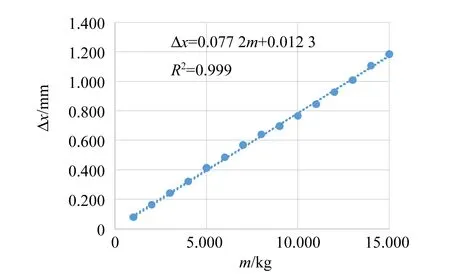
图5 Δx-m线性拟合图
3 结果分析
对比斜射式激光三角法和光杠杆法测量数据的相对偏差,如图6所示. 从图中可知,斜射式激光三角法测量数据的稳定性更高、误差更小. 其误差的可能来源有:
1)在钢丝伸长过程中,物像各点可能没有严格满足物像关系;
2)由于凸透镜放置的位置、角度不够精确,导致像在移动时,其中心位置和PSD的中心没有完全重合;
3)透镜成像畸变;
4)钢丝直径和有效长度的测量误差;
5)测量实验装置中的光源、载荷、夹具的稳定性不够;
6)背景光的影响.
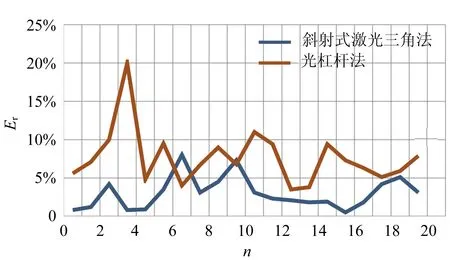
图6 斜射式激光三角法和光杠杆法测量相对偏差对比图
4 结束语
斜射式激光三角法测量弹性模量是将现代技术与经典实验相结合,具有光路简单、精度高、稳定性好等优点,适用于普通物理实验课. 另外,该方法为非接触式测量,除用于本实验外还可以用于热膨胀测量、厚度测量、热形变等实验中. 将激光三角法用于其他测量实验,可以拓宽学生的视野,提高实验的综合性和现代性.

