轨道缺陷图像检测算法的优化

闵 锐,黄楚云,张晓峻,孙晶华

(1.湖北工业大学 理学院，湖北 武汉 430068；2.哈尔滨工程大学 物理与光电工程学院，黑龙江 哈尔滨 150001)

中国铁路建设规模的扩大，对铁轨的工作要求变得更加严格. 考虑到铁路安全问题和隐患处理的重要性，需要定期对轨道进行探伤和状态检测，以掌握高质量的轨道状态数据，保证轨道的正常使用[1]. 采集轨道状态信息并及时处理是轨道维护的关键环节[2]，常规轨道检测方法虽然灵敏性和损伤检出率较高，但其工作成本和对人工的要求很高.

利用数字图像处理技术进行轨道状态检测的方法为轨道无损检测的发展和轨道探伤提供了新思路. 例如，将背景差分法应用于缺陷图像分割，通过自适应阈值分割和滤波方式去除噪声点对缺陷识别的干扰，提高钢轨缺陷的检测率[3]；基于机器视觉技术设计钢轨表面缺陷检测算法，对钢轨表面区域提取算法进行优化，提高了检出率，但算法的误检率未能得到良好地控制[4]；利用图像灰度梯度特征进行平滑滤波，通过差分分割实现钢轨表面缺陷检测的目的，有效弱化了光源和钢轨表面因素的影响[5]；基于机器视觉和卷积神经网络提出轨道表面缺陷检测方法，利用形态学滤波与概率霍夫变换算法去除原始图像中的噪声，通过Canny算法实现轨道表面缺陷的自动提取[6].

上述的轨道图像检测方法中，图像降噪预处理和缺陷边缘检测是最关键的步骤. 针对图像降噪问题，BM3D算法是目前去噪效果最好的算法之一[7]；针对受白噪声影响的阶跃型边缘检测问题，Canny算法的检测效果较好[8]. 但这2种算法运行时间比较长，不能满足实时性要求. 本文基于OpenCV软件平台采用C++语言编写算法，开展轨道缺陷检测算法的优化研究.

1 BM3D算法

针对轨道图像噪声严重、缺陷边缘模糊等问题，通过图像降噪预处理算法进行改善，为后续的缺陷检测提供良好的基础. BM3D算法可以很好地实现图像的滤波处理，该算法包括基础估计和最终估计2个步骤，这2个步骤中又各自包含相似块分组、协同滤波和聚合3部分[9]，算法流程图如图1所示.

(1)

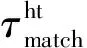
图1 BM3D算法流程

对得到的矩阵进行三维变换，将矩阵中小于设定参量的值设为0.对非零成分数量进行统计，再对其进行三维逆变换处理，得到基础估计的三维矩阵为

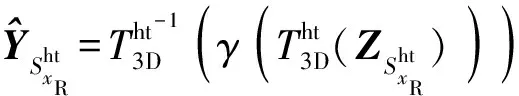
(2)

把逆变换后的图块对应到原来的位置，通过统计非零成分数量进行权重分配，利用叠放的图块及每处权重的比值即可去除图像中的大部分噪声点，得到基础估计图像为

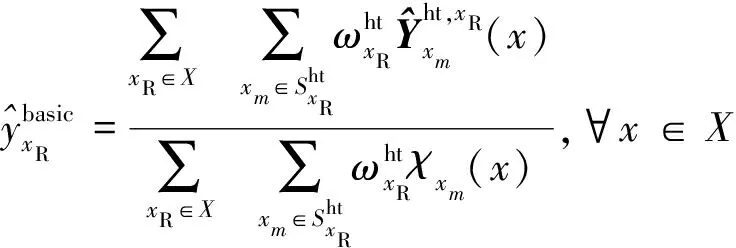
(3)

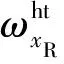
第二步，最终估计.利用基础估计中相同的分组方法，将基础估计图块再次进行块匹配，堆叠成新的相似图块集合，表示为

(4)

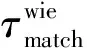
对含噪图像块和基础估计图块堆叠形成的2个三维矩阵分别进行三维变换，利用基础估计图块的变换系数，采用经验维纳滤波对原始含噪图像进行处理，得到估计权重，并进行三维逆变换.

(5)

经过加权平均变换后，得到最终的估计图像，会包含更多的图像细节.

2 BM3D算法优化

由于BM3D算法复杂度较高，为了拓展其实用性，本文对该算法流程进行改进，以达到高效处理的目的.

2.1 BM2D+1D算法

BM3D算法是将寻找到的相似图块进行二维变换后用欧氏距离测量其相似程度，然后叠成三维数组. 此时得到的图块已经进行了二维变换处理，只需再加上1次一维变换即可代替直接进行的三维变换. 同时三维变换采用可分离的正交变换，分解为各个相似块自身的二维变换以及相似块之间的一维变换，便于后续计算直接复用二维变换结果. 将BM3D算法转变为BM2D+1D算法，既可以保证算法运行结果的高质量，又能提高算法的运行速度，算法流程图如图2所示.

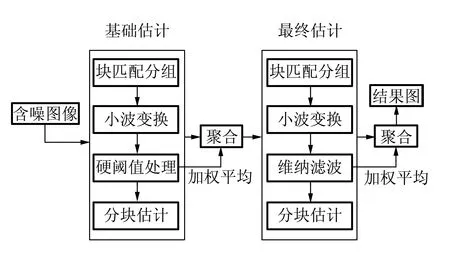
图2 BM2D+1D算法流程

为更好地捕捉图块中的周期性信息，图像块的二维变换采用离散余弦变换，由此得到所有相似块的二维变换系数. 再利用小波变换对二维变换的结果进行一维变换，实现图像块的三维变换，进一步降低算法的复杂度，一维离散小波变换[12]表示为

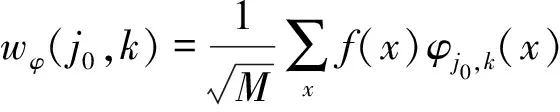
(6)

(7)

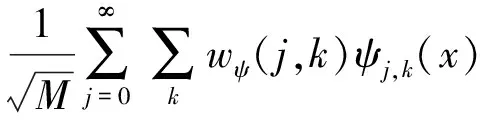
(8)

其中，wφ(j0,k)和wψ(j,k)为近似系数和小波函数，φj0,k(x)和ψj,k(x)为不同尺度和不同位置的小波函数，k为位置偏移量，j为尺度阶数.

优化后的算法保留了原算法的去噪框架，利用可分离的二维离散余弦变换和一维离散小波变换对图像块进行滤波处理，其他处理方法不变，在保证处理效果的同时提升了处理速度.并且在块匹配分组过程中将3×3图块窗口放大到6×6窗口，减少参考块的数量，加快相似块的处理速度.

2.2 仿真实验

为了减少运算量，提高检测效率，在对轨道图像检测前，先进行感兴趣区域提取，截取含有缺陷的区域，得到带有缺陷的轨道图像，大小为159×159 pixel. 为了降低算法的复杂程度，并便于图像二值化处理，将输入图像转变为灰度图像，如图3所示. 向图像中分别加入单一高斯噪声(噪声方差δ=40)和高斯噪声与椒盐噪声的混合噪声(高斯噪声方差δ=40、椒盐噪声像素点d=800)，得到模拟含噪图像,如图4(a)和图5(a)所示.

利用中值滤波、高斯滤波、维纳滤波、BM3D算法和本文提出的BM2D+1D算法分别对高斯噪声图像和混合噪声图像进行处理(实验所用计算机CPU为i7-9750H，内存为16G)，处理结果如图4和图5所示.

图3 原图

(a)高斯噪声图像 (b)中值滤波

(c)高斯滤波 (d)维纳滤波

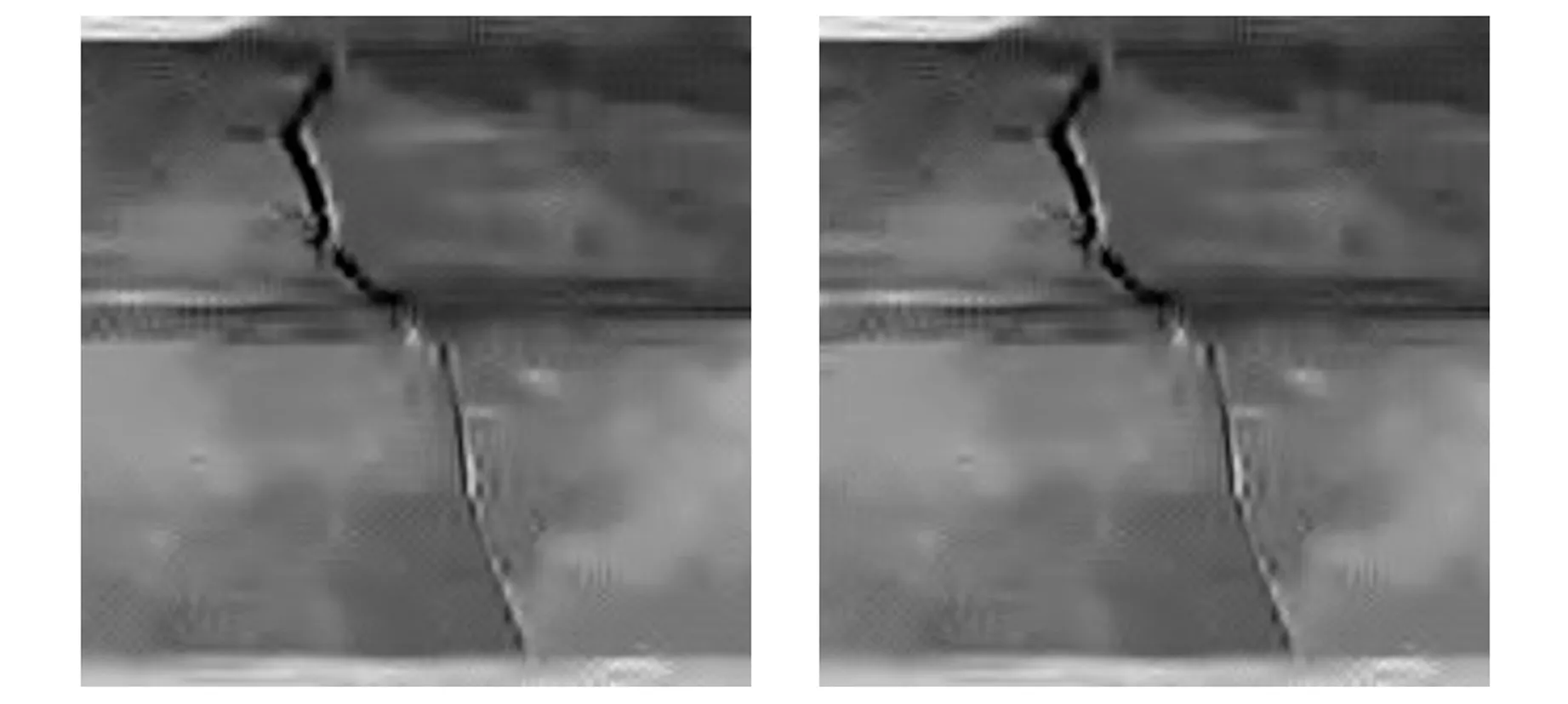
(e)BM3D (f)BM2D+1D图4 高斯噪声去噪

(a)混合噪声图像 (b)中值滤波

(c)高斯滤波 (d)维纳滤波

(e)BM3D (f)BM2D+1D 图5 混合噪声去噪

在单一高斯噪声图像处理中，从视觉效果上看，5种去噪算法都对高斯噪声图像带来了一定程度的平滑模糊. 但中值滤波、高斯滤波和维纳滤波方法不能完全去除高斯噪声，而BM3D算法和BM2D+1D算法能有效去除高斯噪声.

对于混合噪声图像的处理，由于在模块匹配步骤中受到了其他类型噪声的干扰，导致BM3D算法块匹配不准确，使得最终去噪结果失真. 可以看出，BM3D算法仅对含单一高斯噪声图像的去噪效果较好，且须在不受到其他噪声干扰的情况下进行. 而BM2D+1D算法因为加入了一维离散小波变换，因此不易受到其他噪声干扰，可以更加精准地识别图像噪声点.

在图像质量评价中，峰值信噪比(RPSNR)值越大说明去噪算法效果越好. 对图4和图5所示的5种去噪算法运行结果进行对比，RPSNR值结果如表1所示. 由RPSNR结果可知，与中值滤波、高斯滤波和维纳滤波算法相比，BM3D算法处理效果的稳定性较差. 而BM2D+1D算法弥补了BM3D算法稳定性差的不足，在处理噪声图像时能保持运行的稳定性，从而得到优于中值滤波、高斯滤波和维纳滤波算法的去噪效果.

记录仿真过程中算法的运行时间，对于含高斯噪声的图像，BM3D算法的运算时间为23.810 4 s，BM2D+1D算法的运算时间为14.384 9 s，运行时间降低了39.6 %. 优化的BM2D+1D算法不仅RPSNR值有所提高(比BM3D提高了0.388 dB)，而且在运算时间上也有一定程度的减小.

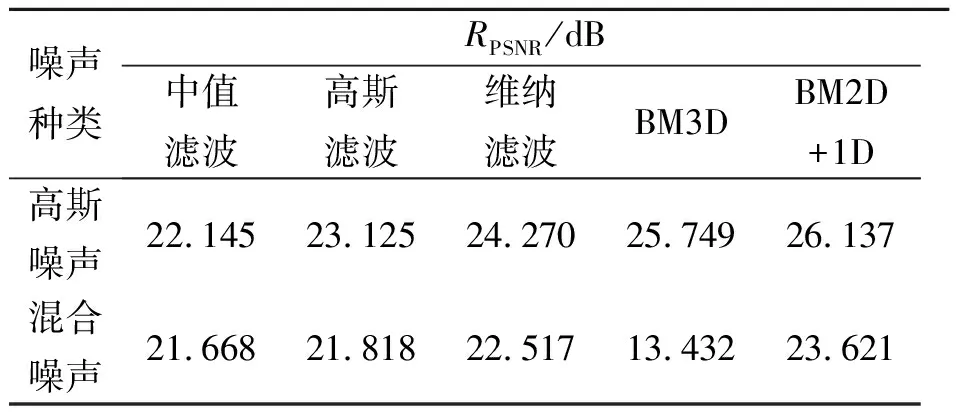
表1 5种去噪算法的RPSNR值

3 Canny边缘检测算法

图像的边缘是指灰度、纹理或颜色等特征突变的位置，在图像分割过程中对区域识别将起到重要作用. 但是在实际情况下，受噪声干扰得到的图像边缘常常模糊，导致边缘提取变得更加困难. Canny算法对受高斯白噪声干扰的图像边缘检测效果较好[13]，该算法主要有以下4个步骤：

1)利用高斯滤波器平滑图像. 通过对滤波像素点及其相邻像素点进行加权均值计算，去掉图像中的噪声点.

针对该块应力特点，采用直井长缝结合定向射孔工艺，有效降低裂缝起裂的复杂程度，并配合暂堵剂＋组合陶粒降低滤失，提高压裂液的使用效率。

2)计算梯度幅值和方向.计算图像在x和y方向上的梯度值Gx和Gy，由此得到梯度幅值和方向角[14]为

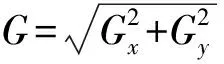
(9)

(10)

3)对梯度幅值进行非极大值抑制.根据梯度方向对图像上每个点的梯度幅值进行非极大值抑制[15]，实现边缘估计.

4)利用双阈值检测并连接边缘.通过双阈值设置来检测边缘，用高阈值M1将背景与提取的轮廓进行分割，用低阈值M2对边缘进行平滑.将像素值在M1～M2间的点作为弱边界，将像素值大于M1的点作为强边界.当M1设置过大时，会导致边缘轮廓断续，此时可以通过弱边界八连通邻域内是否存在强边界进行判断，存在弱边界与强边界相连接的情况下，该弱边界才能被视为边缘点进行连接[16].

4 Canny算法优化及仿真实验

由于去噪处理后的轨道图像中仍然会存在干扰信息，使得Canny算法在检测过程中出现偏差. 因此，利用图像增强算子对Canny算法进行改进，使得缺陷检测结果更加完整和准确.

4.1 Canny算法的优化

根据Canny边缘检测算法原理可知，Canny算法是通过高斯去噪来降低噪声干扰. 高斯去噪会使图像的边缘信息被削减，需要选择合适的高斯半径才能保留较为完整的边缘信息[17]. 而轨道图像预处理环节已经对图像进行了去噪处理，并且得到了较好的去噪结果. 故可以将高斯滤波从Canny算法中去除，以降低算法的运行时间.

另外，由于图像预处理环节在一定程度上模糊了边缘信息，生成无意义像素信息，导致后续阈值选取范围受限，不利于边缘信息的提取. 因此，在Canny算法中加入LOG算子和Gamma算子对预处理结果进行边缘强化，滤掉一部分虚假边缘信息，进一步减少算法的运算时间，降低算法运算复杂度.

l=cLOG(1+vr)，

(11)

其中，c为常数(通常设为1)，系数v=1,r∈[0,1]为输入的归一化灰度值.

2)利用Gamma变换算子对图像进行校正，将图像的高、低灰度进行修正改进，增强图像的对比度[18]，输出图像表示为

s=Auγ，

(12)

其中，A为常数(通常设为1)，系数γ=3，u∈[0,1]为输入的归一化灰度值.

优化的Canny算法不再考虑噪声干扰，并利用LOG算子和Gamma算子对去噪结果图像进行对比度调整及边缘强化，增强轨道缺陷处信息，均衡各部分像素灰度，从而过滤虚假边缘和无意义边缘的像素点. 与增强前的图像相比，优化后的边缘信息更加清晰，算法阈值调节更加灵活. 可根据实际采集的图像自适应调节阈值大小，得到保留完整轨道缺陷边缘信息的结果图像.

4.2 仿真实验

在与上述实验相同配置的计算机上进行测试，以BM2D+1D算法对高斯噪声图像去噪结果[图4(f)]为例，将优化后的Canny算法应用到去噪图像的边缘检测中，得到不同阈值M下的结果，如图6所示.

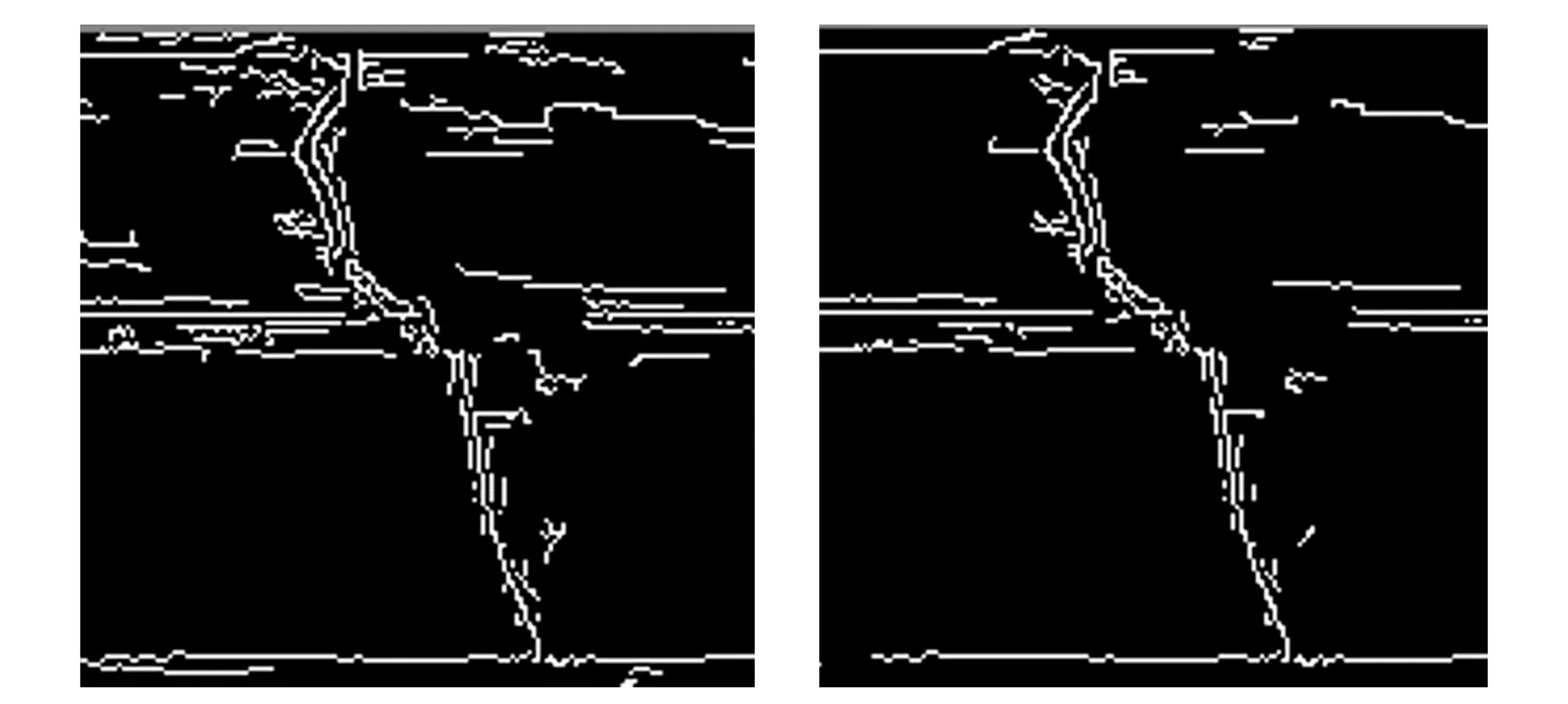
(a)M=50 (b)M=75

(c)M=100 (d)M=125

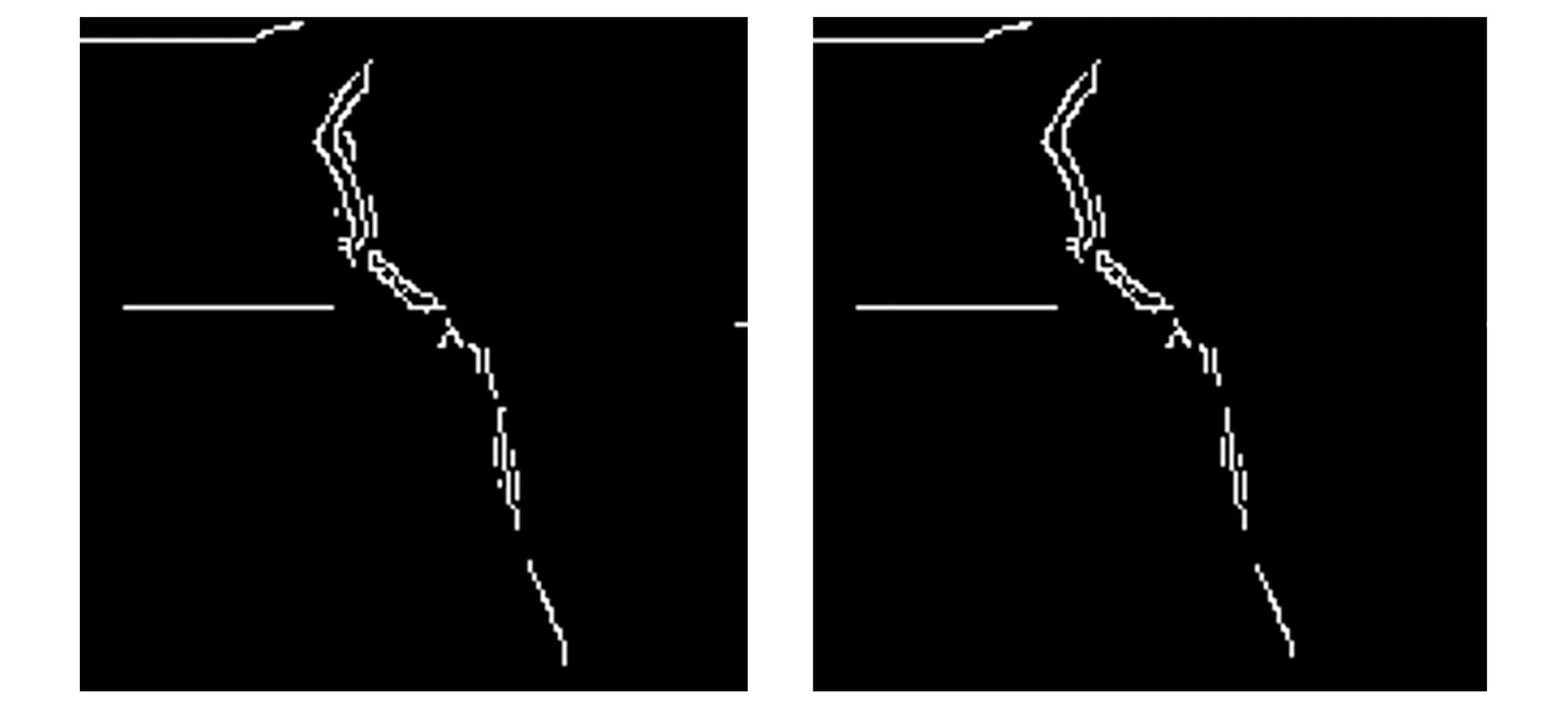
(e)M=150 (f)M=175

(g)M=200 (h)M=225图6 优化的Canny算法二值图像结果

从图6中可以看出，当M=100时，优化的Canny算法可以完整保留重要边缘信息，从横纵方向可以看出轨道的擦伤和裂痕. 当M>150时，轨道裂痕边缘开始出现断续，从而无法捕获完整的边缘信息. 因此，为得到准确的边缘信息，在算法阈值调节上需要进行严格控制，使得算法尽可能完整地保留轨道裂痕边缘信息，并尽可能多地去除无意义像素点.

经典Canny算法中包含高斯去噪过程，并且由于边缘信息被模糊而产生虚假边缘信息，增加了算法工作量. 优化后的Canny算法减少了高斯去噪步骤，并加入LOG算子和Gamma算子解决了虚假边缘信息过多的问题，优化了算法运算流程和运算量. 优化前的平均运行时间为0.017 2 s，优化后的平均运行时间为0.003 2 s，运行时间降低了81.4%.

5 结 论

对轨道缺陷图像检测算法进行了优化. 通过改进BM3D算法的三维变换方式，将其转化为BM2D+1D算法，作为轨道图像预处理方法. 在图像质量评价指标和运行效率上，BM2D+1D算法具有一定的优势. 对于含高斯噪声的图像，BM2D+1D算法的RPSNR值提高了0.388 dB，运行时间降低了39.6%. 同时，优化的Canny算法可以滤除图像中大部分多余的边缘信息和无意义的像素信息，实现对轨道缺陷的边缘增强和边缘检测，得到了完整的轨道缺陷边缘信息，优化后的算法运行时间降低了81.4%.