利用悬臂梁测量材料的弹性模量
翦知渐,周艳明,谢 中,周正贵
(湖南大学 物理与微电子科学学院 大学物理实验中心,湖南 长沙 410082)
弹性模量是弹性材料的重要力学参量,在工程设计和应用中弹性模量是非常重要的参量,测量弹性模量也是理工科大学物理实验中常见的实验项目. 弹性模量的测量方法有很多种,如动态的共振法[1-2]、声速测量法[3],静态的拉伸法[4-7]以及梁弯曲法[8-10],等等. 在拉伸法和梁弯曲法中,因为形变较小,大多采用技术与方法相结合的方式对形变进行测量,如光学方法测量[4-6,8-9]、应变片[7]、霍尔传感器[10]等,这些方法各有特点,适用于不同场合和要求.
在梁弯曲法中,主要有激光光杠杆测量法[9]、霍尔位置传感器法[10]、单缝衍射法[11]、光纤布拉格光栅测量法[8]等. 它们共同的特点是:将横梁的两端用刀口支撑,在横梁中间位置用刀口施加作用力使其产生弯曲,通过测量梁的挠度来求得弹性模量. 在采用各类传感器测量挠度时,传感器需要定标,测量结果还会受到传感器的温度效应等干扰,因这种方法产生的形变较小,从而使得测量结果的重复性较差,误差也较大.
为解决上述问题,在悬臂梁自由端上方贴全反射镜,用固定方向的激光束照射反射镜,反射光斑投射至标尺面. 在悬臂梁上施加载荷使其产生弯曲,反射镜将会随载荷的增加而产生转动和下移,反射光斑的位置将会移动较大距离,这个距离可通过标尺测出. 光斑移动距离与悬臂梁自由端转角和挠度有确定的关系式,根据该关系式即可求出材料的弹性模量.
1 测量原理
如图1(a)所示的矩形截面梁,厚度为d,宽度为l.如果d,l相对于梁的长度小很多,则该矩形梁可看作是1根细长杆.当细长杆的弯曲变形较小时,可利用小挠度理论[12]来计算梁的挠度和转角.
(a)矩形截面梁
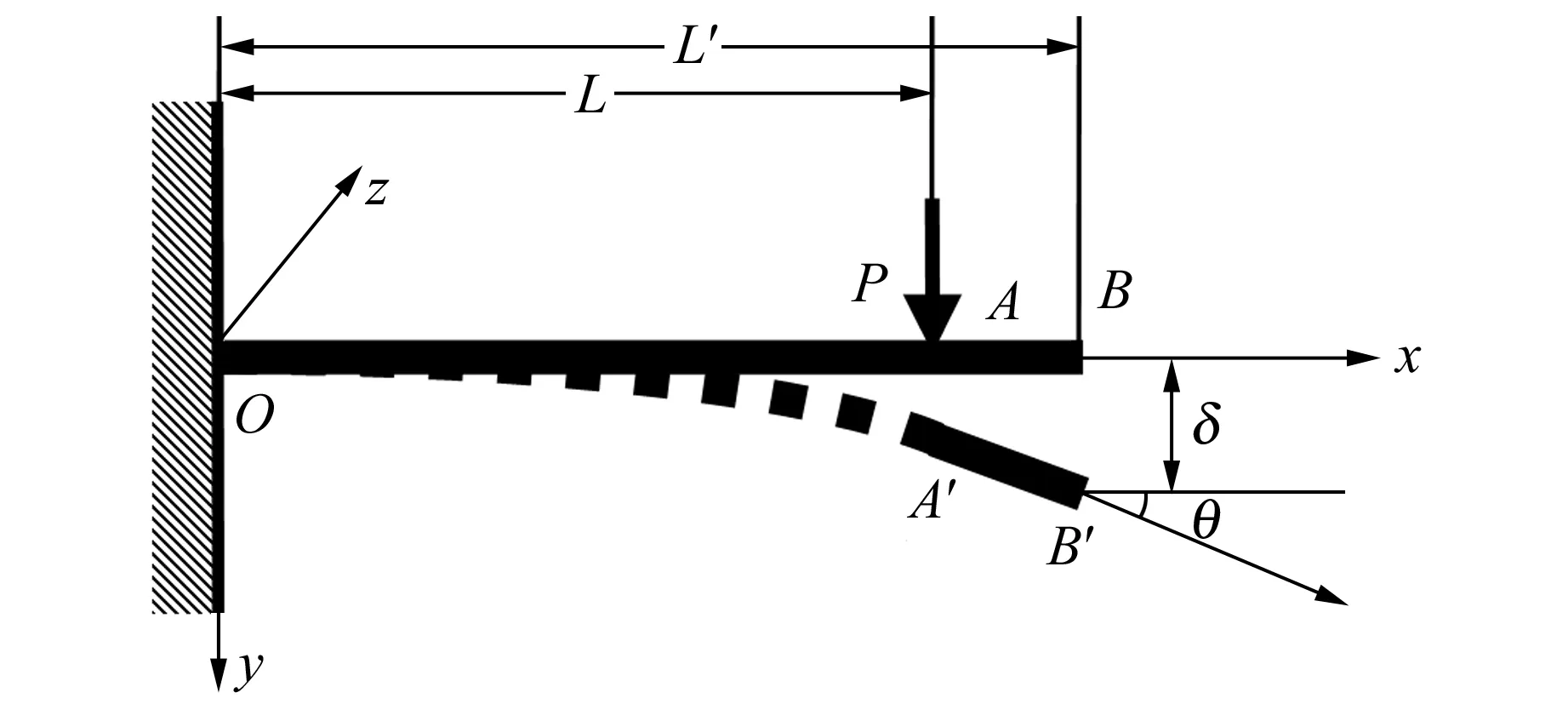
(b) 悬臂梁端点施加载荷P后的弯曲图1 实验装置示意图
将悬臂梁固定在O点,在A点(与固定端距离为L)施加集中载荷P,悬臂梁将产生弯曲(AB段没有变形),如图1(b)所示.自由端转角为
(1)
其中,E为材料的弹性模量,I为悬臂梁绕z轴的惯性矩,其表达式为
(2)
离O点距离为L′处,梁的挠度为
(3)
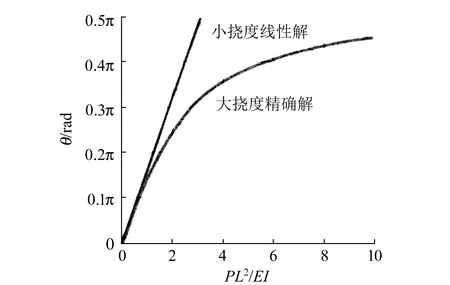
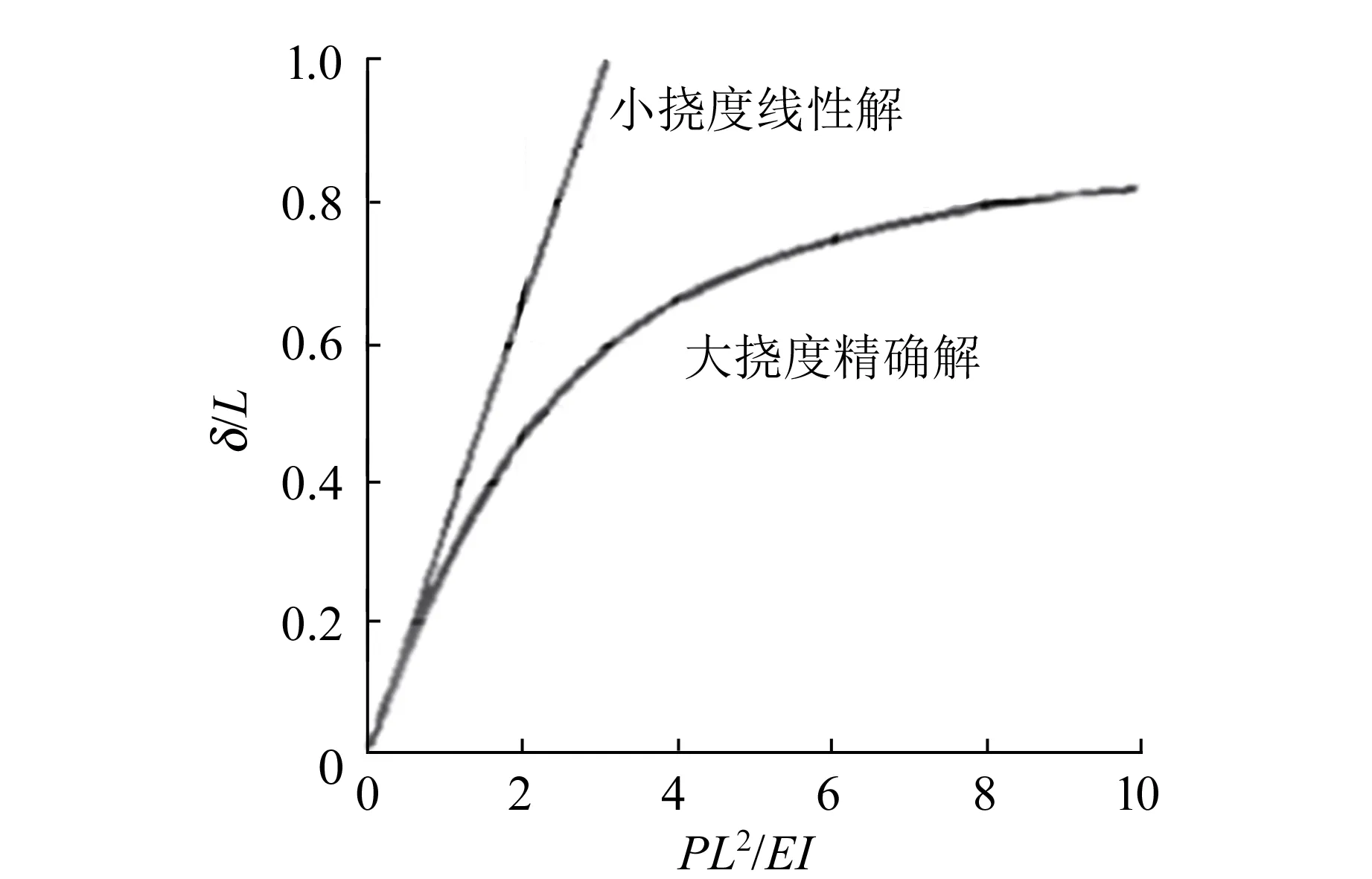
根据式(1)~(3),在小变形条件下梁自由端的转角和挠度与载荷的关系是线性的,如图2所示[12].
(a)自由端转角的计算结果
(b)自由端挠度的计算结果图2 小挠度线性解与大挠度精确解的比较
如果形变较大(大挠度),则转角和挠度的表达式不再是线性的,可由弹性理论给出精确解(见图2).故小挠度理论(线性关系)成立的条件是:
1)自由端转角θ<π/10;
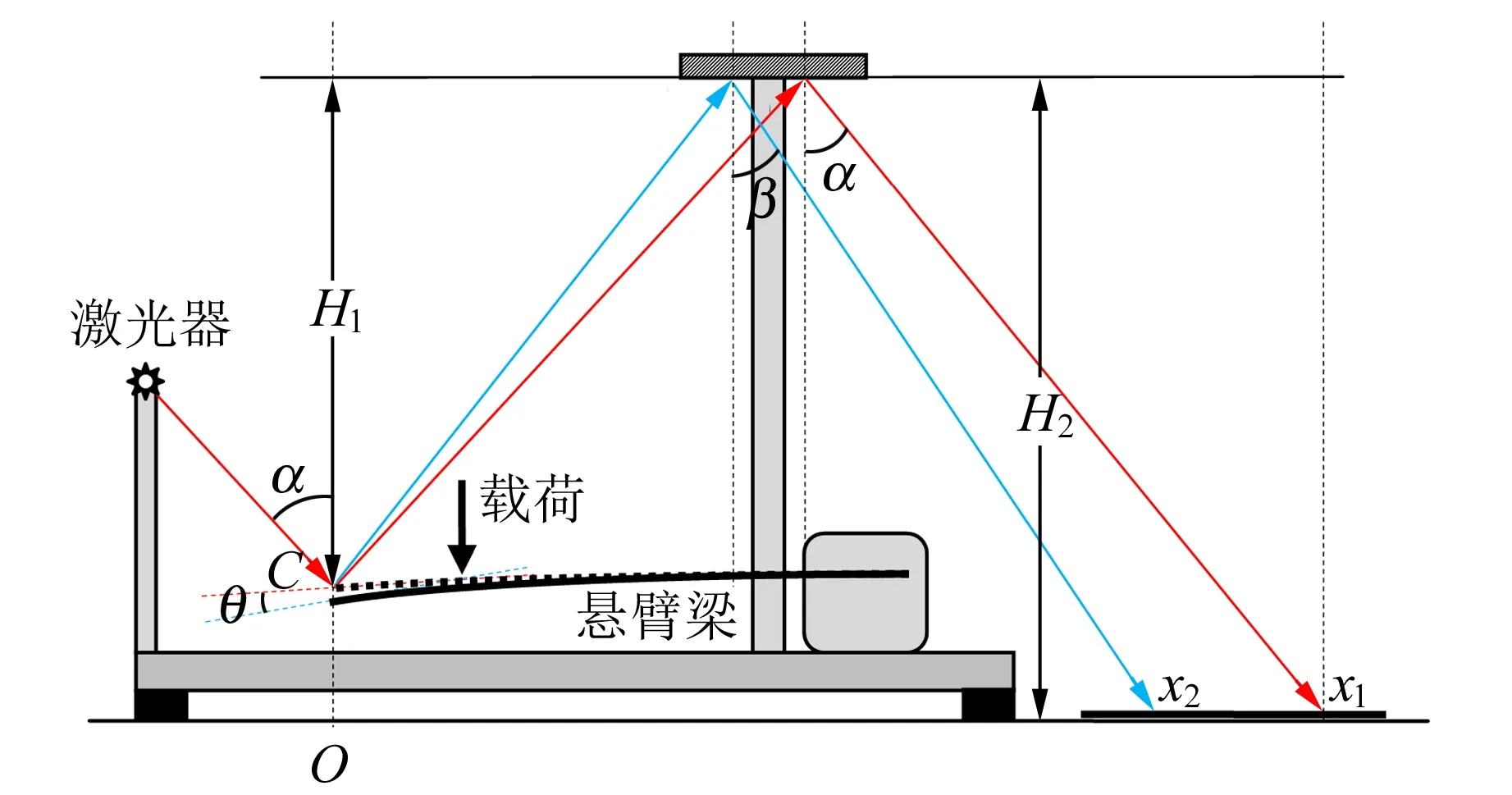
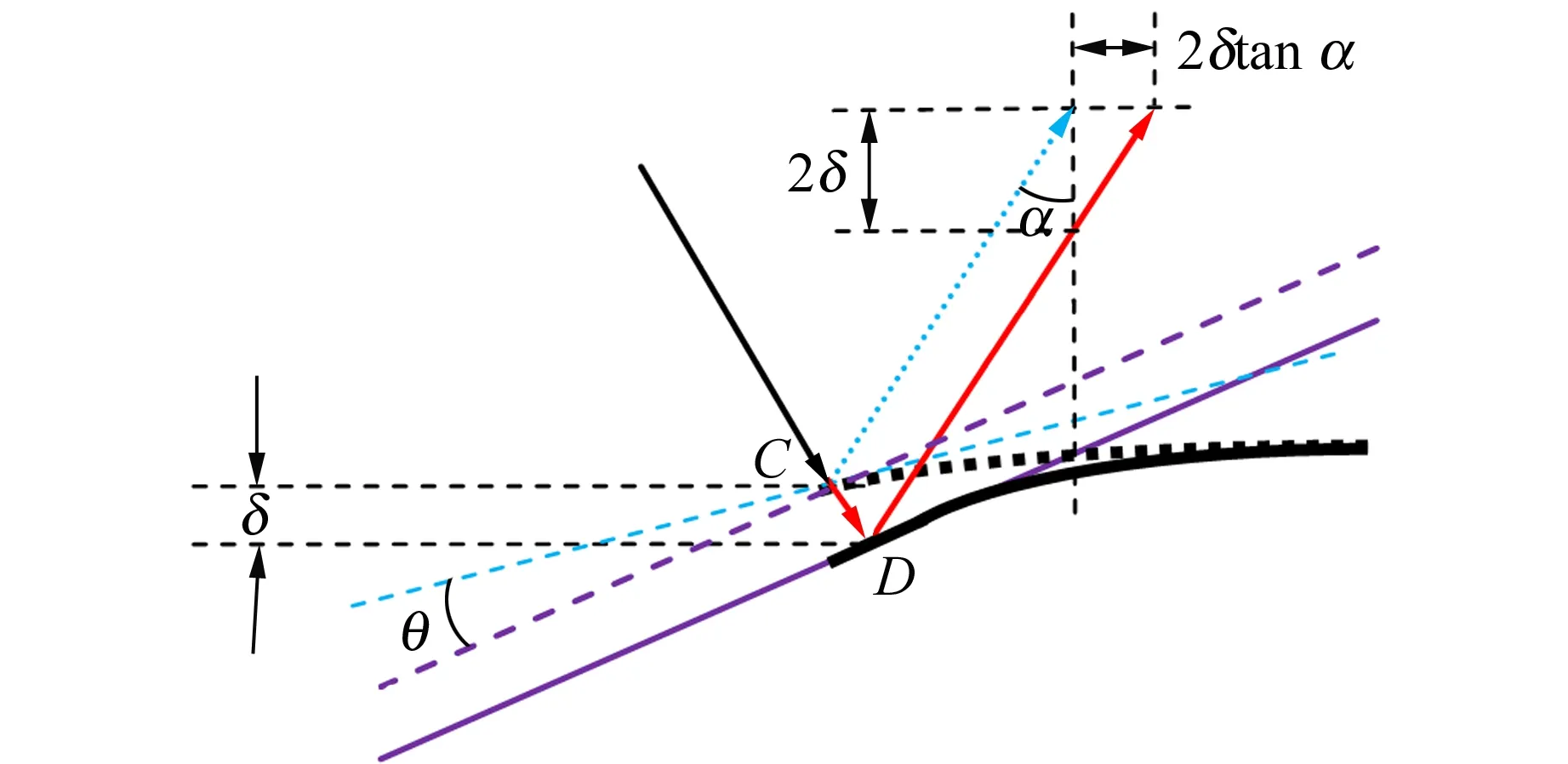
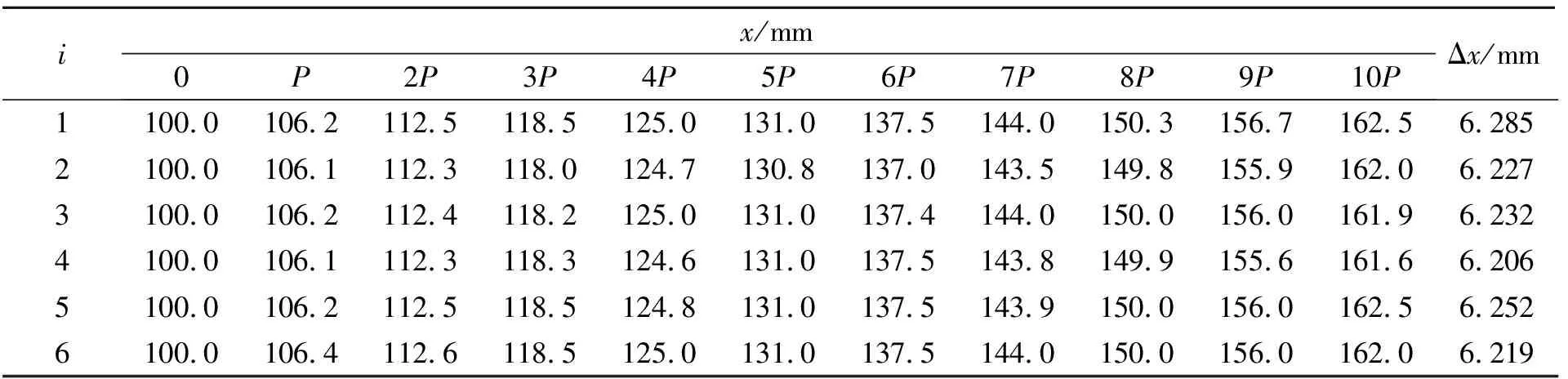
2)自由端挠度δ 当以上2个条件均得以满足时,就有θ∝P和δ∝P.这就意味着,在小挠度情形下梁的变形可以根据载荷直接叠加计算(包括自重引起的形变). 如果测出一定载荷P下悬臂梁的自由端转角θ,则根据式(1)即可计算出材料的弹性模量E. 如果施加的载荷不是作用在某一点的集中载荷,而是在某一区域施加均匀载荷Q,如图3所示,相应的计算公式为 (4) 图3 悬臂梁施加均匀载荷后的弯曲 对θ的测量可利用光杠杆对小角度进行放大来进行.实验装置如图4所示,在梁的自由端上方贴1面全反射镜,激光被反射至标尺面形成细小光斑.随着载荷的增加,镜面发生转动,光斑将会沿标尺面向左移动,测出光斑移动的距离即可得出θ的变化.为了获得较大的放大倍数,同时使得仪器占用空间小、观察方便,本文采用了折叠光路.下面分别讨论转角和挠度变化对光斑移动的影响. 如图4所示,考虑自重及贴上反射镜的关系,悬臂梁未加其他载荷前,自由端镜面初始位置沿红色虚线(悬臂梁挠曲线自由端的切线)方向,此时反射光与竖直方向的夹角为α,经上方反射镜反射后光斑位于x1处.若原点设为O,可知x1=(H1+H2)tanα. 图4 光斑位置与梁自由端转角的关系(α ≈ 45°) 加上小载荷P后,悬臂梁弯曲,镜面转动θ角到了蓝色虚线方向,反射光斑移到了x2处.镜面转动θ角,则反射光方向转动2θ角,即β=α-2θ.因此,光斑移动距离为 Δx=x2-x1=(H1+H2)(tanβ-tanα)= -2(H1+H2)(1+tan2α)θ+O(θ2). (5) 当载荷增加时,光斑将向左移动,即x的读数减小. 仔细检查光路会发现,施加载荷后,梁的挠度增加了δ,即镜面向下移动了δ,所以光的反射点实际上是D而不是C,如图5所示,这导致光斑向右移动了一段距离,即x的读数增加. 图5 光斑位置与梁自由端挠度的关系 考虑到悬臂梁基本是水平的(θ很小),所以光斑移动距离的修正项为2δtanα(近似带来的偏差属于θ的高阶项),如图5所示.经过修正后,式(5)可改写为 Δx=-2(H1+H2)(1+tan2α)θ+2δtanα= (6) 式(6)为光斑移动距离Δx与悬臂梁自由端转角θ之间的关系式.因实验中所加载荷P很小,所以悬臂梁的形变也很小(一般最大转角θmax≤5°),且θ的高阶项影响也非常小,故式(6)是线性度较好的表达式.实际测量结果也证明了这一点. 调试好实验装置后,在距端点L处加上载荷P,测出其对应的Δx.根据式(1)和式(6)可得 (7) 其中,惯性矩I的值由式(2)得出. 采用等量增重的方法进行多次测量以改善结果,同时该测量方法可以检验载荷与形变的线性关系,并用线性拟合来处理数据.假设进行n次测量,每次加的载荷分别为P,2P,…,nP,相应的反射光斑位于x1,x2,…,xn,线性拟合式为 xn=A-kn, (8) 其中,A为常量(与原点选择有关),斜率k即为施加载荷P时的Δx.将Δx代入式(7),即可得到待测试件的弹性模量. 利用图6所示的仪器对几种常见材料进行测试. 首先用等量增重的方法测试了形变与载荷的线性关系,结果如表1所示. 表中P为单个砝码的重力. 已知单个自制砝码的质量为9.28 g,本地重力加速度为9.79 m/s2,故P=0.090 85 N;Δx为各组数据按照式(8)进行线性拟合的斜率. 对表1中的数据做线性拟合,其拟合度R2均在0.999 8以上,充分说明二者有良好的线性关系. 由于实验使用的自制砝码,每个砝码约有0.02 g的偏差,这可能是影响线性拟合度的因素. 图6 测量仪器实物图 不同测试者在不同时间下对宽度为l=25.00 mm的铝合金试件进行多次测量,结果见表2. 根据表中数据,得到铝合金的弹性模量E=(7.056±0.052)×1010N/m2. 作为对比,在本校材料实验室用电测法对所测试件进行了测量. 将该方法所用的试件制作成如图7所示的形状,测得其弹性模量分别为7.49×1010N/m2和7.05×1010N/m2,二者均在误差范围内. 但电测的结果离散性很大,而使用本文方法进行测量,结果的重复性较好(见表2):7次测量结果的标准差为0.08,相对偏差约为0.1%. 表1 光斑移动距离与载荷的关系(铝合金) 表2 铝合金的弹性模量实测结果 图7 电测试件 对不锈钢试件的测量过程与对铝合金的测量过程相似. 多次测量的结果为E=(2.072±0.010)×1011N/m2. 一般钢材的弹性模量在1.95×1011~2.10×1011N/m2之间,因合金的弹性模量与其成分、工艺甚至生产批次均有关系,试件在加工时的应力残留(硬化)也会影响其弹性模量. 实验采用的试样是经剪板机裁剪加工而成的,残余应力较大,测量结果应大于没有残余应力的材料. 通过以上的实测结果,可以看到使用本方法测量材料的弹性模量,其结果的重复性较好,不确定度也较小,充分说明了本实验方法及测量装置的稳定性较好,测量结果的精确度较高. 设计的弹性模量测量装置不需要使用刀口支撑横梁,也不需要使用刀口施加载荷. 采用悬臂梁结构,小载荷也能使得样品产生较大的形变,经估算,悬臂梁自由端的挠度要比两端支撑梁的中部挠度大1个数量级以上. 光斑移动距离因自由端挠度和转角的改变将会变得较大,因此测量精度较高. 通过选择试件的厚度能将测量数据控制在预定的标尺读数区内,从而能够在同一装置上方便地测量弹性模量相差很大的固体材料. 只要预估待测材料弹性模量的数量级,大致确定试件的厚度,例如高强度材料样品厚度稍薄,低强度材料样稍厚,就能控制形变大小(与样品厚度的三次方成反比). 因光斑移动距离与形变成正比,所以很容易做到在合适的标尺区内进行读数. 该方法不使用传感器加力,也不采用各类测位移的传感器,避免了传感器定标、温度漂移等问题. 实验结果的重复性好,具有良好的实用性. 该实验装置小巧,结构简单,操作方便,特别是样品易于加工,适用于测量弹性模量跨度值很大的各种材料.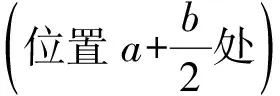

2 测量装置
2.1 自由端转角变化对光斑移动的影响
2.2 挠度变化对光斑移动的影响
2.3 测量方法
3 实测结果及分析



4 结束语

