双光子纠缠实验教学系统的搭建与应用
王 伟,刘国超,傅兆瑢,王晨冰,李 智,张朝晖
(北京大学 物理学院,北京 100871)
量子信息科学在过去几十年得到了快速发展,量子保密通讯和量子计算等新兴技术不仅吸引了众多领域科学家的关注,也引起了大众的广泛兴趣. 目前在本科物理实验教学中开展量子信息相关实验的大学很少,学生对其的了解基本是抽象的理论学习,理解难度较大. 北京大学基础物理实验教学中心开发的双光子纠缠实验教学系统将抽象的量子相关概念通过实验清晰地展现,使学生通过做实验加深对量子纠缠的理解和相关理论及应用的深层次思考.
量子纠缠态在量子物理研究领域中占据重要地位,同时又是量子信息技术中的基础和核心. 与传统信息处理方式不同的是,在量子信息论中利用的是量子纠缠态本身,其基本任务是量子纠缠态的制备、存储、操纵、传输与读出. 光子纠缠态是最常见的量子纠缠态之一,被应用到许多高新技术领域,如量子隐形传态、量子传真、量子保密通讯、量子计算等. 非线性晶体中的自发参量下转换(Spontaneous parametric down conversion,SPDC)过程是目前最普遍的光子纠缠态制备方案,本实验教学系统即是对偏硼酸钡(BBO)晶体的SPDC效应产生的双光子纠缠态的制备、测量和分析.
1 系统原理
1.1 量子纠缠和Bell不等式
量子纠缠是指1个量子系统的状态和另1个量子系统密切相关. 例如简单的自旋纠缠态表示为
(1)
假设1对粒子处于自旋纠缠态, 那么粒子的自旋方向无法确定,但是如果测到1个自旋粒子向上,就可得知另1个粒子自旋向下;反之亦然.纠缠的2个自旋粒子处于这种奇妙的相互依赖关系.除了自旋之外,还可以构造位置、动量、能量、光偏振的纠缠态.
在量子力学诞生初期,纠缠这样的纯量子效应面临很多争议. Einstein,Podolsky和Rosen(EPR)的“局域实在”或隐变量理论是最著名的反对观点[1]. Einstein等人认为“通过测量1个系统,就能立刻知道另1个系统的状态”是荒谬的,是不可能存在的超距作用. 他们认为应该用隐变量来解释量子力学的波函数,量子力学理论仍应该是决定论,其不确定性是因为存在一些我们所不知道的隐变量. 以Bohr为代表的哥本哈根学派则认为应该用概率来描述世界,量子力学不能算是系统的状态,但是可以确定每个状态出现的概率. 为了定量地刻画这一观点,1964年,J.S.Bell基于局域隐变量理论提出了实验上可测的Bell不等式[2]. 后来Clauser,Horne,Shimony和Holt将其推广为CHSH不等式[3]. 设有2个物理系统A和B ,每个系统各有2个可测物理量,分别为a,a′和b,b′,其测量值只能取±1.2个系统同时测量其中1个物理量,例如a和b,记测量结果乘积的平均值为E(a,b),则
S=-E(a,b)+E(a,b′)+E(a′,b)+E(a′,b′).
(2)
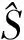
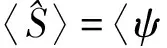
(3)
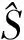
1982年,Aspect等人[4-5]用钙原子的雪崩反应发生纠缠光子的实验,首次测量到违背CHSH不等式的现象. 之后的几十年中,不断有实验物理学家在不同的实验系统中观测到该现象[6-10].
参考1995年Kwiat等人的工作[11],本文搭建了稳定、可靠的实验装置,利用自发参量下转换效应制备出双光子偏振纠缠态并进行测量,证伪了Bell不等式(或者CHSH不等式),从而排除局域隐变量理论.
1.2 纠缠态的制备
自发参量下转换(SPDC)是二阶非线性光学效应[12-13]. 当1束强泵浦激光照射在非线性晶体上,1个泵浦光子有一定概率产生1对频率更低的光子,分别称为信号光和闲频光,该过程需要满足能量守恒和动量守恒(相位匹配)
ωp=ωs+ωi,kp=ks+ki,
(4)
其中,p,s和i分别表示泵浦光、信号光和闲频光,ωp,ωs和ωi分别表示泵浦激光、信号光和闲频光的角频率,kp,ks和ki分别为泵浦激光、信号光和闲频光的波矢.据此可以推算出出射光角度和晶体参量、入射光波长的关系.
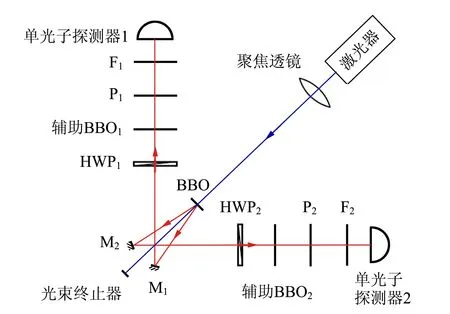
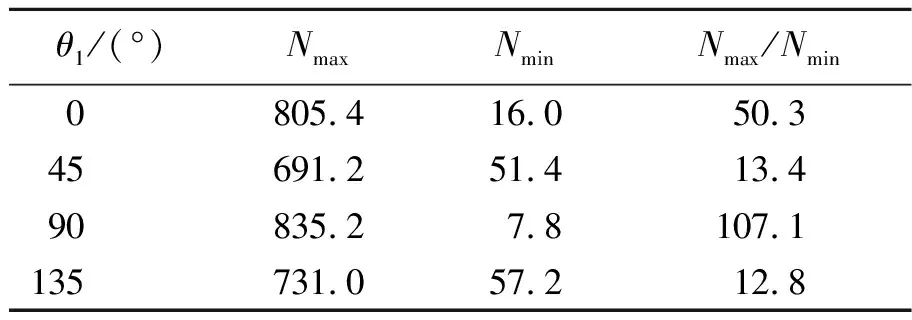
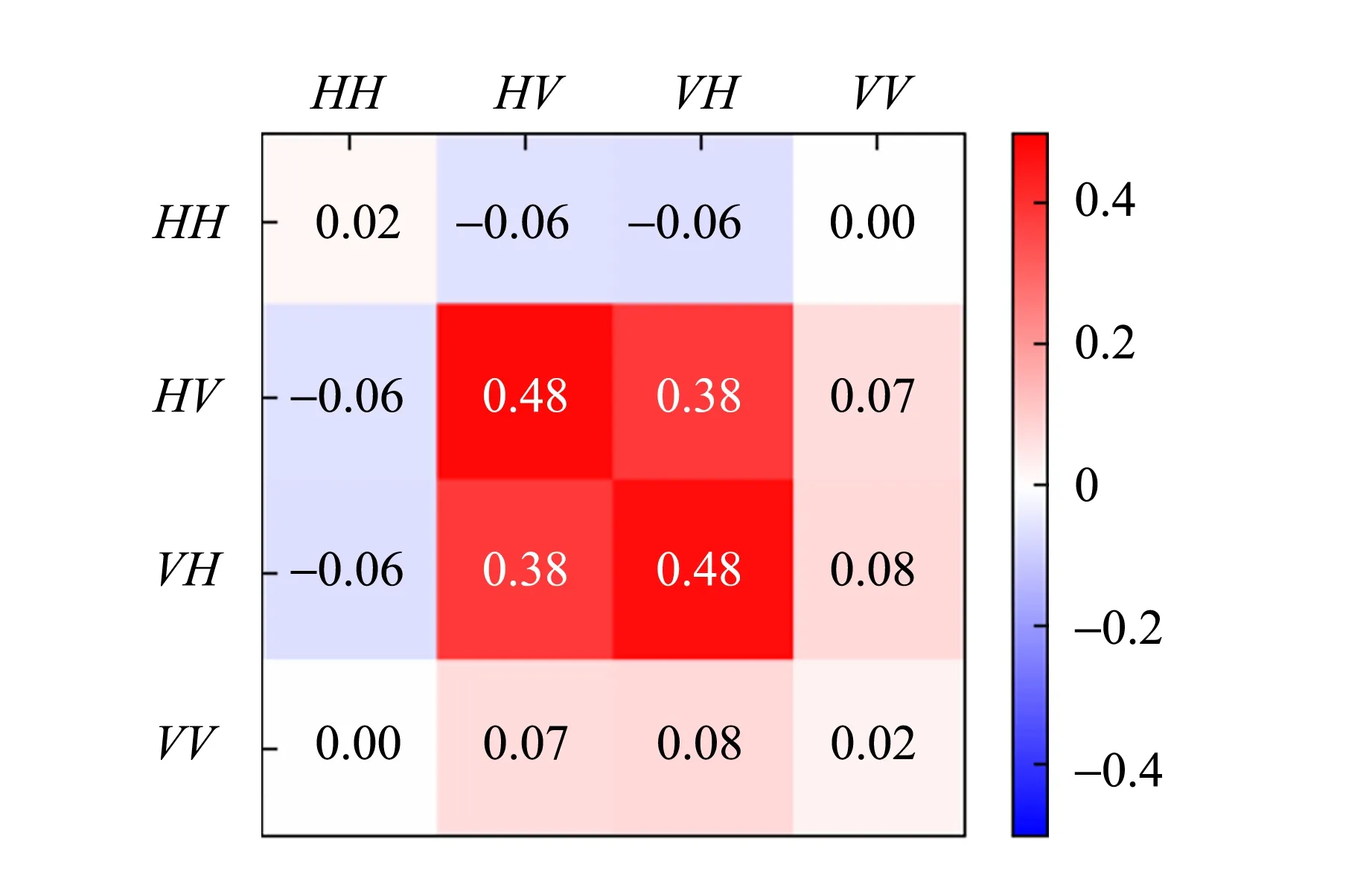
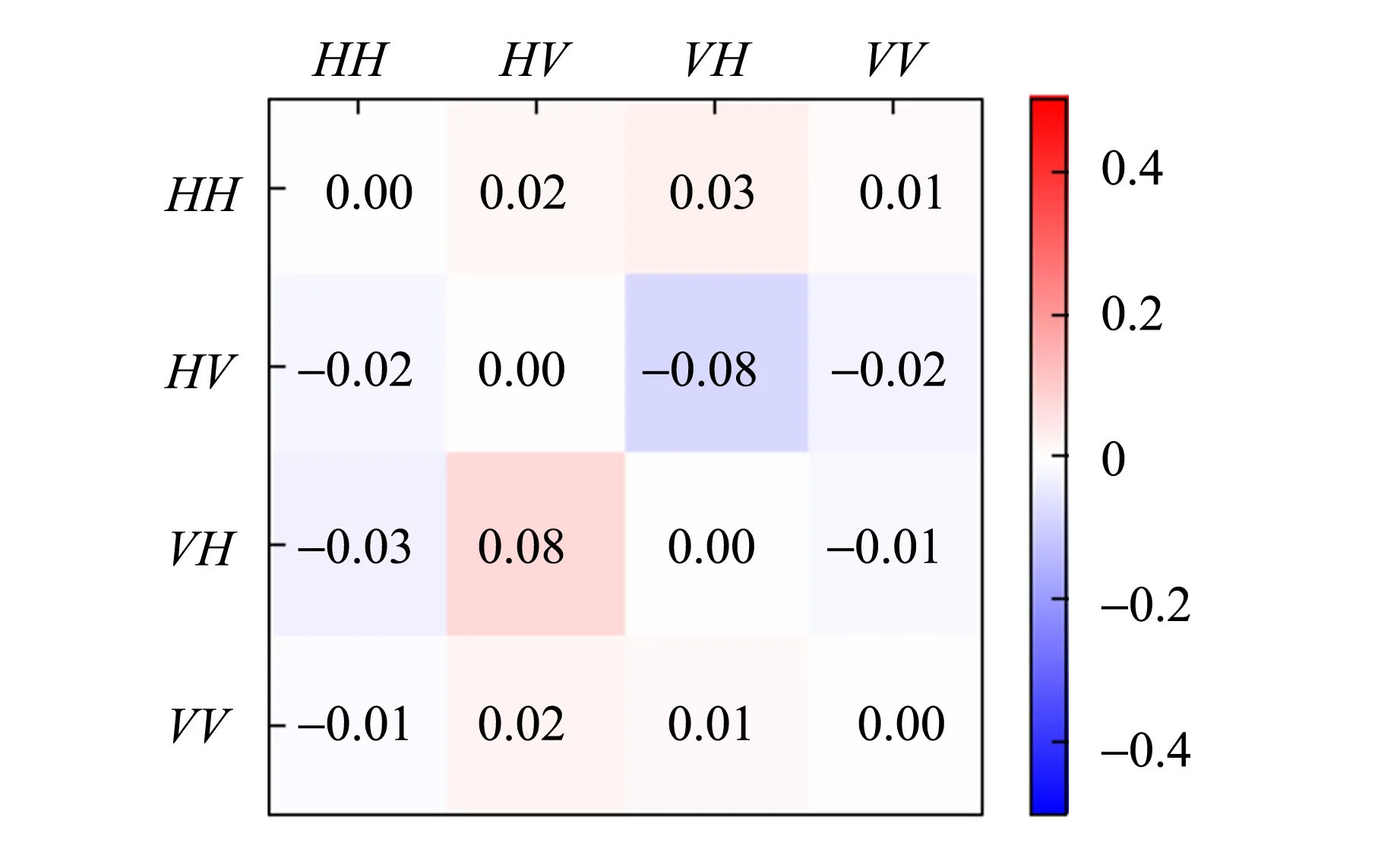
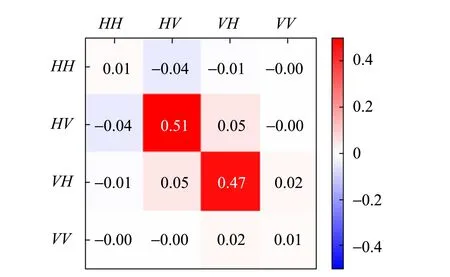
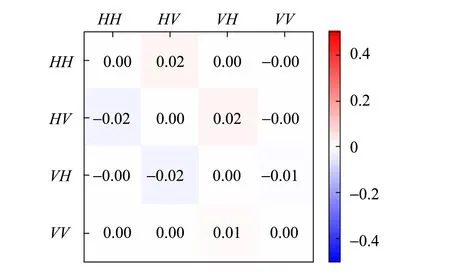
根据信号光和闲频光的偏振特性不同,可以将SPDC分为2种类型. 对于实验使用的BBO晶体(负晶体ne 根据相位匹配条件[式(4)],II类转换发射的ωs=ωi的光子分别形成2个光锥,其中1个光锥为o光,另1个光锥为e光[14],且晶体的切割面不同使得泵浦激光入射时与晶体光轴夹角不同,出射光方向也发生变化,表现为2个光锥相离、相切或相交. 当2个光锥相交时,如图1所示,2个交点处的光子对可以用以下偏振纠缠态描述[15] (5) 其中H,V分别代表水平和竖直偏振光子. 图1 II类SPDC示意图 实验采用的BBO晶体的晶体光轴与Z轴夹角θ=42.6°,根据式(4)计算可得交点处的光子出射方向与泵浦激光方向的夹角为3.6°. 纠缠态的测量就是对光锥交点处的纠缠光子进行采集和分析. 当使用偏振片测量光子偏振时,光子将坍缩到2个偏振本征态之一:偏振方向平行于偏振片透振方向(表现为通过),偏振方向垂直于透振方向(表现为不通过). 规定光子通过偏振片记为1,不通过记为-1. (6) 任意选取4组(θ1,θ2),进行偏振符合测量,可以得到CHSH不等式所要求的4个偏振关联函数.对于偏振纠缠态[式(5)],量子力学给出 N(θ1,θ2)∝sin2(θ1+θ2) , (7) E(θ1,θ2)=cos [2(θ1+θ2)] , (8) 式(7)~(8)结果可以体现出量子纠缠效应.对于1个纠缠态,测量其中1个光子的偏振,如果测量结果为H,则另1个光子的偏振态会立刻坍塌为V;如果测量结果为V,则另1个光子的偏振态会立刻坍塌为H.该现象表面看似为超距作用,本质是量子纠缠. 在双折射晶体中,一般情况下,除沿光轴方向传播的光或偏振方向平行于主介电轴的光,光的波矢方向与能量传播方向并不相同. 对于单轴晶体,o光在晶体中的波前传播方向与能量传播方向一致,而e光波前传播方向与能量传播方向不一致,这导致波矢方向相同的o光和e光在传播过程中逐渐分开,称为走离(walk-off)效应. 在二次谐波产生等非线性过程中,由于光束截面有限,走离效应限制了不同偏振光束之间的交叠区域,会降低非线性过程的效率. 因此在量子纠缠实验中,双折射效应会导致下转换光子在晶体内产生横向空间走离与纵向时间走离[11],导致纠缠度降低,必须加以补偿. 具体补偿措施是在下转换后的光路中加入45°放置的808 nm半波片和厚度为主BBO晶体厚度1/2的辅助BBO[11,15]. 补偿原理是若下转换光子在主BBO晶体中产生光程差,其走离大小相当于由晶体的一半厚度产生. 出射的o光和e光经过45°放置的半波片,其偏振方向各自改变90°,即原来垂直偏振的e光变成水平偏振的o光,而原来水平偏振的e光变成垂直偏振的o光,再进入辅助BBO. 由于主BBO与辅助BBO晶体空间取向完全相同,所以两光子改变偏振方向再经过辅助BBO晶体后,其在主BBO晶体内由于双折射效应产生的横向空间走离和纵向时间走离都得到完全补偿. 若下转换不是发生在主BBO的正中间,但只要下转换发生在泵浦光的横向相干长度内,在主BBO中间两侧相等距离上光子发生的走离是不可区分的,相干性仍然可以恢复. 图2为实验光路示意图. 405 nm紫色泵浦激光从激光器出射后,经过凸透镜聚焦在主BBO晶体上. 主BBO晶体发生SPDC效应产生光子,其中810 nm纠缠光子对相对泵浦激光在水平面内有一确定的角度偏离(图1),在位于此偏离角度的2个路径上分别放置反射镜M1和M2,则可以将2个纠缠点捕捉到光路中并分别经反射镜M1和M2反射后,依次通过一系列元件到达光纤耦合器. 再由准直透镜耦合进光纤,然后通过单光子探测器1和2将探测到的2路信号输入符合系统,最终得出2路的光子计数和符合计数. 从反射镜到光纤耦合器的光路上,依次有:45°放置的808 nm半波片HWP、辅BBO晶体(用于补偿走离)、偏振片P[用于确定测量方向(θ1,θ2)]、810 nm窄带滤光片F(用于消除杂散光). 为了实验安全以及尽量降低杂散光影响,还在光路中设置了光束终止器收集剩余激光. 在搭建系统时,为使装置更稳定、更紧凑,激光器被安置在光学平台下方,405 nm激光经过焦距为50 cm凸透镜聚焦,再经过2个激光反射镜反射,最后从光学平台钉孔出射打到BBO晶体上. 装置实物如图3所示. 图2 实验光路示意图 由于SPDC效率很低,且810 nm出射光子对不在可见光波段,难以直接确定其具体路径,为光路调节带来了很大困难. 为了实现对光路快速有效地调节,设计了反打光调节方法,即将光纤耦合器上光纤的输出端接650 nm红激光,变为红光的输入端,红光沿着光路逆向传播. 根据光路可逆,红光反向模拟了810 nm纠缠光子对的行进路径,让不可见的SPDC光变得“可见”,从而辅助实现光路的初步搭建. 具体操作时通过调节光纤耦合器的位置和反射镜M1和M2改变红光的出射方位,使得在主BBO晶体处2路红光和紫色泵浦激光三光重合,且2路红光分别打到预先设置好的标记点上(标记点的位置由光子对出射角和标记卡到主BBO晶体距离计算得到,光子对出射角由相位匹配条件计算得出),如图4所示. (a)实物图 (b)电路板图3 装置实物图 图4 反打光标记点实物图(405 nm激光从标记卡中心小孔出射) 重新将光纤接入单光子探测器,此时从晶体以一定角度出射的纠缠光子,能够被光纤耦合器探测接收到,实现了光路的基本搭建. 如果要让光纤耦合器接收到纠缠的全部信号光和闲置光,仍需要进一步细调. 作为本科生的教学实验,要达到良好的教学效果,实验步骤的设计至关重要. 经过长时间摸索,制定了适合学生操作的、重复性良好的实验步骤,整理编制成完整的实验讲义. 实验步骤如下: 1)确定BBO晶体光轴方向、偏振片方向、半波片光轴方向以及激光偏振方向. 2)保证所有元件等高(以激光高度或BBO中心高度为标准). 3)调节激光器水平出光,全部光路平行光学平台. 4)利用自准直法调节四维镜架使凸透镜(f=500 mm)光轴与激光光线重合. 5)将主BBO中心放置在计算好的束腰聚焦位置,利用自准直法调节二维镜架使光线正入射BBO晶体. 粗调采用反打光方法,即利用光纤反向输入可见光来辅助确定光路中各元件的基本方位. 1)将反打光标记卡放在透镜与主BBO之间(计算好的位置). 2)调节五维光纤耦合器和反射镜,让反打光出射的红光聚焦在BBO晶体上的紫光束腰光点上,且红光光线中心能通过上一步的标记点. 3)放置其他光学元件,确保所有光学元件光心等高且自准直. 4)将光纤重新连接到单光子探测器上,通过细调光纤耦合器五维调整架实现单路光子计数最大,2路符合计数最高. 此时探测到的光子对处于纠缠态[式(5)]. 1)进行对比度测量:将偏振片θ1分别置于0°,45°,90°,135°,偏振片θ2在0°~360°内连续变化,测量符合计数,即可得出对比度曲线. 2)进行证伪Bell不等式的实验测量:θ1分别取0°和45°,θ2分别取22.5°和67.5°. 根据式(2)和式(6),测量单路强度N1,N2和2路符合计数N,计算S. 对于能力较强的学生,还设计了相关拓展实验内容: 3)其他Bell态的制备和测量. 4)密度矩阵测量:基于量子层析的思路对制备的纠缠态进行密度矩阵测量. 双光子纠缠实验系统作为实验教学仪器,已在北京大学物理学院开展了2个学期的本科教学实验,根据讲义,通过2次课8个学时基本都可实现教学目标,学生能够完成实验主要内容,部分能力较强的学生还开展了拓展实验. 在教学应用实践中,学生的数据结果基本都可达到以下指标:H,V(θ1=0°,90°)偏振对比度>25∶1;P,N(θ1=45°,135°)偏振对比度>10∶1. Bell不等式破坏程度较高(S>2.5). 下面选取一些实验数据进行分析. 当θ1分别置于0°,45°,90°,135°时,使θ2在0°~360°连续变化,记录对应的符合计数,得到对比度曲线如图5所示. 测量出最大和最小的符合计数,计算得到对比度,如表1所示. 图5 对比度曲线 表1 符合对比度 当θ1分别取0°和45°,θ2分别取22.5°和67.5°,利用符合系统可直接读出数据,如表2所示. 其中N1表示单位时间(1 s)内1路的光子计数,N2表示2路光子计数,N为两路光子的符合计数. δN为多次测量的平均偏差,E为关联函数值,最后由式(2)计算可以得到S.利用采集的数据,可计算得出此装置Bell态[式(5)]对应的S,S=2.551±0.025. 表2 Bell态的测量数据 在其中1路(或2路)辅助BBO和偏振片之间放置半波片,当半波片角度为0°时,该路上的H和V产生π的相位差. 当角度取45°时,可以使该路上的H和V互换,由此可制备出另外3种Bell态,即 (9) 表3 4种Bell态的测量结果 在2路辅助BBO和偏振片之间放置1/4波片,设偏振片透振方向分别是p1和p2,1/4波片方向分别是q1,q2. 对于偏振纠缠态[式(5)],除了基矢|H〉,|V〉外,通常还可以向斜45°线偏振与右旋/左旋圆偏振等基矢上投影,将这些基矢记作: 选择|H〉,|V〉,|D〉,|R〉作为投影的本征态,进行排列组合(需要进行16次测量).设系统密度矩阵的形式为 (10) 理想纠缠态[式(5)]的密度矩阵为 (11) 实验测量该系统纠缠态[式(5)]的密度矩阵结果如图6所示,计算出纯度Tr[ρ2]=0.81. (a)实部 (b)虚部图6 纠缠态[式(5)]密度矩阵的实验测量结果 (a)实部 (b)虚部图7 不加补偿时密度矩阵的实验测量结果 详细介绍了双光子纠缠实验教学系统的原理和在实验教学中的应用.搭建了双光子纠缠的实验系统,该系统可以直观展示量子纠缠概念、排除局域隐变量假设,系统稳定、可靠,实验难度适当.通过该实验,让学生直观深入地理解量子纠缠相关的抽象概念,通过搭建光路、调节光路及数据采集和分析,锻炼学生的动手能力和探索能力. 致谢:感谢本科生刘雨霖等同学在实验中的数据积累.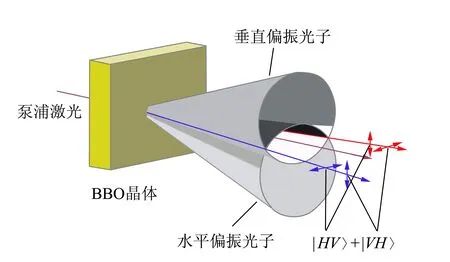
1.3 纠缠态的测量
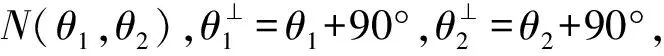
1.4 走离效应及补偿
2 系统结构及搭建



3 实验步骤及内容设计
3.1 初步搭建光路
3.2 光路的调节
3.3 数据采集和分析
4 实验结果分析
4.1 符合对比度测量

4.2 证伪Bell不等式
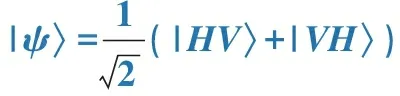

4.3 密度矩阵
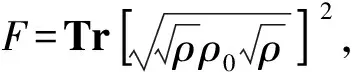
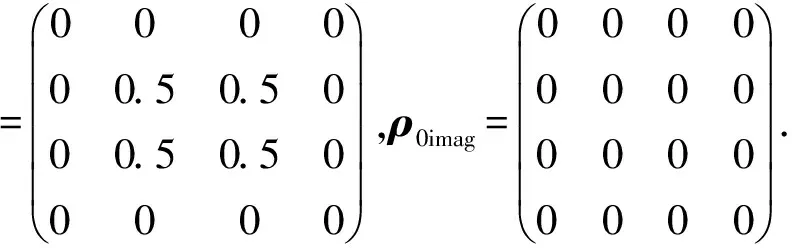
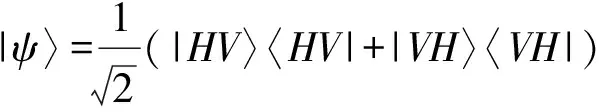
5 结束语

