基于空间分布规律的峰值跳变点去除仿真研究

杨先凤，张文俊，彭 博，李小兰

(西南石油大学计算机科学学院，四川 成都 610500)

1 引言

在超声弹性成像中，可以通过散斑追踪技术来估计软组织运动位移等信息。峰值跳变问题就是超声散斑运动追踪技术在计算位移时受到去相关因素干扰造成的。当回波信号去相关并且随机相关峰的幅度超过与正确散斑运动相对应的真实相关峰的幅度时，就会产生峰值跳变点。由于峰值跳变点的存在，超声散斑追踪得到的位移图像不够精确，对后期成像和医生诊断有较大的影响。

针对峰值跳变点的研究，目前主要集中在其运动估计算法上，如采用先验信息的区域增长算法[1]、贝叶斯算法以及采用位移正则化的GLUE算法[2]、提供子采样位移估计精度的Coupled[3]算法等。这些算法在去除峰值跳变点时均只针对某个单因素(如压缩比等)进行了去除研究，但未曾研究多种因素影响下产生的任意斑块半径峰值跳变点的去除。

经过对峰值跳变点分析研究，本文发现峰值跳变点与天文学星系中的点状物分布类似，而天文学中对点状物的分析常采用空间统计方法。因此，本文首次将空间统计方法-两点相关函数运用在峰值跳变点的研究中，找到如斑块半径等各因素影响下峰值跳变点规律；并分析比较多种峰值跳变点去除算法，结合得到的规律找到更优的去除方案。通过仿真分析峰值跳变点的空间统计规律，提出更优的峰值跳变点去除方案，为后续超声弹性成像中峰值跳变点的去除研究提供先验信息和参考依据。

2 峰值跳变点两点相关函数原理

相关函数计算可提供关于目标区域特定位置不同部分间相互影响的信息，对目标的空间统计特性进行分析。在d维欧几里得空间Rd中，峰值跳变图的N点相关函数由Torquato[4]定义为：

=〈I(i)(x1)I(i)(x2)I(i)(x3)…I(i)(xn)〉

(1)

上式中，〈 〉代表整体平均值计算，I(i)(x)为指标函数，定义如下

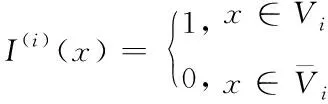
(2)

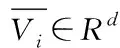
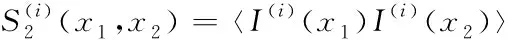
(3)

Berryman[5]提出了两点相关函数(2-pcf)的离散化版本，它可以从M×N大小的峰值跳变点矩阵估计S2(x为水平方向，y为垂直方向)。其计算公式如下所示

(4)

根据以上公式，Berryman引入附加等式

(5)

若方程中的值k(固定半径)和θ(角度)已知，则平均两点相关函数可以写成：

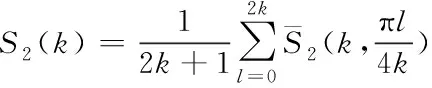
(6)

这里k是参数，小于或等于图像最小尺寸的一半。

但是，采用以上方程计算高分辨率峰值跳变图像时会出现运算时间过长或无解的情况。因此，Velasquez等人[6]提出一种简化的基于蒙特卡罗模拟的两点相关函数计算，其计算过程如图1所示。

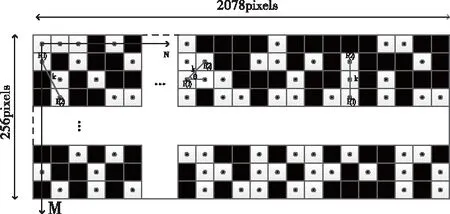
图1 两点相关函数计算示意图

上图中两点相关函数计算的主要步骤如下：

1) 随机生成点p1，θ角。

2) 以该θ角和固定长度k生成另一个随机点p2。

3) 分别计算两个随机生成的点都在峰值跳变点中的命中数，记为Nk-hits。

4) 根据如下所示的公式计算两点相关函数值为

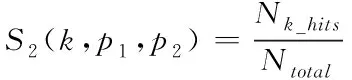
(7)

其中，Ntotal是每个长度k所计算的总数。根据Velasquez等人观察到Ntotal>10000在计算中可提供最可靠的结果，因此在k的每个值处设置Ntotal=100000用于计算。

3 峰值跳变点优化分析研究

本文使用了三类数据进行两点相关函数仿真分析和各去除算法对比分析，分别为计算机模拟数据、仿组织体模数据及真实乳腺超声数据。通过快速归一化互相关算法(NCC)[7-9]对压缩前后的RF回波信号进行运动位移估计，得到带有峰值跳变点的位移估计图。

3.1 峰值跳变分析数据获取

对于计算机模拟数据，先在软件中进行组织体模的构建，然后利用有限元求解器，获取局部组织变形的真实位移信息，再通过其变形前后的RF信号来估计组织变形的位移信息。

这里列举各影响因素下计算机模拟数据在快速归一化互相关算法下产生的峰值跳变点图，如图2所示。

图2 模拟数据轴向位移图和峰值跳变点

图2(a-f)分别展示了在互相关追踪窗口尺寸为61*11、弹性模量为6000、简单模型和复杂模型、探头中心频率为7MHz、压缩比为2%时的轴向位移估计图，(a1-f1)表示对应的峰值跳变点，黑色表示估计误差小的正确像素点，白色表示估计误差大的峰值跳变点。从图中可以看出同一模型在不同因素下的峰值跳变点具有较大差距，故本文对各因素做两点相关函数分析。

对于仿组织体模数据，采用凝胶仿组织体模进行采集。体模大小为10cm*10cm，其内部有一个半径为10mm的球形包含物，球形目标的弹性模量是背景组织的四倍。该模型的射频回波信号使用Siemens SONOLINE AntaresTM采集，并使用40MHz的多行线性阵列换能器(VFX9-4)采样，组织形变是手动压缩造成的。真实乳腺超声数据是从人体乳腺病变超声数据库中任意选取的一组真实乳腺病变超声回波数据。

快速归一化互相关算法下仿组织体模数据和真实乳腺超声数据产生的峰值跳变点如图3-4所示，左边是轴向位移图，右边是对应的峰值跳变图。可以看出仿组织体模中峰值跳变点较少，真实乳腺数据峰值跳变图中存在大量呈斑块状的峰值跳变点。

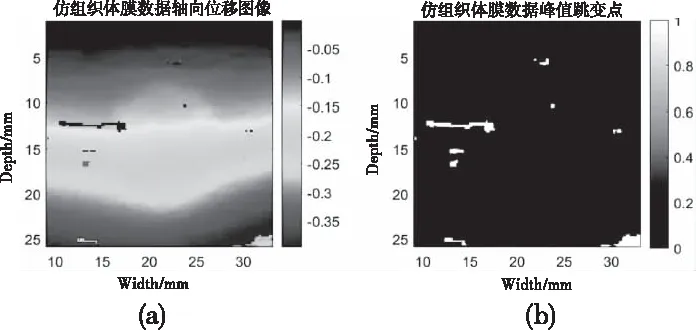
图3 仿组织体模轴向位移图及峰值跳变点

图4 真实乳腺数据轴向位移图及峰值跳变点

3.2 两点相关函数分析研究

在得到带有峰值跳变点的组织位移估计应变图后，将图中正确位移估计点和峰值跳变点看作两种异质材料，带入两点相关函数进行计算。表1列举了在图2中随机选取距离为1个像素(k=1)的两个点，经过两点相关函数计算得到的值。

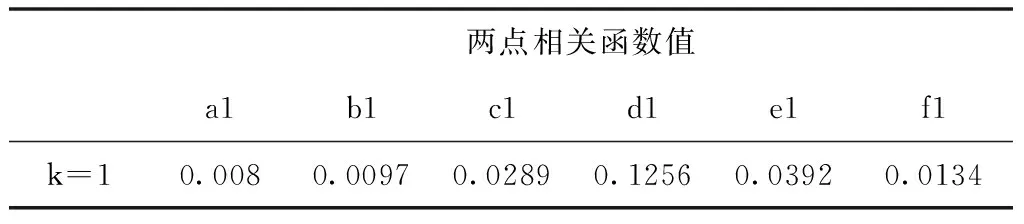
表1 k=1时两点相关函数值

结合图2和表1发现，图中峰值跳变点越密集，对应的两点相关函数值越大。

3.2 峰值跳变点去除方案研究

为了找到在各因素影响下更优的峰值跳变点去除算法，本文对目前已有的五种去除算法进行了实现，包括联合互相关和中值滤波(NCCM)算法、快速混合散斑跟踪(Hybrid)算法[10]、联合区域增长贝叶斯(RGBMT)算法[1]、GLUE算法[2]以及Coupled算法[3]。对每种算法采用客观评价指标加权比噪声比(简称加权CNR)评价，其计算公式如下：

(8)

STG和SBK分别是目标区域和背景区域的平均应变，σTG和σBK为目标方差和背景方差。CNR由目标wTG和背景wBK的相对总面积的比值贡献加权，二者总和为1。对于二维模型的信噪比，选择整个二维包含物作为目标，其余的跟踪ROI(感兴趣区域)为背景。使用加权CNR值可以描述各算法提高弹性应变图对比度的效果，值越大，去除峰值跳变点后生成的弹性应变图越精确。

计算出每个算法的加权CNR值后，结合前面小节中两点相关函数的分析结果，找到针对某种情况下去除峰值跳变点的优化方案。

有助于解决“城市热岛效应”，维护城市生态平衡。透水混凝土能够减少环境中的热量，有助于解决“城市热岛效应”。由于浅色和蜂窝状的结构，使其既不吸收热量，也不储存热量，也就不会将辐射的热量返回到大气中，从而减少环境中加热。雨水可通过透水混凝土迅速渗透下去，还原地下水，使大地恢复自然的储水能力，防止地下水枯竭，改善植被的生存环境，恢复地表的水循环系统，营造高质量的自然生态环境，维护城市生态平衡。

4 峰值跳变点仿真研究

软件实验环境包括MATLAB R2016b，ANSYS和Field II。为了方便观察，本文将峰值跳变点通过一定阈值从位移图中摘取出来。

4.1 计算机模拟数据两点相关函数仿真

通过ANSYS软件，对模型具体参数(互相关算法追踪匹配窗口尺寸、弹性模量、模型复杂度、探头中心频率、压缩比)进行设置，并计算两点相关函数值，结果如图5所示。

图5中三角曲线代表该因素影响下的最佳参数值，进行综合分析可得：五组因素下对应k值增大，峰值跳变点总体呈下降趋势；追踪窗口最优参数为101*11，大量的斑块半径(即k)为5，其余尺寸下为20；探头中心频率最佳参数为7MHz，大量斑块半径为9；越简单病变组织位移估计后峰值跳变点越少，大量斑块半径为16；组织材料因素下，大量斑块半径接近10且峰值跳变点较少。

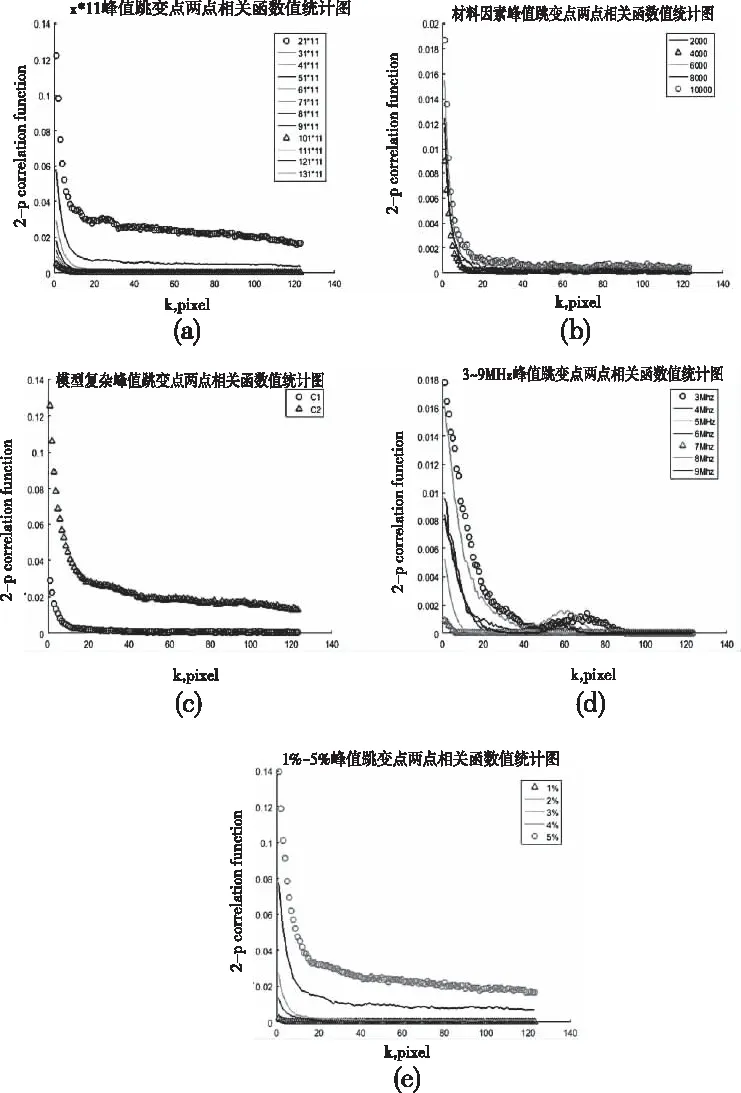
图5 计算机模拟数据两点相关函数曲线

4.2 仿组织体模数据两点相关函数仿真

仿组织体模数据两点相关函数计算结果如图6所示。在k=1处两点相关函数值为0.0143，对应图3中产生峰值跳变点较少。曲线从k=80时相关值逐渐接近于0，说明该仿组织体模数据产生的峰值跳变点斑块虽然大，但不连续。

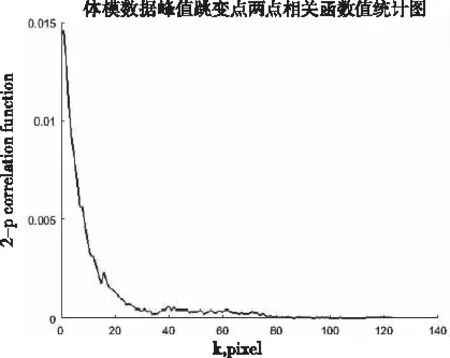
图6 仿组织体模数据两点相关函数曲线

4.3 真实乳腺数据两点相关函数仿真

真实乳腺超声数据的两点相关函数值如图7所示。

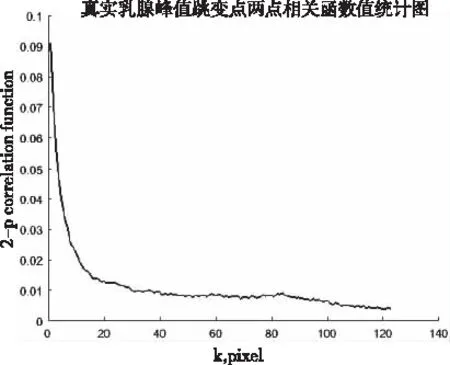
图7 真实乳腺数据两点相关函数曲线

从图中结果来看，真实乳腺数据在k=1处两点相关函数值为0.0926，对应于图4中峰值跳变点多且连续复杂。在k值逼近26个像素后两点相关函数曲线斜率降低，该数据产生的峰值跳变点成块状后，大部分斑块半径趋近于26个像素。峰值跳变点斑块半径较大，图片上的斑块呈连续状态，位移估计图质量较差。

4.4 峰值跳变点去除算法对比仿真

峰值跳变点各去除算法结果应变图的加权CNR值如表2-7所示，其中表2-5为计算机模拟数据。加权CNR值越大，则说明去除峰值跳变点后生成的弹性应变图越准确。

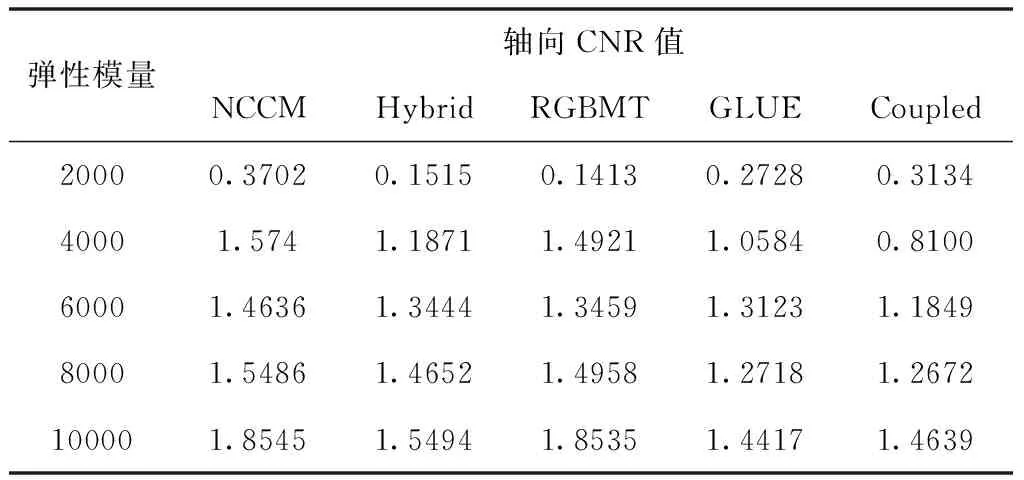
表2 组织材料各算法加权CNR值

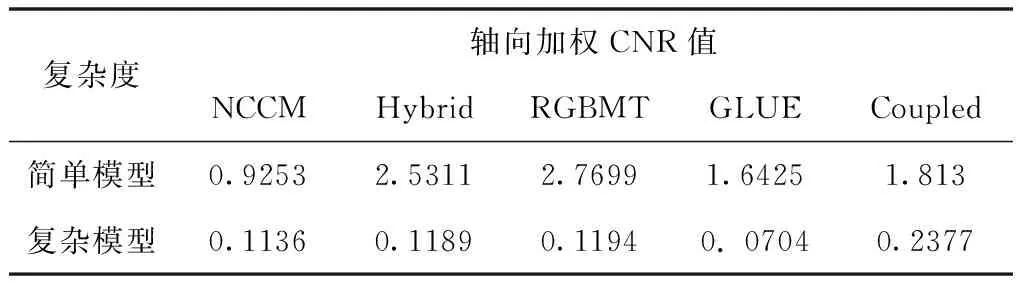
表3 模型复杂度各算法加权CNR值

表4 探头中心频率各算法加权CNR值

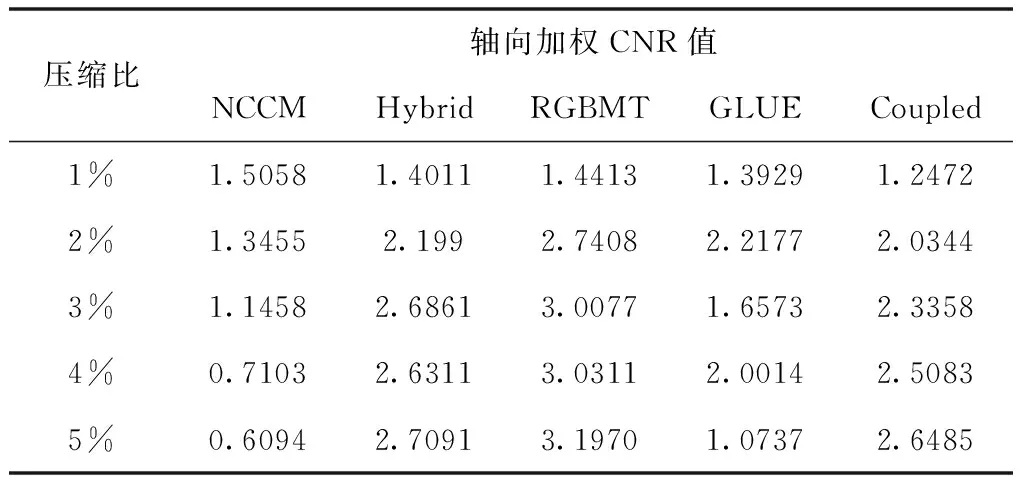
表5 压缩百分比各算法加权CNR值

表6 仿组织体模数据各算法加权CNR值

表7 真实乳腺数据各算法加权CNR值

经过两点相关函数仿真可得到某种因素下采用对应参数设置将会产生更好的位移估计，结合表2-7得出针对峰值跳变点多因素影响下的去除方案：计算机模拟数据中，在组织材料因素影响下且斑块半径≤10的峰值跳变点使用NCCM算法进行去除所获得的弹性应变图更精确；在模型复杂度因素影响下且斑块半径≥10使用RGBMT算法所获得的弹性应变图效果最优；在探头因素影响下使用RGBMT算法效果最优；压缩比因素影响下，当压缩比≤1%时使用NCCM算法效果最优，当压缩比≥1%时使用RGBMT算法效果最优。仿组织体模数据和真实乳腺数据中，处理半径较大且不连续的峰值跳变点斑块时，选择RGBMT算法能够获得较好的位移估计结果和应变图像。

5 结论

本文主要对超声散斑运动追踪中峰值跳变点的分布规律及其去除算法进行研究。首次将天文学中常用的两点相关函数(2-pcf)运用在峰值跳变点影响因素分析上，并对不同去除算法进行仿真比较。最后将比较的结果和空间分布规律结合在一起，提出了一种具有针对性的峰值跳变点去除方案。这些研究结果可为今后的峰值跳变点研究及去除算法的改进提供参考信息，具有一定的借鉴意义。