基于模糊PD控制的柔性航天器振动抑制研究

支敬德，戈新生

(1. 北京信息科技大学自动化学院，北京 100192；2. 北京信息科技大学机电工程学院，北京，100192)

1 引言

近年来，随着航天科学技术的不断发展，航天任务变得比以往更加复杂，对航天器的要求也逐渐提高，因此目前航天器系统大都带有柔性附件。考虑到航天器运载能力的限制，柔性附件通常选择质量轻、有一定柔性的结构，因此在航天器完成诸如机动、转向和空中对接等动作时，在姿态控制过程中执行机构输出的控制力会很容易激起柔性结构的振动，激发柔性附件的各阶模态，导致航天器的姿态失稳。因此，单纯的姿态控制已经不能满足高精度任务的需求，如何设计一种既能完成航天器姿态机动任务又能抑制柔性附件振动的控制律就显得至关重要。

在工程实际中，比例微分(Proportion Derivative， PD)控制，是一种应用十分广泛的控制方法。PD控制器简单易懂，使用中不需精确的系统模型等先决条件，正是这种特性使得PD控制方法在航天器姿态控制领域得到了广泛的应用。段柳成等[1]针对太阳翼的展开过程进行了研究和推导，并与ADAMS软件进行了对比，验证了其正确性，在控制方法中设计了一种基于位形本体信息反馈的PD控制方法，有效抑制了太阳翼展开过程中由关节摩擦引起的航天器位形漂移。Hua Liu等[2]研究了挠性航天器姿态控制问题，提出了一种基于扰动观测器的弹性振动前馈补偿控制方法，设计了由DOBC和PD控制相结合的复合控制器，有效减小了扰动，提高鲁棒动态性能。刘新建等[3]提出了一种PDA控制方法，即在PD方法基础上引入了航天器的刚性姿态加速度反馈，能够快速抑制低频大挠性系统中帆板的振动。殷春武等[4]针对太阳帆板展开过程中航天器姿态跟踪控制时系统以及外部干扰的不确定性问题，设计了姿态跟踪自适应动态比例微分(PD)控制器，能够实现航天器姿态机动，具有良好的鲁棒性。钟丽[5]改进了传统的刚体航天器定常PD+姿态控制律，将其和模糊控制，自适应控制，滑模变结构控制相结合，设计了全局滑模姿态控制律，增强了系统的鲁棒性。胡敏等[6]构建了一种刚体航天器姿态控制半实物仿真系统，在系统的数据通讯中采用了自组织网络，提高了航天器的灵活性，设计了比例微分控制器对航天器姿态机动进行控制。靳立强等[7]针对电动轮汽车动力学控制系统提出了一种最优PD控制方法，用最优控制对PD控制器增益进行整定，提高了系统的稳定性。宋锋[8]对PID自整定技术进行了研究，提出了一种优化的BP神经网络的PID自整定控制算法。张恒浩等[9]针对在挠性航天器系统中采用滑模变结构控制时控制力矩的抖振问题，将滑模变结构控制与模糊控制相结合，提出一种模糊滑模控制算法，消除了航天器姿态机动控制力矩的高频抖振问题。刘福才等[10]针对挠性航天器姿态机动过程中挠性结构的振动问题，提出一种模糊自抗扰控制方法，采用模糊算法对自抗扰控制器的参数进行整定，有效抑制了挠性航天器姿态机动时的振动。朱庆华等[11]针对滑模变结构控制器中存在的抖振问题进行改进，设计了一种动态滑模控制律，实现了对系统抖振的抑制，具有良好的控制性能。郑彦琴、戈新生[12]研究了欠驱动刚体航天器的姿态稳定性问题，对欠驱动刚体航天器进行运动学和动力学建模，设计了一种基于退步控制方法设计辅助变量的控制律，并与时不变控制律进行比较，证明了时变控制律的有效性。本文采用非约束模态法对柔性航天器构建适合控制器设计的状态空间模型，针对施加在柔性航天器上的PD控制所存在的姿态机动初始阶段控制力矩和姿态角速度过大所引起的柔性附件振动问题，在原有的PD控制基础上进行改进，引入了模糊控制，设计了一种模糊PD控制律。

2 柔性航天器模型

柔性航天器系统由主刚体带单侧太阳帆板组成，假设该系统由半径为b的中心刚体和长度为l均匀悬臂梁式柔性附件构成，系统的姿态运动方程和柔性附件振动方程为[13]

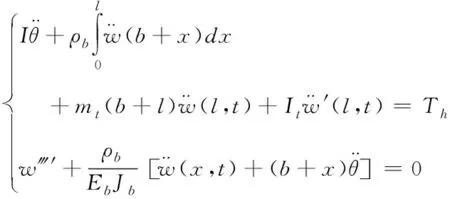
(1)

其中：I为系统总的转动惯量，Th为驱动力矩，ρb为梁的线密度，w(x，t)为梁上任意点x∈[0，l]相对坐标系的变形，mt为尖端质量的质量，It为尖端质量的转动惯量，EbJb为梁的抗弯刚度，θ为航天器的姿态角，“·”表示变量对时间t的导数，“′”表示变量对x的偏导数。

柔性结构离散化的主要方法有约束模态和非约束模态两种。约束模态定义为中心刚体固定，柔性附件无阻尼自由振动，在这种情况下体现的是柔性附件的固有特性；非约束模态定义为中心刚体不固定，柔性附件无阻尼自由振动，并且整个系统(中心刚体和柔性附件)都允许振动，在这种情况下体现的是航天器动力学系统频率特性。本文采用非约束模态方法将柔性结构离散化。由非约束模态的定义，将系统姿态运动方程和柔性附件振动方程写为

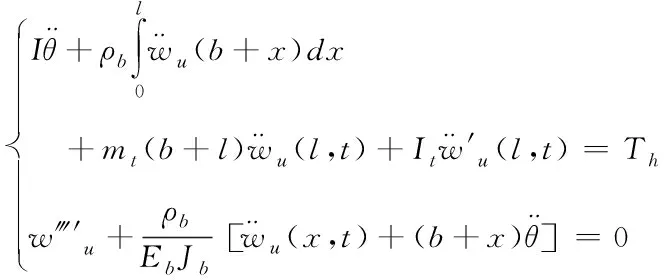
(2)

式中下标“u”表示非约束模态。

将非约束模态的解表示为仅依赖于空间变量的函数φ(x)和仅依赖于时间变量的函数η(t)的乘积，并将下标“u”省略，则有

w(x，t)=φ(x)η(t)

(3)

其中，φ(x)为柔性梁的第i阶振型函数。而由于模态是一个多值解，而线性方程式又符合叠加原理，所以式(3)的解为

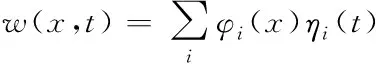
(4)

将柔性振动位移w(x，t)表示为振型函数φi(x)与模态坐标ηi(t)乘积的无穷级数和的形式，令

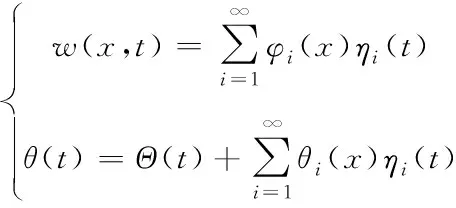
(5)

其中，Θ(t)是一个新引进的变量，其物理意义为假设柔性附件为刚体时卫星的姿态角，其引入目的是使变量变换后新变量数目和原变量相等。

将式(5)代入式(1)，将代入后的第二式两侧同乘φi(x)dx后对x自0到l积分，并应用模态正交性条件[13]，有

(6)

其中，η为柔性附件的振动模态坐标，ω为柔性结构的振动频率，f为柔性结构的耦合系数，且有fi=ti/I。

因此，采用非约束模态级数方法离散化得到的解耦后的航天器系统姿态运动方程和柔性附件振动方程可简化为

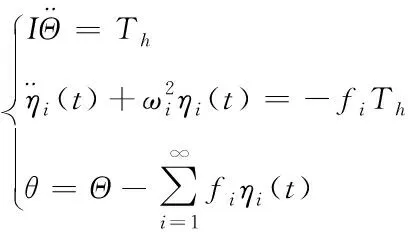
(7)

3 控制器设计

3.1 PD控制器设计

根据柔性航天器姿态角误差和误差变化率设计控制律为

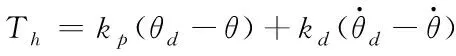
(8)

其中：θd为系统期望姿态角，kp和kd分别为PD控制的比例系数和微分系数。考虑到比例系数kp和微分系数kd在取不同数值时对于系统的调节时间影响很大，而调节时间过长，会影响柔性航天器的控制性能，所以必须在保证稳态误差精度的情况下尽量减小调节时间，使得系统的控制性能达到最佳。因此本文研究了比例系数和微分系数不同时对柔性航天器系统的影响。

3.2 模糊PD控制器设计

考虑到当给柔性航天器系统施加PD控制时，在保证稳态精度的情况下，航天器的初始时刻角速度过大，这会导致航天器的姿态失稳，而这主要是比例系数kp和微分系数kd是常数所引起的问题。因为kp越大，系统调节时间越短，但初始时刻角速度越大，kp越小，初始时刻角速度越小，但系统调节时间越长；而kd越小，调节时间越短，但初始时刻角速度越大，kd越大，初始时刻角速度越小，但系统调节时间越长。针对上述问题，在控制律设计中引入模糊控制，对比例系数和微分系数进行改进，使得航天器姿态机动的初始阶段kp较小，kd较大，随着时间的变化，kp逐渐增大，kd逐渐减小，使得系统更快达到稳定状态。引入模糊控制之后，虽然增大了调节时间，但大大减小了初始时刻航天器的角速度，使得系统更加平稳，保证了航天器的姿态稳定。

令姿态角误差为Δθ，则Δθ=θd-θ，根据2.1节中的PD控制律和系统响应结果，设计以下两条模糊规则

IfΔθ减小，则kd减小，kp增大

IfΔθ增大，则kd增大，kp减小

由这两条模糊规则可以设计出模糊控制系统，其中Δθ为输入，比例系数kd和微分系数kp为输出。定义系统的输入/输出模糊集如下

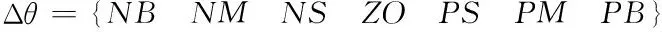
图1 模糊控制系统的输入/输出隶属度函数

其中，NB为负大，NM为负中，NS为负小，ZO为零，PS为正小，PM为正中，PB为正大。

设计模糊控制系统的输入/输出隶属度函数如图1所示。并设计如下七条模糊规则

IfΔθisPBTHENkdisPB，kpisNB

IfΔθisPMTHENkdisPM，kpisNM

IfΔθisPSTHENkdisPS，kpisNS

IfΔθisZOTHENkdisZO，kpisZO

IfΔθisNSTHENkdisNS，kpisPS

IfΔθisNMTHENkdisNM，kpisPM

IfΔθisNBTHENkdisNB，kpisPB

最后，根据当前Δθ的值，得到模糊输出kd和kp，采用重心法进行去模糊化，得到比例系数和微分系数的精确值d和p，则结合模糊控制所设计的控制律为

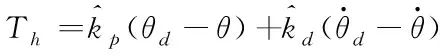
(9)

4 数值仿真分析

根据上文所设计的控制律，分别对PD控制和模糊PD控制进行MATALAB仿真，验证控制方法的有效性。

柔性航天器本体转动惯量(kg·m2)为[13]

I=26.0378

航天器本体与柔性附件之间的刚柔耦合系数(kg1/2·m)为

柔性附件的振动频率(rad/s)为

假定初始姿态角为0°，初始姿态角速度为0(°/s)，期望姿态角为60°，期望姿态角速度为0(°/s)，仿真时间为100s，仿真步长为0.01s。将式(8)和式(9)中所设计的两种控制律分别施加到柔性航天器动力学方程(7)中，代入给定参数，忽略柔性附件阻尼和扰动，分别对姿态运动方程和柔性附件振动方程进行求解，并用MATLAB数值仿真软件画出图像。PD控制仿真结果如图2、图3和图4所示，改进后的模糊PD控制仿真结果如图5所示，(a)、(b)、(c)、(d)分别为姿态角、姿态角速度、控制力矩和柔性附件振动模态随时间t变化的图像。

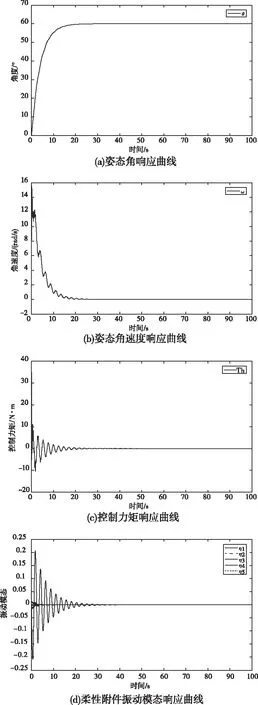
图2 kd=300，kp=75时PD控制仿真结果

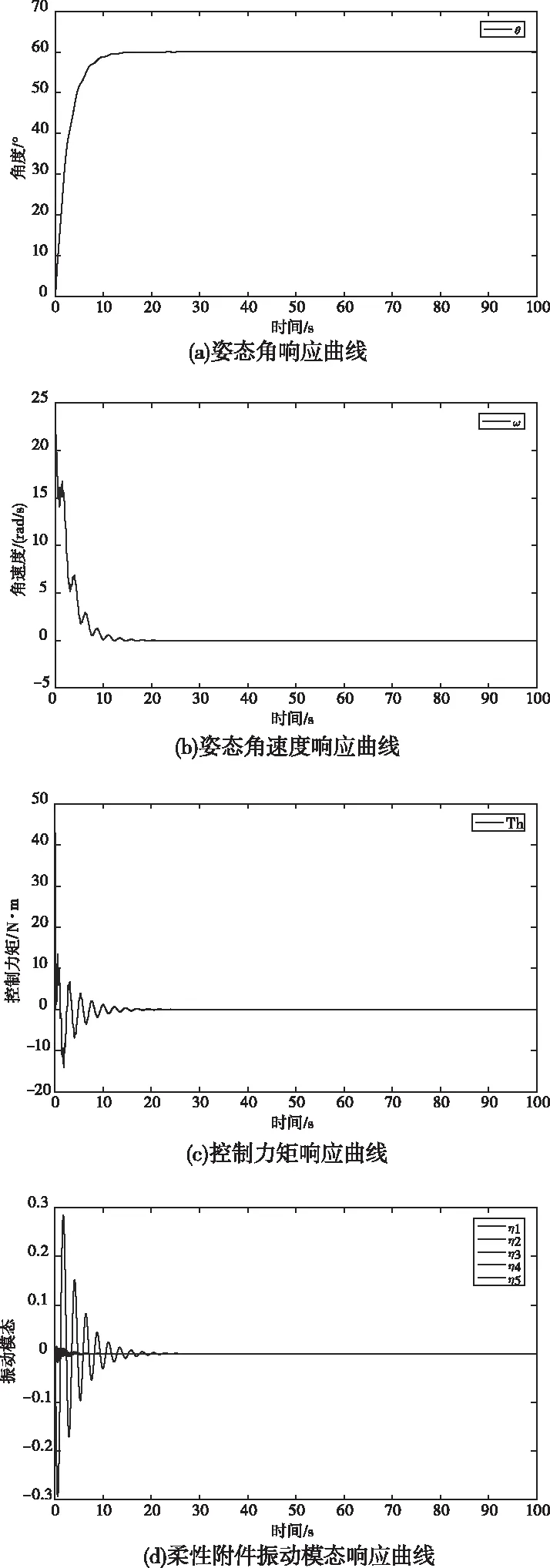
图3 kd=200，kp=75时PD控制仿真结果

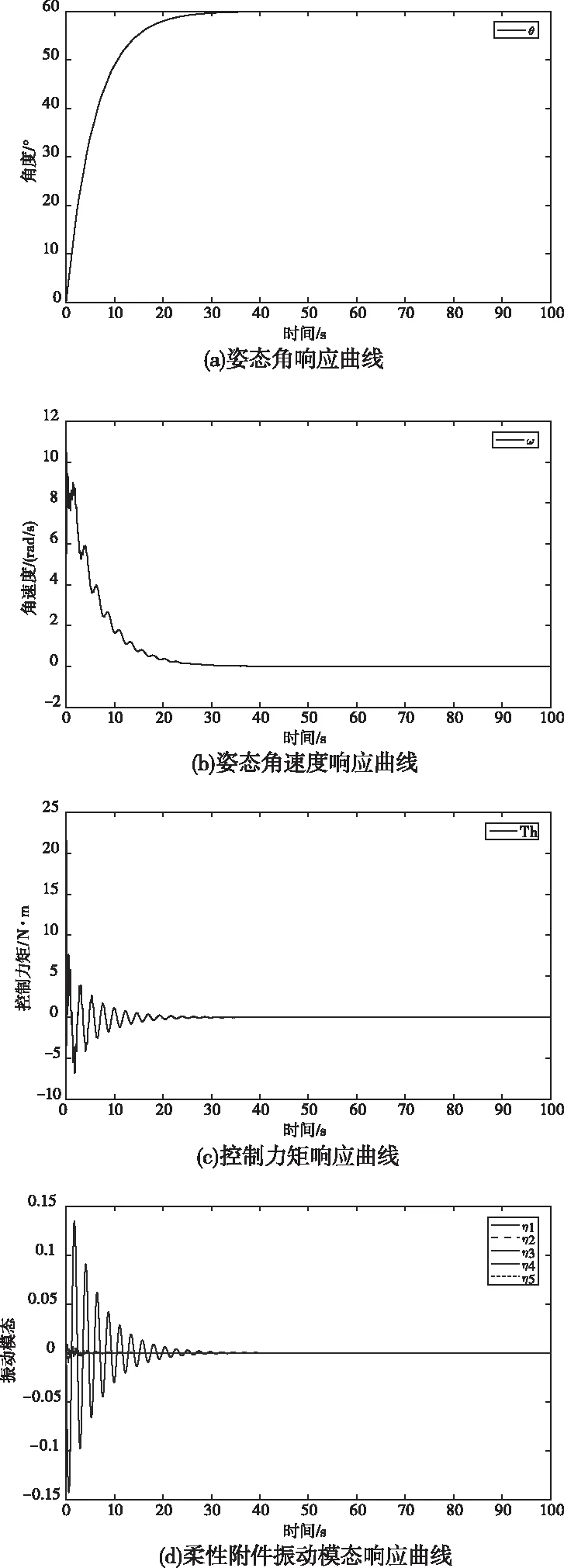
图4 kd=300，kp=50时PD控制仿真结果

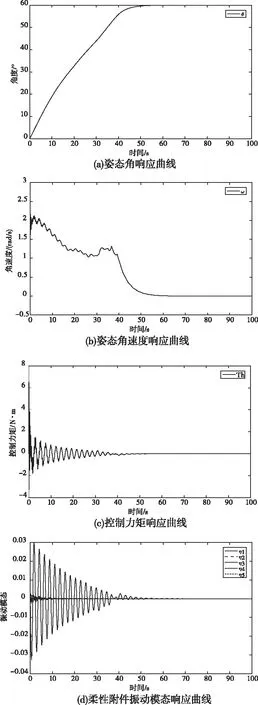
图5 模糊PD控制仿真结果

对比图2-图4可以发现，随着kp增大或kd减小，航天器姿态能较快收敛到期望角度，调节时间短，但控制力矩、姿态角速度以及柔性附件振动幅值增大；反之kp越小或者kd越大，收敛越慢，调节时间增长，但控制力矩、姿态角速度以及柔性附件振动模态较小。对比图2和图5可以发现，加入模糊控制之后，虽然调节时间变长，但能够大大减小初始阶段的控制力矩、姿态角速度以及柔性附件振动模态，能够使得柔性航天器在姿态机动时更加平稳，而在系统进入相对稳定阶段之后，kd接近300，kp接近75，又恢复到了原本的PD控制，并不影响系统的稳定性能。

5 结论

本文对柔性航天器姿态机动问题进行了研究，针对柔性航天器初始阶段的姿态机动角速度过大问题，在原有的PD控制基础上加入了模糊控制。通过对比取不同的比例系数和微分系数值时柔性航天器姿态机动过程，来分析比例系数和微分系数对控制系统的影响。在此基础上，针对初始阶段输出力矩和姿态角速度过大而容易引起柔性附件振动的情况，在控制律中加入了模糊控制，减小了控制力矩，柔化了控制量，解决了恒增益PD控制初始阶段姿态误差较高时控制力矩和姿态角速度过大的问题。本文通过MATLAB进行仿真，并对不同控制律作用下的响应曲线进行分析，验证了所提出的控制方法的有效性。仿真结果表明：改进后的控制律不仅能够实现柔性航天器的姿态机动，还能够对柔性附件的振动起到良好的抑制作用，提高了系统的控制精度，有效改进了PD控制所存在的问题。