基于法矢量雅可比的总广义变差图像修复模型

翟 艳，潘振宽，魏伟波

(青岛大学计算机科学技术学院，山东 青岛 266071)

1 引言

图像修复又称图像修补、图像补全、图像插值，是图像处理的最基本问题之一[1]。变分方法是图像处理、图像分析的重要方法，可有效实现图像修复、分割、重建等[2-4]。图像修复是根据图像中存在的信息恢复出破损图像丢失的信息，其变分模型[5]通常借助预先定义的掩模函数标记破损区域以构造能量泛函，利用图像扩散机制[6]将已有的图像信息扩散到破损区域，能量泛函中的规则项决定着恢复后图像的质量[7-8]。

针对小破损非纹理图像的修复问题，Chan等[9]将经典的总变差模型(TV， Total Variation)推广为变分图像修复模型，该模型继承了TV模型的边缘保持特点，但也使得恢复后的图像呈现阶梯效应。自然的改进方法是引入高阶导数的变分模型，如Chan 等[10]提出的基于曲率驱动扩散(Curvature-Driven Diffusions，CDD)的高阶变分模型，和基于欧拉弹性能(Euler’s Elastica，EE)的图像修复变分模型[11-12]。Lysaker等[13]则提出了基于Bounded Hessian (BH)的二阶变分模型可同时保持图像边缘与光滑特征，可用于图像噪声去除[14]及图像修复[15]。作为对BH模型的拓展，Bredies、Kunisch和Pock[16]提出了总广义变差变分模型(Total Generalized Variation，TGV)，进一步提高了恢复图像质量，并应用于大破损图像的修复[17]。

TGV模型以Hessian矩阵为基础，该矩阵是梯度的雅可比矩阵。本文拟将TGV模型的Hessian矩阵修改为单位法矢量的雅可比矩阵，使得图像边缘处扩散系数接近零，从而达到图像光滑与边缘的同时保持的目的。为此，本文在分析BH模型和TGV模型[18]基础上提出了基于单位法矢量雅可比的总广义变差图像修复模型(Total Generalized Variation Based on Jacobian of Normal，TGVJN)来提升大破损图像的修复精度。模型采用的交替方向乘子法是求解具有可分结构的凸优化问题的重要方法，近年来大量应用在数据分析处理领域。通过引入多个辅助变量、拉格朗日乘子及惩罚参数设计相应的交替方向乘子法(ADMM， Alternating Direction Method of Multipliers)实现模型快速求解。最后，对所提出模型进行一系列数值实验来验证其图像修复效果。

2 相关研究工作基础

2.1 BH模型

BH模型利用图像强度Hessian矩阵的Frobenius范数对图像进行去噪或修复处理。该模型的能量泛函可以写成如下形式

(1)

其中f代表输入的图像，u代表恢复后的图像，α是惩罚参数，且必须满足条件α>0。对于二维图像，采用dx来代表dx1dx2，图像强度u的Hessian矩阵为

∇(∇u)

(2)

2.2 TGV模型

总广义变差模型的二阶规则项形式为

(3)

(4)

总广义变差模型可以推广应用于图像修复等方面，该模型利用破损区域的边缘信息沿梯度方向扩散对破损区域内部进行修复[19]。二阶TGV修复模型的能量泛函极值问题为

(5)

∇为梯度算子，α，β是惩罚参数。该能量泛函中的第二项和第三项分别作为一阶和二阶规范，这使得模型具有良好的边缘保持特性和光滑性。

3 基于法矢量雅可比的总广义变差模型-TGVJN

(6)

α，β是两个惩罚参数，χD作为掩模函数用来标记破损区域。图像中破损区域D标记为0，非破损区域Ω/D标记为1 。考虑到高阶模型的计算复杂性，采用交替方向乘子法来提高计算效率，下面引入一些辅助变量对其进行求解

w=∇u

(7)

(8)

q=ε(p)

(9)

v=p-n

(10)

为了避免计算中直接使用约束(8)带来的复杂性，可将其松弛为如下格式

|w|-w·n≥0

(11)

通过引入拉格朗日乘子λ1，λ2，λ3，λ4和惩罚参数μ1，μ2，μ3，μ4，能量泛函可以写成増广拉格朗日泛函形式

(12)

在此基础上，通过设计交替方向乘子法来优化迭代方案，并将原泛函分解为一系列的最小化子问题。在每次循环迭代中，依次考虑变量u，p，w，n，q，v最小化问题。各变量依次迭代结束之后，拉格朗日乘子会进行更新

(13)

(14)

(15)

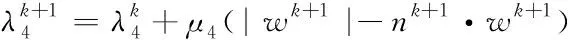
(16)

在交替求解变量的极小值过程中，变量u，p，n采用高斯-赛德尔迭代方法求解子问题得到对应的欧拉-拉格朗日方程，而w，v，q的子问题具有相同的格式，可以通过广义软阈值公式直接得到计算结果。

通过求解u的子问题，得到的欧拉-拉格朗日方程可以写成以下形式

(17)

计算变量w的子问题，采用广义软阈值公式可以得到如下形式的解

(18)

通过变分方法可以求解得到关于变量p的欧拉-拉格朗日方程

(19)

变量v，q可以分别通过广义软阈值公式计算得到，结果如下所示

(20)

(21)

由于变量n还需要满足约束|n|≤1，所以在得到欧拉-拉格朗日方程之后要对其进行一次投影来提高精确度

(22)

本文算法求解步骤如下：

输入：原始破损图像f

输出：修复图像u

1)初始化，将变量u，p，w，n，q，v值设为0，拉格朗日乘子λ1，λ2，λ3，λ4值设置为0，惩罚参数α，β，μ1，μ2，μ3，μ4>0。

2)在每步迭代中交替计算变量并更新拉格朗日乘子。

3)迭代直至满足收敛条件，得到u。

其算法流程图如图1所示。

图1 算法流程图

4 实验结果与分析

本文所有实验在PC(Intel Core i5-6500 CPU @3.20GHz，4.00GB内存)上完成，编程环境为 MATLAB R2016a。为了验证提出模型的有效性，下面将给出经典BH模型与TGV模型及本文改进的TGVJN模型的去噪及破损图像修复的实验对比，三种模型都采用交替方向乘子法设计实现。利用峰值信噪比(PSNR)、结构相似性指数(SSIM)和均方根误差(RMSE)三个参数对去噪和修复模型进行了客观的比较，其中PSNR和SSIM越高表明处理后的图像越接近原始图像，RMSE则相反。拐角、边缘保持及对比度等特性在下方实验中给出了详细展示。

在实验分析之前，先给出本文模型的主要参数取值范围。α，β是模型参数，范围约在：1-1000。其中α作为惩罚参数将当前项值近似为0，β约束模型中的规则项，控制图像扩散强度。μ1，μ2，μ3，μ4是算法设计中引入的惩罚参数，一般情况下需要设置较大的值，但实验分析后发现将其设置的过大容易弱化模型中其它项的影响。故在此模型设置惩罚参数μ1：1-100，μ2=1，μ3=1，μ4=0.1。

4.1 去噪实验结果与分析

图2直观地展示了各个模型保持分段常值图像的边缘效果。(a)是加入了0.01方差的高斯噪声图像，(d)，(f)和(h)是各模型去噪结果同原图的误差图。理想状态下误差图中不应该包含任何图像信息，这组实验直观展示了模型对图像对比度的保留能力。与其它两个模型相比，BH模型的去噪效果并不理想，且边缘模糊。(d)图条形边界处存在的竖线证明BH模型在去噪过程中会丢失一些边缘信息。(e)和(g)直观说明TGV模型和本文提出的TGVJN模型都能够有效的去除噪声且平滑效果显著，(f)和(h)的误差分析说明本文提出的TGVJN模型的误差图包含了较少的边缘信息和图像结构信息，验证了TGVJN模型在边缘保持方面更具有优势。

图3给出了图像的中间部分切线图和能量收敛图，该实验中添加0.005的高斯噪声。BH模型的去噪结果切线与原图切线整体贴合度较低且不平滑，TGV模型的去噪结果切线在跳变处平滑了拐角，侧面印证了该模型存在的边缘模糊现象。而本文提出的TGVJN模型去噪结果切线在跳变处保持了拐角与原图切线拟合较好。本实验将能量误差设定为0.001，能量收敛图展示了各模型的收敛速度。其中BH模型的收敛速度最慢，TGVJN模型比TGV模型收敛速度略快。表1比较了在图2 (b)中加入不同噪声方差后各模型去噪结果的参数。

图3 去噪结果中间切线及能量图

表1 去噪实验客观参数比较

4.2 大尺度破损修复实验结果与分析

图4(a)破损区域宽度为40像素点，分别用三种模型对其进行修复。BH模型不能完全修复好这样的大尺度破损，在图5 (a)局部放大图中破损区域中心与周围存在明显误差。TGV与TGVJN模型在非边界区域修复效果显著，但从图5中可以看出TGV模型在边界处的模糊区域较大，本文提出的TGVJN模型虽然不能完全复原出边界线但大大缩减了模糊区域。

图4 Bar图像修复结果对比

图5 图4 (b)-(d)的部分放大图

图6(a)破损区域宽度为20像素点，分别用三种模型对其修复处理，再将各模型结果图与原图做差得出误差图。BH模型在椭圆的破损边界处产生了明显的模糊区域，而TGV和TGVJN模型更好的修复出了椭圆边界。直观视觉上难以区分出哪个修复结果更加精确，但(d)，(f)误差图说明TGVJN模型修复结果误差较小，更加贴合原图。

图6 Circle修复结果和误差对比

4.3 小尺度破损修复实验结果与分析

图7(a)中添加了大面积的文字水印，该实验比较了三种模型对小尺度但大面积破损图像的修复能力。其中TGVJN模型表现最好，BH和TGV模型都不能完全修复破损区域，BH模型甚至出现了破损区域图像强度增强的问题。

图7 Turtle修复结果对比

图8(a)破损交叉处丢失信息较多， BH模型没有完全修复破损区域，图8(b)中出现了斑点，且在帽沿等边缘处边界不清晰，有模糊现象。在图9局部放大图中，TGV模型在头发等一些局部破损处不能修复完整，但BH模型和TGVJN模型包含的规则项具有增强线性结构的特性，在这方面优势明显。总体来说，TGVJN模型展现了更好的修复效果。最后表2中列出了三种模型修复实验的客观评价参数。

图8 Lena修复结果对比

图9 图8 (b)-(d)的部分放大图

表2 修复实验客观参数比较

5 结束语

为了复原更多的图像信息，提高图像修复的精度，本文提出了基于法矢量雅可比的总广义变差模型，并设计了相应的ADMM算法。通过对噪声图像设计去噪实验，对不同尺度破损图像进行修复实验，来对比本文提出的模型与之前的模型的去噪和修复效果及客观参数。去噪实验结果表明，本文提出的模型具有提升图像对比度、保持边缘清晰的性质。在修复实验中，相比于BH和TGV模型，本文模型能够更好地修复大尺度破损区域，同时可以兼顾图像中的线性结构和边界信息，减小边界模糊区域，提升了修复的精确度。本文模型采用ADMM方法求解，涉及到的参数较多，可以采用更加快速的求解算法来提升计算效率。今后可以将本文的模型应用于彩色图像修复和3维重建等方面的研究。