基于布谷鸟搜索算法的水质污染扩散仿真

唐林旺，李雪蓉，麻欣宇，王俊峰，2*

(1. 江西理工大学资源与环境工程学院，江西 赣州 341000；2.江西省矿冶环境污染控制重点实验室，江西 赣州 341000)

1 引言

水资源作为人类以及自然界中所有生物的生存根本，其用途广泛，无法代替，同时也最容易受到外界污染。水体污染会导致围绕水体生存的生态群体受到影响。且会导致污染所处区域的水文条件和污染物的种类、强度、时间、地点等各方面出现较强的不稳定性，且污染物随时处于变化的状态，随着水体的流动发生迁移难以掌控，会对环境、经济以及社会造成严重的破坏性，甚至甚至会通过生态链危害人类的身体健康[1-2]。

为此本文提出一种基于CS(Cuckoo Search)算法的水质污染垂向扩散跟踪建模方法，是基于布谷鸟的繁衍方式以及莱维飞行演变所得到的算法，因布谷鸟会把鸟蛋生在宿主鸟的巢内，若被宿主鸟发现，就会发生冲突，而宿主鸟事后发现布谷鸟蛋，那么会在其它地方建立一个鸟巢或者将其鸟蛋推出巢穴之外；而布谷鸟的蛋一旦被宿主鸟孵化，会将宿主鸟的蛋推出巢穴外，本文根据该特性，随机地输入数据，寻找最优二维水质水流模型，随后凭借计算横向系数，利用垂向系数观察污染物对于水体垂向污染的影响，完成最终的跟踪建模。

2 CS算法的应用计算原理

将CS算法做出三种理想假设，具体如下所示：

1)布谷鸟随机生产在某宿主鸟巢内；

2)布谷鸟蛋会被孵化。

3)布谷鸟能够使用到的宿主鸟巢穴个数n为固定的，而布谷鸟鸟蛋在宿主鸟巢穴内被发现概率为pa∈[0，1]。

以上述三种假设作为前提，可以得到布谷鸟寻找鸟巢的位置以及路径，具体公式为：

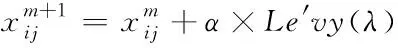
(1)

莱维飞行连续的跳跃路径和时间关系是服从莱维分布情况[3]，通过对分布函数进行简化以及傅里叶变换之后，获得幂次的行为概率密度函数，具体可得公式为：

Le′vy～u=t-λ；1<λ<3

(2)

上式中：λ代表幂次系数。

由于通过模拟莱维飞行的跳跃路径，可以获得具体公式为：

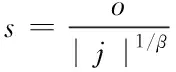
(3)

上式中：s代表莱维飞行跳跃的路径Le′vy；参数Le′vy(λ)与式(2)内λ关系是λ=1+β，β的取值范围是0<β<2，能够在CS算法内取β=1.5，参数o、j代表正态的分布随机数，可以服从式(4)正态的分布情况，在式(4)相应正态的分布标准差为σo、σj取值，具体如式(5)所示：

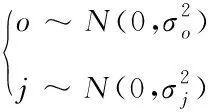
(4)

式中，

(5)

布谷鸟按照莱维飞行方式，其搜索路径是随意改变的，此时会从一个区域转换至另外一个区域，使其整体寻优的能力增强，此外，CS方法凭借布谷鸟的生存方式，能够对其进行定义，在布谷鸟被宿主鸟所发现的概率为pa=0.25，以此可以适应环境的布谷鸟则被孵化，反之，则会被淘汰掉，以此剩下最佳的布谷鸟。本文凭借CS方法的强收敛性对整体水域水流流动方式进行搜索，寻找最优的流动路径以后，通过构建污染跟踪模型，寻找出污染物的扩散情况[4]。

3 水质污染问题的垂向扩散跟踪建模方法。

3.1 水质污染垂向扩散系数

水质污染的垂向扩散系数是衡量污染物在河渠内运输能力的重要参数[5]，采用对流速分布的函数形式，以此能够在各向同性的紊动条件之下，得出污染物垂向扩散的系数。

以混合区域外边界的标准曲线特征尺度基础，获取顺直宽阔的水体垂向扩散系数，具体公式为：

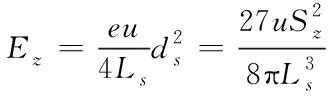
(6)

上式中：Ez代表垂向的扩散系数，单位为：m2/s，Ls代表河渠最大的宽度，单位为m，Sz代表河渠的垂直方向面积，单位为m2，e代表岸边污染混合区域的最大长度以及对应纵坐标比值。

在式(6)内表明，河渠的垂直方向平均流速u恒定条件下，垂直方向上面积Sz越大，说明垂向扩散的系数Ez就越大，而最大的长度Ls越大，那么垂向扩散的系数Ez就越小[6]。

3.2 二维污染物垂向跟踪模型

河渠的一维水流水质模型，一般情况下要对其进行理想化以及大量简化的操作，而实际过程内，要模拟水体种类有很大几率不满足一维模型的理想状态，例如：水平宽度较大或者水平尺度较短、横向浓度的梯度较大等问题，这时不用对水力水质参数沿着垂向变化进行考虑，可采用沿着水深均匀流动量来代表垂直方向流场，因此根据CS算法的应用原理，本文采用CS算法获取二维水流水质的模型，该模型能够跟踪水体内水流垂向与污染物浓度变化，从而完成跟踪建模[7]。

3.2.1 水动力模型

在河渠内获得从水底至水面微小的水体。h0、z0分别代表某一个基准面下河渠水位以及底部的高程，Ux、Uy、Uz分别代表x、y、z方向上沿着水深的平均流速，u、v、w分别代表x、y、z方向沿着水深时的平均流速，具体公式为：

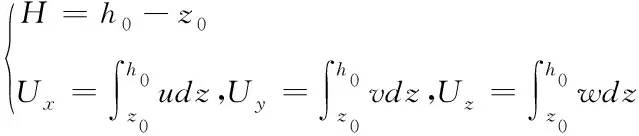
(7)

自由表面和底部的运动学条件公式为：

(8)

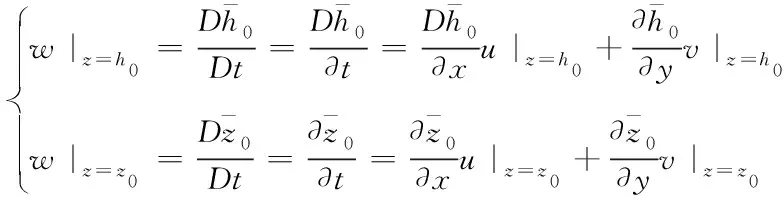
(9)

1)沿着水深均匀连续性的方程

水流的连续方程公式为：

(10)

上式中：q代表单位面积上污染物进出河渠流量，其中，流入即为正，而流出为负[8]。

2)沿着水深的平均运动方程

(11)

设定u、v分别代表河渠内x、y方向流速分量，那么河渠x方向动量的输运方程公式为：

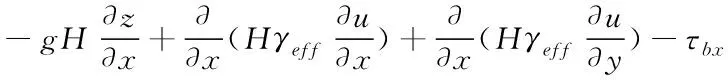
(12)

与河渠x方向动量的输运方程相似，河渠y方向上动量的输运方程公式为：

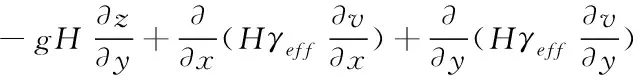
(13)

河渠湍流动能以及湍流耗散输运的方程公式为：

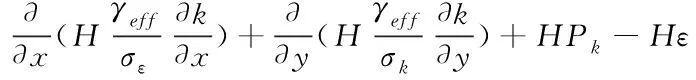
(14)

湍流动能的产生项公式为：

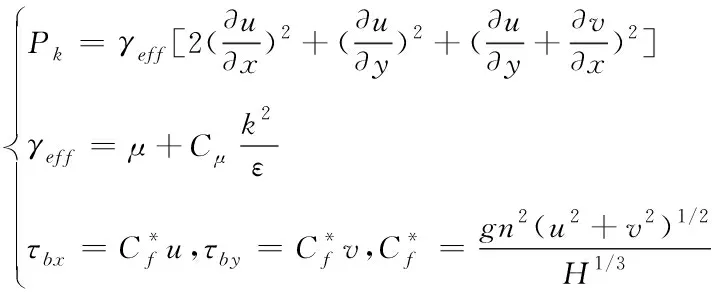
(15)

上式中：g代表重力的加速度，n代表河渠的底部糙率，k代表河渠的深度湍流动能，ε代表耗散率，μ、代表分子动力粘性的系数，μt代表漩涡运动粘性的系数，γeff代表有效的粘性系数，C代表河渠输送水质变量的浓度，单位是g/m3，SC代表污染物强度，Sk代表河渠内污染物的衰弱减项[9]。

3.2.2 污染物跟踪模型

污染物在进入水体内，会发生扩散，在任意的dt时间段中，所有因素一起作用，会引发微分单元体内的污染物质量增量，包括水平面(x，y)方向的变化量。因此要构建水体内污染物的输运微分方程，就需要许多因素一起作用下，所引发单元体积中，污染物的变化量与该水体中污染物处于dt时间段中的变化量[10]。

1)在水流的作用下，处于x、y方向所引发污染物的增量通量，具体公式为：

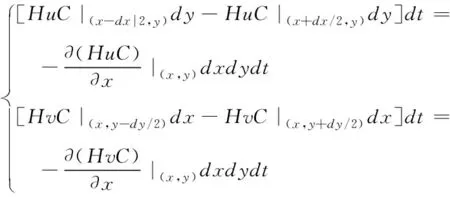
(16)

2)在分子的分散作用下，处于x、y方向所引发污染物的增量通量，具体公式为：

(17)

3)在紊动扩散作用下，处于x、y方向所引发污染物的增量通量[11]，具体公式为：

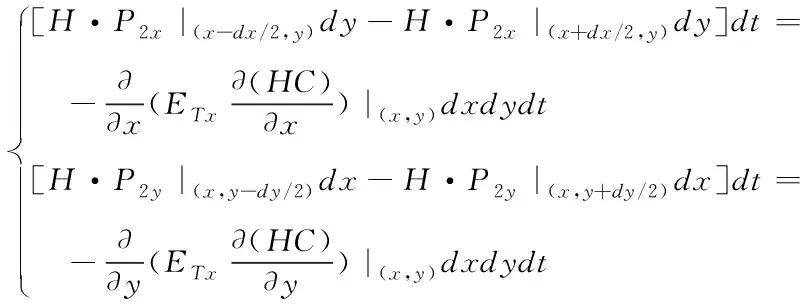
(18)

4)在弥散作用下，处于x、y方向所引发污染物的增量通量，具体公式为：

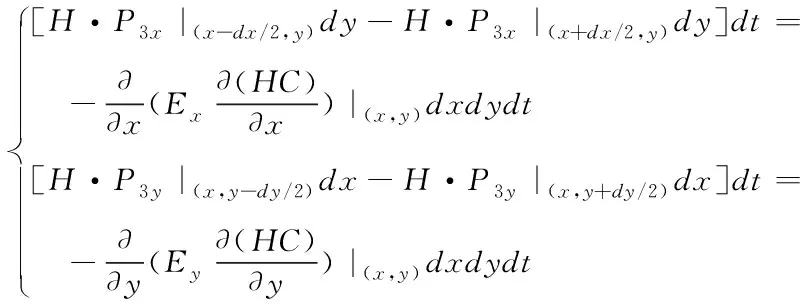
(19)

5)在微元体源项Sv和水体衰减作用下所引发污染物的增量通量，具体公式为：

Sv|(x，y)dxdydt+Sk|(x，y)dxdydt

(20)

依据质量守恒定律，获得河渠二维污染垂向跟踪的转换基本模型，具体公式为：

(21)

上式中：t代表污染物的运移时间，单位是h代表河渠跟踪高度，Ex、Ey分别代表河渠x，y方向上离散系数[12]，其单位为m2/s。

4 仿真实验设计

4.1 实验一

为验证本文方法的有效性，选择实验环境，如表1所示：

表1 实验环境

通过模拟测试，设定水面污染源的强度为：m=50g/m2，横向以及垂向系数分别为：0.1m2/s、0.02m2/s。扩散时间为t=1000s，水深20m，在该次实验分成三次进行，不考虑横向污染的影响，仅观察垂向污染扩散情况，具体结果如图1所示：

图1 模拟污染物垂向扩散系数

通过观察图1能够看出，分别进行三次不同的污染浓度测试过程中，第一次污染物浓度较低，当扩散至大约2米的位置，浓度扩散系数逐渐降低，而达到5米的位置，基本停止向下扩散，开始随着时间的流失，横向扩散，由于横向扩散跟踪系数，不在本文实验考虑范围之内，因此第一次终止；第二次提升污染物浓度为第一次的一倍，在几秒钟内，扩散得深度就超越了第一次，然后随着时间的推移，在约9米处扩散系数降低，由于该次浓度较大，直到扩散约12米处才基本停止向下扩散；第三次，再次提升一倍的污染物浓度，但污染物并没有像第二次以很快的速度超越第一次一样，超越第二次测试，而是在达到10米的时候，出现匀速下降，直到14米的时间，扩散系数降低；第四次浓度为12mg·L-1到15米的时候扩散系数降低，16米就已经停止扩散。总结来说，污染物浓度越大，垂直扩散越深，随着深度提升扩散系数会逐步降低，对污染物的影响力就越小。

4.2 实验二

为进一步验证本文方法的建模效果，通过实际污染扩散情况进行对比，在相同条件，观察二者之间垂向扩散的变化情况，具体如图2所示：

图2 本文跟踪结果与实际跟踪结果对比

通过观察图2能够看出，本文方法跟踪建模的模拟情况与实际污染扩散情况，它们的曲线波动，基本相同、差距较小，都是随着时间的增加，扩散的越深。这是由于本文通过CS算法可以找出水体流动的方式，再以污染物随着水体流动的方式，找出污染物的扩散系数，完成有效跟踪。

5 结束语

本文采用CS算法获取二维水流水质的模型，跟踪水体内水流垂向与污染物浓度变化，

根据混合区域外边界的标准曲线特征尺度获取流速分布函数计算水体垂向扩散系数。结合水体污染垂直方向上的流场，从而完成污染扩散跟踪。最后设计仿真实验，实验分为两部分。实验首先获取了模拟污染物垂向扩散系数，基于此结果，将模拟的实验结果与实际结果对比，二者之间的扩散系数基本相同，以此能够证明本文方法能够符合现实的精准跟踪需求。

不过本文并未考虑特殊的环境场所，例如，水流速度极快的河渠、携带沙土的河渠等，因此，未来本文还需要进一步研究，争取跟踪的范围更广，构建更精准的模型。