一道解三角形真题的多解与反思

山东省青岛经济技术开发区第四中学 王永刚

1 引言

每年的高考真题，总有众多的亮点，名题荟萃，创新新颖，典型突出，引入注目.此类高考真题，知识融合交汇考点明确，立意突出，科学创新，具有非常好的教学价值，吸引了众多命题者的引用、模仿与改编等，这些优良的创新“产品”经常出现在一些高考模拟卷中，值得我们细细品赏，好好深入分析与研究.

2 问题呈现

问题(2020届广东省广州市高三年级阶段训练题理科·16)已知△ABC的三个内角为A，B，C，且sinA，sinB，sinC成等差数列，则sin 2B+2cosB的最小值为______，最大值为______.

此题以三角形为载体，结合三角形的三内角的正弦值成等差数列来设置限制条件，进而求解角B所对应的三角关系式的最值.破解此题可分为两个步骤：(1)利用条件确定角B的取值范围；(2)在角B的限制条件下确定sin 2B+2cosB的最值.而对应两个步骤的切入思维多样，破解方法各异.

3 问题破解

(1)确定角B的取值范围.

方法1：(三角恒等变换)

由sinA，sinB，sinC成等差数列，可得sinA+sinC=2sinB.

结合三角恒等变换公式，可得

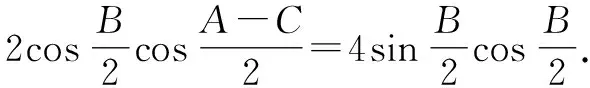
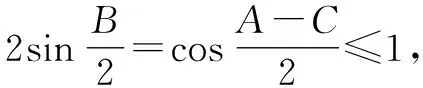
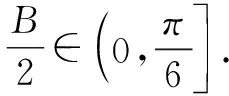
方法2：(基本不等式法)

由sinA，sinB，sinC成等差数列，可得sinA+sinC=2sinB.结合正弦定理，有a+c=2b.

由余弦定理，得

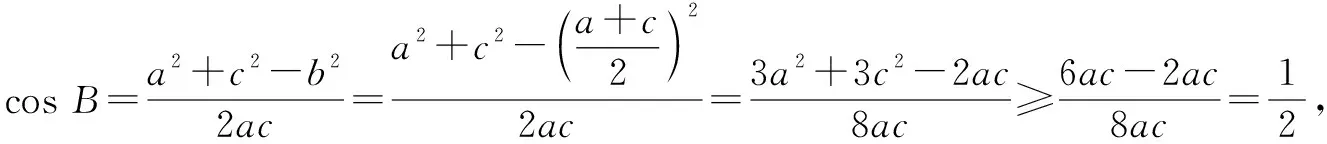
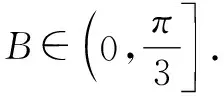
方法3：(椭圆模型法)

由sinA，sinB，sinC成等差数列，可得sinA+sinC=2sinB.结合正弦定理，有BC+BA=2AC.

不妨设AC=2，则BC+BA=2AC=4.

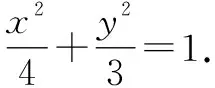
点评：根据题目条件，结合等差中项的应用得到关系式sinA+sinC=2sinB，直接通过三角恒等变换以及三角形的性质可以确定角B的取值范围，此方法对三角恒等变换公式的要求比较高；而常见的方法是由三角关系式借助正弦定理转化为边的关系式，再结合余弦定理及基本不等式来确定角B的取值范围；利用三角关系式借助正弦定理转化为边的关系式，合理构建模型，利用椭圆的方程与几何性质来确定角B的取值范围，也是非常不错的破解方法.

(2)确定sin 2B+2cosB的最值.

方法1：(导数法1)

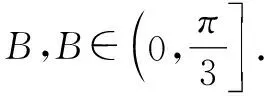
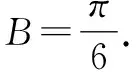
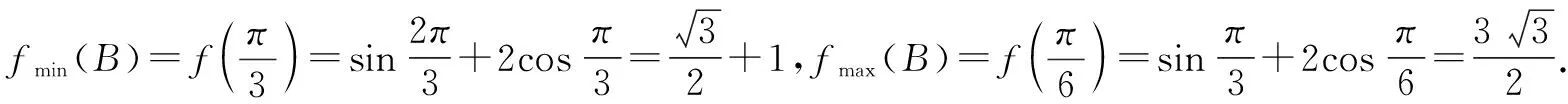
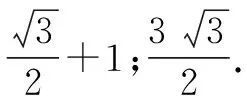
方法2：(导数法2)

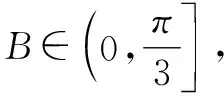
sin 2B+2cosB=2sinBcosB+2cosB

f′(x)=-(x+1)3+3(1-x)(x+1)2

=-2(2x-1)(x+1)2.

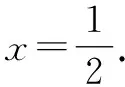
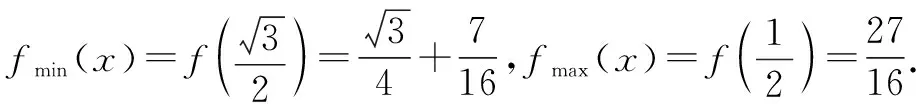
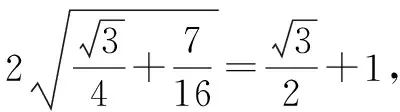
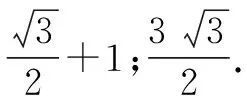
方法3：(换元法)

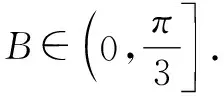
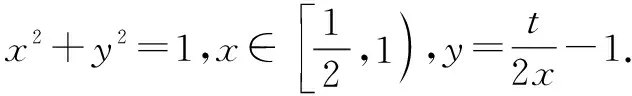
图1

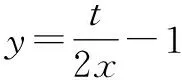
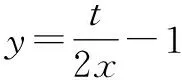
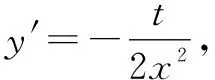
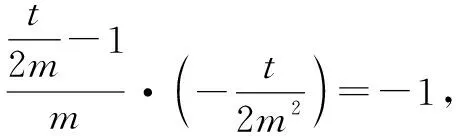
4m4=t2-2mt①

4m4+t2-4mt=0 ②

①②式联立消去mt,整理可得t=3m.

将t=3m代入4m4=t2-2mt，整理可得

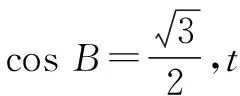
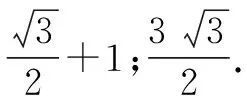
点评：在角B的限制条件下，将所求的三角关系式转化为一元函数问题，可以借助导数法来确定其最大值与最小值，这是破解此类问题中最常见的思维方式；而结合对应的三角关系式进行合理换元，把三角问题转化为函数问题，利用相应的轨迹方程以及曲线之间的关系来分析与判断最值，也是巧妙构建模型，结合数学建模来处理问题的一大创新思维.

4 链接高考

事实上，以上问题源自以下高考真题，是在高考真题的基础上加以探究、拓展与变式，融合知识，提升难度.

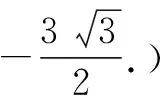
高考真题中所求解的三角函数的最值问题，没有限制条件，相比更为简单.而以上问题通过合理设置，将解三角形问题与数列问题融合，给出自变量的取值范围，并在此基础上分别求解三角关系式的最大值与最小值，难度相比高考真题来说有较大的提升，而破解方法由于考虑到最大值与最小值的差别，思维切入有所限制.

5 解后反思

对于一些典型高考真题，在学生解决问题的基础上，教师可以有针对性地加以挖掘、融合、探究、拓展，引导学生联系教材，充分把握数学知识、数学思想方法的实质，真正形成有效的数学知识体系与思维方法，从而提升知识的掌握程度，拓展数学思维能力，培养良好的数学品质，培育优秀的人文精神.