题型定位突破 过程分析总结——以二次函数与角度问题为例

江苏省苏州高新区实验初级中学 周 涛

1 引言

二次函数与角度问题属于典型问题，通常以抛物线为背景，引入几何图形构建几何角，问题解法较为特殊，具体探究如下.

2 引例探究，分步突破

2.1 引例呈现

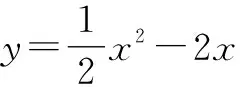
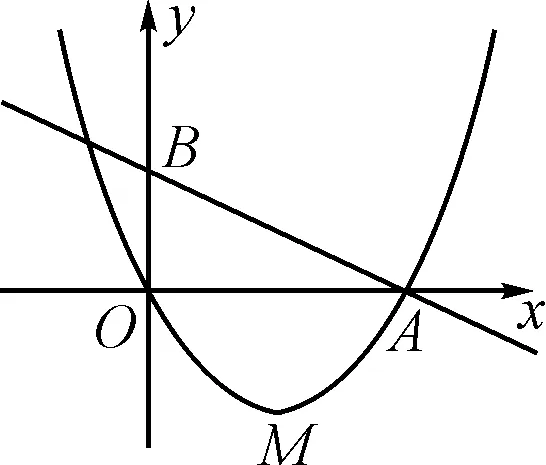
图1

(1)求b的值及点M的坐标；

(2)将直线AB向下平移，得到过点M的直线y=mx+n，且与x轴的负半轴交于点C，取点D(2，0)，连接DM，求证：∠ADM-∠ACM=45°；

(3)点E是线段AB上一个动点，点F是线段OA上一个动点，连接EF，线段EF的延长线与线段OM交于点G.当∠BEF=2∠BAO时，是否存在点E，使得3GF=4EF？若存在，请求出点E的坐标；若不存在，请说明理由.

2.2 分步突破

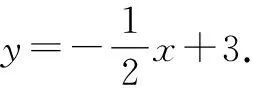
第一步——突破角度差.

第(2)问对直线AB进行了向下平移，然后设定点C，通过连线形成了几何角∠ADM、∠ACM.基于问题构建的过程，可分两阶段来证明：第一阶段，确定平移后的直线的解析式；第二阶段，确定∠ADM与∠ACM的角度关系，可进行等角转化，将角度差化为具体的角.

研究表明，当构造活动期烃源岩压力封存箱已形成时，如此时发生构造运动导致封存箱盖层破裂，则实现了压力封存箱与外界储层的沟通。这种沟通一旦实现，地下的岩层就像一个泵把流体由较深的部位抽出来，然后将其向浅处或上方压力较小的地层中排驱，迅速完成烃源岩的排烃和聚集成藏过程。构造活动期后，随着流体排出和压力降低，裂隙逐渐封闭，开始新的能量积累、压力释放和排烃过程。因此，只要有深大断裂贯穿盐膏层，在地层压力下就可形成流体运移通道，导致盐水上涌形成盐水层。

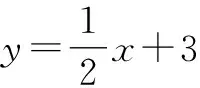
阶段二：∠ADM可视为△CDM的一个外角，则∠ADM-∠ACM=∠DMC.只需确定∠DMC的大小即可，可将其放置在三角形中.

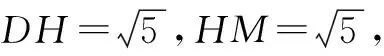
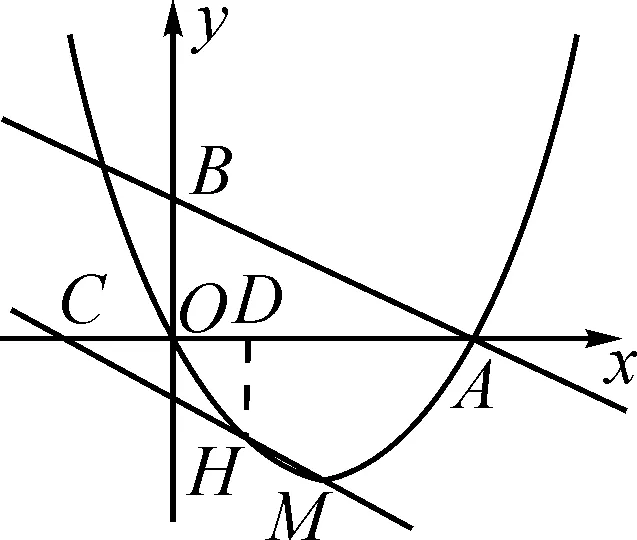
图2

第二步——突破倍角关系.

第(3)问有两个动点——点E和F，分析∠BEF=2∠BAO时，是否存在点E，使得3GF=4EF，可归结为与倍角相关的线段关系存在性问题.采用假设顺推的方式，第一阶段处理其中的倍角关系，分析几何性质；第二阶段构建线段关系，论证点E是否存在.

阶段一：假设存在点E满足3GF=4EF.分别过点G和E作x轴的垂线，垂足分别为点H和K，如图3所示.

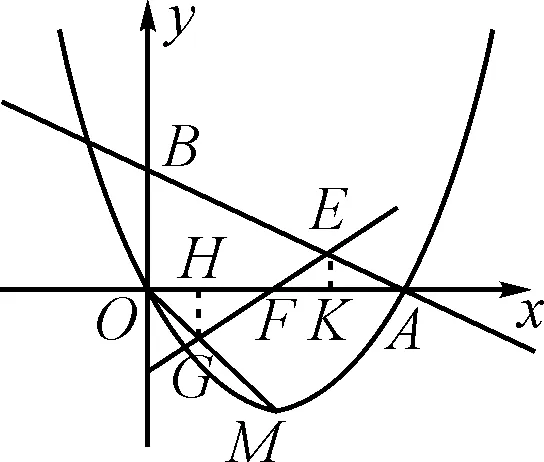
图3

因为∠BEF=2∠BAO，由∠BEF=∠BAO+∠EFA，可得∠EFA=∠BAO，即△EFA为等腰三角形，进一步可得∠EFA=∠GFH.

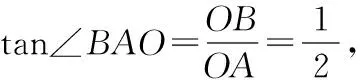
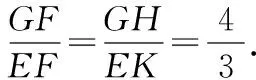
3 过程分析，方法总结

上述考题的第(2)(3)问是关于二次函数与几何角的问题，处理其中的角度问题与条件是突破的关键.下面深入分析思考过程，并总结方法.

3.1 过程评析

第(2)问属于角度和差问题.上述解析中采用等角代换的策略，将角度和差变换为具体的几何角，后续再探究该角的大小.由于问题的条件中没有设定具体角度，故由几何性质来提取特殊图形，确定特殊角.而第(3)问涉及倍角关系，充分利用了三角形的外角性质，结合倍角条件推导出了等角关系，进而提取了等腰三角形，实现了倍角条件向特殊图形的转化.

3.2 方法总结

上述第(2)问和第(3)问是关于角的数量关系问题，依托抛物线的同时，赋予了角度“数”的特性，这是该类问题的特殊所在.问题解析时，需要建立几何特性与二次函数间的关联，数形结合突破.下面总结两大问题的解析方法.

角度和差问题：角度和差涉及角度之间的加减运算，基本策略是利用几何性质转化为具体的角，去除运算符号.可利用三角形内角和定理、外角定理等进行角度换算.

倍角关系问题：倍角关系问题虽引入了角度系数，但本质上还是关于角度关系的推理.可利用几何中与倍角相关的定理，如角平分线的性质、等腰三角形性质，或构建对称关系，引入辅助圆来分析转化.

3.3 关联拓展

实际上，角的数量关系问题可分为三大类，除了上述所涉及的角度和差、倍角关系问题，还有等角问题.该类问题的突破同样需要借助特殊的几何性质，如全等特性和相似特性，可构造圆，利用圆周角性质转化角度关系.下面以一个实例进行探究.

例题已知抛物线y=ax2-2ax+c过点A(-1，0)和C(0，3)，与x轴的另一交点为B，其顶点为D.

(1)求抛物线的解析式，以及点D的坐标.

(2)如图4，点E是线段BC上方的抛物线上一点，且EF⊥BC，垂足为点F，EM垂直于x轴，垂足为点M，与BC的交点为G.当BG=CF时，求△EFG的面积.

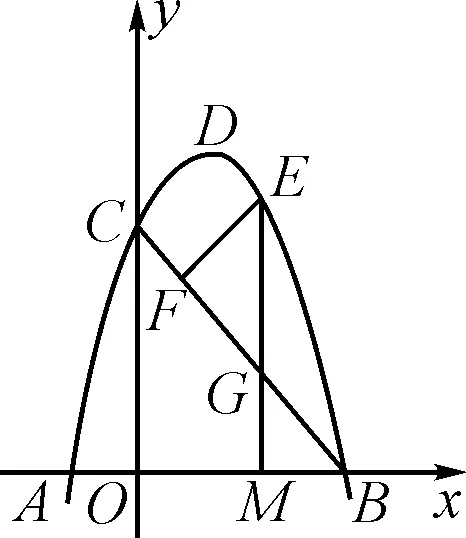
图4

(3)如图5，AC与BD的延长线相交于点H，分析在x轴上方的抛物线上是否存在一点P，使得∠OPB=∠AHB？若存在，请求出点P的坐标；若不存在，请说明理由.

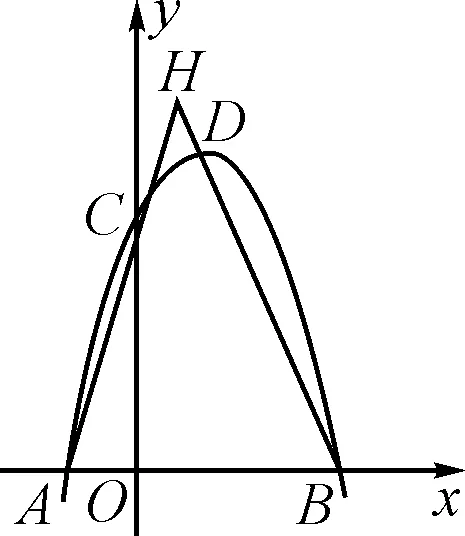
图5

解析：第(1)(2)问解答略.下面主要探究第(3)问等角关系问题.

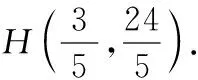
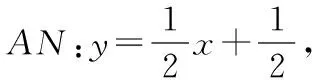
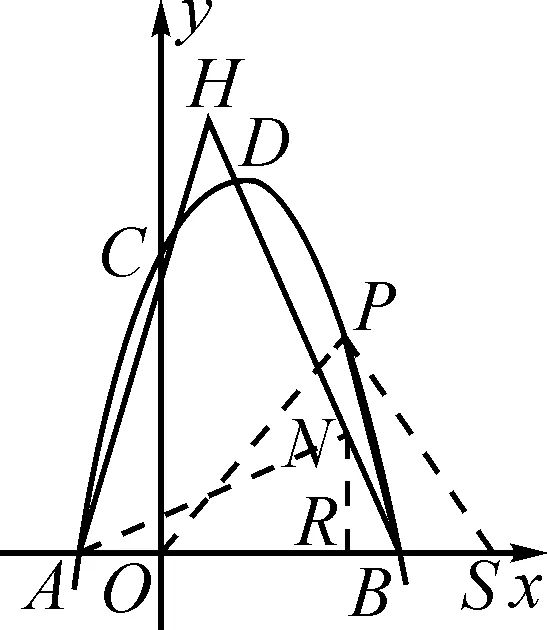
图6

过点P作x轴的垂线，设垂足为点R.在x轴上取点S，使得RS=PR，则∠RSP=45°.设P(n，-n2+2n+3)，则S(-n2+3n+3，0).

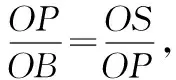
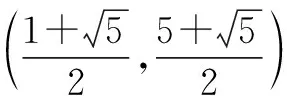
评析：上述第(3)问是关于二次函数与等角关系的问题，所涉角中其中一角为定角，可直接由几何性质确定为特殊的45°角，后续围绕点P构建特殊的等腰直角三角形，并借助三角形相似的性质确定动点P的位置.整个过程思路明确，按照“角度确认→图形构造→特性定点”的思路整合信息，构形求坐标.

4 解后反思，教学建议

4.1 归类题型，总结方法

二次函数与几何角问题属于初中数学重点和难点问题.根据角度条件，可将角度关系分为三类，包括等角问题、倍角问题和角度和差问题.上述结合实例对其加以探究，并总结了思路构建的基本策略，有助于学生后续突破类型问题.复习教学中，建议参考该种模式，引导学生定位问题类型，全面归纳题型，总结破题的基本策略.必要时，可开展对比探究，引导学生探究不同题型的特征、解法特点，从根本上掌握解题方法.

4.2 过程探究，思维培养

过程探究是解题教学的重要环节.过程探究中，可引导学生充分体验读题、审题、条件转化、模型构建、关联提取、思路形成、问题解答等重要过程，培养学生系统解题的良好习惯，促进数学思维的发展[1].以上述问题探究为例，确定问题属性，根据条件及问题进行分步解题，然后构图建模，串联条件形成思路.教学中，需关注两点：一是学生的思维活动，充分调动学生思考，可采用设问引导的方式；二是数形结合的过程，直观呈现问题，降低思维的难度，培养学生的思维习惯.

4.3 渗透思想，素养提升

解题教学还需注重数学思想培养，即教学中合理渗透数学思想方法，让学生在解题中掌握方法，感悟思想精髓，逐步提升数学素养[2].二次函数与角度类问题常涉及数形结合、化归与转化、方程思想、数学建模、分类讨论等，教学中，可立足具体的内容开展思想方法教学，感知思想方法在解题中的具体运用.如函数与图象内容渗透数形结合，二元一次方法组内容渗透方程思想，等等，将无形的思想渗透到具体的内容中，逐步提升学生的综合素养.