动中求静 巧构相似——2021年贵州省铜仁市中考数学试题第25题解析

山东省曲阜市田家炳中学 孔琳琳

1 引言

动点问题是中考数学的重要内容,解决这类问题的关键是动中求静,挖掘问题中不变的量或关系.本研究对2021年贵州省铜仁市中考数学第25题进行分析，此题以等边三角形为基本图形,考查等边三角形的性质、三角形的面积、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.

2 原题呈现

图1

(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示,不要求写x的取值范围);

(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠部分的面积S的值;

(3)当点Q落在△ABC外部时，求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示).

3 解题分析

3.1 第(1)问考查等边三角形的面积.

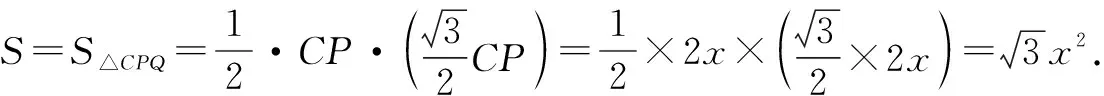
图2

本小题考查学生基本的分析和推理能力,只要分析得出当点Q在△ABC内部时,与△ABC重叠的部分就是△CPQ,即可根据等边三角形的面积公式求得.

3.2 第(2)问考查相似三角形的性质.

图3

本小题需要添加辅助线,通过相似三角形的性质,列出关系式,从而求得x的值,进而求解.

3.3 第(3)问考查割补法求图形的面积以及相似三角形的性质.

如图4中,当点Q落在△ABC外部时,设CQ交AB于点N,PQ交AB于点M,此时△ABC与△CPQ重叠部分为不规则四边形CPMN,下面提供四种利用割补法求四边形CPMN的面积的方法.

图4

解法一：(S=S△ANC-S△AMP)

如图4-1,过点N作NH⊥AC于点H,过点M作MJ⊥AC于点J,过点N作NT∥PQ交AC于点T.

图4-1

由(2)可知,CT=8,又CP=2x,

∴AT=AC-CT=4，

AP=AC-CP=12-2x.

由NT∥PQ，得△AMP∽△ANT,

∴S=S△ANC-S△AMP

解法二：(S=S△CPQ-S△MQN)

如图4-2,过点N作NT∥PQ交AC于点T.

图4-2

由NT∥PQ，得△AMP∽△ANT.

∵△CPQ为等边三角形,且CP=2x,

由(2)可知,CT=8,

∴NT=CN=CT=8，AT=AC-CT=4,

AP=AC-CP=12-2x.

由NT∥PQ，得△AMP∽△ANT,

∴MP=24-4x.

∵PQ=CQ=PC=2x,∠Q=60°,

QM=PQ-MP=6x-24,

QN=CQ-CN=2x-8，

解法三：(S=S△CHN+S梯形HJMN+S△PMJ)

如图4-3,过点N作NH⊥AC于点H,过点M作MJ⊥AC于点J,过点N作NT∥PQ交AC于点T.

图4-3

∵CT=8,CP=2x,

∴AT=AC-CT=4,AH=AC-CH=8,

AP=AC-CP=12-2x.

由NH∥MJ,得△AMJ∽△ANH.

∴AJ=24-4x,PJ=AJ-AP=12-2x.

∵CP=2x,CH=4,PJ=12-2x,

∴HJ=CP-CH-PJ=4x-16.

解法四：(S=S△MNI+S梯形CPMI)

如图4-4,过点M作MI∥CP交CQ于点I,过点N作NH⊥AC于点I、交MI于点O.

图4-4

由解法二可知,MQ=6x-24,NQ=2x-8,可得

MI=QI=MQ=6x-24,

NI=QI-NQ=4x-16.

由MI∥CP，得△NIO∽△NCH,

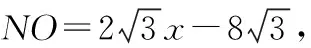
本小题所提供的解法都需要添加辅助线,通过相似三角形的性质,求得线段的长度,进而求解.解法一和解法二都是在四边形CPMN的基础上补上一个三角形得到一个规则图形,解法三和解法四都是把四边形CPMN分割为几个容易计算面积的图形.此题有一定计算难度和思维难度，要求学生要有发现问题、提出问题、分析问题、解决问题的能力.

4 反思再提高

通过以上对2021年贵州省铜仁市中考数学第25题的解析，不难发现对于三角形中的动点问题,解决问题的第一步是挖掘问题中不变的量或关系,化动为静.其次是添加辅助线构造相似三角形,通过相似三角形的性质,求得线段的长度,进而求解.

处理好动与静的关系，是解决动点问题的关键.运动是永恒的，静止则是相对的，动中有静，静中有动，相互制约，相互统一.