谈高中数学核心素养的培养——从课堂教学中数学运算的维度

⦿福建省南平市高级中学 陈 军

1 引言

我国教育事业在发展过程中，基于社会发展需要以及个体终身发展需要提出核心素养，其具有系统性与科学性特征，是我国人才培养的依据以及个体发展的目标.而在高中阶段，数学作为高中教材体系的重要科目之一，以学科特色形成的核心素养体系，重在培养学生的数学抽象、逻辑推理、直观想象、数学建模、数学分析以及数学运算能力，对学生的终身发展有着重要意义.但目前，经笔者多年工作实践发现，高中生数学运算意识与能力亟待提升.许多学生存在会而不对、对而不全、全而不优的问题，表明学生运算过程中，运算方法与程序构建上仍存在诸多欠缺.为此，本研究基于高中数学学科核心素养探究数学课堂教学过程中运算维度的培养.

2 基于学生学习需求，优化教学设计

运算维度素养的培养关键在于强化学生实践，通过应用加深理解与感悟，因此，在教学过程中选择合适的例题作为载体至关重要，但怎样界定“合适”始终为教学中的难题.具体来讲，一方面数学学科的教学是以知识为核心展开的文化教学，学生的思维活动始终在数学文化背景下进行，因此，例题要具备展现数学特征的价值，为学生思考、解决问题提供契机；另一方面，考虑到学习中学生始终为学习主体，例题的合适性应围绕学生学习的实际需求进行界定.

例1已知函数f(x)=ex，g(x)=x.求证：ef(x-2)>g(x).

题目给出后学生先自行解答，然后反馈对题目存在以下困惑：

根据题意可知ef(x-2)=eex-2，而g(x)=x，那么则出现以下两种情况：(1)当x>0时，lnef(x-2)=lneex-2=ex-2，而lng(x)=lnx；(2)当x≤0时，则出现ef(x-2)>g(x).分别对以上情况进行分析，得到以下步骤：

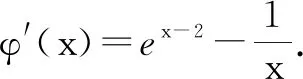
①

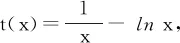
学生做到这里就无法继续求解了.

上述例题运算量较大，且考查多种运算方法，适用于考查学生综合运算能力.基于学生计算能力实际情况、发展需求，进行优化设计，重新梳理运算步骤与运算程序，可帮助学生解决困惑，掌握类型题的有效计算方法.

3 基于思维品质发展需求，优化教学策略

思维品质是个体对事物从感性认知发展到理性认知的过程，思维能力水平决定着解决问题所选择的方法，因此，数学思维的形成是学生数学运算能力乃至核心素养发展的关键.教学过程中全面了解思维品质的发展需求，吃透学生能力发展规律，配合有效的教学策略，能够显著提高教学效果与教学质量，确保学生数学思维品质的严谨性、灵活性、深刻性.

3.1 确保思维品质的严谨性

3.2 确保思维品质的灵活性

解决例1的方法有多种，但学生解题过程中遇到困难无法继续求解，表明运算方法灵活应用能力较差，需强化数学思维品质的灵活性.除上述解法外，还可采取以下方法：由于函数y=ex与y=lnx互为反函数，两函数图象对称于直线y=x，由此可知ex>x>lnx，由此判断出ef(x-2)，g(x)仅隔一条直线，直线表达式为y=x-1，通过证明ex≥x-1、x-1≥lnx也可解决问题.

3.3 确保思维品质的深刻性

通过上述问题的出现发现学生在运算过程中缺少深刻性，思维活动仅停留在数学题目给出的已知条件表象上，难以通过表面现象深刻总结知识之间联系的规律与本质，从而经常出现理解一道题而非理解一类题的情况.因此，当学生在计算某类型题目出现错误时，需要进行专项突破式训练，强化对类型题的深刻理解.

4 结束语

高中数学核心素养要求学生不仅要掌握数学知识，还要会运用数学知识、技能、思维、语言解决实际问题，形成良好思维品质.而数学是一门需要利用数字与符号进行计算、证明与推理的学科，运算思维与能力的形成均需在实践中形成，且在实践中运算能力如同解决问题的工具般影响解题效率与准确性.因此，高中生运算能力的培养需得到重视与加强，但在运算能力发展中，思维品质是基础，缺少数学思维品质将使能力发展失去核心与方向，无法构建起严谨的知识与技能体系.本文中提出了从学生学习需求、思维品质需求及个体发展出发的运算维度的培养策略，希望能给广大同仁提供一些借鉴与参考.