学科融合 数学建模
⦿甘肃省民乐县第一中学 陈国辉
1 引言
在创新新情境数学试题中,数学与其他学科的融合问题是其中最亮丽的一道风景线,巧妙把物理、化学、生物、地理、历史等其他学科中的相关知识与数学知识相结合,合理数学建模,充分体现数学教育的基础性与应用性,以及相关的数学知识、数学方法作为其他学科研究的思想与方法,备受各方关注.
2 数学与物理
例1在线段A1A2的两端点各置一个光源,已知A1,A2光源的发光强度之比为1∶2,则该线段上光照度最小的一点到A1,A2的距离之比为______.(光学定律:P点的光照度与P到光源的距离的平方成反比,与光源的发光强度成正比.)
分析:设线段A1A2的长度为l,A1,A2光源的发光强度分别为k,2k,并设出线段A1A2上光照度最小的一点P到两端点的距离分别为x,l-x,建立点P处的光照度H的函数解析式,利用导数,求H的最小值,进而确定两对应距离的比值即可.
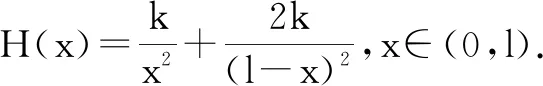
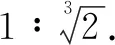
点评:合理巧妙借助物理知识与数学知识加以融合交汇,以生活实际为问题背景,通过数学建模,借助数学中的相关知识来考查数学中的最值问题.问题极具创新意识与应用意识,有效联系知识与实际.
3 数学与化学
例2如图1,C60是一种由60个碳原子构成的碳原子簇,其结构是以正五边形和正六边形组成的凸32面体,它形似足球,因此又名足球烯,则C60结构中正六边形个数为______.
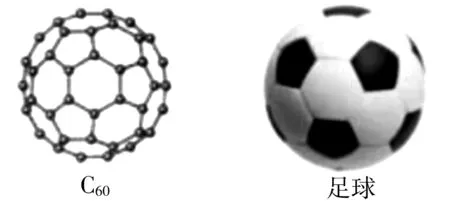
图1
分析:结合C60的结构图确定其对应的每个顶点同时在3个面内,则知正五边形的顶点个数与正六边形的顶点个数之和为60个顶点的3倍,设出两种正多边形的面的个数,建立方程组来分析与处理即可.
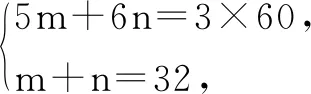
故填答案:20.
点评:合理巧妙借助化学知识与数学知识加以融合交汇.以化学中特殊的C60的结构图与生活实际中的足球加以联系,通过数学建模,结合空间几何体中顶点与面的关系,利用方程组的求解来解决立体几何中的相关数学实际应用问题.
4 数学与生物
例3面对秋冬季新冠肺炎疫情反弹风险,某地防疫防控部门决定进行全面入户排查,过程中排查到一户5口之家被确认为新冠肺炎密切接触者,按要求进一步对该5名成员逐一进行核酸检测.若任一成员出现阳性,则该家庭定义为“感染高危户”.设该家庭每个成员检测呈阳性相互独立,且概率均为p(0 分析:设出相应的事件A与B.根据相互独立来确定各自的概率,进而建立概率函数关系式f(p),通过求导,结合导函数的变形与转化,利用条件中当p=p0时,f(p)最大,进而来确定p0的值. 点评:合理巧妙借助生物知识与数学知识加以融合交汇,通过数学建模,结合概率中的相互独立建立概率关系式,综合导数及其应用来确定相应的最值问题,进而确定满足条件中的参数值. 例4台湾是中国不可分割的一部分,解放军在台海地区组织实兵演练,展现的是捍卫国家主权和领土完整的决心和能力.如图2为我空军战机在海面上空绕台巡航.已知海面上的大气压强是760mmHg,大气压强p(单位:mmHg)和高度h(单位:m)之间的关系为p=760e-hk(e是自然对数的底数,k是常数),根据实验知500m高空处的大气压强是700mmHg,则我战机在1 000m高空处的大气压强约是(结果保留整数)( ). 图2 A.645mmHgB.646mmHg C.647mmHgD.648mmHg 分析:通过阅读理解题目条件,结合关系式p=760e-hk中相关参数的分析,通过特殊的一组数值代入,得到相应的关系式,进而再次代入对应的数值,利用指数幂运算加以转化,从而确定对应的大气压强值. 点评:合理巧妙借助地理知识与数学知识加以融合交汇,通过数学建模,综合指数幂等代数运算,巧妙处理实际生活中的数学问题. 例5在《孙子算经》中有“物不知数”问题,原文如下:有物不知数,三三数之剩二,五五数之剩三,问物几何?即一个整数除以三余二,除以五余三,求这个整数.设这个整数为a,当a∈[1,500]时,则符合条件的所有a的和为______. 分析:根据题目中历史问题加以翻译转化,设整数a所表示的关系式a=3m+2=5n+3,m,n∈N*,通过新参数之间关系式的建立,结合分类讨论确定两参数之间的关系,进而合理数学建模,引入等差数列,结合等差数列的求和来确定. 解析:由题目条件,可设a=3m+2=5n+3,m,n∈N,则有3m=5n+1. 当m=5k,k∈Z时,n不存在; 当m=5k+1,k∈Z时,n不存在; 当m=5k+2,k∈Z时,n=3k+1,满足题意; 当m=5k+3,k∈Z时,n不存在; 当m=5k+4,k∈Z时,n不存在; 所以k=0,1,2,3,……,32,共有33个数,且这些数组成以8为首项,15为公差的等差数列. 点评:合理巧妙借助历史知识与数学知识加以融合交汇,通过数学建模,把历史中数学著作问题与实际数学相结合,通过条件的转化确定相应的等差数列,利用等差数列的求和来解决实际问题. 数学与其他学科相融合的创新新情境数学试题,往往紧密联系生活实际,渗透物理、化学、生物、地理、历史等其他学科中的相关知识,数学建模,巧妙转化,以考查考生的基础知识和基本能力为主线,注重数学的基础性、综合性和应用性,强调以核心素养为导向,突出考查数学建模、数据分析、逻辑推理和数学运算等核心素养,深受命题专家的青睐.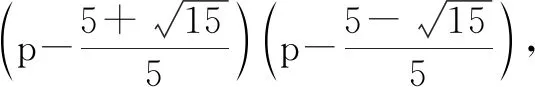
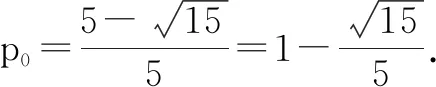
5 数学与地理

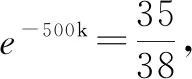
6 数学与历史
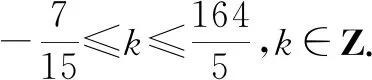
7 结束语

