化繁为简 注重学生运算能力的培养——以解析几何的运算为例

⦿江苏省兴化市楚水实验学校高中部 周小生

1 引言

运算能力是指学习者根据运算律与运算法则正确地进行运算的能力.随着新课改的推行，运算能力越来越受教育界的广泛关注.而现实生活中，因科技水平的提高与时代发展的加速，上到宇宙飞船等高科技，下到买菜做饭等日常生活，许多精准运算都被智能化机器所取代，从而导致部分学生出现运算意识薄弱的情况.鉴于此，笔者对学生当前运算状况作一些粗浅地分析，并以解析几何的运算为例，具体谈谈强化学生运算能力的得力措施，与君共勉.

2 运算能力的现状分析

2.1 教学形式陈旧，缺乏运算兴趣

现实中，仍有些教师守着陈旧的教学观念，认为运算能力的形成来自于大量的运算练习.一味地进行题海战术，希望学生能在不断的重复中熟能生巧，获得较好的运算能力.孰不知，运算能力的形成是有一定技巧的，教师应通过各种方式激发学生的探索欲，让学生能在数学思想方法的引领下，透过现象看到运算的本质，从心理上对运算产生兴趣，从而提高运算效率与能力.

2.2 运算方法机械，缺乏运算技巧

一些学生在学习上处于急功近利的状态，运算方法过于机械，主要表现在以下几方面：(1)从不考虑运算的算理、算法，认为只要运算结果正确就行；(2)看到题目，提笔就写，从不优选运算方法；(3)遇到错题也是就错论错，缺乏纠错过程，从不归纳错题出现的根源，同样的错误总是重复发生.这些状况导致学生难以体验成功的快感，长此以往形成恶性循环，导致运算信心的缺失.

2.3 教材教法脱节，缺乏运算训练

随着“减负”旗帜的竖起，教材也出现了较大的更新.小学、初中阶段的教材弱化了一些繁杂的运算，学生在心理上也对一些复杂的运算产生了避而不见的想法.但是，到高中阶段，随着教学难度的加大，对学生的运算能力提出了更高的要求，学生面临复杂、深奥的运算出现了畏难、纠结与反感的心理.因此，运算能力的培养应从小学、初中抓起，以形成良好习惯，提高学生的运算能力.

3 培养运算能力的措施

新课标提出：“数学教学应注重学生符号意识、数感、运算能力、模型思想与推理能力的培养.”解析几何在高中数学中占有举足轻重的地位，它具有知识面广、综合性强与解题方法灵活等特点.其中，对学生的运算能力也提出了更高的要求.不少学生因缺乏优化运算的能力，使得运算变得冗长繁杂，错误百出.因此，化繁为简，优化解题势在必行.

3.1 追根溯源，回归概念

概念或定义反映的是数学事物的本质属性.试题中，很多性质都由概念衍生而来.想要透过现象看到问题的本质，可从问题所涉及的概念或定义着手，将问题回归到原始的概念或定义中，问题也就迎刃而解了.

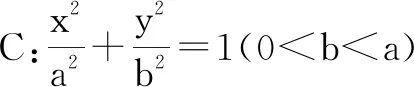
(1)求椭圆C的方程；

(2)求点T的轨迹方程.

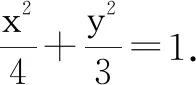
(2)设T的坐标是(x，y).当点P，T重合时，点T的坐标为(2，0)或(-2，0).

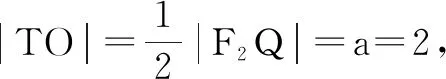
因此，点T的轨迹方程为x2+y2=4.

本题的条件中提到|F2Q|=2a，将椭圆的定义与此条件联系在一起考虑，没有任何悬念.但不少学生在解决第(2)问时，试图探寻点P与点T的坐标之间的关系，这个思路使得解题变得困难重重.因此，将问题回归到定义去考虑，使得解题变得简洁，正确率也自然提升.

3.2 只设不求，简化过程

只设不求是指为了便于解题，在解题过程中设置一些辅助参数或辅助元作为解题的跳板，学生并不需要求出这个辅助参数或辅助元，只是将它作为桥梁，之后再巧妙地消除.这种方法能简化繁杂的运算过程，同样达到解题的目的.

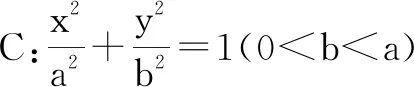
(1)求椭圆C的标准方程；

(2)假设点F是椭圆C的左焦点，点T是直线x=-3上的任意点，过点F作线段FT的垂线，并与椭圆分别相交于点P，Q.求证：OT平分线段QP(O为原点).

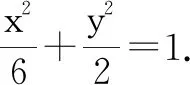
(2)根据第(1)问的结论可知F(-2，0)，设点T为(-3，m)，那么kTF=-m.

①

②

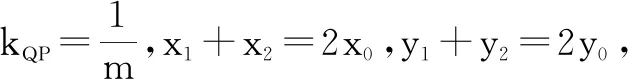
当m=0时，显然可得OT平分线段QP.

综上可知，OT平分线段QP.

第(2)问使用了点差法，巧妙地运用“只设不求”整体代换的思想，不仅减少了运算量，还有效激发了学生的数学思维，为数学运算能力的提升与核心素养的形成奠定了基础.

4 运用方程，化繁为简

人类在自然科学的研究中，为了方便表达或推导事物之间的数量关系，启用了方程法.随着时代的进步，方程运用的范围越来越广.解析几何中，有时为了避免分类讨论的烦琐，也可选择恰当的曲线方程或坐标等形式，以简化解题过程，提高解题效率.

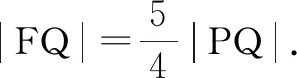
(1)求抛物线C的方程；

(2)过焦点F的直线l与抛物线C分别相交于A，B两点，如果AB的垂直平分线l′与抛物线C分别相交于点M，N，且A，B，M，N在同一个圆上，求直线l的方程.

分析：(1)抛物线的方程是y2=4x.(过程略)

(2)如果设l的直线方程为y=k(x-1)，将它与抛物线C的方程y2=4x联立求解，运算量非常大，同时还需讨论直线斜率不存在的情况，整个解题与运算过程不仅重复，还很烦琐.

如果将直线方程设成x=my+1，这个方程已经涵盖了与x轴垂直的直线，因而就少了分类讨论的环节，解题变得轻松而又准确.

由此可见，方程思想在解析几何的解题与运算中具有举足轻重的作用.因此，教学中应鼓励学生勇于探索与想象，巧妙运用方程思想突破解题困境，化繁为简，提高解题的效率.

5 结语

解析几何中对学生运算能力的考查具有较强的灵活性.因此，我们应鼓励学生从多个角度与层次去关注运算.只有运用科学、合理、灵活的运算方式，才能从真正意义上达到新课标所倡导的“减负增效”的效果.

根据具体试题，巧妙地采取相应的运算措施，不仅能提高学生的运算能力，还能促使学生形成良好的求简意识.学生在不断地训练与总结中获得运算技巧，达到以繁驭简的解题效果，从而有效地促进数学核心素养的提升.