巧借向量共线定理 妙解数学应用问题

⦿安徽省阜阳市红旗中学 常 丽

1 引言

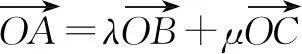
2 线性表示

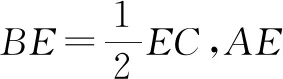
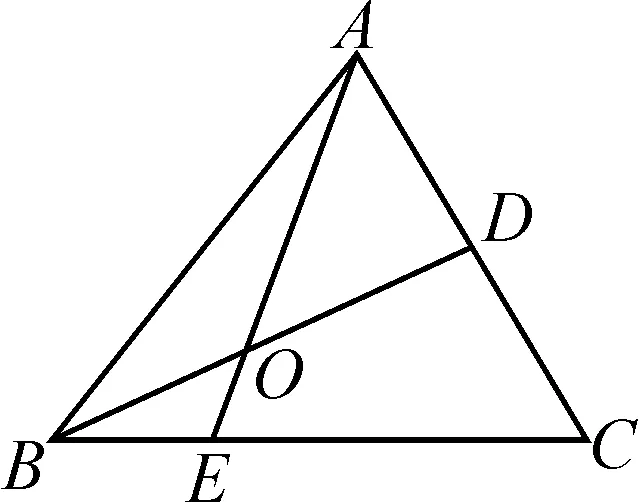
图1

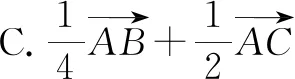
分析：根据三角形边上的点所处的位置关系，引入参数来表示相应平面向量的线性关系，结合平面向量的线性关系与运算加以转化，利用平面向量共线定理确定对应系数的关系式，进而得以确定参数值，为进一步确定平面向量的线性表示提供条件.

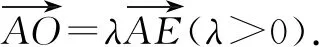
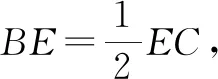
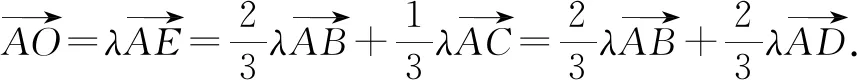
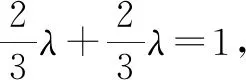
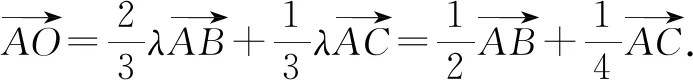
故选择答案：A.

点评：涉及平面向量的线性表示问题，关键是通过平面向量的线性关系与运算加以合理化归与转化，这其中经常会利用平面向量的中点公式、平面向量共线定理等相关知识，合理构建从条件到结论之间的关系，实现平面向量的线性表示的转化与应用.

3 参数求值

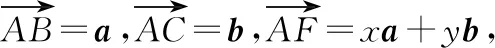
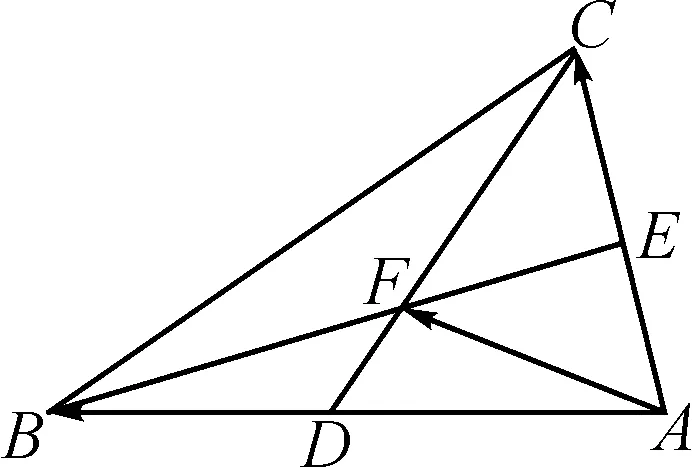
图2

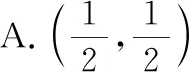
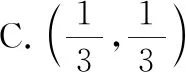
分析：利用条件中的平面向量的线性表示关系式，从不同角度与方向转化相应的线性关系式，利用平面向量共线定理分别确定对应的系数关系式，结合方程组的求解来确定对应的参数值.具体破解时，通过构建“两条线段的交点”的条件，借助转化成两次向量共线，进而确定交点位置.

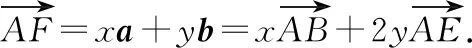
由于B，F，E三点共线，利用平面向量共线定理可得x+2y=1.

①

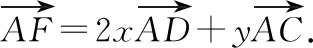
由于D，F，C三点共线，利用平面向量共线定理可得2x+y=1.

②

点评：涉及平面向量的参数求值问题，往往通过题目条件中的平面向量的线性关系式进行合理变形与转化，实现满足平面向量共线定理的条件，进而利用平面向量共线定理构建系数之间的关系式，从而得以确定对应的参数求值问题.

4 线段比例

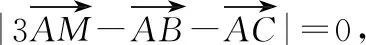
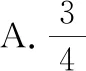
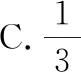
分析：根据题目条件转化为平面向量的线性关系式，引入线段的中点，利用平面向量的中点公式加以转化，构建向量之间的线性关系，利用平面向量共线定理确定对应线段的比例关系，进一步利用三角形之间面积的关系，合理确定相应的比值，从而得到对应三角形面积的比值问题.

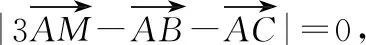
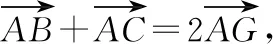
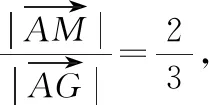
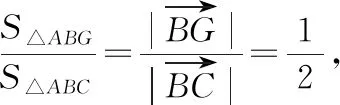
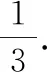
故选择答案：C.

点评：涉及平面向量的线段比例问题，破解的关键就是合理挖掘题目条件，利用平面向量共线定理，构建不同平面向量之间的线性关系，结合系数的正负取值情况确定相应线段之间的比例关系.此类问题的表示形式可以是线段比例关系的确定、三角形面积的比值、位置关系的判定等相关的应用问题.

5 求数量积

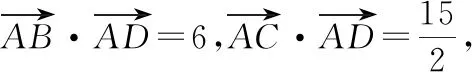
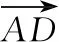
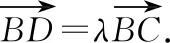
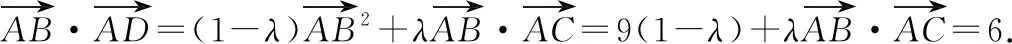
③

④

点评：涉及平面向量的求数量积问题，破解的关键是结合平面向量共线定理构建相应向量之间的线性关系，结合平面向量的数量积公式加以展开与转化，可以用来解决平面向量的数量积的求值、模的确定、系数的求解等相关问题.

6 综合应用

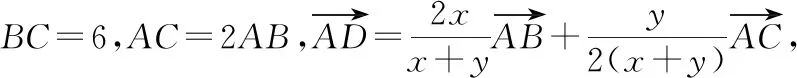
分析：通过平面几何图形中辅助线的构建，结合平面向量的线性关系式的变形与转化，结合系数之间的关系式，利用平面向量共线定理确定三点共线，从而确定对应函数的最小值的取值情况，结合余弦定理以及同角三角函数基本关系式，利用三角形面积公式的转化，结合二次函数的图象与性质来确定相应的最值问题.

解析：如图3所示，取线段AC的中点N，延长AB至点M，使得AB=BM.

图3

设AN=t>0，则AC=2t，AB=BM=t.

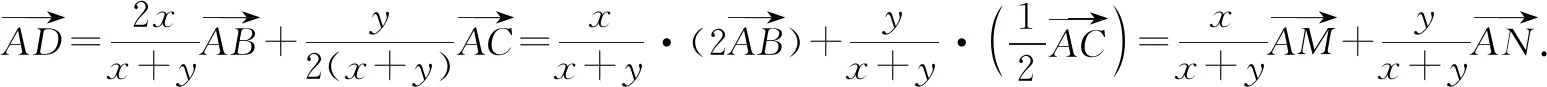
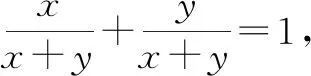
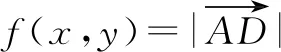
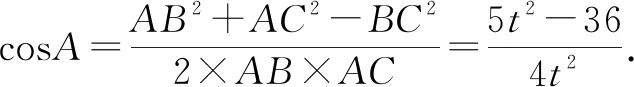
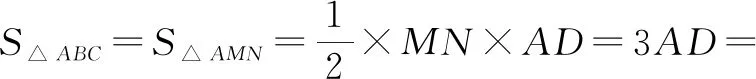
所以f(x0，y0)的最大值为4.故填答案：4.

点评：涉及平面向量的综合应用问题，往往综合平面向量、函数与方程、不等式、三角函数、平面几何与平面解析几何等相关的问题，结合题目条件，合理利用平面向量共线定理加以转化与应用，以及对应的相关知识来综合分析与应用，从而得以破解相应的综合应用问题.

7 结束语

作为平面向量中最基本的定理之一的平面向量共线定理，可以合理有效地构建起不同向量之间的线性关系以及不同点之间的位置关系.具体应用时主要涉及几个方面：一是正用，即利用定理证明向量共线(或三点共线、线线平行)等；二是逆用，即已知两个向量共线，那么其中一个向量必然可用另一个向量线性表示；三是综合应用，即利用向量的工具性来解决一些综合性应用问题.