导数应用复习中的四个基本点

⦿安徽省郎溪中学 程远林

1 引言

导数是解决函数性质问题的重要工具，导数应用问题类型多样、方法灵活，对学生基础知识的掌握程度及灵活应用能力要求较高.基于此，笔者对导数应用的复习提出四点基本要求，希望对学生复习有所帮助.

2 巩固基础知识

导数应用模块中所涉及的基础知识主要包括导数的定义、导数的几何意义、基本初等函数的求导公式、导数的运算法则，利用导数求函数的单调区间、极值、最值等.

以求函数的单调区间为例，基本步骤是：先求函数的定义域，再求导，令导数为0，解得导函数的零点，最后判断每个零点左右两侧导数的符号，从而确定函数的单调区间.

例1已知函数f(x)=2x3-ax2+b，讨论f(x)的单调性.

解析：f′(x)=6x2-2ax=2x(3x-a).

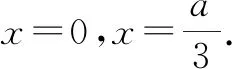
当a=0时，f′(x)≥0,f(x)在(-∞,+∞)上单调递增；

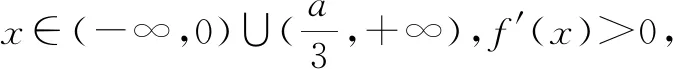
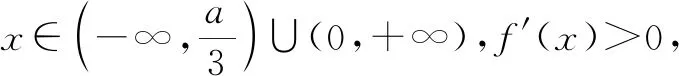
点评：此类问题求解中常涉及分类讨论，要注意分类标准的确定.以导函数是二次函数为例，要讨论的主要有：二次函数的开口方向(讨论二次项系数)，二次函数有无零点(利用判别式进行讨论)，所求的零点是否在定义域范围内，零点的大小是否确定等.

3 归纳基本题型

应用导数可解决的问题类型，如函数不等式的证明问题，不等式恒成立、能成立、恰成立问题，函数的零点问题等.题型虽然各异，但基本方法都是构造函数求函数的最值.

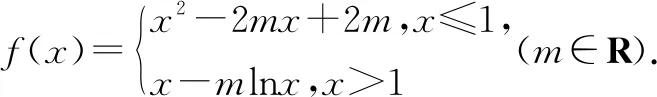
(1)∀x∈(-∞,+∞),f(x)≥0恒成立，求m的范围；

(2)∃x0∈(-∞,+∞),f(x0)≤0，求m的范围；

(3)f(x)∈[0,+∞)，求m的值.

解析：(1)属于不等式恒成立问题，任意函数值均大于或等于0，故只要fmin(x)≥0即可，因此转化为求函数的最小值.

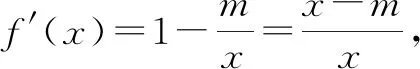
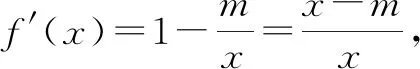
综上得满足条件的m的取值范围是[0,e].

(2)属于不等式能成立问题，即存在某一个函数值小于或等于0，故只要fmin(x)≤0即可.

当m≤1，且x>1时，f(x)=x-mlnx，同(1)知fmin(x)>f(1)=1.x≤1时,f(x)=x2-2mx+2m,fmin(x)=f(m)=2m-m2.由2m-m2≤0，得m≤0或m≥2.所以m≤0.

当m>1，且x≤1时,f(x)=x2-2mx+2m,fmin(x)=f(1)=1.x>1时，f(x)=x-mlnx，同(1)知fmin(x)=f(m)=m-mlnm=m(1-lnm)，由1-lnm≤0，得m≥e.

综上得满足条件的m的取值为范围是(-∞,0]∪[e,+∞).

(3)属于恰成立，即函数的最小值等于0.

当m≤1，且x>1时，f(x)=x-mlnx，同(1)知fmin(x)>f(1)=1.x≤1时,f(x)=x2-2mx+2m,fmin(x)=f(m)=2m-m2.由2m-m2=0，得m=0或m=2.所以m=0.

当m>1，且x≤1时,f(x)=x2-2mx+2m,fmin(x)=f(1)=1.x>1时，f(x)=x-mlnx，同(1)知fmin(x)=f(m)=m-mlnm=m(1-lnm)，由1-lnm=0，得m=e.

综上得满足条件的m的值为：m=0，或m=e.

点评：对于给定条件下f(x)≥g(x)恒成立问题，可通过作差或作商合并构造函数求最值.对于给定条件下f(x1)≥g(x2)恒成立问题，要分别求两个函数的最值.

4 提炼基本方法

师傅领进门，修行在个人.在同一模块中学生所学的基础知识是一样的，但应用中往往有多种不同的方式，对于同一题目的解答，有的学生方法简洁、有的学生思路繁琐，因此要择优而用.

例3(2020年高考全国卷Ⅰ)已知函数f(x)=ex-a(x+2).

(1)当a=1时，讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.

解析：(1)当a=1时，f(x)=ex-x-2，求导得f′(x)=ex-1，由f′(x)=0得x=0，所以在区间(-∞,0)上,f′(x)<0,f(x)单调递减；在区间(0,+∞)上,f′(x)>0,f(x)单调递增.

(2)解法1：f′(x)=ex-a.

当a≤0时，f′(x)>0,f(x)在定义域内递增，则f(x)至多存在一个零点.

当a>0时，由f′(x)=ex-a=0,得x=lna，则在区间(-∞,lna)上,f′(x)<0,f(x)单调递减；在区间(lna,+∞)上,f′(x)>0,f(x)单调递增.fmin(x)=f(lna)=-a(1+lna).

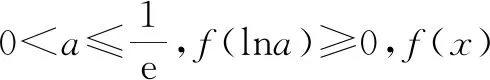
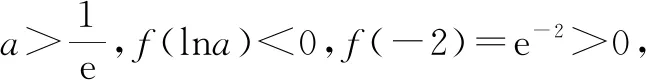
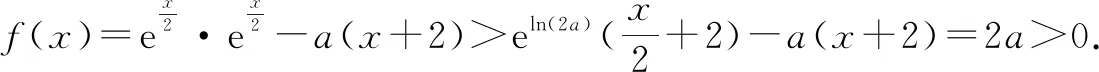
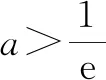
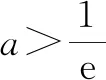
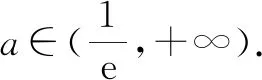
解法2：易知x=-2不是函数的零点.

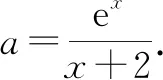
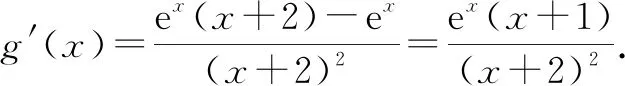
解法3：由ex-a(x+2)=0,ex=a(x+2)，则问题转化为函数y=ex与y=a(x+2)有两个交点.而y=a(x+2)过定点(-2,0)，当a≤0时，只有一个交点；当a>0时，可通过寻找临界状态来确定，即求y=ex过(-2,0)的切线斜率即可.

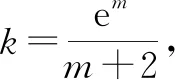
点评：上述三种方法各有优劣.方法1是处理此类问题的标准方法，命题组提供的答案也是这种方法，难点是零点所在区间判定时，特殊值的选取，借助放缩构造法，这种方法对学生基本技能要求较高.方法2通过分离参数，方法3利用了分离函数，将所求的零点问题转化为两个函数图象的交点问题来处理.三种方法所用的知识原理都是学生所熟悉的，但如何应用这些知识解决相同的问题，对学生提出了更高的要求.

5 提升基本技能

例4已知函数f(x)=xlnx.

(1)略；

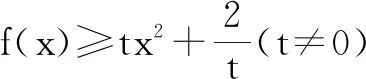
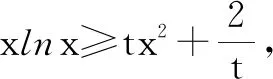
所以，t的取值范围是[-e3,0).

点评：对数学思想的考查，是高考命题的重要理念之一.从导数的应用来看，涉及多种数学解题思想.如“分类讨论思想”“化归转化思想”“数形结合思想”“一般与特殊思想”有限与无限思想”等等，而本题的求解体现了化归转化思想.这些方法的应用对学生分析、解决问题的能力提出更高要求.