具有时滞的湖泊生态模型的动力学性质分析

丁宇婷，周 林

(东北林业大学 理学院，哈尔滨150040)

我国湖泊生态系统具有湖泊数量多、分布范围广、水质优良、可持续能力强等优点[1].在人与自然这一复杂而庞大的系统中，湖水是沟通自然界各系统、各圈层的纽带.湖中有大量的初级和二级生产群体，还有最复杂的微生物群落，它们之间是相互影响、相互作用的，其中浮游生物是主体，主要由浮游植物和浮游动物组成[2-3].

随着社会经济发展，对自然资源的利用程度和保护力度不匹配，湖泊流域内的资源、生态环境受到了外界的巨大威胁.不加处理、过度排放的工业废水、生活污水，使得附近流域中有机物、无机物的含量增加，引起水体中的浮游植物爆炸性生长，意味着水体富营养化.湖泊中有些浮游植物是有毒的，释放的毒素可以通过食物链到达其他生物体内，进而导致湖泊生态系统失衡.有害生物对自然生物、公共卫生等都有很大的影响[4].有时，藻类的过度繁殖也可导致某些流行传染病.有相关的研究表明，孟加拉湾的水华事件可能是引起孟加拉国爆发霍乱的主要原因[5].目前我国的部分湖泊流域生态稳定性受到严重威胁，湖泊所在地区的生物多样性被严重破坏[6].文献[7]通过对我国的部分流域中的浮游植物和生境因子进行取样发现，环境对浮游植物的生长具有重要影响.水生植物和硅藻群落的生长情况会随着所在区域的水文条件的改变而变化[8].风浪、风暴不仅会影响湖泊水质的清澈程度，也会导致湖泊水生植物发生机械性损伤[9].浮游生物对外界环境的变化非常敏感，其状态在一定程度上可以反映出所在区域的水体环境和水体富营养化情况[10-11].浮游植物作为湖泊中的重要生产者，其生长状态和群落结构的改变可以作为预示湖泊环境变化的重要指标[12].1987年Brown指出湖水中的生物及其生境因子共同组成湖泊生态系统，湖泊的物理性质、物质循环、生态系统的结构与功能会随着气候的变化而变化[13].

本文通过计算模型的正平衡点，计算在正平衡点处的特征方程，分别讨论分析在无时滞时正平衡点的全局渐近稳定性、具时滞时正平衡点的局部渐近稳定性与Hopf分支的存在性，最后通过数值模拟来验证理论分析的结论，并给出生物学解释.

1 模型正平衡点的存在性和稳定性

1.1 正平衡点的存在性

从传统意义考虑湖泊生态系统的内部因素-浮游植物与浮游动物之间的捕食关系，可以用Lokta-Volterra模型来描述[14]：

然而湖泊生态系统不是封闭的，其稳定性不仅只与浮游植物、浮游动物有关，也与外来有机物的输入有关，文献[14]提出了外来有机物-浮游植物-浮游动物模型：

(1)

在实际中，延迟现象在生态系统是很常见的.外来有机物对湖泊生态系统产生作用需要一定的时间，系统对于外来物质影响的反馈响应不具有瞬时性.浮游动物对外来有机物作用的消费反应有延迟性.在这里，我们假设浮游动物将食物转化为自身增长的时间是τ，接下来讨论文献[15]中提出的具有时滞的外来有机物-浮游植物-浮游动物模型：

(2)

其中：C(t)表示外来有机物的含量，P(t)表示浮游植物在t时刻的种群密度，Z(t)表示浮游动物在t时刻的种群密度，a表示浮游植物的内禀增长率，b表示浮游动物对浮游植物的摄取率，c表示浮游动物食用浮游植物的转化率，γ表示浮游植物的增长率，k表示外来有机物单位时间内的流入量，δ表示湖中的外来有机物沉入湖底的比率，β0表示浮游动物对外来有机物的摄取率，β1表示浮游动物的捕食能力，β2表示浮游植物转化为浮游动物增长的比率，β3表示外来有机物转化为浮游动物增长的比率，d为浮游动物的死亡率.

模型(2)不考虑时滞时即模型(1)，模型(2)与模型(1)的平衡点是一致的.通过计算，模型的正平衡点如下：

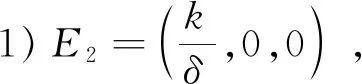
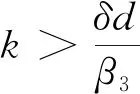
接下来，我们只讨论正平衡点E3，其余的平衡点可以类似的进行讨论.

1.2 无时滞时正平衡点的全局渐近稳定性

通过构造合适的Lyapunov函数，结合LaSalle不变性原理，证明该平衡点的全局渐近稳定性，叙述为如下的引理.

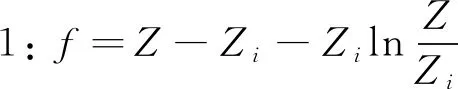
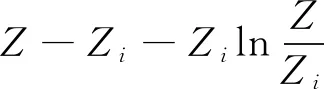
f(z)=z-1-lnz

对f(z)求导得到：

当z>1时，f′(z)>0，即f(z)在z>1时是单调递增的，在z=1处取得最小值0.当1>z>0时，f′(z)<0，即f(z)在1>z>0时是单调递减的，在z=1处取得最小值0.

证明：构造如下的Lyapunov函数：

对于任意的t>0，V(t)是非负的.V(t)对t求导得到：

δC+β0C3Z3+δC3)+d(Z3-Z)+

C3Z-CZ)+(d-β3C)(Z3-Z)+β2P3(Z-

1.3 具时滞时正平衡点的局部渐近稳定性与Hopf分支分析

我们先计算正平衡点E3处的特征方程，正平衡点E3对应的Jacobian矩阵是：

则系统(2)在正平衡点E3处的特征方程是：

λ3+a2λ2+a1λ+a0+(b2λ2+b1λ+b0)e-λτ=0

(3)

其中：

a2=δ-γ+d+β1z3+β0z3

a1=-δγ-γd+δd-β0γz3+β1dz3+β0dz3+

b2=-β3c3-β2p3

b1=-δβ3c3+γβ3c3-δβ2p3+γβ2p3-

β0β2z3p3-β1β3z3c3

b0=-δβ1β3z3c3+γβ0β2z3p3+γδβ2p3+γδβ2c3

接下来，在τ>0时，讨论是否满足横截条件.

将λ=iw代入特征方程(3)中得到：

-iw3-a2w3+a1iw+a0+(-b2w2+ib1w+b0)(cos(ωτ)-isin(wτ))=0

分离实虚部得到：

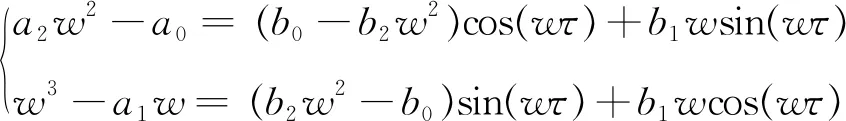
(4)

从中解出sin(wτ)，cos(wτ)：

cos(wτ)=

sin(wτ)=

对(4)中的两个式子，等号两边平方相加，令η=w2得到：

g(η)=η3+pη2+qη+r=0

(5)

其中：

我们作如下假设：

得到如下结论：

引理3：(i)当(H1)成立时，方程(5)有正实根；(ii)当(H2)成立时，方程(5)没有正实根.

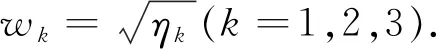
(6)

k=1,2,3;j=0,1,2,…

其中：

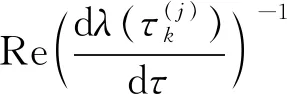
[3λ2+2a2λ+a1+(2b2λ+b1)e-λτ-τ(b2λ2+b1λ+b0)e-λτ]dλ=[λ(b2λ2+b1λ+b0)e-λτ]dτ

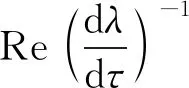
将cos(wτ)，sin(wτ)代入化简得：

(7)

综合以上分析，有如下结论：

定理：

1)如果(H1)成立，则当τ>0时，正平衡点E3是局部渐近稳定的；

2)如果(H2)成立，则当τ∈(0,τ0)时，正平衡点E3是局部渐近稳定的，并且随着τ的增加，该平衡点的稳定性会交替变化.

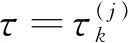
2 数值模拟

2.1 无时滞时正平衡点的全局渐近稳定性

对正平衡点E3=(3.046 9,0.329 7,3)的全局渐近稳定性进行数值模拟，验证结论.文献[17]得出以下结论：结合实际意义，浮游动物摄取吸收物质的量小于自身增长的量，即β0>β3，β1>β2，我们取文献[14]中的参数值：

γ=0.48，d=0.2，δ=0.2，β0=0.15，β1=0.16，β2=0.14，β3=0.05.

根据引理2的条件，取参数k=1，三个不同的初值：(3.0,0.3,2.9)，(12.9,6.8,11.7)，(27.2,11.9,28.8)，如图1所示.

图1 正平衡点E3是全局渐近稳定的

由图1知，无论是在正平衡点附近，还是选取离正平衡点较远的初值，随着时间的增长，图中的曲线逐渐趋于同一条曲线，即在无时滞的情况下正平衡点是全局渐近稳定的，与理论分析一致.

2.2 具时滞时正平衡点的局部渐近稳定性

文献[14]有这样的结论：k的取值应该小于平衡点稳定时k的临界值.我们取文献[14]中的参考数值：

γ=0.48，d=0.2，δ=0.2，β0=0.15，β1=0.16，β2=0.14，β3=0.05，k=2.

通过计算得到：

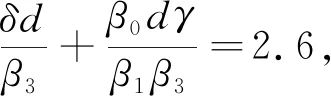
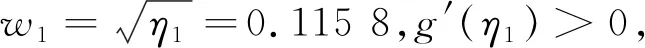
所以τ0=5.299 3，结合上述分析，得到：

1)当τ∈(0,τ0)时，正平衡点E3是局部渐近稳定的.图2给出了τ=0.3,τ∈(0,τ0)时的数值模拟.

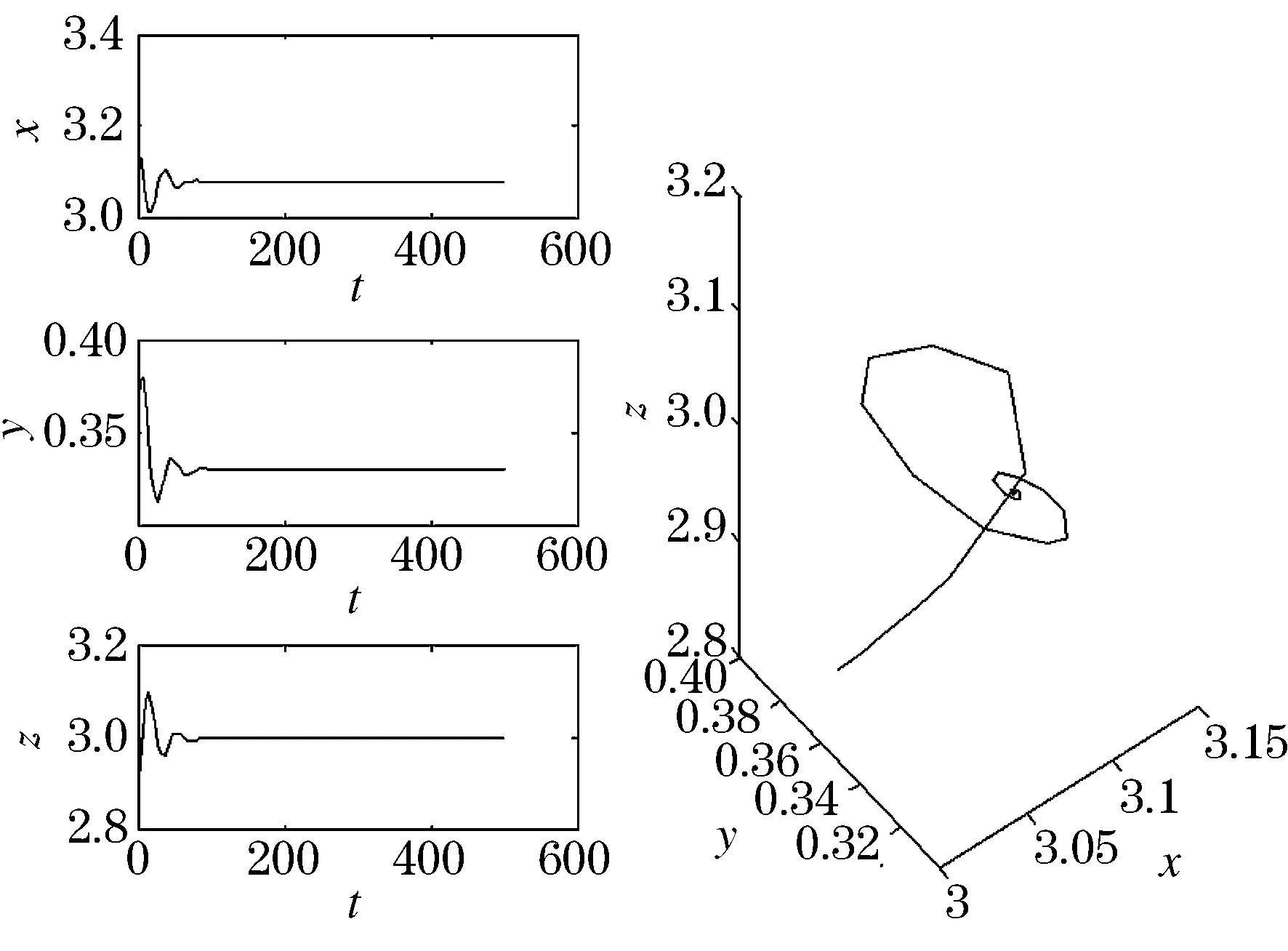
图2 τ=0.3时，正平衡点E3是局部渐近稳定的

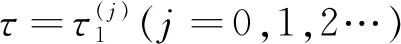
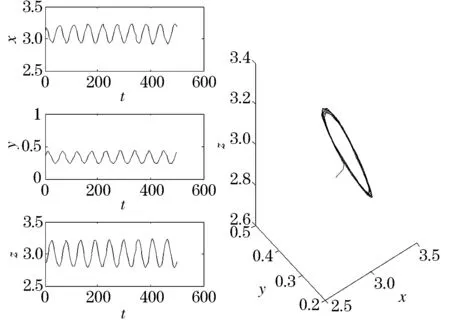
图3 τ=5.3时，正平衡点E3处产生Hopf分支周期解

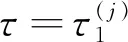
对于正平衡点E3，由图1知，在无时滞时是全局渐近稳定的；由图2、3知，当时滞在某些范围内时，是局部渐近稳定的，并且在时滞临界值附近产生Hopf分支，即浮游植物和浮游动物以密度周期性改变的方式共存.这说明当τ=0时，该正平衡点稳定，浮游植物和浮游动物以稳定的状态共存，即如果外来有机物含量比较少，对湖泊生态系统的稳定性影响不大.当τ>0时，该正平衡点的稳定性改变.说明时滞对湖泊生态系统的稳定性有很大影响，外来有机物的输入也是影响湖泊生态稳定性的重要因素.由于湖泊附近环境不同，所含外来有机物的量是不同的，因此，选择不同的k值是符合实际的.

3 结 语

本文先计算模型的正平衡点，在模型无时滞时，构造合适的Lyapunov函数，结合LaSalle不变性原理，证明该正平衡点是全局渐近稳定的.在模型具时滞时，计算在正平衡点处的特征方程，分析得到，当时滞τ∈(0,τ0),τ0=5.299 3时正平衡点E3是局部渐近稳定的，在临界的时滞附近产生Hopf分支.对时滞为零、时滞不为零两种情况，分别给出数值模拟.通过对比说明，时滞是影响湖泊生态系统的重要因素，这是符合实际的.