基于点云边界质心的粗配准方法

陆尚鸿，李文国

(昆明理工大学 机电工程学院,云南 昆明 650500)

近年来，随着计算机软硬件设备不断发展和三维扫描设备日趋完善，人们能够较为轻松地获取高精度的点云测量数据[1]。因此，基于点云的三维重建技术被逐渐应用在地形测绘[2]、无人驾驶[3]、机器人技术[4]、虚拟现实[5]、逆向工程[6]、文物保护[7]等领域。由于测量环境、设备安装角度和被测物体尺寸大小的限制，采集到的点云数据往往会出现部分特征和信息缺失的情况，所以需要从多个角度对物体表面进行多次数据采集。然后，将不同视角的点云数据合并到同一坐标系下，并通过坐标转换使那些反映物体同一外貌特征的点集相互重合，形成一个完整的点云数据，这个过程就是点云配准[8]。点云的粗配准大体可分为基于全局搜索、概率统计和局部特征3类。

四点法(4-Points Congruent Sets，4PCS)[9]及其改进算法都属于基于全局搜索的粗配准。这类算法会从源点云选择一些共面的四点，根据仿射不变性原理从目标点云中寻找符合条件的四点集合，并求出之间的变换矩阵。超级四点法(Super Generalized 4-Points Congruent Sets，SG4PCS)[10]中加入了角度特征量，通过比对四点之间的夹角来加快原始点云和目标点云中对应四点的匹配。基于关键点的四点法(Keypoint-based 4-Points Congruent Sets，K-4PCS)[11]采用关键点提取技术取代4PCS随机共面四点采样法，提高了算法计算速度。语义关键点四点法(Semantic Keypoint-based 4-Points Congruent Sets，SK-4PCS)[12]中加入了分层处理和特征点分类功能，在截面中提取到特征点后，根据交点、顶点等几何特征对点进行分类，然后根据特征点类型优化配准策略。这类算法粗配准精度较高，但配准速度普遍较慢，而且由于算法对源点云中共面四点的采样具有随机性，容易寻找出错误的对应点[13]，从而出现配准精度降低的问题。

1 算法描述

本文提出一种基于边界质心的点云粗配准方法。该算法首先对源点云和目标点云分别进行边界提取[14]。点云边界作为表达物体表面几何特征的重要载体，对曲面重构精度起着重要作用。提取后的点云边界能在最大程度保持物体原有表面特征的同时，减少点云内部无特征的数据点。然后，计算点云边界质心，并把两个点云的边界质心都移动到坐标原点，使待配准点云初始距离快速减小，增加源点云和目标点云之间的重叠度，减少出现错误配准的几率。最后，使用K-4PCS算法完成粗配准。本文方法的流程图如图1所示。

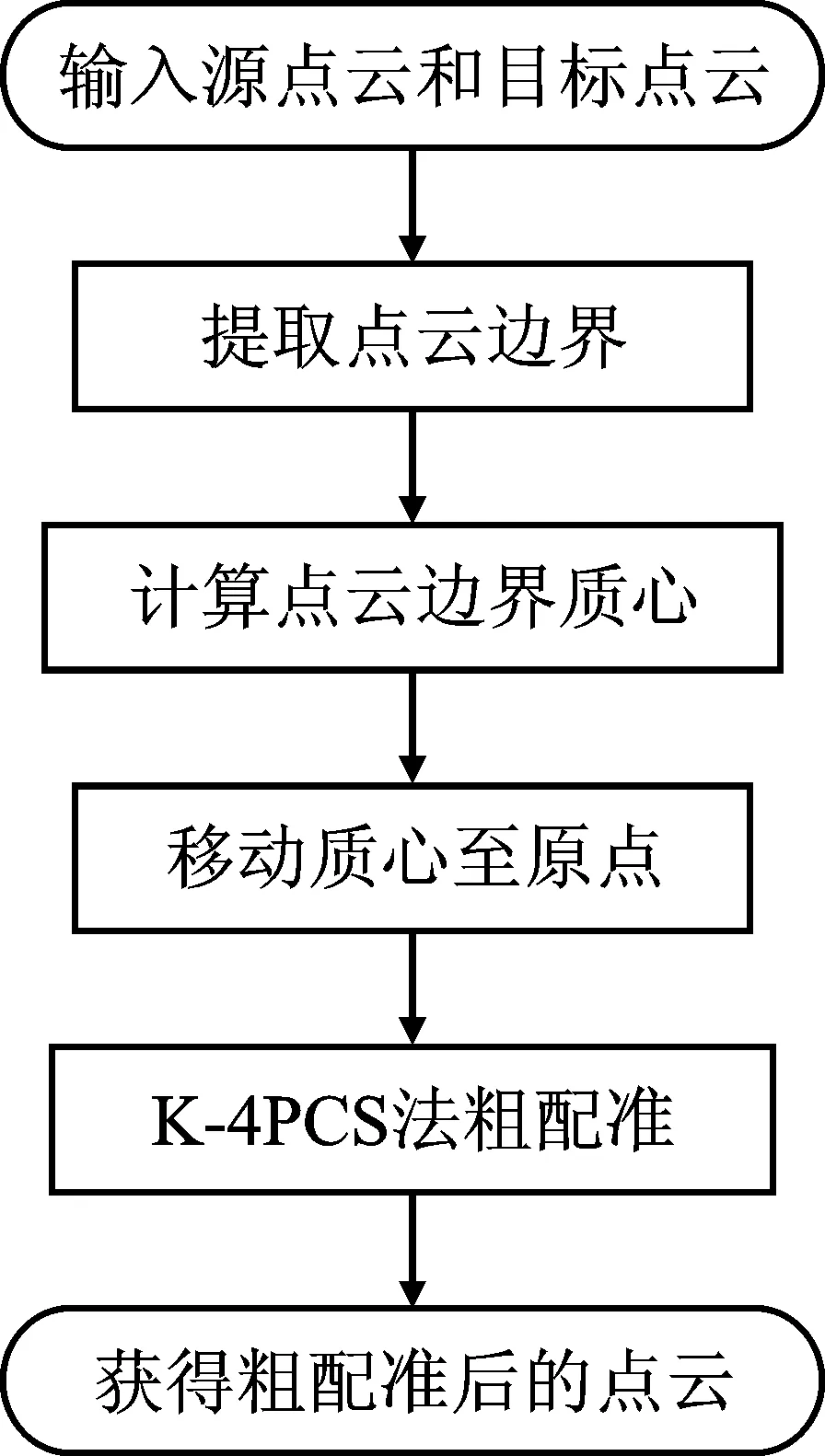
图1 点云粗配准流程图Figure 1. Flow chart of point cloud coarse registration

2 点云边界提取算法

2.1 拓扑关系的建立与邻近检索方法

K-D tree是一种树形数据结构，常用于点的快速检索[15]。创建K-D tree时，通常随着树的深度增加，轮流选择x、y、z轴，过轴方向上坐标为中位数的点，作垂直于该轴的分割面。通过这种方式不断划分点云所在的三维空间，直到所有数据点都划分完毕。建立K-D tree能加快点的最邻近检索[16]。为了搜索点P的最邻近点，需要先沿着K-D tree搜索到点P，此时的点P作为当前节点。如果点P到其父节点的距离小于点P到当前节点的祖父节点所在分割面的距离，则点P的父节点即为点P的最邻近点。此时，点P及其最邻近点被分割在同侧子空间中，如图2所示。

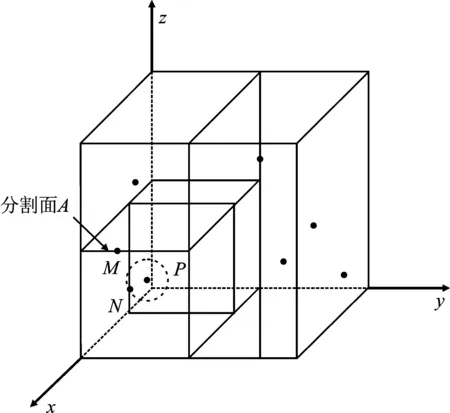
图2 最邻近点在同侧子空间Figure 2. The nearest point is in the same side subspace

由图2可以看出，点P为当前节点，点N为点P的父节点，点M为点P的祖父节点，分割面A为过点M且垂直于z轴的分割面。以点P为球心，以PN为半径作球，当球与分割面A相离时，父节点N即为点P的最邻近点。

当点P到其父节点的距离大于点P到当前节点的祖父节点所在分割面的距离时，则需考虑最邻近点在另侧子空间的情况。此时，先记录下点P到其父节点的距离，然后沿K-D tree搜索路径逆向查找，当前节点位置向树的上方移动一级。在另侧子空间中找出距离点P最近的点，比较两个距离的大小，算出当前最小距离。然后比较当前最小距离和点P到当前节点的祖父节点所在分割面的距离。如果前者小于后者，则当前最小距离即为真实最小距离，所对应点为最邻近点；如果不是，则以相同的方法继续向上回溯，直到找出满足要求的最邻近点，具体如图3所示。

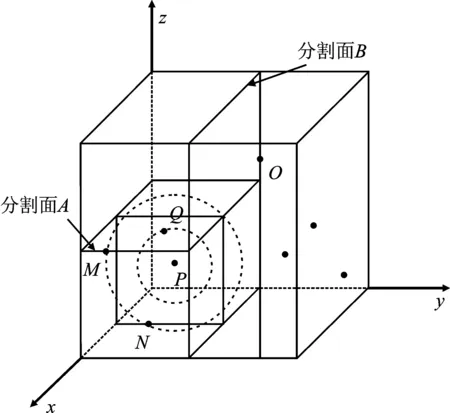
图3 最邻近点在另侧子空间Figure 3. The nearest point is in the other subspace

由图3可以看出，以点P为球心，以PN为半径作球，球与分割面A相交，记录下PN的距离。沿着K-D tree逆向查找，当前节点位置向上移动一级，变为点P的父节点N，分割面B为过点N祖父节点O且垂直于y轴的分割面，点Q为另侧子空间的最近点，比较PQ和PN的大小，PQ较小。以点P为球心，PQ为半径作球，球与分割面B相离，则点Q为点P的最邻近点，最邻近检索算法如图4所示。

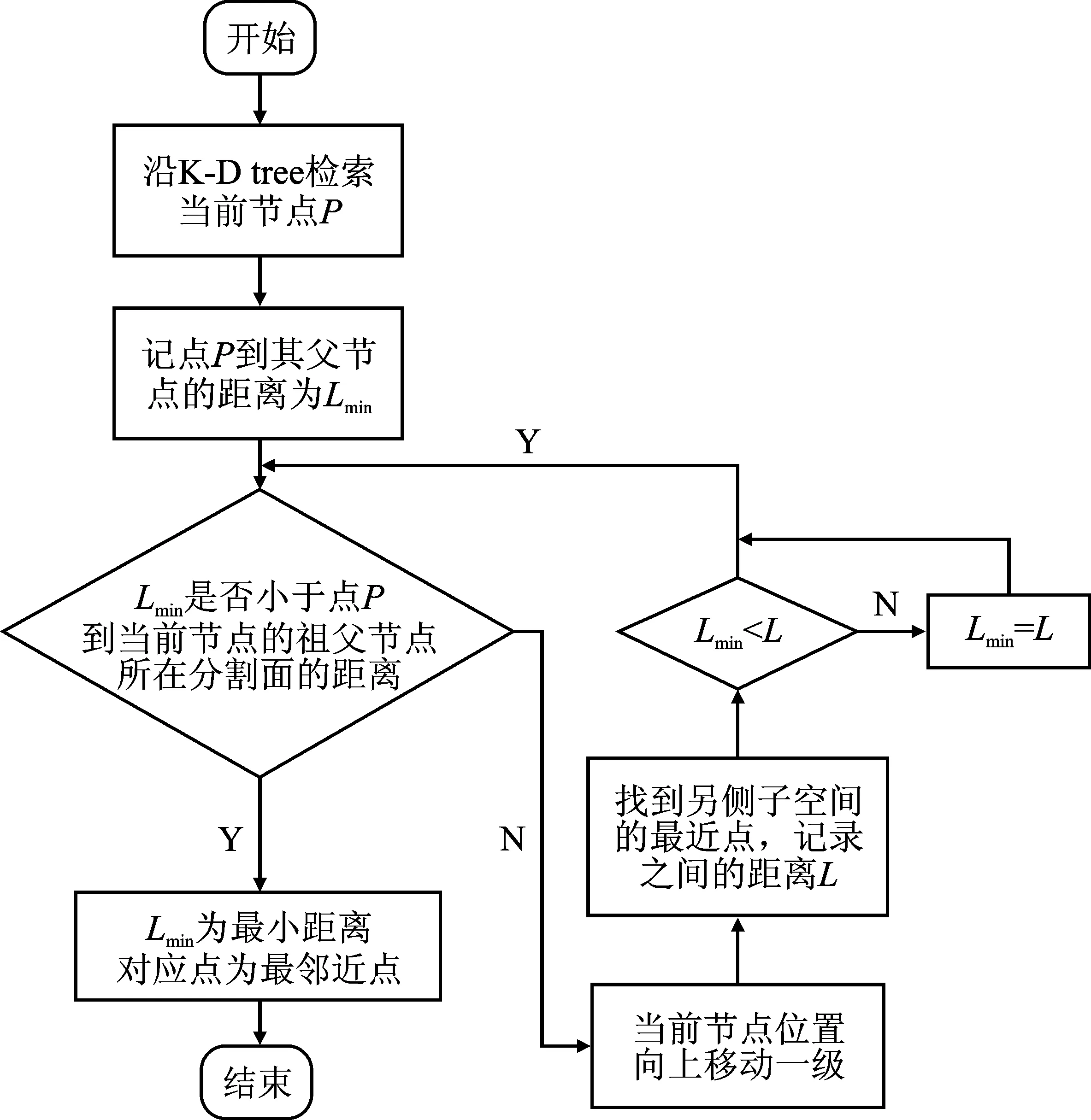
图4 最近邻点算法流程图Figure 4. Flow chart of the nearest neighbor algorithm

2.2 平面的拟合

运用K-D tree的k邻近算法，可以快速查找点P的k个邻近点，距离从近到远依次记为N1,N2…,Nk。设拟合平面的方程为

ax+by+cz+d=0

(1)

把点P及其k个邻近点的坐标带入式(1)中，其矩阵方程为AX=0。

(2)

用最小二乘法来拟合平面，当某平面到点P及其k个邻近点的距离平方和最小，该平面即为其拟合平面，点到平面的距离平方和可以表示为

(3)

求平面到点P及其k个邻近点的距离平方和最小，等同于求X使式(3)的值最小。用奇异值分解法(Singular Value Decomposition，SVD)求解，当式(3)取最小值时，其值为ATA的最小特征值，X的值为最小特征值所对应的特征向量[17]。

2.3 边界点的判断与提取

把点P及其k个邻近点投影到拟合平面上，得点P′,N′1,N′2，…,N′k。以P′为起点，以k个邻近点的投影为终点，作向量P′N′1,P′N′2，…,P′N′k，如图5和图6所示。

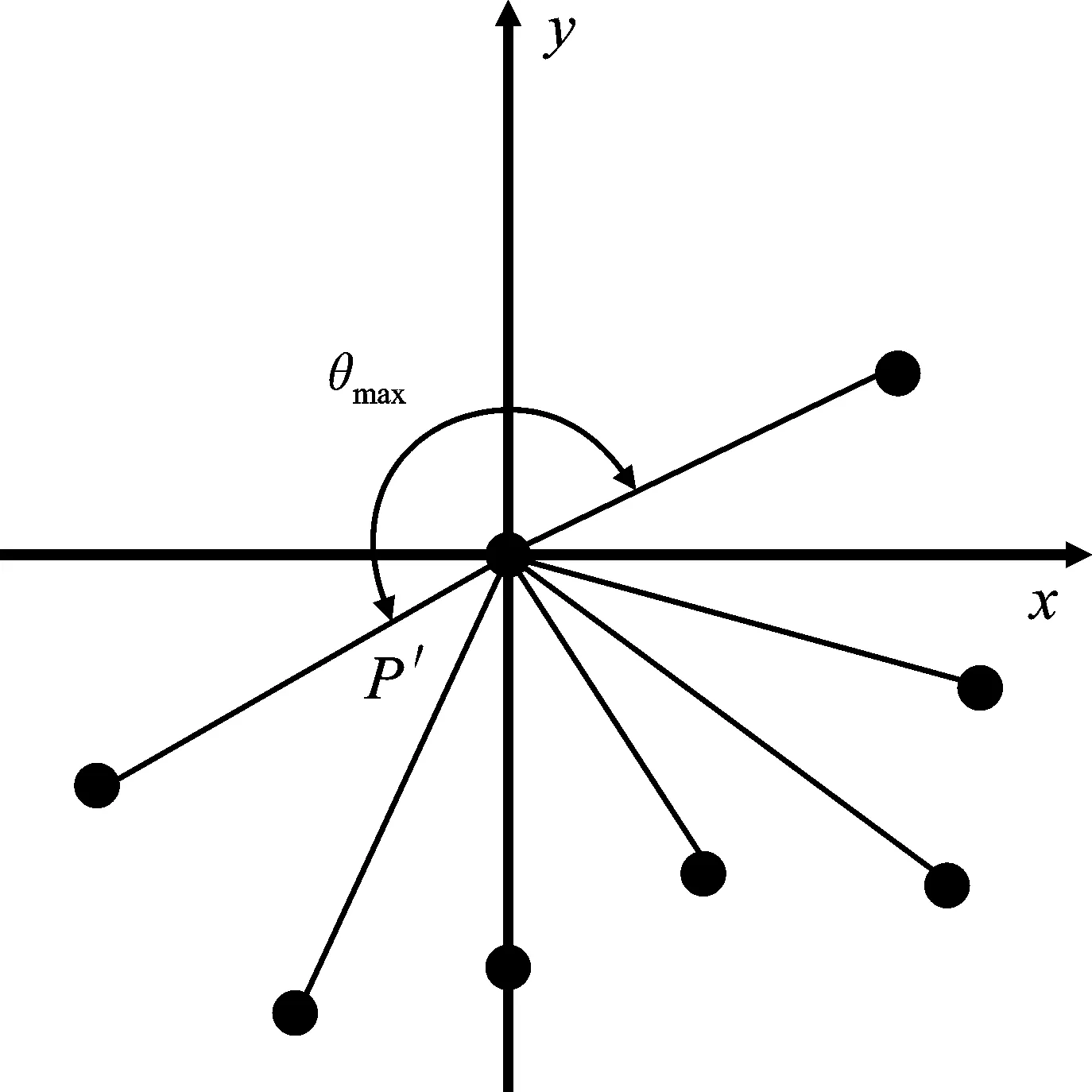
图5 P为边界点Figure 5.P is the boundary point

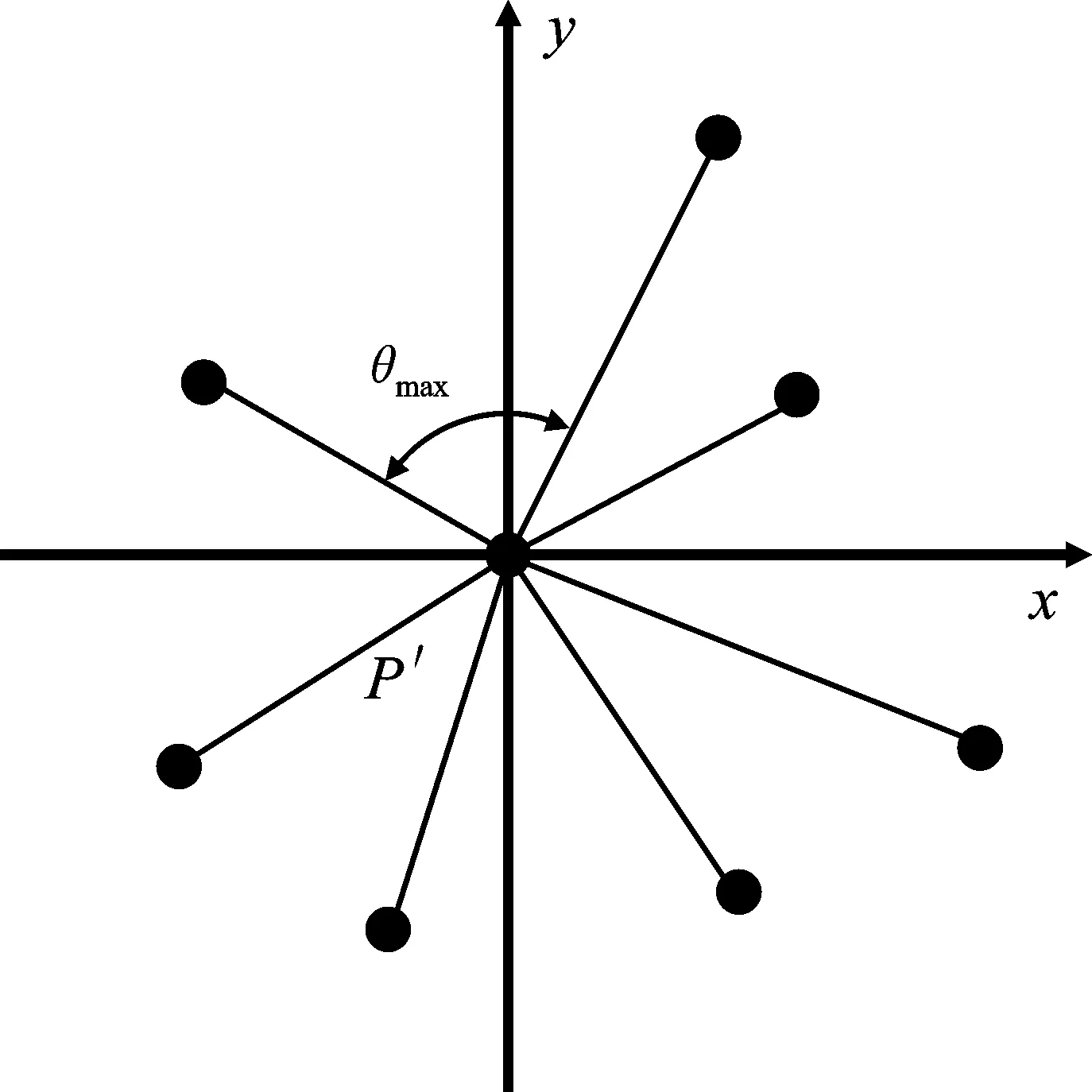
图6 P为内部点 Figure 6.P is the internal point

由图5和图6可以看出，当点P为边界点时，最大相邻夹角θmax比点P为内部点时大。根据这个特点，当最大相邻夹角θmax大于设定的阈值ε时，可以认为点P为边界点。为了求出最大相邻夹角θmax，需先求出所有相邻夹角的值。首先确定一个基准向量，然后求出每个向量与基准向量之间的夹角，记为基准夹角，再将相邻向量的基准夹角相减，即可得到相邻夹角，如图7所示。

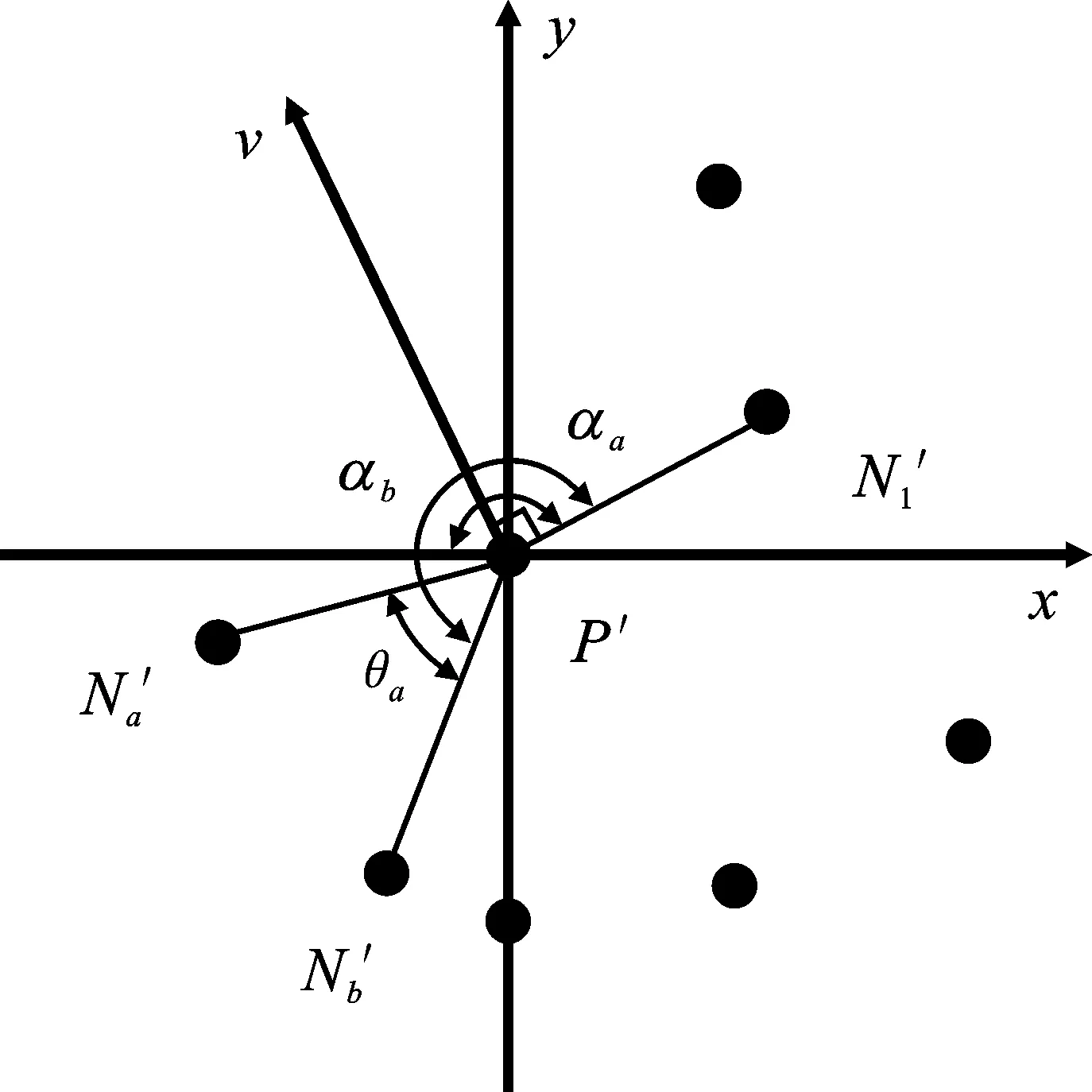
图7 相邻夹角的求解Figure 7. Solution of adjacent angle

如图7可以看出，P′N′1为基准向量，P′N′a(1≤a≤k)和P′N′b(1≤b≤k)为任意两个相邻向量。P′N′a与基准向量之间的基准夹角为αa，P′N′b与基准向量之间的基准夹角为αb，两者之差即为P′N′a和P′N′b的相邻夹角θa。

由于基准夹角的取值范围为0°～360°，而向量夹角计算式只能求解出0°～180°的劣角，所以要先对基准夹角的大小进行判断。

(4)

式中，P′N′1为基准向量；n为拟合平面的法向量；v为两者的叉积，方向遵守右手定则。当向量P′N′i(1≤i≤k)与v的夹角为锐角时，基准夹角为劣角；当与v的夹角为钝角时，基准夹角为优角。

基准夹角αi为向量P′N′i与基准向量P′N′1的夹角，其求解如式(5)所示。

(5)

最后，将所有基准夹角α的值从小到大依次排列得β1<β2<…<βk，即可算出所有相邻夹角θ的值，如式(6)。

(6)

通过比较可得到最大相邻夹角θmax。边界判断流程如图8所示。

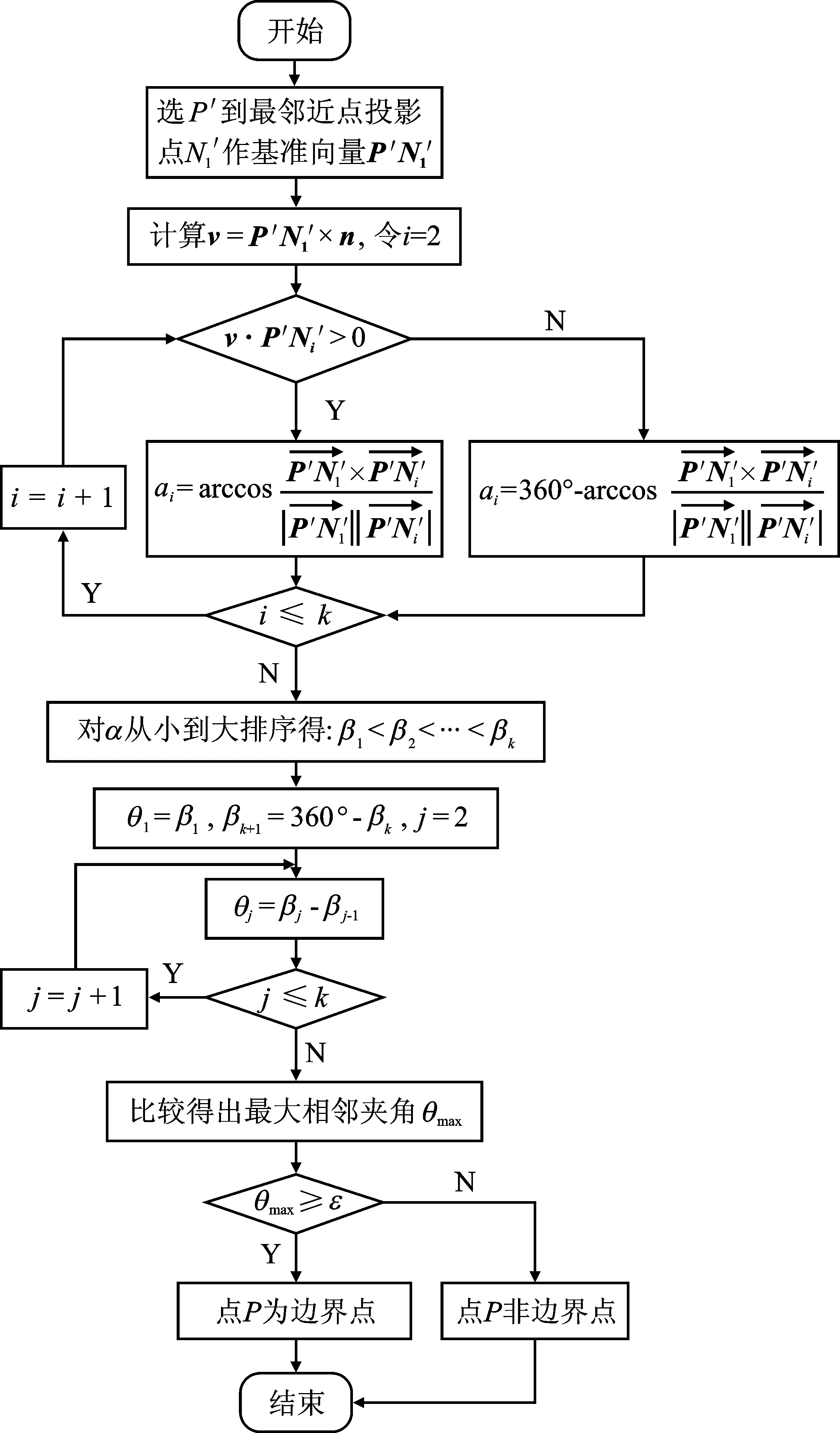
图8 边界提取算法流程图Figure 8. Flow chart of boundary judgment algorithm

3 点云边界质心处理方法

由于点云中每个数据点的质量相同且分布均匀，所以边界质心相对于点云边界的位置也是固定的。质量均匀的矩形质心在其对角线的交点，球的质心在球心。边界质心Pc的求解如式(7)所示。

(7)

从不同角度测量得到的点云数据所参照的坐标系不同，原始点云数据之间会存在较大的初始距离。如果点云之间的初始距离过大，重叠度过低，直接使用K-4PS算法对点云进行粗配准时，会出现对应点选取错误或运算时间过长等问题，降低粗配准的效率。计算并配准点云的边界质心能快速缩短初始位置距离，并增加点云之间的重叠度。为了尽量避免可能存在的噪声点对质心位置的干扰，本文采用配准边界质心的方法来取代传统直接配准原始点云数据质心的方法，以防止质心位置因受噪声点影响而发生偏离进而导致待配准点云的重叠度降低的问题。由于质心与边界位置的相对性，配准点云的边界质心能在一定程度上减小点云之间的平移误差。为了方便使用K-4PS进行粗配准，可先将源点云和目标点云的边界质心都移动到坐标原点。此时，平移矩阵T如式(8)所示。

T=[-xc,-yc,-zc]T

(8)

4 结果与分析

4.1 实验设计与环境说明

在传统配准误差算法中，通过计算源点云与目标点云之间所有对应点的欧式距离之和来判断算法的配准效果。这种评价方法只把点云配准前后的位置误差纳入判断标准，没有对点云的姿态误差给出评价。为了能够多角度的对粗配准误差进行分析，本文通过配准矩阵反求出平移距离和旋转角度，再把这些值与标准值进行对比，得出平移误差和旋转误差。为了方便比较粗配准前后点云之间的位姿关系，本文分别计算了3个坐标轴方向的平移和旋转误差，同时记录下每种算法完成粗配准所消耗的时间。通过精度和时间两个方面，对本文粗配准方法的效果进行了更加全面的评估。

在实际测量过程中，受被测物体大小和测量环境的限制，可能会出现一次测量只能得到物体部分点云数据的情况。为了测试本文粗配准方法的适用范围，特地选取两组完整点云Dinosaur、Horse和一组非闭合点云Bunny进行粗配准实验。选取的点云Horse只有平移误差，点云Dinosaur只有旋转误差，而点云Bunny既有平移误差又有旋转误差，这样就能测试本文方法对不同类型误差的配准效果，方便对误差做出分析。同时，本文选择在粗配准算法中配准速度较快的采样一致性初始配准算法(Sample Consensus Initial Alignment，SAC-IA)[18]和精度较高的传统K-4PCS算法与本文方法进行比较，来验证本文方法在速度和精度方面的优势。

本文实验所用计算机配置为：Intel Core i7-8750H 2.20 GHz CPU，8 GB内存，Windows 10 64位操作系统，实验代码通过Visual Studio 2017和PCL 1.8.1版本进行编译。

4.2 实验结果与分析

4.2.1 点云Dinosaur配准结果分析

完整点云Dinosaur一共有23 982个数据点，源点云与目标点云只有平移误差，分别使用3种方法对其进行配准实验，如图9所示。

由图9可以看出，本文方法的粗配准效果优于SAC-IA算法和传统K-4PCS算法。SAC-IA算法配准的点云Dinosaur在脖子处都出现了明显的偏移，传统K-4PCS算法也在脖子处出现了少量的偏移，本文方法配准的脖子处点云重合度最高。为了能够更加客观地对比实验结果，分别记录了旋转误差、平移误差和配准时间，结果如表1所示。

(a) (b)

表1 点云Dinosaur粗配准精度和时间对比Table 1. Comparison of accuracy and time of Dinosaur point cloud coarse registration

由表1可以看出，在粗配准精度方面，本文方法的平移精度约为SAC-IA算法的4.8倍，约为传统K-4PCS算法的1.6倍；旋转精度约为SAC-IA算法的9倍，约为传统K-4PCS算法的1.2倍。SAC-IA算法减少了点云平移误差，但又引入了大量的旋转误差，整体的配准效果不佳。传统K-4PCS算法旋转误差较小，但平移误差较大，配准效果稍逊本文方法。配准速度方面，本文方法的配准速度达到了SAC-IA算法的1.6倍，是传统K-4PCS的2倍以上。综上所述，本文算法在配准只有平移误差的完整点云Dinosaur时，在精度和速度方面都全面优于其他两种算法。

4.2.2 点云Horse配准结果分析

完整点云Horse一共有48 485个数据点，源点云与目标点云之间只有旋转误差，分别使用3种方法对其进行配准实验，如图10所示。

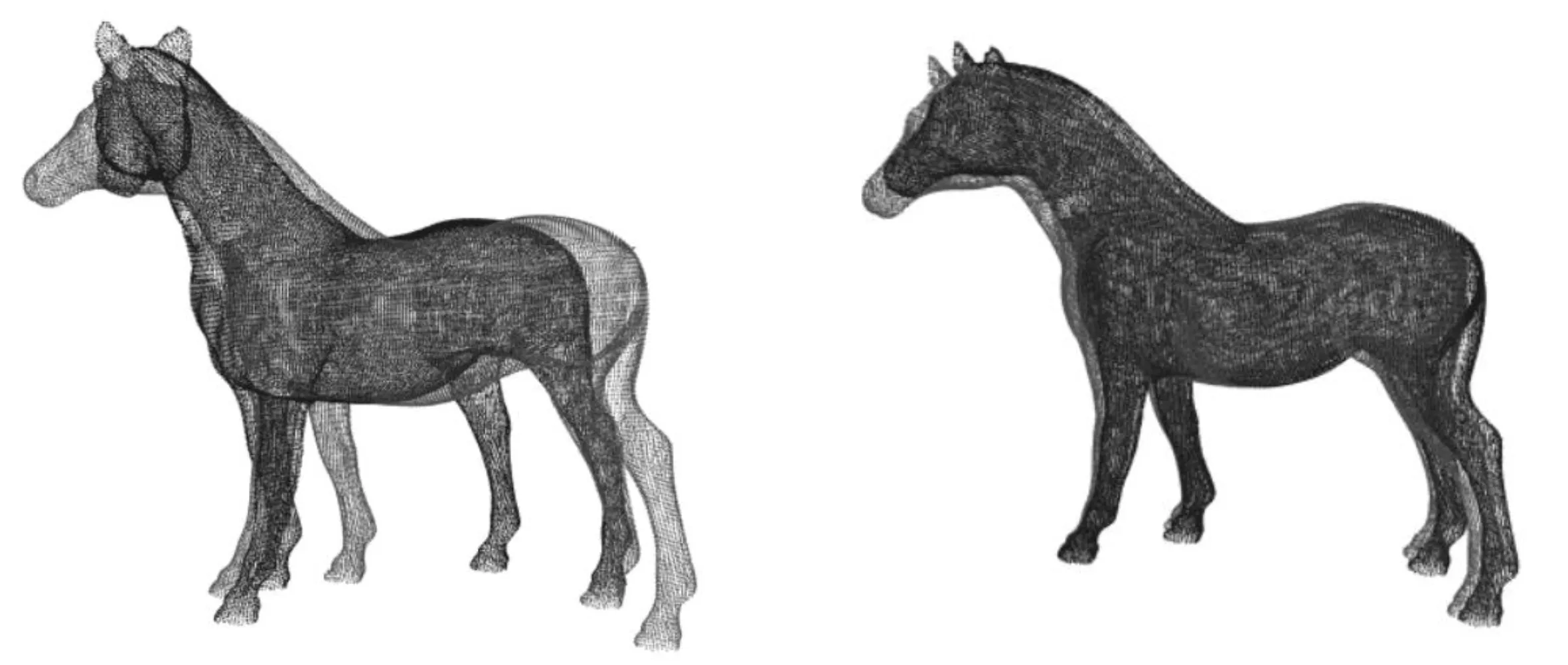
(a) (b)

由图10可以看出，本文方法和传统K-4PCS算法的粗配准效果都优于SAC-IA算法。SAC-IA算法配准的点云Horse在马的头部出现了大量的未配准点，马蹄部分也出现了明显的分离。传统K-4PCS算法和本文方法的配准效果良好，仅在马蹄处出现少量未配准点。为了能够更加客观地对比实验结果，本文分别记录了旋转误差、平移误差和配准时间，结果如表2所示。

由表2可知，在粗配准精度方面，本文方法的平移精度约为SAC-IA算法的5倍，与传统K-4PCS相当；旋转精度约为SAC-IA算法的4.5倍，为传统K-4PCS的2.7倍。在SAC-IA算法配准后，两点云之间还是存在着一定的平移和旋转误差，配准效果不佳。尽管传统K-4PCS算法平移精度与本文方法相当，但是其绕3个轴的旋转误差普遍都高于本文方法，导致整体配准精度稍逊于本文方法。在粗配准速度方面，本文方法配准速度是SAC-IA算法的1.3倍，是传统K-4PCS的1.6倍。实验证明，本文算法在配准只有旋转误差的完整点云Horse时，在精度和速度方面优于其他两种粗配准算法。

表2 点云Horse粗配准精度和时间对比Table 2. Comparison of accuracy and time of Horse point cloud coarse registration

4.2.3 点云Bunny配准结果分析

非闭合点云Bunny的目标点云有40 256个数据点，源点云有40 097个数据点，两个点云之间既有平移误差又有旋转误差，分别使用3种方法对其进行配准实验，配准结果如图11所示。

(a) (b)

由图11可知，本文方法的粗配准效果依然优于SAC-IA算法和传统K-4PCS算法。SAC-IA算法配准的点云Bunny在背部、尾部和耳朵部分出现了较多的未配准点。传统K-4PCS算法配准的点云整体上有少许旋转偏移，耳朵部分点云的重合度偏低。本文方法配准的点云重合度较高，点云之间没有明显的平移和旋转偏移，特别是兔子耳朵部分点云的配准效果好于其它两种方法。为了能够更加客观的对比实验结果，分别记录了旋转误差、平移误差和配准时间，结果如表3所示。

由表3可知，在粗配准精度方面，本文方法的平移精度约为SAC-IA算法的6倍，为传统K-4PCS的1.8倍；旋转精度约为SAC-IA算法的5倍，为传统K-4PCS的1.4倍。由于非闭合点云Bunny的源点云和目标点云的数据点个数不同，存在着大量噪声点，导致SAC-IA算法的平移精度和旋转精度都较低，配准效果相对一般。传统K-4PCS也因为噪声点的干扰，与本文方法的精度差距被稍稍拉大，但总体配准效果较好。而本文方法由于采用了边界提取算法，剔除了大量的噪声点，边界质心的配准保障了点云之间的高重叠度，所以在配准非闭合点云时，依旧保持了较高的精度。在粗配准速度方面，本文算法的配准速度是SAC-IA算法的1.6倍，是传统K-4PCS的2.2倍。所以，对于同时存在平移误差、旋转误差和噪声点的非闭合点云Bunny，与其他两种粗配准算法相比，本文算法的配准效果具有较大的优势。

表3 点云Bunny粗配准精度和时间对比Table 3. Comparison of accuracy and time of Bunny point cloud coarse registration

5 结束语

本文提出了一种基于点云边界质心的粗配准方法。该方法通过边界提取和边界质心配准，在加快粗配准速度的同时保障配准了点云粗配准的精度。选用两种常用粗配准方法作为参照，选取存在平移和旋转误差的3组完整和非闭合点云进行对比实验，并对实验结果进行了分析。实验结果证明，本文提出的粗配准方法是一种高效率、高精度、抗干扰性较强的粗配准方法。下一步将对点云精配准的加速和点云三维重建方面开展研究工作。依托于计算机技术的告诉发展和硬件设备的升级，实时同步进行三维测量、点云数据处理和三维重建的设备变得未来可期。基于此，在保证点云配准高精度的同时，提高配准的速度变得尤为重要。5G技术的发展为实时三维重建技术的应用渠道创造了可能，实时高效的三维重建技术的社会化应用也将更加广泛。