基于RRAM双交叉阵列结构的三值存内逻辑电路设计

刘维祎，孙亚男，何卫锋

(上海交通大学 电子信息与电气工程学院，上海 200240)

随着计算数据爆发式增长，传统的冯诺依曼架构开始面临存储墙的问题，即存储器与处理器之间大量数据搬运消耗了系统中大部分功耗并增加了系统延时[1-10]。传统的数字处理系统是二值的，逻辑值通过两个离散的电压表示。在处理大量数据时，二值系统的速度更加缓慢。此外，随着半导体器件特征尺寸的缩小，传统基于CMOS硅工艺的半导体器件亚阈值漏电流急剧增加[11-14]，基于CMOS的逻辑电路开始遇到物理瓶颈。因此，急需一种在解决存储墙问题的同时可以更高效地执行逻辑和算术运算的高性能计算范式，以应对未来数据密集型任务。

新型非易失存储器，例如阻变存储器(Resistive Random-Access Memory，RRAM)具有数据多值存储的能力[3]，同时也可用于逻辑计算[4-10]。如图1(a)所示，RRAM是一种由金属层、氧化物层和金属层组成的三明治结构器件。通过导电细丝的生长与破坏，RRAM可实现电阻大小的变化。如图1(b)所示，RRAM的阻值变化通过复位和置位过程实现。对于传统的单值RRAM而言，只存在高阻和低阻两种状态，而多值RRAM具有两个以上的阻值状态。在RRAM两端施加复位电压(负极电平高于正极)，导电细丝被破坏，RRAM阻值由低阻变为高阻。在RRAM两端施加置位电压(正极电平高于负极)，导电细丝生长，RRAM阻值由高阻变为低阻。

图1 RRAM器件原理(a)RRAM的三明治结构图 (b)单值RRAM与多值RRAM示意图Figure 1. The device principle of RRAM(a)The sandwich structure of RRAM(b)Single level cell RRAM and multi-level cell RRAM

逻辑计算可以在高密度集成的RRAM交叉阵列中实现，即存内逻辑电路。存内逻辑电路可以消除传统冯诺依曼架构中因数据搬运导致的功耗和延时开销。目前基于RRAM存内逻辑电路的设计，例如IMPLY(Material Implication)[4-7]和MAGIC(Memristor Aided Logic)[8-10]，只实现了二值逻辑操作，逻辑电路的输入和输出均通过交叉阵列中单值RRAM阻值表示。IMPLY和MAGIC仅支持一种基本二值逻辑操作，同时为了确保逻辑操作的正确性，无法提供多个扇入或扇出。另外，在RRAM交叉阵列中实现IMPLY和MAGIC逻辑电路时，逻辑电路的输入与输出需要在同一个交叉阵列的同一行或同一列上。在将任意二值逻辑函数映射到交叉阵列中时，基于IMPLY和MAGIC的映射方法[4-10]需要更多的拷贝操作来完成逻辑操作输入与输出的对齐。因此在传统的IMPLY和MAGIC二值存内逻辑电路中实现一个复杂的逻辑函数往往需要较多的操作步数以及较大的延时。

相比于二值逻辑系统，三值逻辑系统可以减少算术运算所需要的位数，从而减少逻辑操作数目并降低计算复杂度。新型的纳米技术如碳纳米晶体管(Carbon Nanotube MOSFET，CN-MOSFET)具有较低的漏电流以及可变的器件大小[11-14]。通过调节平带电压实现的多阈值CN-MOSFET可以用来实现三值逻辑电路[14]。然而，以往的三值逻辑电路设计多基于传统的冯诺依曼系统。三值存内逻辑电路的实现仍是一个很大的挑战。

本文提出了一种新型的基于RRAM双交叉阵列结构的三值存内逻辑电路设计。在该设计中，逻辑电路的输入和输出均通过多值RRAM的阻值表示。CN-MOSFET与RRAM可以通过三维的方式进行异质集成[11]。为了构建高密度集成且低能耗的三值存内逻辑电路系统，外围电路由CN-MOSFET实现。本文提出的电路结构支持两种可具有多个扇入和扇出的三值逻辑门以及一种Material Implication逻辑门。基于以上的两种三值逻辑门和一种Material Implication逻辑门，任意三值逻辑函数可以快速地映射到交叉阵列结构中。本文将基于不同存内逻辑电路设计的多位行波进位加法器进行了实现。实验结果表明，相比于传统二值存内逻辑电路设计，三值存内逻辑电路加法器可以减少68.84%的操作步数。相比于传统IMPLY电路设计，三值存内逻辑电路加法器可以降低33.05%的能耗。

1 基于RRAM双交叉阵列结构的三值存内逻辑电路设计

图2为RRAM双交叉阵列结构。在三值存内逻辑电路中，RRAM的高阻状态表示逻辑“0”；中间阻值状态表示逻辑“1”；低阻状态表示逻辑“2”。图2所示的电路结构支持两种三值逻辑门(MAX以及NMAX)，以上两种逻辑门可支持多个扇入和扇出。此外，该电路结构还支持NIMP逻辑门[7]。

1.1 三值逻辑门MAX与NMAX的电路设计

根据多值逻辑代数学，三值逻辑门MAX、NMAX以及一些一元运算符可以组成三值逻辑函数的全集[15]。一元运算符根据文献[13]通过外围CN-MOSFET逻辑电路实现，三值逻辑门MAX与NMAX则通过RRAM双交叉阵列结构实现。MAX与NMAX的真值表如图3所示。MAX与NMAX逻辑门电路如图4所示。MAX与NMAX逻辑门可以直接映射到图2所示的RRAM双交叉阵列结构中。在将MAX与NMAX逻辑门映射到双交叉阵列结构中时，逻辑门的输入在一个交叉阵列的同一列，逻辑门的输出在另一个交叉阵列中。

图2 RRAM双交叉阵列结构Figure 2. The proposed RRAM dual-crossbar structure

图3 MAX与NMAX逻辑门真值表Figure 3. The truth table of MAX and NMAX gates

下面以MAX逻辑门为例说明三值存内逻辑电路的工作原理。三值逻辑门的输入值以阻值的形式存储在输入RRAM(A和B)中，输出RRAM在操作前先初始化为高阻状态。通过施加外围电压Vcond和VWR，电路开始进行逻辑计算。输入RRAM和参考电阻(RT)形成分压结构并驱动后一级的标准反相器(Standard Ternary Inverter，STI)电路。考虑到CN-MOSFET的高驱动强度以及较小的面积，STI电路通过CN-MOSFET实现，以便最大限度保留RRAM交叉阵列结构的高速翻转和高密度集成特性。

STI电路如图5所示。通过调整CN-MOSFET的平带电压(Vfb)，STI电路可输出3种离散的电压值(Vso)。如图4所示，Vso驱动1T1R结构中P型CN-MOSFET的栅极。不同的Vso电压值可以调节流过1T1R结构的限制电流。根据不同的输入情况，输出RRAM或者维持在高阻状态，或者翻转到的中间阻值状态或低阻状态。

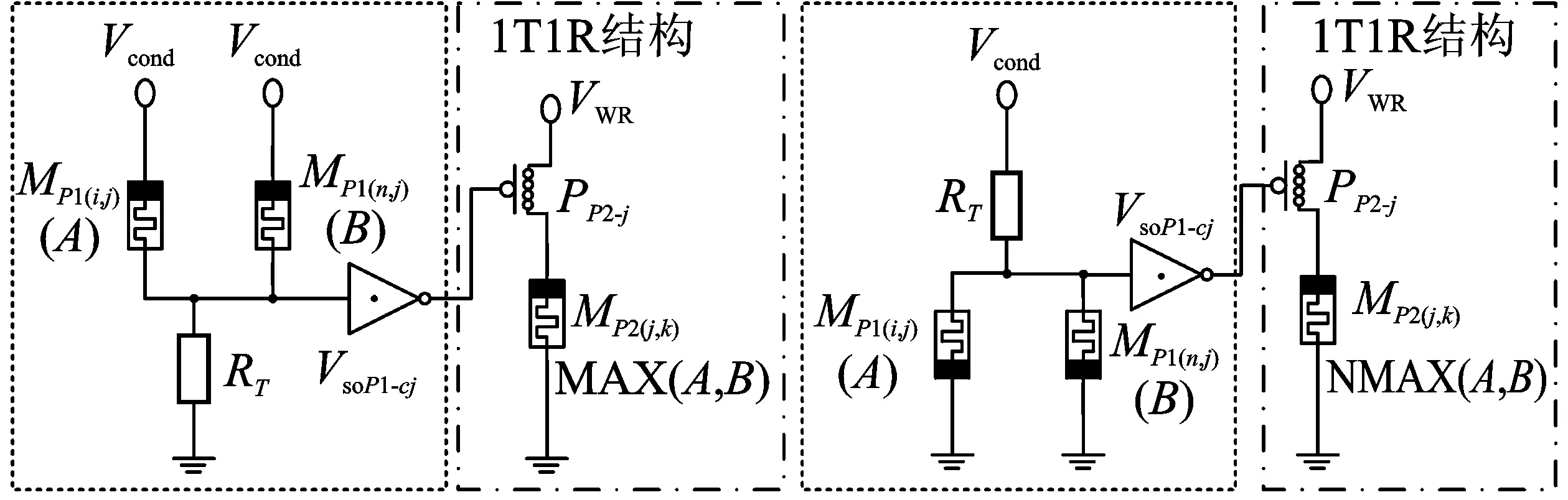
图4 MAX与NMAX逻辑门电路图(a)MAX逻辑门电路图 (b)NMAX逻辑门电路图Figure 4. The circuit schematic of MAX and NMAX(a)The circuit schematic of MAX gate (b)The circuit schematic of NMAX gate

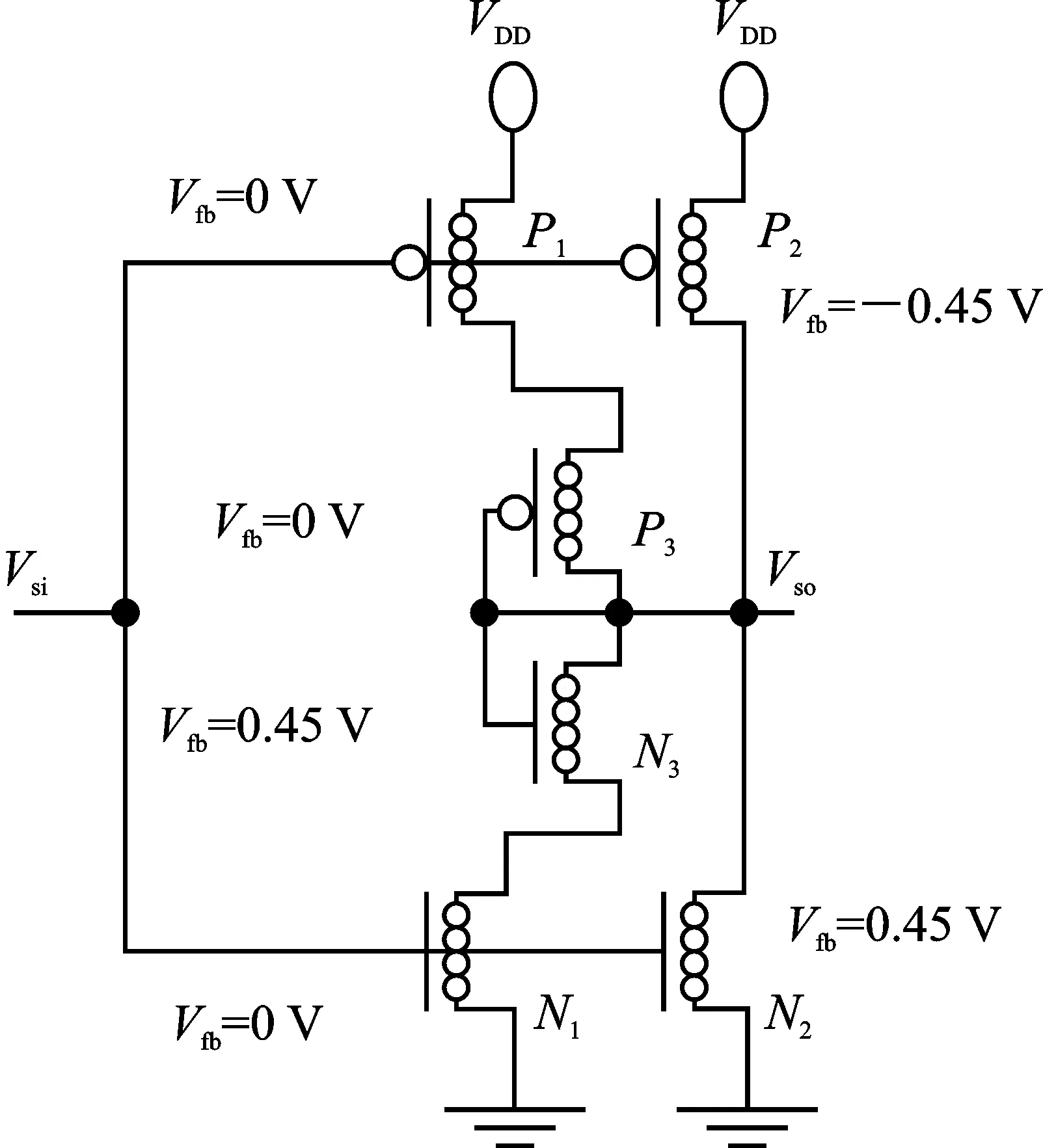
图5 STI电路图Figure 5. The circuit schematic of STI

MAX逻辑门的仿真波形如图6所示。HSPICE的仿真基于Verilog-A RRAM模型[16]和16nm Stanford University Virtual Source GAA-CN-MOSFET模型[17-18]。CN-MOSFET电路供电电压为0.7 V。RRAM的高阻状态的阻值为1 MΩ，低阻状态阻值为5 kΩ[16]。Vcond电压为0.7 V，1T1R结构中的VWR电压为1.3 V。在存在工艺偏差时，为了保证在不同输入情况下输出RRAM仍可以正确地翻转到希望阻值状态，参考电阻RT选取阻值为35 kΩ，RRAM中间阻值状态选取阻值为60 kΩ。当两个输入RRAM均处于高阻状态(逻辑“0”)时，输出RRAM维持在高阻状态(逻辑“0”)，如图6(a)所示。当输入RRAM有一个为低阻状态(逻辑“2”)时，输出RRAM翻转到低阻状态(逻辑“2”)，如图6(b)所示。其余情况下，输出RRAM翻转到中间阻值状态(逻辑“1”)，如图6(c)所示。

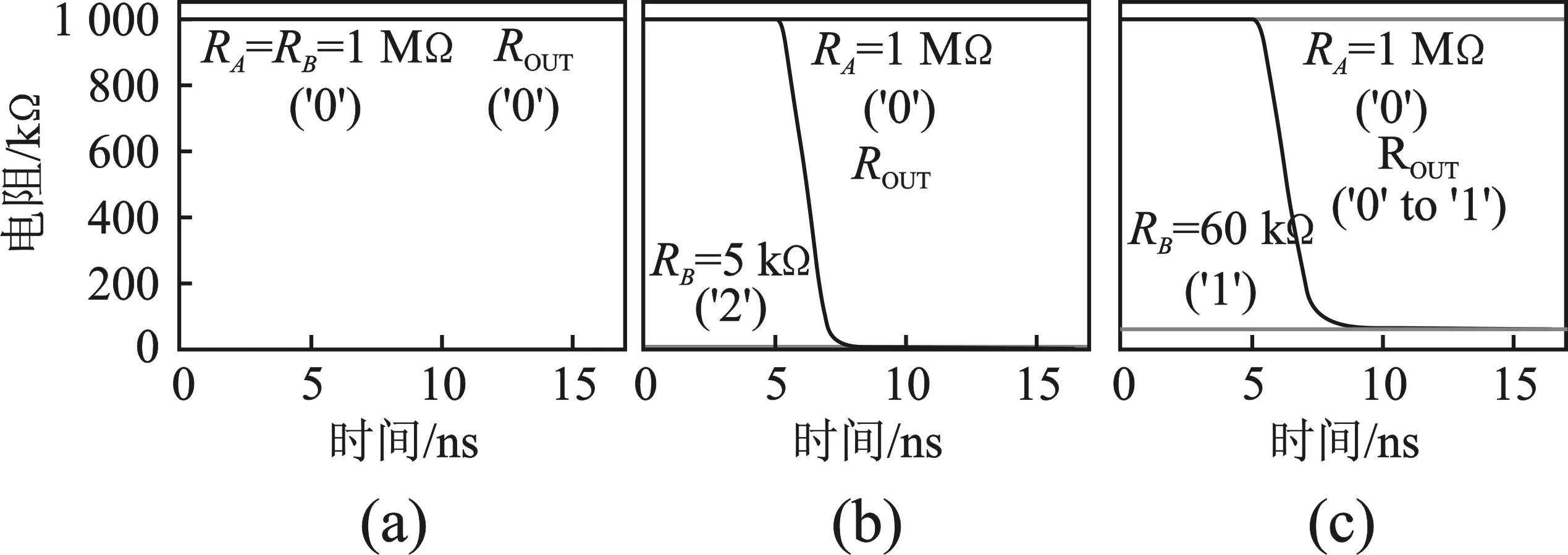
图6 MAX逻辑门仿真波形(a)输入RRAM均为高阻状态时的仿真波形(b)输入RRAM有一个为低阻状态时的仿真波形(c)输入RRAM分别为高阻状态和中间阻值状态时的仿真波形Figure 6. The simulation waveform of MAX gate(a)The simulation waveform when the inputs are in high resistance state (b)The simulation waveform when one of the inputs is in low resistance state (c)The simulation waveform when the inputs are in high resistance state and medium resistance， respectively

在三值存内逻辑电路设计中，当多个MAX或NMAX逻辑门的输入位于一个交叉阵列的不同列且对齐时，多个MAX或NMAX逻辑门可以并行执行，多个逻辑门的输出位于另一个交叉阵列的同一列中。另外，通过将MAX与NMAX逻辑门的输入RRAM和输出RRAM分离在不同的交叉阵列中，本文提出的MAX与NMAX逻辑门可支持多个扇入和扇出。通过调整Vcond电压值的大小可以实现多个扇入，通过调节VWR电压值的大小可以实现多个扇出。因此，三值存内逻辑电路设计避免了以往二值存内逻辑电路设计中由于拷贝操作过多造成的延时开销。在将任意一个逻辑函数映射到交叉阵列结构时，基于三值存内逻辑电路结构的实现方式具有更快的计算速度。

1.2 NIMP门的电路设计

除了章节1.1中讨论的三值MAX和NMAX逻辑门外，本文提出的电路结构支持一种Material Implication逻辑门，称为NIMP[7]。NIMP门的输入RRAM与输出RRAM均位于同一个交叉阵列中。NIMP门的真值表如图7(a)所示。NIMP门可以在双交叉阵列结构的任一交叉阵列中实现。NIMP门包含两个RRAM器件(p和q)以及一个参考电阻RB。原始输入以阻值的形式存储在RRAM器件p和q中。施加Vcond+和Vcond-后电路开始工作，逻辑门输出值以阻值的形式存储到RRAM器件q中。

图7 NIMP门的实现 (a)NIMP门真值表 (b)输入位于同一列的NIMP门电路 (c)输入位于同一行的NIMP门电路Figure 7. NIMP gate implementation (a)The truth table of NIMP gate (b)The circuit of NIMP gate when the inputs are in the same column of crossbar (c)The circuit of NIMP gate when the inputs are in the same row of crossbar

2 与其他二值存内逻辑电路设计的对比

本文将基于不同存内逻辑电路设计的多位行波进位加法器进行了实现。基于文献[10]中的compact mapping方法与文献[6]中的semi-parallel方法分别实现了64位二值行波进位加法器。为了公平地比较，三值行波进位加法器的位数进行了相应的调整以保证和二值行波进位加法器的和的范围相近。由于41位三值行波进位加法器与64位二值行波进位加法器的和的范围相近，因此其被选作比较对象。

表1中对不同加法器设计的操作步数以及能耗进行了比较。二值行波进位加法器的位数表示为Nb。在基于MAGIC的Compact Mapping方法中[10]， MAGIC逻辑电路设计只支持NOR2门以及NOT门。所有的原始输入被映射到交叉阵列的同一列中，之后将NOT门与NOR2门映射到交叉阵列中。为了将逻辑门的输入对齐在交叉阵列的同一行或同一列中，Compact Mapping法需要很多的拷贝操作。对于Nb位的二值行波进位加法器，Compact Mapping方法共需要(13Nb+4)步操作。

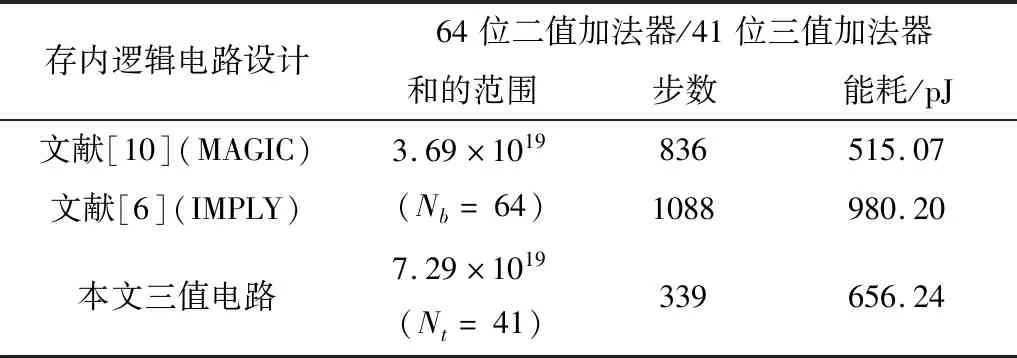
表1 存内逻辑电路实现加法器的对比Table 1. Comparison of logic-in-memory adders

在基于IMPLY的semi-parallel加法器设计中，不同全加器之间的操作需要串行执行，每一个全加器可以在交叉阵列的两行中并行执行[6]。由于在基于Semi-parallel的加法器设计中，大部分操作仍然是串行执行的，因此其相比于MAGIC设计具有更多的操作步数。对于Nb位的二值行波进位加法器，Semi-parallel方法共需要17Nb步操作。

三值存内逻辑电路加法器设计如下所示：首先构建三值全加器，A、B和Cin是三值全加器的输入。S和Cout是三值全加器的输出。A、B和S的取值范围为{0, 1, 2}。Cin和Cout的取值范围为{0, 2}。计算S和Cout所需的一元运算符的真值表如表2所示。

表2 一元运算符真值表Table 2. The truth table of unary operators

(1)

(2)

根据式(1)及式(2)以及本文电路结构所支持的MAX、NMAX和NIMP逻辑门可以构建三值全加器多层逻辑网络图，如图8所示，实现Nt位加法器的步数已在图上标出。三值行波进位加法器的位数表示为Nt。在将Nt位三值行波进位加法器映射到RRAM双交叉阵列结构中时，首先将由CN-MOSFET外围电路[13]产生的一元运算符逻辑值写入到Plane-1和Plane-2相应的RRAM中。两个交叉阵列中的一元运算符需要对齐以最大化NIMP操作的并行度。生成所有Nt位的NIMP逻辑门结果一共需要7步。NIMP逻辑门的结果需要在同一列中以便进行MAX操作，产生所有Nt位的G1～G5结果一共需要2Nt步。通过G1～G4与Cin做NIMP操作得到每一个三值全加器的H1～H5；通过G5与H5做MAX操作得到每一个三值全加器的Cout。产生Nt位加法器最后进位结果需要(5Nt+2)步。产生最后的和的结果需要(Nt+2)步。因此完成Nt位加法器的映射一共需要(8Nt+11)步。

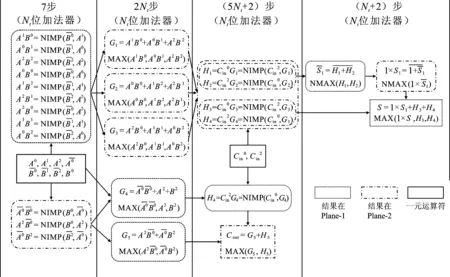
图8 三值全加器多层逻辑网络图Figure 8. The multi-level logic network for implementing a ternary full adder

如表1所示，相比于64位MAGIC二值存内逻辑电路加法器，41位三值存内逻辑电路加法器可以减少59.45%操作步数。相比于64位IMPLY二值存内逻辑电路加法器，41位三值存内逻辑电路加法器可以减少68.84%操作步数。相比于二值逻辑，三值逻辑具有更少的位数以及更少的逻辑操作数目，因此三值存内逻辑电路加法器具有最快的计算速度。

三值存内逻辑电路加法器速度提升的代价为其能耗相比于MAGIC二值存内逻辑电路设计多出了27.41%。相比于IMPLY二值存内逻辑电路设计，三值存内逻辑电路加法器能耗降低了33.05%。

3 结束语

本文提出了一种新型的基于RRAM双交叉阵列结构的三值存内逻辑电路设计。在三值存内逻辑电路设计中，逻辑函数的输入与输出值均通过多值RRAM的阻值状态表示。该电路结构支持两种可具有多个扇入和扇出的三值逻辑门以及一种Material Implication逻辑门。本文将基于不同存内逻辑电路设计的多位行波进位加法器进行了实现。实验结果显示，相比于传统二值存内逻辑电路设计，三值存内逻辑电路加法器可以提升高达68.84%的计算速度。相比于传统IMPLY逻辑电路设计，三值存内逻辑电路加法器可以降低33.05%能耗。