基于VMD和BP神经网络的轨道病害诊断方法
华 莉,杨 俭,袁天辰,宋瑞刚
(上海工程技术大学 城市轨道交通学院,上海 201620)
随着我国高速铁路的快速发展,铁路运营里程逐年增加。截止2019年,我国在运营的高铁总里程达到35 000 km,预计到2025年将达到38 000 km。中国已成为世界上拥有最大铁路网和最完善高铁系统的国家[1]。然而,随着运营时间和运营里程的增加,轨道层级结构病害时有发生,严重威胁着我国高铁线路的运行安全。目前,轨道结构检测技术的发展仍处于比较滞后的地步,国内外主要依靠人工目视检查和手动探伤来进行轨道结构检测,该方法效率低、风险大且漏检率高[2]。随着人工智能、大数据和无线传感网络技术的发展,高速铁路轨道层级结构服役状态智能监测和故障识别分类已经成为一个重要的研究方向。文献[3]提出利用塑料光纤传感器对列车轨道结构中的疲劳裂纹进行实时监测,并进行故障诊断和跟踪其演变。文献[4]基于RS-BN算法对轨道电路故障进行诊断。利用智能算法保证铁路运行的安全已成为了一项重要课题。
目前,用于处理非线性和非稳态振动信号的方法主要有变分模态分解(Variational Mode Decomposition,VMD)、经验模态分解(Empirical Mode Decomposition,EMD)、小波变换(Wavelet Transform,WT)和局部均值分解(Local Mean Decomposition,LMD)等[5-8]。其中,EMD、WT、LMD等方法都属于递归式算法,在对振动信号进行分解的过程中,可能会由于过分解而产生模态混叠和端点效应现象。VMD是一种新型信号分解方法,不属于递归式算法。VMD方法的目的是将样本信号分解成不同频率的子信号,并且可以自适应地根据实际需要将原始信号分解成若干个本征模态函数(Intrinsic Mode Function,IMF),通过自动匹配每个模态分量的中心频率和带宽实现IMF的分离,从而有效分解原始信号[9]。与其他方法相比,VMD方法具有更好的抗噪性,并且能够较好地解决信号分解过程中可能出现的模态混叠问题。此外,其端点效应现象也低于其他方法[10]。
在振动信号的特征提取方面,针对复杂时间序列随机性和动力学突变问题的检测,文献[11]提出了排列熵(Permutation Entropy,PE)算法。PE算法的计算较为简单,所需时间较短,即使是在含有噪声的复杂环境中,也能够发挥较好的检测作用,且具有良好的鲁棒性。多尺度排列熵(Multi-scale Permutation Entropy,MPE)算法则在排列熵的基础上融入多尺度化理论,通过对待检测的时间序列粗粒化计算,实现主要故障信息特征的有效提取[12]。本文通过将多尺度和排列熵理论相结合,以期多方面、多维度地提取轨枕病害信号的特征信息。
本文针对轨枕信号属于非线性、非稳态信号的特点,同时考虑到传感器退化等原因引起的故障特征区分度不高的缺陷,提出一种基于VMD和BP神经网络的轨道病害诊断方法。首先利用VMD算法对轨枕信号进行分解,得到若干个IMF,以实现对样本信号的降噪和主要故障信息的提取。然后通过MPE算法计算各IMF的特征值,得到多组排列熵,形成多尺度的高维特征向量,实现对轨道病害特征的提取。最后,建立基于BP神经网络算法的轨道病害诊断模型,将高维特征向量作为BP神经网络的输入,通过网络训练验证实现对轨道病害的识别及诊断。
1 基本原理
1.1 变分模态分解
文献[13]提出了一种自适应信号分解方法,即VMD。该方法属于完全非递归式的信号分解方法。VMD的分解过程是利用重复计算来寻求模型的最优解,通过合理分配每个分量信号的中心频率来有效地分离每个分量,从而确定各模态分量的中心频率和带宽[14]。实际上,VMD算法的分解过程是对样本信号的变分求解过程,目的是使每个模态分量的估计带宽的和达到最小,同时要满足模态之和等于原始信号的条件。基于交替方向乘子算法对每个模态及相应的中心频率进行连续更新,最后通过将各模态逐步解调到对应的基频带,从而提取各模态分量及其中心频率。
VMD主要流程如下[15]:
对振动信号进行模态分解,求得每个模态分量的信号uk(t)。通过Hilbert变换法计算出样本信号,求得所对应的单边频
(δ(t)+j/πt)·uk(t)
(1)
通过加入指数项e-jωkt,对各模态分量信号的中心频率进行估计,将经分解后所得的IMF的频谱转换到对应的基带
[(δ(t)+j/πt)·uk(t)]e-jωkt
(2)
利用高斯平滑偏移信号对各子信号的带宽进行估算,从而构建变分问题
(3)
(4)
其中,uk是经分解后的模态分量信号;ωk是被分解后的各模态分量信号对应的中心频率;f为原始信号;t为时间;δ(t)为脉冲函数;j为虚数单位。
⑲㉚㊷蒋介石:《自述研究革命哲学经过的阶段》(1932 年 5 月16日),秦孝仪主编:《先总统蒋公思想言论总集》第10卷,(台湾)国民党“中央党史会”1984年版,第539、538、534页。
为解决变分问题,通过构造拉格朗日函数,引入二次惩罚因子α和拉格朗日乘子算子λ(t),得到拓展后的拉格朗日表达式为
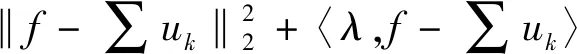
(5)
经过多次迭代计算,搜索拉格朗日表达式的最小值得到最优的解,最优解为uk和中心频率ωk。VMD算法的主要流程如图1所示。
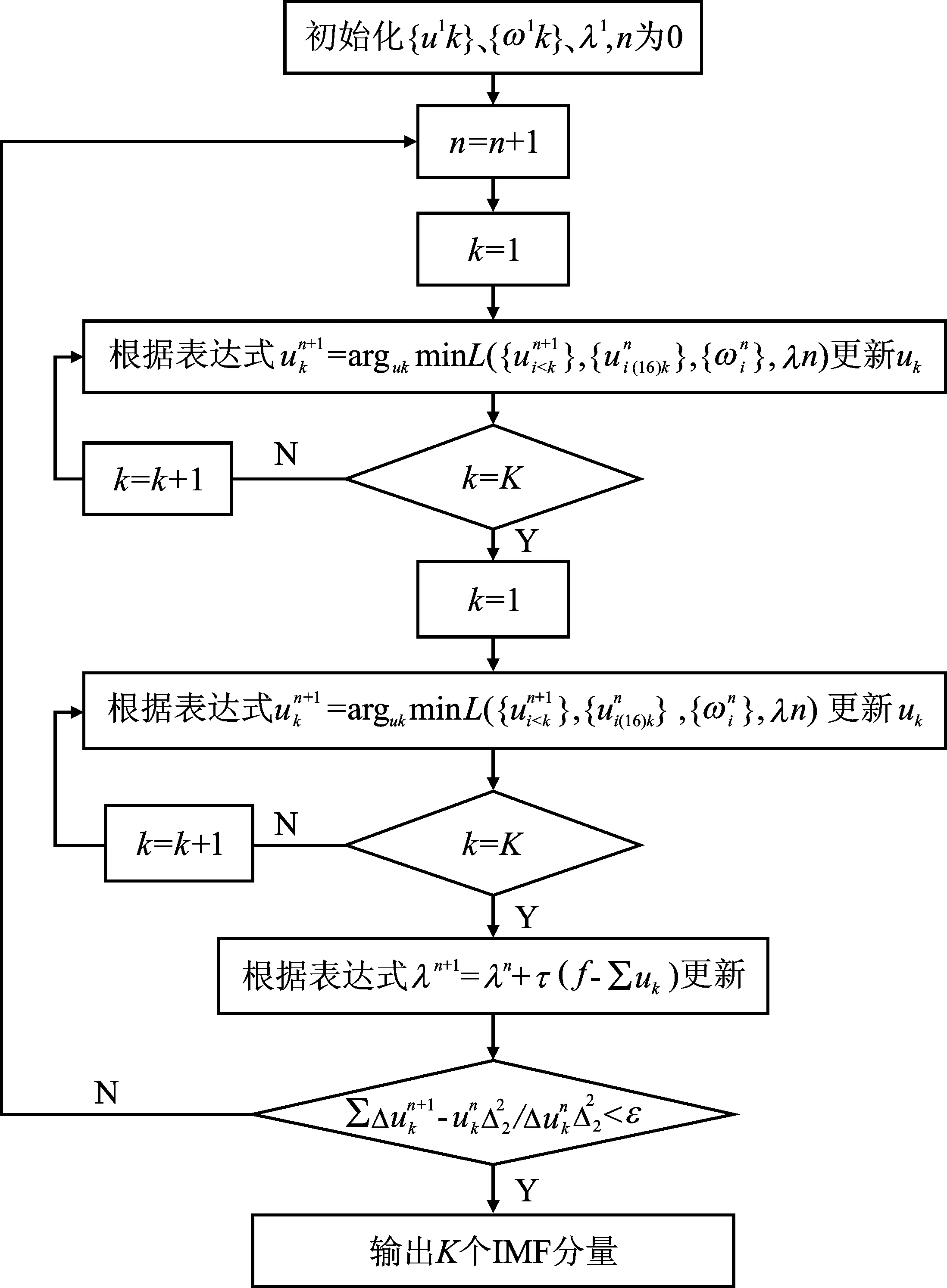
图1 VMD流程图Figure 1. Flow chart of VMD
1.2 BP神经网络
BP神经网络是一种典型的多层前向型神经网络[16-17]。该算法的实质是通过正反向传播来寻找误差函数的最小值,根据误差函数具有负梯度方向的特点来修改加权因子。其通常采用非线性规则中的最速梯度下降法[18]。该算法通过储存大量输入与输出数据,并对输入和输出之间的映射关系进行表达,已成为应用最广泛的人工神经网络系统。BP神经网络的结构如图2所示。

图2 BP神经网络结构图Figure 2. Structure diagram of BP neural network
由图2可知,BP神经网络的模型结构由输入层、隐含层和输出层组成,上层和下层之间通过节点连接。当信号从输入层进入后,将向前继续传播,直至到达隐含层。输入信号在隐含层经过不同的函数计算处理之后,会继续向下进行传播,直至最终达到输出层。进入到输出层后即可对轨道常见的病害进行识别及诊断。
2 算法流程
本文提出的基于VMD和BP神经网络结合的病害诊断方法的主要步骤如下:
步骤1根据布置的加速度传感器采集得到轨枕振动加速度信号;
步骤3利用MPE算法计算各IMF的值,组成高维特征向量;
步骤4构建BP神经网络模型,选择训练和测试样本;
步骤5进行病害识别及诊断。
本文提出的病害诊断方法流程如图3所示。

图3 病害诊断流程图Figure 3. Flow chart of disease diagnosis
3 实验分析
3.1 信号仿真
为了验证VMD分解信号的有效性,通过构建一个仿真信号w,分别利用EMD和VMD方法对其进行分解,如图4和图5所示。
w=v1+v2+v3+0.1randn(size(v1))
0.1randn(size(cos(2π·2t)))
(6)
由图4可以发现,仿真信号经EMD分解后,在第3和第4个分量中产生了过分解导致的模态混叠现象。由图5对比可知,VMD分解有效分离了所给的仿真信号,没有出现模态混叠现象,有效避免了EMD所存在的问题。因此,本文采用VMD方法对轨枕振动信号进行预处理。
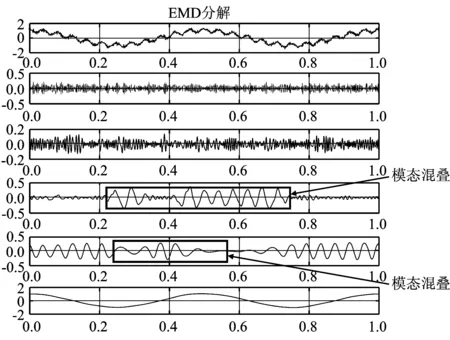
图4 EMD分解结果Figure 4. The decomposition result of EMD

图5 VMD分解结果Figure 5. The decomposition result of VMD
3.2 特征提取
本文从轨道结构振动响应出发,基于文献[19]提出的车辆-轨道耦合动力学理论,建立轨道层间结构动力学模型。通过传感器测得轨枕振动加速度数据,从而采集得到轨道结构振动信号信息。
针对从非线性和非稳态的轨枕振动信号提取病害特征较为困难的问题,本文提出基于VMD-MPE的病害特征提取方法。通过加速度传感器采集得到轨枕4种服役状态的数据信号(正常、道床板结、道床翻浆、轨枕空吊),经VMD分解后得到一系列IMF分量,然后通过计算各IMF分量的MPE值,实现对病害特征的提取。本文以114号轨枕为例,对振动信号进行VMD分解,设置采样频率为12 kHz,数据长8 000点,模态个数K为5,惩罚因子α为2 000。轨枕4类服役状态的VMD分解结果如图6所示。
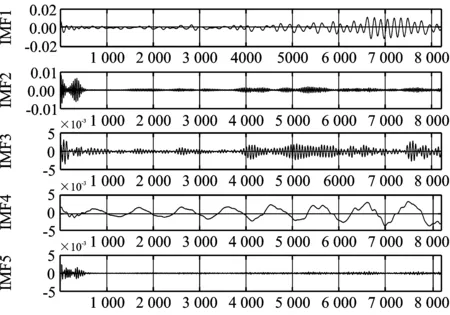
(a)
由图6可以看出,经VMD分解后的各模态分量均没有出现模态混叠现象,且都集中在了各自中心频率的附近。同时,经分解后的IMF中至少存在一个主分量,这些主分量的幅值高于其他分量,成为了轨枕振动信号的主要能量部分,反映了轨道板振动信号的重要特征。
本文通过研究MPE算法理论,设置合适的算法参数,计算这些经VMD分解后的模态分量,从而构建特征向量。其中,嵌入维数m=3,时间延迟d=1,多尺度因子τ=20,部分结果如表1所示。
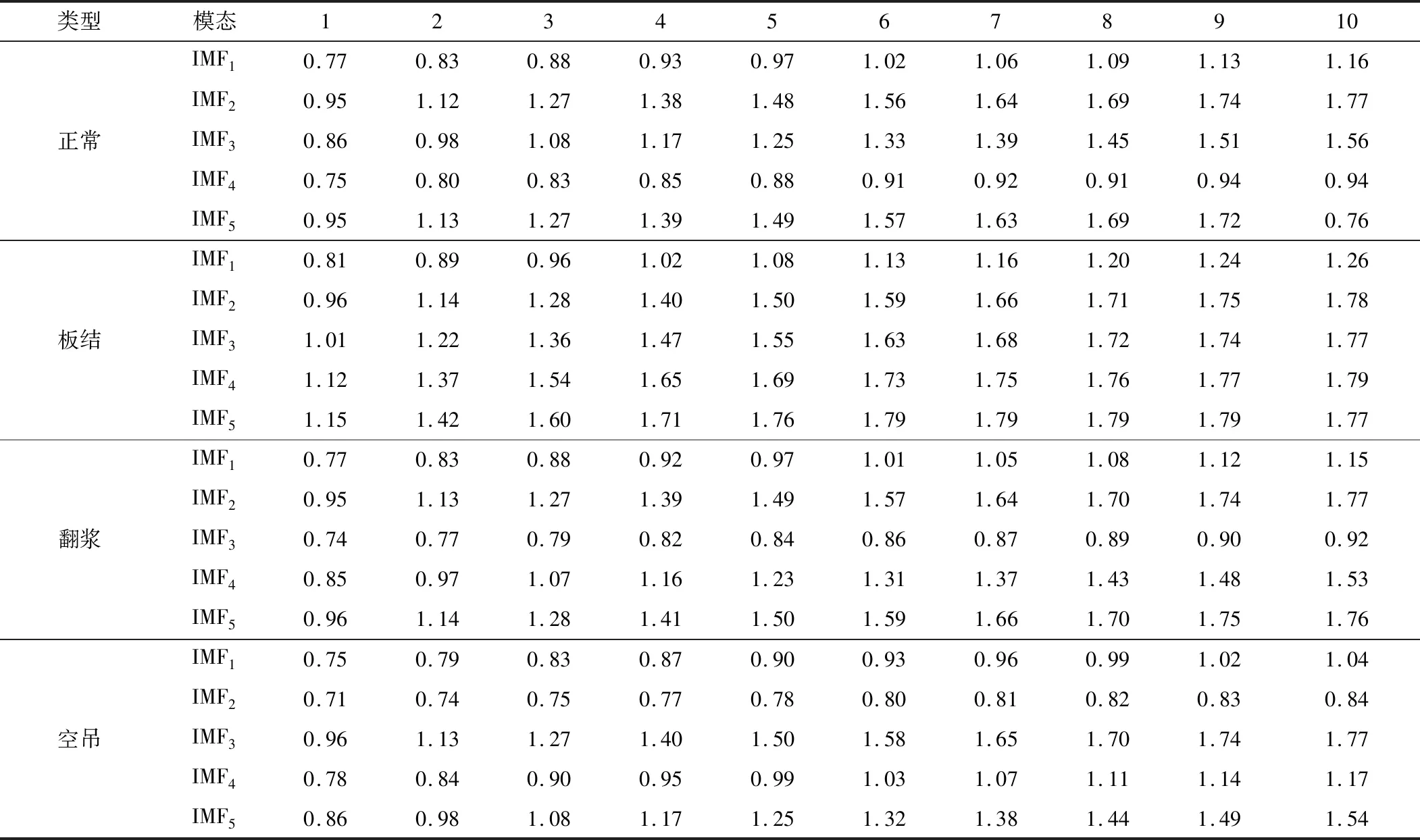
表1 特征向量表Table 1. Feature vectors
3.3 病害识别与结果分析
3.3.1 BP神经网络的建立
(1)输入层和输出层层数的选择取决于实际情况,由于本文在对轨枕信号进行特征提取时,MPE算法的维数是20,即特征向量维数为20,而输入层层数应与特征向量的维数相等,因此输入层的层数为20。同时,输出层层数必须根据模型识别的种类来选择。本文轨道结构服役状态有4种,分别是正常、道床板结、道床翻浆和轨枕空吊,所以输出层层数应为4,即为四维向量;
(2)在BP神经网络中,隐含层层数的选择也十分的重要。一般认为增加隐含层的数量可以降低网络训练误差,从而提高训练的准确度。隐含层数量的增加会使得网络变得复杂,导致训练时间变长,可能会出现过拟合的现象。但是如果隐含层数量太少,网络将无法建立复杂的判断界限,不能训练出合适的网络,导致识别失败,并且容错性差。
关于BP神经网络隐含层层数的确定,有经验计算式[20-21]
(7)
0.02u (8) 式中,u为输入层层数;z为隐含层层数;v为输出层层数;a为1~10的调节常数。 由于本文的输入层层数u为20,输出层层数v为4,根据式(8)计算得出,隐含层层数z的取值范围为1~80,再经由式(7)计算得出,随着a的取值不同,z取值范围为6~15,故本文取隐含层层数z为15。 3.3.2 BP神经网络仿真验证 将经VMD-MPE提取后的特征向量输入BP神经网络模型中,选择180组样本作为训练样本,60组样本作为确认样本。每训练一次都会利用确认样本来检验网络对确认样本的拟合能力。本文以60组样本作为测试样本,设最大训练的步数为1 000步,训练目标的最小误差为0.001,学习速率为0.01。训练结果如图7和图8所示。 图7 误差变化图Figure 7. Diagram of error change 图8 回归分析图Figure 8. Diagram of regression analysis 由图7可以看出,BP网络训练到第5代的时候BP训练结果是最理想的。同时,训练样本、确认样本以及测试样本的误差曲线呈现较好的相关性,曲线缓慢下降,最终达到一个合适的目标误差。由图8可以看出,神经网络拟合度水平较高,训练拟合度、测试拟合度和验证拟合度均达到95%以上,总体准确率高达97.3%,说明BP神经网络能准确诊断故障。 为进一步验证本文所提VMD-MPE与BP神经网络结合方法的有效性,将病害诊断结果与其他方法进行对比。将EMD-MPE方法与BP神经网络相结合,所得病害诊断结果如表2所示。 表2 不同诊断方法结果对比Table 2. Comparison of different diagnostic methods results 由表2可知,传统的EMD分解病害诊断识别率比本文VMD方法低,且由上文信号仿真实验可知,EMD分解振动信号时会出现模态混叠的现象,不能有效提取病害特征,对识别结果有一定的影响。因此,本文采用VMD-MPE与BP神经网络结合的方法对轨道病害进行识别诊断。该方法具有更高的识别率,可有效进行轨道病害诊断。 本文针对轨道病害振动信号,提出VMD预处理MPE的故障特征提取方法。本文建立基于BP神经网络的轨道病害诊断模型,对输入BP网络的数据进行训练、拟合、验证,以实现对轨道病害状态的识别及诊断,并得到以下结论:(1)针对非线性、非稳态振动信号,提出基于VMD方法对轨枕振动信号进行分解。相比于EMD方法,VMD可以有效抑制噪声的干扰,分离出不同频带的模态分量,并且没有出现模态混叠现象,对于病害信息的提取更加全面;(2)利用MPE算法对轨道病害进行特征提取,计算较为简单,采用时间较短,并且MPE算法能够较好地检测故障信号,具有良好的鲁棒性,可以最大程度提取故障信号的有效信息,提高了算法的准确性;(3)利用VMD-MPE实现轨道病害特征提取,并利用BP神经网络对病害进行识别判断,准确率达到97%以上。与EMD-MPE和BP神经网络结合的方法进行对比的结果表明,本文所提方法准确率高于EMD-MPE方法,说明该方法能有效对轨道的病害进行识别,为轨道等非线性非稳态复杂系统的故障诊断提供了一种可行的解决方案。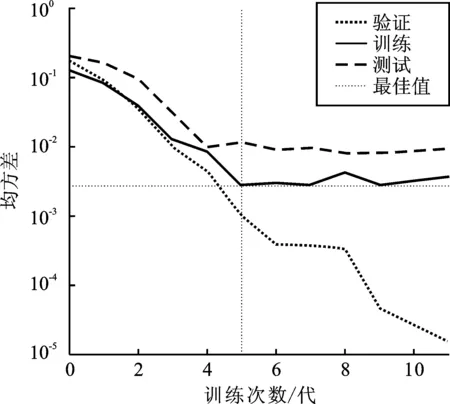


4 结束语

