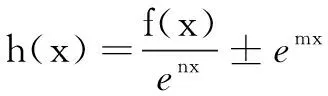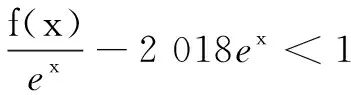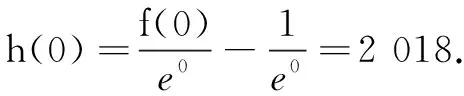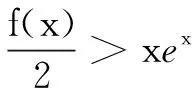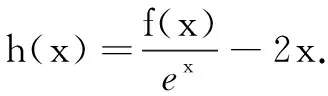例谈求导法则在抽象函数问题中的应用
陈惟前
(江苏省扬州市新华中学,225009)
函数是高中数学的重要内容,而抽象函数则是函数中的一个特殊部分、特殊的分支.由于抽象函数没有具体的解析表达式作为载体,理解和研究起来比较困难.此类题目难度大、灵活性强,因此倍受命题者的青睐.本文举例说明函数的四则运算求导法则在抽象函数导数问题中的解题策略,供大家参考.
一、构造可导和、差函数
一般地,若条件含有f′(x)±g′(x)的结构,根据导数的和差求导法则逆向思维,可构造函数F(x)=f(x)±g(x)解题.
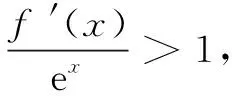
(A)f(2)-f(1)>e2
(B)f(2)-f(1) (C)f(2)-f(1)>e2-e (D)f(2)-f(1) 解依题意,当x>0时,恒有f′(x)-ex>0.构造函数F(x)=f(x)-ex,则F′(x)>0,F(x)在(0,+∞)单调增.于是F(2)>F(1),即f(2)-e2>f(1)-e,即f(2)-f(1)>e2-e,故选C. 变式(2015年福建高考题)若定义在R上的函数f(x)满足f(0)=-1,其导函数f′(x)满足f′(x)>k>1,则下列结论中一定错误的是( ) 一般地,若在题设的已知条件中含有f′(x)g(x)+f(x)g′(x)的结构,根据函数积的求导法则逆向思维,可构造函数h(x)=f(x)g(x)解题. 例2已知f′(x)是函数f(x)的导数,且满足f′(x)+f(x)>0对x∈[0,1]恒成立,A,B是锐角三角形ABC的两个内角,则下列不等式一定成立的是( ) 分析f′(x)+f(x)>0可视为两函数积的导数f′(x)g(x)+f(x)g′(x)>0,且g′(x)=g(x).而原函数与其导数相同的特殊函数可为g(x)=ex,因此构造函数h(x)=exf(x)可使问题获解. 变式已知函数f(x)的定义域为(0,+∞),且满足不等式f(x)+xf′(x)>0,则不等式(x-1)f(x2-1) (A)(-∞,2) (B)(1,+∞) (C)(-1,2) (D)(1,2) 解设函数h(x)=xf(x),其中x>0.则h′(x)=f(x)+xf′(x)>0,h(x)在(0,+∞)单调增. 评注本题由不等式条件构造函数h(x)=xf(x) 还是容易想到的,难点是对目标函数运用同构变形回归到h(x) 在不同两点的函数值大小比较,结合函数的单调性、定义域列不等式组求解. 例3设f′(x)是定义域为R的函数f(x)的导函数,且满足f′(x)>f(x),则不等式ex+1f(x)>f(2x+1)的解集为( ) (A)(-1,+∞) (B)(-∞,-1) 分析由f′(x)>f(x),得f′(x)-f(x)>0.两边同乘以ex,得[f′(x)-f(x)]ex>0. 变式定义在{x|x≠0}上的函数f(x)满足f(x)-f(-x)=0,f(x)的导函数为f′(x),且f(1)=0,不等式xf′(x)<2f(x)对任意x>0恒成立,则不等式f(x)>0的解集为( ) (A)(-∞,-1)∪(0,1) (B)(-∞,-1)∪(1,+∞) (C)(-1,0)∪(1,+∞) (D)(-1,0)∪(0,1) 又f(x)为偶函数,故所求解集为(-1,0)∪(0,1).选D. (A)(0,+∞) (B)(-∞,0) (C)(0,2 018) (D)(-2 018,0) (A)(-∞,1) (B)(1,+∞) (C)(-∞,2) (D)(2,+∞) 总之,解答上述抽象函数问题离不开构造函数,而函数的构造遵循函数求导法则,实际上就是函数求导法则的逆用,更能考查学生对求导运算的全方位把握,更能体现出数学思维的双向变通[1].所以,在求解抽象函数问题时,一方面要重视导数运算法则的逆用及常见导数的原函数,另一方面也离不开函数性质的运用,特别是函数单调性的应用.
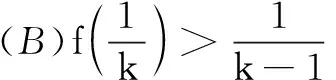
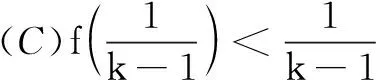
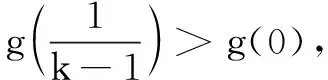
二、构造可导积函数

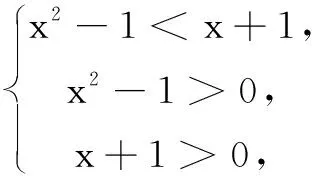
三、构造可导商函数
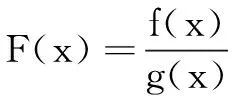
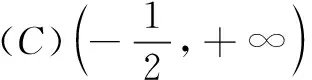
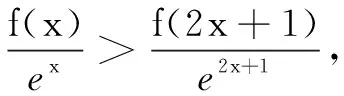
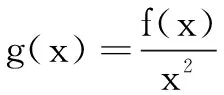
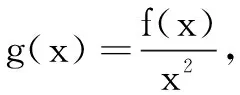
四、构造可导组合型函数