一道高三适应性检测试题的解法探究
晏 鸿
(新疆教育科学研究院,830000)
一、试题呈现

(1)求椭圆C的方程;
(2)过点A(-4,0)的直线l与椭圆C相交于P,Q两点,点P在A,Q之间,点P关于x轴的对称点为R,QR交x轴于点B,求∆PQB面积的最小值.
二、解法探究
(1)思路1常规思路,联立求解
由相切时Δ=0可得a,b之间的关系,再结合c=1,求出a,b的值.
解法1联立直线与椭圆方程,可得(4b2+a2)y2-16b2y+16b2-a2b2=0.由Δ=0,得256b2-4(4b2+a2)(16b2-a2b2)=0,整理可得a2+4b2=16.

思路2巧设方程,适度优化
选用椭圆的一般方程,可使计算适度简化.

思路3妙用参数方程,简化计算
有时巧用椭圆的参数方程,会有意想不到的效果,使复杂计算大大简化.
解法3设P(acosθ,bsinθ)为椭圆上任意一点,则点P到直线x-2y+4=0的距离
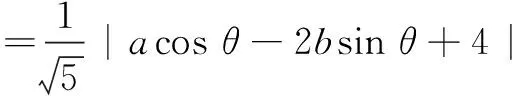
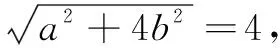
下同解法1.(过程略)
思路4仿射变换,高观点求解
直接计算较复杂,可用高观点下的仿射原理,将椭圆仿射为圆,来化简复杂的计算问题.

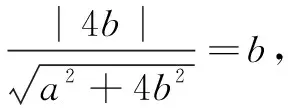
(2)思路1常规策略,设而不求
由直线l过定点A,且P和R关于x轴对称,可考虑使用设而不求法结合韦达定理表示出点B的坐标,再利用S∆BPQ=S∆ABQ-S∆ABP,求∆BPQ面积的最小值.


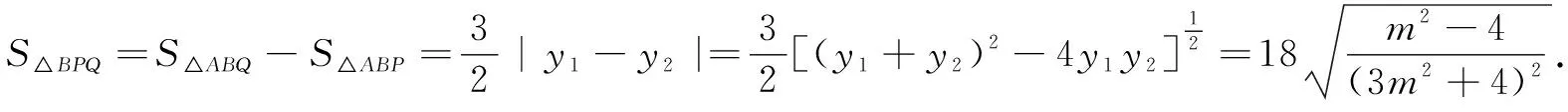
思路2利用坐标特点,齐次化显神威


设直线QB方程为m(x+4)+ny=1,由P,Q不重合,得n≠0.
椭圆方程可变形为3(x+4-4)2+4y2-12=0,即3(x+4)2+4y2-24(x+4)+36=0.齐次化可得3(x+4)2+4y2-24(x+4)[m(x+4)+ny]+36[m(x+4)+ny]2=0,整理得(36m2-24m+3)(x+4)2+(72mn-24n)(x+4)y+(36n2+4)y2=0.

于是直线QB的方程为x+3ny+1=0.令y=0,可得点B(-1,0).

S∆BPQ=S∆ABQ-S∆ABP

三、亮点赏析

——从广州一模的一道选择题谈起

