例谈恒成立问题中参数取值范围的求解策略

袁小强

(江苏省兴化市楚水实验学校,225700)

求函数不等式恒成立问题中参数的取值范围一直是高考及各种模考中常见问题，它覆盖了各种数学思想方法的考查.笔者通过一道例题解法的归纳和梳理，总结出解决该类问题的常用几种策略.不当之处，敬请批评指正.

题目已知定义在R上的奇函数f(x)在(-∞,0]单调增,且对任意x∈(0,1],不等式f(aex+2x)+f(xlnx-x2)≥0恒成立,求实数a的取值范围.

解由f(aex+2x)+f(xlnx-x2)≥0,得f(aex+2x)≥-f(xlnx-x2),结合f(x)是奇函数,得f(aex+2x)≥f(x2-xlnx).

由f(x)是定义在R上的奇函数,且在(-∞,0]单调增,得f(x)在R上单调增.故aex+2x≥x2-xlnx对任意x∈(0,1]恒成立.

策略1参变分离法

解法1参变分离法

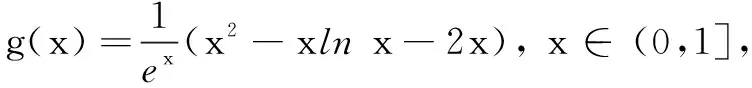
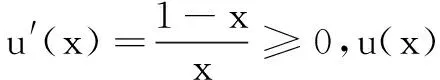
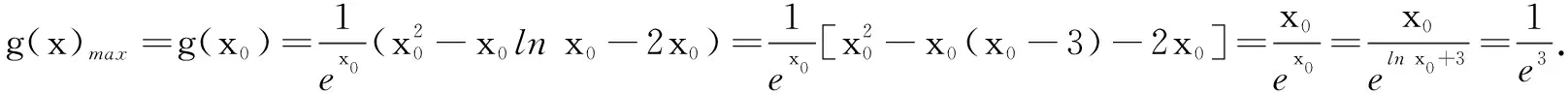
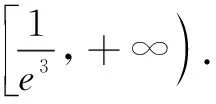
评注参变分离法是处理函数不等式恒成立时求参数取值范围的常见策略.其优点是可将问题转化为定函数的最值求解,缺点是函数最值的求解往往比较麻烦,有时需要运用隐零点进行代换,且使用时需注意参数a的系数,有时需要对a的系数分类讨论,解题思路虽然简单清晰,但运算量较大.

策略2同构法与函数分析法综合

解法2函数最值法

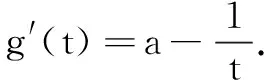
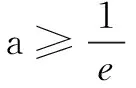
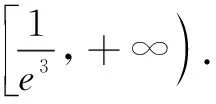
解法3参变分离法

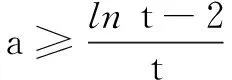
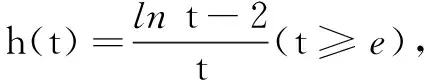
评注解法3在同构的基础上再分离参数，优化运算,简化了解题过程.

解法4切线法

由at≥lnt-2对任意t∈[e,+∞)恒成立,构造函数g(x)=lnx-2与y=ax,其中t∈[e,+∞).

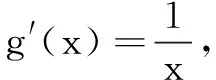
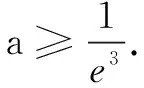
评注数形结合法也是研究恒成立问题的常见处理策略.切线策略需要把不等式转化为常见函数与一次函数,研究切线这种临界状态,利用数形结合简化复杂的运算,可达到优化解题的目的.

解法5放缩法

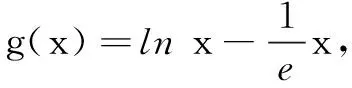
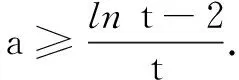
评注课本上有ex≥x+1, lnx≤x-1等常见结论,熟悉和运用课本上习题的一些二级结论,对学生的能力有较高要求,在理解中运用,如果放缩有度、有张有弛,同样可以优化解题.