例说一类双变量最值问题的求解策略

刘 艳

(四川省名山中学,625100)

例题呈现已知a∈R,b>0,若a,b满足ea-1-2-ln 2b=0,则a-b的最大值为______.

策略1配凑消元

解题思路首先由已知双变量的等式关系,将两个变量分离得到ea-1=2+ln 2b,利用左边配凑出含有所求式的代数式结构ea-b=ea-1e1-b=(2+ln 2b)e1-b,由此达到消元的目的,构造一元函数f(b)=(2+ln 2b)e1-b(b>0),利用导数研究其单调性,求出目标函数的最值.

解法1由条件分离变量,可得ea-1=2+ln 2b.于是ea-b=ea-1e1-b=(2+ln 2b)e1-b.

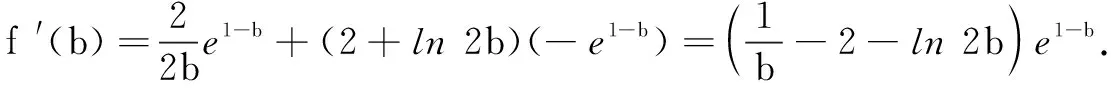
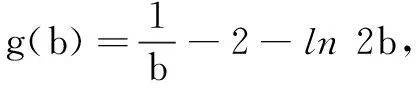
策略2换元法

解法2由ea-1-2-ln 2b=0,得ea-1=2+ln 2b.

策略3切线转化法

解题思路考虑到在已知双变量等式关系中,a与b的地位相同,故可以将a(或者b)看成自变量,另一个看成因变量.例如，本题可将b看成自变量,a看成因变量,则可将已知等式转化为a=1+ln(2+ln 2b),于是点(b,a)在相应曲线a=1+ln(2+ln 2b)上.再令所求式为z=a-b,则可视a=b+z是一条斜率为1的直线.将直线进行平移,当且仅当直线与曲线相切时z取得最值,求出切点坐标,可得出最值.

解法3由条件ea-1-2-ln 2b=0,可得a=1+ln(2+ln 2b).

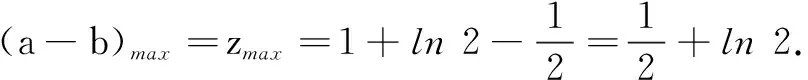
策略4拉格朗日乘数法

解题思路利用拉格朗日乘数法,直接构造拉格朗日函数L(a,b,λ)=a-b+λ(ea-1-2-ln 2b),其中a,b,λ都是变量.然后分别对a,b,λ求导(其他量均为常量),并令求导后的式子为0,解方程组,得到对应的a,b,λ,可求出最值.

解法4构造拉格朗日函数L(a,b,λ)=a-b+λ(ea-1-2-ln 2b),对L求偏导数并令其都为0,可得

综上可见,针对这类双变量最值问题,我们可以利用配凑消元法或换元法将双变量转化为一元变量最值问题;如果所求式为线性结构,也可以选择切线转化法,借助线性规划的方法求得最值;而拉格朗日乘数法来源于高等数学,理论上是解决多元变量的通法,虽超出高中数学范围,但可供解题时参考.