巧用“指数积求导法”探求一类函数最值

沈玉良

(浙江省湖州市滨湖高级中学,313000)

一般来讲,有些含有指数函数ex的函数是求不出极值点的.如f(x)=ex+x2,通过求导得到f′(x)=ex+2x,此时无法求出f′(x)零点的准确值,也就是求不出函数f(x)的极值点,从而求不出此类函数的极值与最值.

笔者通过研究发现,有一类特殊的含有指数函数ex(或e-x)的函数可轻松求出极值点,其形式如下:

(1)若f(x)=exg(x),则f′(x)=ex[g′(x)+g(x)];

(2)若f(x)=e-xg(x),则f′(x)=e-x[g′(x)-g(x)].

对于以上形式的函数,其极值点与ex(或e-x)无关,只与g′(x)±g(x)有关,若g(x)的形式是多项式函数,我们就可以通过函数乘积的求导法轻松地求出函数f(x)的极值点.笔者称这种做法为“指数积求导法”.下面举例说明其应用.

例1证明:当x≥0时,ex≥ex+(x-1)2.

分析看到以上证明题,给人的直觉是先移项整理成ex-ex-(x-1)2≥0,再令f(x)=ex-ex-(x-1)2,求出它在x≥0时的最小值刚好为0,则原题可获得证明.以上思路好像很自然简单,然而实际操作就发现，确定f(x)的单调性与极小值存在困难,具体过程这里就不赘述了.下面改用“指数积求导法”来证明.

证明当x≥0时,要证ex≥ex+(x-1)2,即证e-x[ex+(x-1)2]≤1.

设f(x)=e-x[ex+(x-1)2],g(x)=ex+(x-1)2,则f(x)=e-xg(x),且f′(x)=e-x[g′(x)-g(x)]=e-x[e+2(x-1)-ex-(x-1)2]=e-x(x-1)(3-e-x).由此易见f(x)在[0,3-e), (1,+∞)单调减,在(3-e, 1)单调增.

又计算得到f(0)=1,f(1)=1,故f(x)在[0,+∞)的最大值为1.于是f(x)≤1,即原不等式得证.

评注由本题可见,当函数解析式中出现单个的指数函数的时候,利用传统方法求最值就显得困难重重,而在解题方法和技巧上能够充分认识和掌握“指数积求导法”,可以起到化繁为简的效果.

例2(2018年全国高考题改编)已知函数f(x)=ex-ax2.若a=1,试证明当x≥0时,f(x)≥1恒成立.

分析本题的传统做法涉及到二阶求导、隐零点问题,解法比较繁琐.故仿照以上“指数积求导法”求解,可使问题轻松得证.

解当x≥0时,不等式ex-x2≥1等价于ex≥x2+1,亦即等价于e-x(x2+1)≤1.

令g(x)=e-x(x2+1),则g′(x)=e-x(2x-x2-1)≤0,g(x)在 [0,+∞)单调减,可得g(x)≤g(0)=1.故原不等式成立.

例3(2020年全国高考题)已知函数f(x)=ex+ax2-x.

(1)当a=1时,讨论f(x)的单调性;

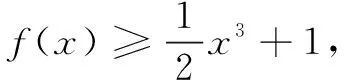
解(1)略.

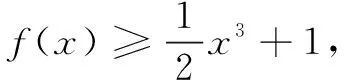
评注在最值问题、恒成立问题中,导数的应用非常广泛,在常规求导中可以留意指数函数是否有一个“黄金搭档”,“指数积求导法”对解决这一类高考热门题往往可以起到事半功倍的效果.“指数积求导法”往往与逆向思维、整体思想串联在一起,有时也需要一定的洞察力(如例2,例3),有助于考查考生的综合分析能力与应变能力.通过对以上问题的探究,可以让研究性学习深入课堂、深入人心,使学生切身体会到其实高考题就在身边.