支架式教学法在复习课中的应用——以“利用导数研究函数的单调性”复习课为例

南爱玲

(江苏省苏州市南京航空航天大学苏州附属中学，215021)

《普通高中数学课程标准》(2017年版)(以下简称《标准》)强调,“高中数学教学以发展学生数学学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质．”

建构主义学习理论下的支架式教学模式是指一步一步地为学生的学习提供适当的、小步调的线索或提示(支架),让学生通过这些支架一步一步地攀升,逐渐发现和解决学习中的问题,掌握所要学习的知识,提高问题解决能力,成长为一个独立的学习者．其核心是将复杂的学习任务加以分解,以便将学习者的理解逐步引向深入．本文以“利用导数研究函数的单调性”复习课为例，探讨以支架式教学理论为指导,如何在学生的最近发展区设计问题,层层递进,培养学生解决问题的能力,发展数学核心素养．

一、课堂实录

1.回归课本，脚踏实地

师:导数是研究函数单调性的一个重要工具,本节课我们就来复习导数在研究函数单调性中的应用．

例1(选修1-1第89页习题4改编)求函数y=x-lnx的单调区间．

师:请同学们考虑这个问题怎么解决?

生:研究函数的性质,先看定义域,这个函数定义域是(0,+∞)．求导,令导数等于零,求出零点,再列表得出导数符号,进而确定单调区间．(解题过程略)

师:说得很好!函数问题首先考虑定义域,然后根据导数符号与函数单调性的关系解决问题．

2.循序渐进，层层深入

师:这个题目是一个具体的函数,如果含有参数a,对函数的单调性会有什么影响呢?

变式1研究函数y=x-alnx,a∈R的单调性．

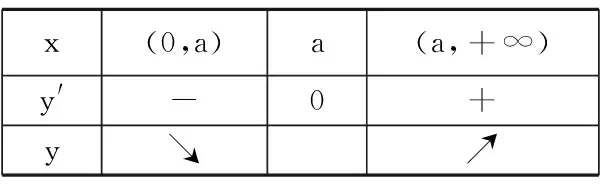
x(0,a)a(a,+∞) y'-0+ y↘↗

故增区间是(a,+∞),减区间是(0,a)．

师:考虑很全面,分类讨论的依据也很清楚,根据a的范围讨论了不同情况下函数的单调性．如果把a放到x前面,会有什么变化呢?

变式2研究函数y=ax-lnx,a∈R的单调性．

师:你为什么要分a=0和a≠0讨论呢?

生:因为a在一次项系数上．

师:你怎么看出来它是一次项系数的?

师:继续说下去．

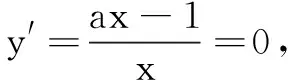
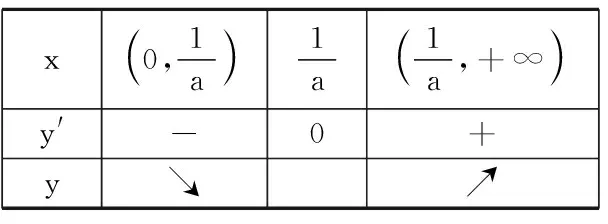
x0,1a 1a1a,+∞ y'-0+ y↘↗

师：这位同学虽然一开始碰到一点小困难,但是后面克服了困难，顺利解决了这个问题．解完这个题,你的感受是什么?

生:在求导数后要及时通分,将研究导数的符号转化为研究导函数中分子的符号．

师:总结得很好!接下来看变式3．

变式3研究函数y=ax2-lnx,a∈R的单调性．

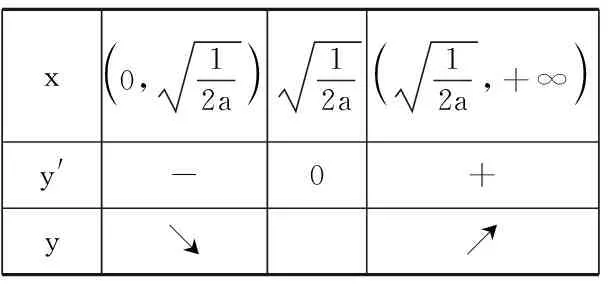
x0,12a 12a12a,+∞ y'-0+ y↘↗

师:这位同学思路清晰,表达完整规范,能说说这一题跟变式2有何联系与区别吗?

党的十九大以来，省委省政府对加快构建现代综合交通运输体系给予了前所未有的关心重视和大力支持。省委书记娄勤俭指出，高质量发展是一个系统化工程，其中最核心的是创新驱动，最主要的是建设现代化经济体系，最迫切的是建设综合交通运输体系。

生:这两题共同之处是分类讨论的标准差不多,考虑导数是否有零点,零点是否在定义域内,分类时a的范围是一样的,不同之处是通分后分子一个是一次函数,一个是二次函数,在画示意图时有所区别．

3.融会贯通，提炼升华

师:总结得很到位．下面这个问题请同学们思考一下．

变式4研究函数f(x)=lnx+ax2-(2a+1)x,a∈R的单调性．

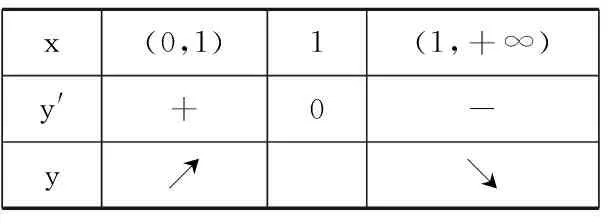
x(0,1)1(1,+∞) y'+0-y↗↘

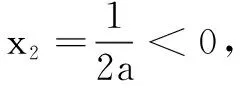
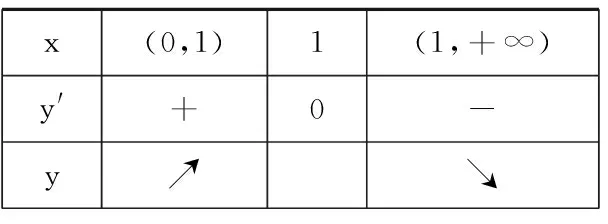
x(0,1)1(1,+∞) y'+0- y↗↘

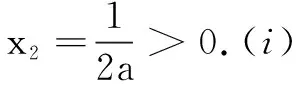
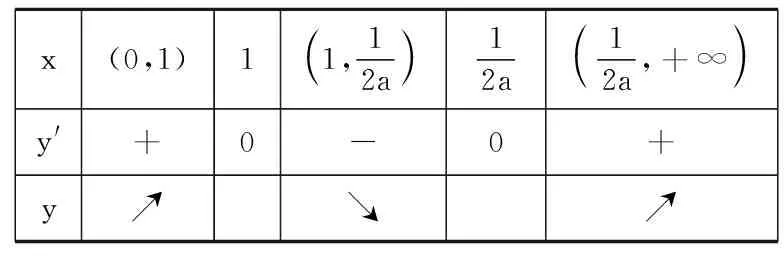
x(0,1)11,12a 12a 12a,+∞ y'+0-0+ y↗↘↗

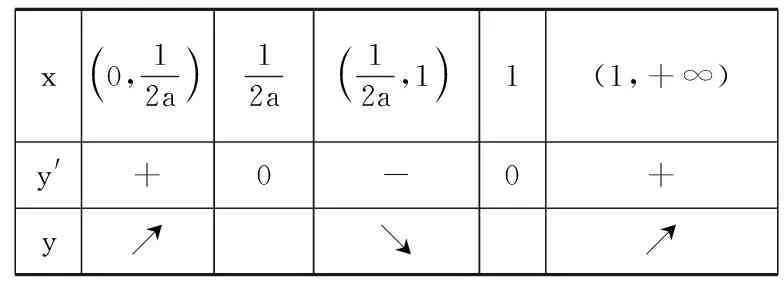
x0,12a 12a12a,1 1(1,+∞) y'+0-0+ y↗↘↗

师:思路清晰,但是解题过程中存在一些问题,有没有同学发现?

师:还有吗?

师:这也是很多同学在做题时经常会忽略的地方,逻辑顺序错误,以后解题时要注意．接下来请同学们总结一下，如何利用导数研究含参数函数的单调性?

生1:首先考虑定义域,求出导数的零点,判定零点是否在定义域内,如果两个零点都在定义域内，要讨论零点的大小关系,不能忘了相等的情况．

生2:导数也可能没有零点,说明其符号是恒正或者恒负的．

生3:在判断导数符号的时候要尽量画出图象,根据图象看符号不容易错．

生4:如果导数最高项系数含参,要讨论系数的符号,尤其要先讨论系数等于零的情况．

师:同学们对这部分知识点总结得非常好,想想还渗透哪些数学思想方法呢?

生:分类讨论和数形结合．

师:还有吗?

生:还有转化与化归,求导之后通分的过程实际上就是将导数的符号转化为一次函数或者二次函数的符号．

师:归纳得很全面,知识点和思想方法的掌握也很到位．下面做一道课堂练习,测试一下自己对这类问题掌握的程度．

4.趁热打铁，及时反馈

课堂练习已知函数f(x)=lnx+x-ax2,a∈R.

(1) 若f(x)在x=1处取得极值, 求a的值;

(2) 设g(x)=f(x)+(a-3)x,试讨论函数g(x)的单调性．

(投影展示学生的作业并点评)

二、教学反思

1.注重知识生成，领悟理解

课堂是知识生成、生长、发展的主阵地,抓住课堂、提高效率是值得每一位教师思考的问题．导数是研究函数单调性的一个重要工具,而利用导数研究含参数函数的单调性是重点也是难点．本节课通过具体问题将含参数的难点分解,逐个剖析,从一次函数到二次函数,从导数零点是否存在,到有两个零点,层层铺垫,为学生搭建学习支架,符合学生的认知规律,促进学生对这一题型的充分理解．在变式2的教学过程中,当学生没有理解分类的标准导致做不下去时,教师并没有急着告诉学生应该怎么做,而是通过两个问题“你为什么要分a=0和a≠0讨论呢?”“你怎么看出来它是一次项系数的?”引导学生自己发现问题并及时采取通分的措施将问题继续解决．

2.注重思想方法，激活思维

莱布尼兹指出,数学的本质不在于它的对象而在于它的思想、方法．知识是载体,思想是根本,在学习过程中让学生掌握基础知识的同时感悟数学思想方法．利用导数研究函数的单调性,求出导数后通分这一步骤,体现转化与化归的思想方法,将导数的符号转化为基本初等函数(一次函数或二次函数)的符号问题．本节课自始至终渗透着分类讨论的思想方法,在解题的过程中帮助学生理解分类讨论的标准、分类讨论的步骤以及注意点,做到不重不漏,注重培养学生严谨的思维方式．思想方法也是核心素养的一种体现,掌握思想方法就是从宏观层面上把握住知识的学习和理解,促进知识的内化．

3.培养学生能力，提升素养

数学核心素养以数学基础知识和基本技能为载体,培养学生数学综合能力,引导学生形成数学思维与数学态度．数学核心素养的培养不是凭空想象的,而是扎根于课堂教学这块土壤.在教学实践中学生积累活动和思维的经验,数学核心素养在基本活动经验的积累中不断提升．数学解题的过程就是一个学生活动的过程,包括学生的思维活动,在解题的过程中培养学生能力,激活学生思维,为提升数学核心素养提供平台．在教学过程中,让学生充分参与学习活动,经历反思、领悟、深化,将数学理性思维潜移默化为学生内在思维品质,提升学生的数学核心素养．