以题为媒 发展思维
杨兴刚
(江苏省淮安市北京师范大学淮安学校,223001)
美国数学家哈尔莫斯(P.P.Halmos)说过:“数学的真正组成部分应该是问题和解,解题才是数学的心脏”.数学学习离不开解题,为了促进学生对数学知识的深度理解、对解题方法的灵活应用、对数学思想的深刻领悟、对解题活动经验的持续积累,适度地解题是数学学习必不可少的环节.应基于数学素养选择具有启发性的好题,注重通性通法训练,探索解题方法创新,激活学生数学思维,反思总结解题经验,通过解题提升数学思维能力与解决问题的能力,引导学生进行深度学习,起到触类旁通的效果.本文以选题、解题、反思谈谈具体做法.
一、素养选题,注重思维
数学是培养学生思维能力的重要学科,数学试题是数学思维的重要载体,数学素养是每个学生都应该具有的基本素养.数学习题课教学应着眼于数学核心素养选题、注重学生数学思维能力培养.这样,不仅可以有效考查学生数学知识、基本技能方法的掌握情况,而且更能体现学生思考问题的角度和深度,知识的迁移和创新应用能力,科学的思维习惯和态度.学生在真实的情境中整合试题的复合要素,展现数学的思维过程,探究创新的学习意识,构建适当的数学模型,形成创新性的思维方式和批判质疑的思维习惯.
1.选取教材习题,培养发散思维
案例1(苏教版选修2-2,第56页第8题)如图1,已知海岛A到海岸公路BC的距离AB为50 km,B,C间的距离为100 km,从A到C,先乘船,船速为25 km/h,再乘汽车,车速为50 km/h,登陆点选在何处,所用时间最少?
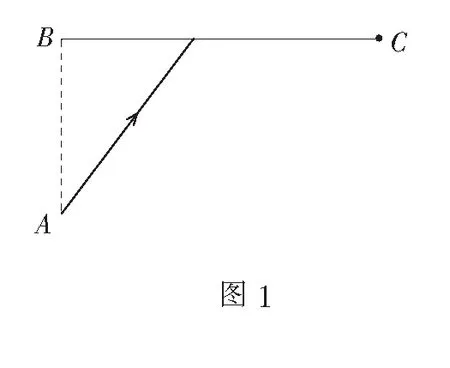
选题意图本题对接2008年江苏高考数学试卷第17题,具有一定的开放性和探究性,基于培养学生的数学抽象、数学运算和数学建模素养选题,注重考查学生分析问题的角度、思考问题的深度、解题方法批判性选择、创新思维意识和构建数学模型的能力.本题一般有以下不同的解法:几何方法等价转换为将军饮马问题、代数方法用登陆点到B点的距离或者航行方向与AB的夹角表示所用时间、学科融合运用最小光程原理解决问题.选用此题可充分激发学生的参与热情、激活学生的思维,让数学素养落地生根.
2.选取典型试题,培养逆向思维
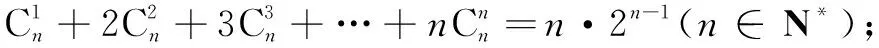
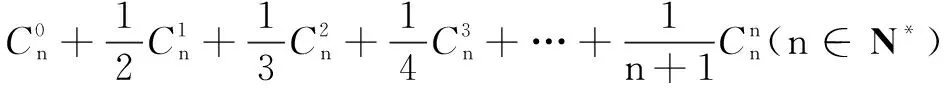
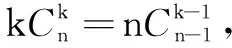
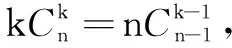
选题意图本题基于培养学生逻辑推理、数学运算素养,试题解法多样,融合数列、组合数公式、函数与导数、数学归纳法等多个知识点,鼓励学生联想知识、串联方法、解决问题,培养学生逆向思维习惯.
3.选取文化试题,提升综合能力
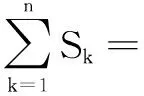
选题意图本题基于培养学生的阅读能力、理解能力、数学直觉和创造能力,提升学生的数学抽象、数学建模和数学运算素养,将数列知识融入中国传统折纸文化,引导学生通过阅读提取数学信息、通过归纳猜想构建数学模型、通过数列求和知识解决问题.本题充分发挥数学文化,试题不仅承载数学知识、思想和方法,而且能使学生充分认识到数学文化的价值所在.不仅可以让学生了解数学的历史、现状和未来,体悟数学的思想方法,而且可以开阔学生的视野,感受数学的应用价值,还能提高学生的数学素养、文化素养和理性精神.
二、 尝试解题,渗透思想
尝试解题是对所选试题的思维暴露和交流表达过程,是学生思维碰撞、批判质疑的思考过程,应有效发挥数学素养的宏观指导性、数学思想方法的微观引领性和数学知识的灵活应用性.学生在解题的过程中收获的不应该局限于试题的答案是什么,试题的解答过程是怎样的,而应该充分展现学生思考问题的角度,批判质疑的分析、修正错误的过程,挖掘出试题蕴含的思想方法和考查的数学素养,让学生站在更高的角度理解试题的价值.
1.基于直观想象,渗透数形结合
案例4(2021年新高考Ⅰ卷第11题)已知点P在圆(x-5)2+(y-5)2=16上,点A(4,0),B(0,2),则( )
(A)点P到直线AB的距离小于10
(B)点P到直线AB的距离大于2
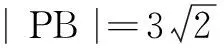
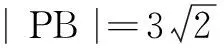
评析图形不仅是几何题目的对象,而且对任何一开始跟几何没什么关系的题目,图形也是一个重要的帮手[2].本题的入手点是将题目所给代数形式转化为几何图形,根据直观图形考查直线和圆的位置关系.选项A,B的判断依据是将动态问题(点P在圆上运动)转化为静态问题(圆心(5,5)到直线AB的距离);选项C,D基于极端原理将∠PBA的大小问题转化为过点P的切线问题,进而利用切点、圆心、点P构成的直角三角形解决问题.
2.基于数学抽象,渗透归纳推理
案例5若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)是集合A的同一种分拆.若集合A有三个元素,则集合A的不同分拆数是______.
评析本题涉及集合的新定义问题.解决问题的首要任务是审题,基于数学抽象,将集合A中的元素特殊化,挖掘出题目蕴藏的关键信息,然后采用枚举法一一列举出所有的可能情况得到问题的解答;引导学生深入思考,改变集合A中元素的个数、考虑集合A的三个集合的分拆形式等等,引导学生在逻辑推理的过程中发现问题蕴藏的规律性和一般性,培养学生由特殊到一般思考问题的方法,并尝试用排列组合、构造模型的策略深入解答问题,充分发挥试题提升学生思维能力的最大功效.
3.基于数学建模,渗透模型思想
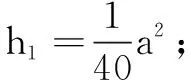
(1)求桥AB的长度;

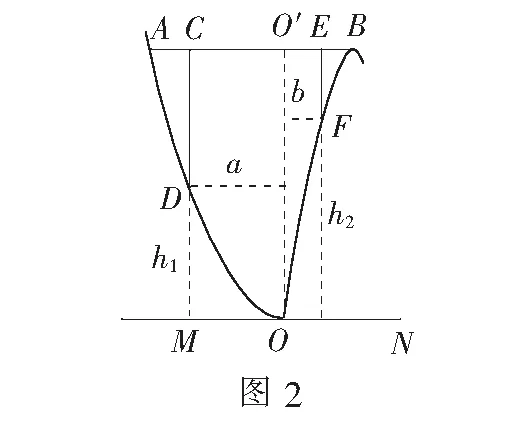
评析数学建模是架设在数学与应用之间的一座桥梁.本题基于数学建模,通过学生的阅读理解与文字信息提取,构建几何直观,用数学的眼光观察实际问题,构建数学模型.解答本题的关键是通过平面几何知识建立平面直角坐标系,用解析的方法建立函数模型、通过导数求解函数的最值,灵活运用数学知识分析和解决实际问题,培养学生的直观想象和数学建模素养.
三、解题反思,形成经验
孔子指出:“学而不思则罔,思而不学则殆”.美国心理学家波斯纳提出的成长公式“经验+反思=成长”同样适用于解题能力的获得与提升[2].解题为学生数学深度学习和深度思考提供了媒介,解后反思是学生对数学知识的理解与感悟,是对解题思维的概括与提升,是对解题经验的积累与优化.
数学知识是数学能力和数学素养形成的根基,数学知识的理解与感悟需要通过解题进一步深化,解题反思是将知识转化为经验、将经验转化为能力、将能力形成数学素养的必备过程.比如通过案例1的解题反思,可以让学生感受学科之间的有效融合,物理为数学提供丰富的学习背景材料,数学又为物理的蓬勃发展提供深刻的理论和精确的运算;还可以让学生体验实际问题可以通过数学抽象表达为数学模型,进而通过引入变量转化为函数问题,借助导数求解问题的最值和优化问题.
解题思维是数学思维的完美展现.解题过程中要及时概括思维的起点、思考的角度、深入的途径,将各种思维模式内化为观察问题、分析问题和解决问题的能力,提升自身的数学素养.比如通过对案例2的解题反思,可以让学生体会逆向思维是解决问题的关键,导数和积分运算是可以互相转化的形式;通过对案例5的解题反思,可以让学生感悟问题的本质是集合A可以划分为A1-A2,A1∩A2,A2-A1互不相交的三部分,集合A中的每一个元素都只属于三部分中的一个,共有33=27种可能,因此问题可以得到进一步推广.
解题经验是学生数学活动经验的重要组成部分,解题经验的积累与优化可以有效提升学生对问题的多元表征能力,比如案例1学生有如下不同的表征方式:
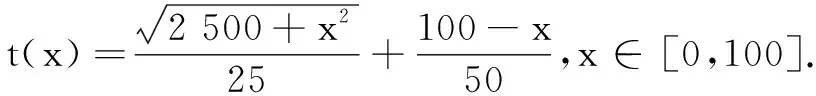
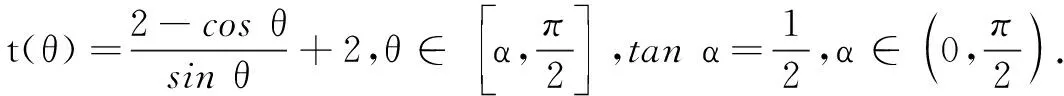
表征3过点C作射线CE,使得∠BCE=30°,过点D作CE的垂线DF交CE于点F,则DC=2DF.所以,质点以50 km/h的速度从点D到点C所用的时间等于以25 km/h的速度从点D到点F所用的时间,因此从点A到点D再到点C所用的时间等于从点A到点D再到点F的时间.
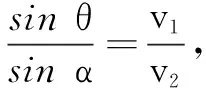
基于数学素养选题,让学生在解题的过程中最大限度地激活数学思维,感悟数学的思想方法,不断积累解题经验、提高解题能力、提升数学素养.所以,解题教学要精心选题,让试题指向数学本质、激发学生深度思考;解题教学要激活学生思维,体现试题考查关键能力、聚焦数学核心素养的功能;解题教学要关注解题反思,让试题有利于学生解题经验获得,有利于学生深度学习.

