基于课本内容的数学阅读理解题编拟

邱钰童 严亚强

(苏州大学数学科学学院,215006)

数学阅读理解题作为考查学生核心素养和关键能力的“新题型”,注重通性通法的提炼,促进学生阅读自学,体现综合性与创新性,必将在新高考的考查中发挥不可替代的作用．由此可见有针对性地编拟与教材配套的数学阅读理解题的工作迫在眉睫．配套习题的使用,可以消除学生对于此类题型的陌生感,在熟悉“阅读理解”模式的同时,引导学生阅读自学,做好“思维的体操”．本文对此进行探讨.

一、阅读理解题的内涵、价值和编拟现状

1.内涵与价值

马云鹏等人指出:“数学阅读理解题是指在阅读一段数学描述之后,按照某一指定要求进行作答、侧重考查分析理解能力的一种题型”[1].阅读理解的过程是建立在分析材料基础上对问题的理解与知识的迁移,一方面考查学生对新知识的理解和应用,又能促进学生数学思维能力的提高[2].经过有效的阅读理解题练习,数学阅读理解题可以发展为一种自适应学习,它们或是渗透某些数学方法,或体现某种数学思想,或提供某些重要结论,对提高学生的自主学习能力、概括迁移能力、逻辑推理和归纳分析能力有着重要的积极作用,所以,深入研究阅读理解具有现代教育意义．

2.编拟现状

编拟数学阅读理解题常用的技巧很多,一般认为，以过程检查的方式编拟、以方法迁移的方式编拟和以定义新运算、新概念的方式编拟是最常用、最有效的三种方法．本研究在此基础上增加以课本习题改编的方式编拟、以数学文化再创造的方式编拟两种方法．另外进行习题设计时,为了有效地帮助学生复习巩固所学的知识与技能,考虑到题目的专题性、模仿性、集中性,还应该有一定的重复性．同时发挥习题的知识、育人与评价功能．

二、数学阅读理解题编拟的常用方式

1.以过程检查的方式编拟

习题1在学习了集合的基本运算后,老师要求同学解决如下问题:设A={x|x2-x-6=0},B={x|2ax+1=0},若A∩B=B,求符合条件的a有多少个?

一个学生给出的解法如下:

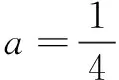
请指出该解法的错误之处,并给出正确解法.

评析本题与人教A版必修一第1章“集合与常用的逻辑用语”配套,主要考查学生对于集合知识点的掌握程度,考查学生的批判性思维．这类改错题常常涉及错误样例的识别与改正．Tennyson Cocchiarella以及Bransford和Schwartz的研究发现,错误样例学习是非常有效的[3].GroBe和Renkl研究结果发现,正、误样例的学习才对迁移成绩有积极的作用[4].编拟这一类阅读理解题，一方面可增加后续正确解法的可能性;另一方面降低错误解法的可能性,提高学习的效果．

2.以方法迁移的方式编拟

习题2互为反函数的指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)的图象关于直线y=x对称;而所有偶函数的图象都关于y轴对称．现在我们定义:如果函数y=f(x)的图象关于y=x对称,即已知函数f(x)的定义域为D,∀x∈D,若y=f(x),x=f(y)也成立,则称函数f(x)为“自反函数”．显然斜率为-1的直线所确定的一次函数都是“自反函数”,它们都为单调递减的函数．请举出一种自反函数,并说出它的基本性质．

评析本题与人教A版必修一第4章“指数函数与对数函数”配套，要求学生考虑函数及其反函数性质的同时,需要抓住反函数的基本性质——∀x∈D,若y=f(x),则x=f(y),筛选一些已经学习过的初等函数．此类题着重考查学生的概括迁移能力和分析归纳能力．数学中“迁移”的核心是类比,通过类比被模仿对象解决问题．TIMSS报告揭示,许多学生不能以类比进行推理,他们看不见数学思想之间的结合与联系,不能用已有的理解去把握新情境．因此,在数学教学中进行方法迁移非常重要,是学生学习的基本过程．

3.以定义新运算、新概念的方式编拟

习题3已知集合A={1,2,3,4,5},集合B={(x，y)|x∈A,y∈A,x，y∈A},则集合B中所含元素的个数为______.

评析本题与人教A版必修一第1章“集合与常用的逻辑用语”配套．定义一个新运算,或定义一个新概念,然后解决一个与之相匹配的数学问题,采用这一方法编制的阅读理解题,是考查学生理解能力的有效方式．但应当强调的是,所要定义的新运算、新概念应当是中学生能够理解的,不能将大学中的高等数学知识作简单下移式处理就来编题．与上题类似的,高考中常常以集合与命题知识为依托,既能考查学生的理解、迁移知识的能力,又能考查学生的探究能力与创新能力．

4.以课本习题改编的方式编拟

习题4函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数．现发现可以将其推广为:函数y=f(x)的图象关于点P(a，b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数.

(1)求函数f(x)=x3-3x图象的对称中心;

(2)类比写出“函数y=f(x)的图象关于y轴成对称图形的充要条件是函数y=f(x)为偶函数”的一个推广结论；

(3)试写出函数y=f(x)的图象与函数y=g(x)的图象关于点P(a，b)成中心对称的充要条件.

评析本题知识源自人教A版第3章“函数的概念与性质”的拓广探索第13题.学生在学习函数的奇偶性时,书中并没有直接展示这一定理,本习题以阅读材料的形式开宗明义,渗透已学奇偶性中有关对称性的一般化结论．第(3)题进一步把一个函数本身的中心对称问题推广到两个函数的对称关系,引导学生进一步积极思考、主动探索,从而得出结论．而此类题更是给学生提高一般化的研究思路与方法，考查学生数学抽象能力同时,引导学生分析问题,解决问题．

5.以数学文化再创造的方式编拟

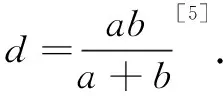
(1)如图2,在斜边上内接正方形(弦上容方),请计算内接正方形的边长y；

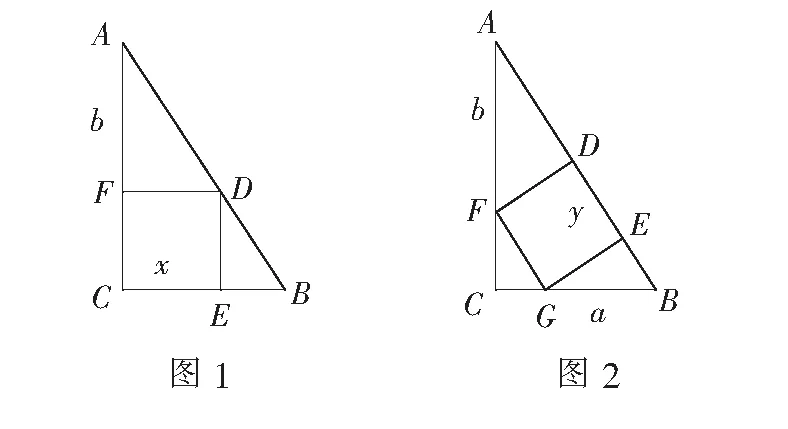
(2)比较两种方式,在直角三角形内,哪一种内接正方形面积最大?

评析本习题基于人教A版第2章“一元二次函数、方程与不等式”的内容，进行“基本不等式”的知识考查.基本不等式结构简单,关系深刻,在高中数学中有着举足轻重的地位．以上借助“勾股容方”问题设计分层问题,一是数学史是数学教学的指南；二是在基本不等式的教学中,配套习题多为常规的应用题,简单的证明题,使用有数学史料的习题,可加深学生的数学理解,帮助学生对比古今思想方法,拓宽学生的数学思维,在渗透数学文化的同时,进行数学文化的再创造．

三、小结与反思

1.不必片面追求“大容量”练习

作为新题型的一种,数学阅读理解题是考查学生数学能力的一种形式,往往在表述上有较大的阅读量,很多教师为了迎合当下命题趋势,在命题上常常对“一手阅读材料”简单下移式处理,视觉上显现“大容量”,形式上貌似“大手笔”,这是风格的坚守还是命题的八股呢?正如章建跃教授所言:真正的数学题应该满足一些基本条件,例如，反映数学本质,与重要的数学概念和性质相关,不纠缠于细枝末节,体现基础知识和联系性,解题方法自然、多样,具有发展性,表述形式简洁、流畅且好懂等特点．在编拟习题时,一方面坚决落实知识、能力的考查需求,另一方面需要因题而异,因知识点而异,对细枝末节进行适当的修剪．不必刻意只关注理解能力考查,理解能力的考查也不必只体现在文字阅读量及其理解上．

2.注重教学导向

编拟配套课本的数学阅读理解题,不仅仅是为了让学生适应“材料——阅读”的模式,更应该借助由教师的精心设计将“冰冷的美丽”转化为“火热的思考”．可以是利用“材料”设计问题链形式,深挖变式,巩固知识,也可以是利用阅读理解题引导学生阅读自学,带着数学的眼光,学会一种思路,学习一种方法．“教师不应是教课本而是用课本去教”,充分发挥课本练习的功能,在教学上狠下功夫,提升学生关键能力．要创造条件,给学生阅读空间．四基四能的核心在于活动平台,在观念上改变过度(刻意挖掘深度)的机械训练;另外，还要重视学生基本综合能力,从阅读的知识迁移到创新层面进行能力培养,引领学生的思维再上更高的台阶．

3.辩证理解“新”与“旧”

新题型中的“新”是一个相对概念,几年后也许不能再称为“新”了．这些题型有什么教育教学价值?这些题型如何设计?如何教学?如何评价?……从这个角度看,传统题型教育教学有太多的优势,而新题型教育教学又有太多的不足,但这条路总应该有人去开拓、去探路,愿做探索之路上一块小小的路标．从某种意义上说，数学传统题型教育教学的优势之处也就是它相对的劣势之处,新题型教育教学的成功之处也就是它相对的不足之处.可以断言两者的有机结合一定会超越任何一方,是更适应当代社会需求的教与学[6].