考虑碳减排的综合能源服务商合作运行优化策略

王 琦，李 宁，顾 欣，何国鑫，杨冬梅，陈 严

（1. 南京师范大学南瑞电气与自动化工程学院，江苏省 南京市 210046；2. 国电南瑞科技股份有限公司，江苏省 南京市 211106）

0 引言

实现碳达峰和碳中和（以下简称双碳）是一场深刻的社会系统性变革［1］，能源行业作为中国碳排放的主要来源之一，其转型对实现双碳目标至关重要，而构建综合能源系统则为减少碳排放提供了一条有效途径［2-3］。

通过建设能源互联网可以助力碳减排目标［4-5］，从系统运行出发，常用的方法包括考虑碳排放经济性惩罚［6］、考虑碳排放约束［7］、考虑碳交易机制［8］等。文献［6］考虑碳排放量建立了多个独立运营商的低碳经济调度模型，按照排放量给予经济惩罚。文献［7］建立了含碳排放限额约束的虚拟电厂日前调度模型。文献［8］基于碳交易机制建立了虚拟电厂的低碳经济运行模型。这些方法对于促进碳减排均有一定的效果，但是处理方式比较单一，难以调动多方参与的积极性，不能有效地从整体上减少社会总碳排，因而进一步出现了多种手段联合进行碳减排的研究成果［9-10］。文献［9］结合碳捕集技术和碳交易机制，建立了以综合成本最低为目标的电-热-气综合能源系统调度模型。文献［10］通过结合碳交易机制和可再生能源证书交易机制以促进碳减排。上述研究仍主要是从供能侧考虑问题，没有从需求侧考虑到多利益主体能量共享的潜力。

在区域能源互联网中，综合能源服务商（以下简称主体）具有从需求侧控制和减少碳排放量的巨大潜力，多个主体的互联互通不仅可以通过能源交易提升区域的经济性和供能灵活性［11］，还可以促进碳减排，进一步提升社会效益。

目前，主体参与市场交易运行的模式主要是分布式调控［12-13］。文献［12］考虑了电网运营商、气网运营商和能源枢纽的独立性，构建了基于交替方向乘子法的分布式运行框架。文献［13］将㶲损优化目标引入到多能枢纽的分布式优化调度中，从而实现能源的高效率利用。但是，分布式调控在缺少监管时，单个利益主体可能仅考虑自身优化目标，忽略系统的整体情况。因此，兼顾底层各利益主体自主协同交易，同时考虑顶层监管的双层协同调控模式优势明显，顶层的监管中心可以起到整体协调碳减排的功能。

主体参与市场运行涉及多主体间的利益矛盾，为避免出现无序竞争，已有学者采用博弈理论［14-16］处理其利益关系。文献［14］基于Nash 议价理论构建了主动配电网的能量交易模型。文献［15］基于Stackelberg 博弈理论建立了多综合能源园区运营商与供需双侧博弈互动的交易决策模型。文献［16］基于非合作博弈理论建立了多综合能源园区的优化模型。但是，上述研究成果大多关注了多主体间的博弈竞争行为，或者仅考虑了合作运行时能源交易的经济性最优，没有考虑多种能源能量共享可以进一步挖掘主体促进碳减排的潜力。

鉴于此，本文提出了双层协同优化架构下基于Nash 议价理论主体合作参与日前能源交易的运行优化调度方法。首先，提出了可以解决主体响应碳减排问题的双层协同优化运行架构，其中顶层的集中监管中心制定交易规则、审核碳排放标准，底层的利益主体在监管下交互有限信息完成协同优化。其次，构建了考虑碳减排的多主体合作博弈模型，通过求解得到能量交易结果和交易价格。最后，进行了惩罚系数和碳排放限额的灵敏度分析，通过算例验证本文所提方法的有效性。

1 双层协同优化运行架构

顶层的集中监管中心降低了传统集中计算平台的计算压力，由“掌权者”变为“监管者”。集中监管中心不再接触底层各利益主体的隐私数据，不再涉及复杂的数据计算，仅通过经济、安全、环保指标对底层各利益主体的交易和调度行为进行监管。本文重点关注主体合作运行时的碳排放量，根据当前发展水平设置合适的碳监管标准，通过合作运行促进碳减排；侧重研究合作运行中的经济调度。若调度过程中产生网络堵塞问题，可以通过顶层监管层的潮流监管功能解决，不在本文进行讨论。此外，常用的监管指标还包括交易量［17］、峰谷差率等。

底层的各利益主体均配置具有计算功能的分布式软控制器实现分散自治和自律协同。随着能源互联网的发展，以屋顶光伏和电动汽车为代表的供销一体的产消者不断涌现，数据处理的压力和部分数据无法获取导致传统的集中计算方式已经不再适用［5］。底层各主体以分布式模式完成协同计算，既能保证自身隐私数据不泄露，又能充分利用闲置的计算资源，适用于目前数据处理量日益增长的趋势［13-14］。

分布式软控制器的部署方式分为实部署和虚部署。对于运营规模相对较大的主体，如果具有独立的经营能力，可将分布式软控制器按照实部署的方式配置在利益主体侧；对于运营规模较小的利益主体（比如单个储能设备），可以不具备独立的管理能力，将分布式软控制器按照虚部署的方式配置在集中监管中心侧，由集中监管中心为其分配计算资源，并通过分布式软控制器向其下发调度指令。图1 为双层协同优化运行架构，其中主体1 和2 的分布式软控制器为实部署，主体3 的分布式软控制器为虚部署。

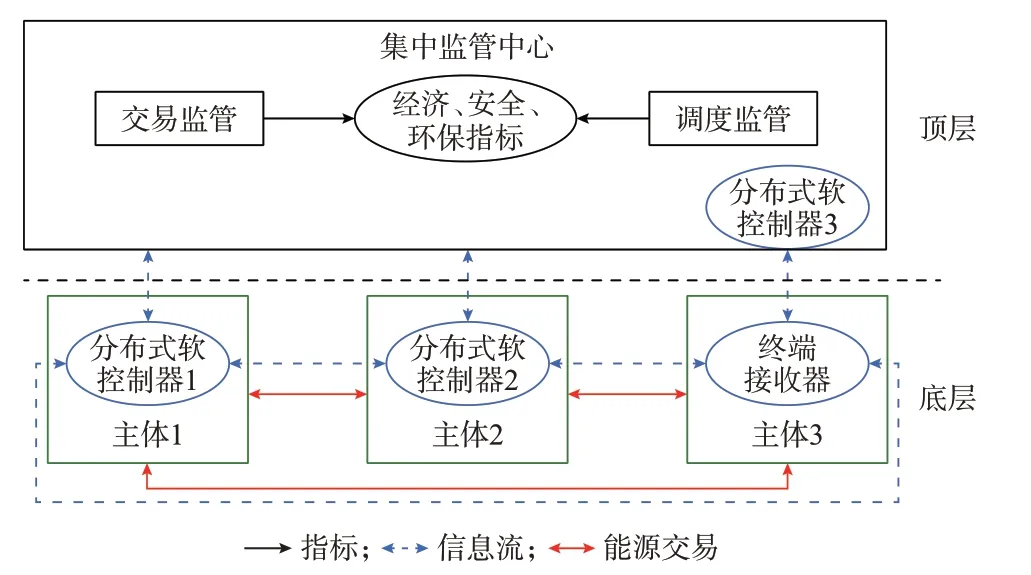
图1 双层协同优化运行架构Fig.1 Two-layer collaborative optimization operation architecture

2 合作运行优化模型

各个主体从属于不同的利益主体，在不考虑各个主体合作运行的情况下，各利益主体分别与上级能源网进行交易，主体可以依靠热电联产（combined heat and power，CHP）机组和区域内的可再生能源供电，大多数时段能够自给自足，在用电高峰期向上级能源网购买电能。集中监管中心按照负荷水平给予主体碳排放量限额，碳排放量超出限额的主体需要缴纳高昂的补偿费用。本文中的碳排放量主要取决于从上级能源网购买的火电量和天然气耗量，非水可再生能源的碳排放量几乎可以忽略不计［8］。

在考虑主体合作运行的情况下，本文假设各个主体以相同的价格从天然气公司购买天然气，在区域能源网中进行电能和热能的议价交易。资源丰富的主体可以把富余的电量和热量通过议价的方式售卖给其他主体，并根据交易量支付相应的传输费用。主体通过合作运行购买的电量和热量不计入自身的碳排放总量；通过电、热交易，部分超额排放的主体可以避免缴纳高昂的补偿费用，出售能量的主体也能获得更高的收益，这种方式既从需求侧限制了社会总碳排放量，也提升了区域热电共融的灵活性，实现了主体的能量、资源共享。能量共享直接体现为电、热能交易量，内部资源共享是由为了满足交易能量的需求而改变内部可调资源的出力计划间接体现。

2.1 目标函数

主体直接面向用户服务，具有一定的生产、传输、储能和转换能力，可以根据自身资源制定相应的日前出力计划，所包含的典型设备有CHP 机组、分散式风电、屋顶光伏、储电设备等。其目标函数为：

2.2 约束条件

1）碳排放限额约束

式中：Pc，i，t-1和Pd，i，t-1分别为电储能设备i 在t-1 时段的充电和放电功率；Pc，i，max和Pc，i，min分别为电储能设备i 充电功率的上限和下限；Pd，i，max和Pd，i，min分别为电储能设备i 放电功率的上限和下限；Ei，t为电储能设备i 在t 时段的储能容量；εi为电储能设备i 的储能自损耗率；ηc，i和ηd，i分别为储能的充、放电效率；Ei，max和Ei，min分别为储能容量的上限和下限；Uc，i，t和Ud，i，t分别为储能t 时段充、放电的状态变量。为了避免设备频繁充放电，在调度周期内限制储能的充放电次数不超过12 次。

4）风电、光伏约束

由于风、光出力具有随机性和波动性，本文采用随机规划方法进行新能源不确定性的描述，包含基于拉丁超立方采样的场景生成和基于同步回代削减技术的场景削减，把生成的1 000 个场景削减为6 个典型场景，并得到相应的发生概率。风、光出力的概率分布均采用正态分布进行模拟，概率距离采用欧氏距离。由于该方法运用已经较为成熟，文中不再赘述，具体步骤可参见文献［18-19］，风电、光伏约束为：

6）端对端（peer-to-peer，P2P)交易模式下的功率平衡约束、交易量不等式约束

3 主体合作运行的Nash 议价模型

主体作为独立且理性的利益个体，希望通过合作博弈提升各自的收益或降低运行成本，更重要的是在有效的监管下减少碳排放量。如何在照顾所有参与主体的利益的前提下确定电能、热能的交易量和交易价格也是需要关注的重点之一。本文采用Nash 议价模型，求得Nash 议价博弈问题的均衡解。

3.1 Nash 议价模型

Nash 议价模型的基础表达式为：

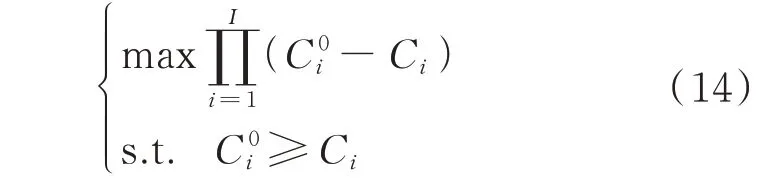
3.2 Nash 议价模型的等效转换

Nash 议价模型需要满足“一正，二定，三相等”［17-18］。“一正”即参与议价交易后，主体i 能从中获益，如式（14）的约束所示。参考文献［17-18］，从已知均值不等式出发，可以将式（14）等效转换为2 个独立求解的凸优化子问题，其详细等效转换过程见附录A。

4 Nash 议价模型求解

基于上文建立的考虑碳减排的主体合作博弈优化模型，采用自适应交替方向乘子法按顺序求解合作效益最大化子问题和能源交易支付子问题。

4.1 自适应交替方向乘子法原理

交替方向乘子法算法的基本原理可参见文献［20-21］。对于式（15）所示的标准形式，先构造增广拉格朗日函数，然后分解为2 个子问题进行交替迭代求解。其详细迭代求解步骤及改进后的自适应更新方法见附录B。

式中：凸函数f (x)和g(z)为待优化的目标函数；A、B、c 为参数；x 和z 为变量。

4.2 合作效益最大化子问题求解

对于主体i，子问题1 的增广拉格朗日函数Li，1(·)的表达式为：

基于自适应交替方向乘子法，各个主体的分布式软控制器重复执行式（17）所示的步骤，直到所有主体均满足收敛条件。其中，设置各个主体的交易量初值均为0。

式中：εpri，1和εdual，1分别为原始残差和对偶残差的收敛精度。

子问题1 求得的最优解为U0i，最优决策变量集合为{qij，qji|i ∈I，j ∈J }。将子问题1 求解得到的结果代入子问题2 继续求解电、热交易价格。

4.3 能源交易支付子问题求解

对于主体i，子问题2 的增广拉格朗日函数Li，2(·)的表达式为：

各个主体的分布式软控制器重复执行的迭代步骤及收敛条件与式（17）和式（18）大致相同，只须替换对应的模型和参数即可。其中，电、热交易价格的初值均为0。

5 算例分析

5.1 基础数据/仿真条件

本文选取中国北方某地区的典型用能场景，选择3 个具有代表性的主体验证所提方法的有效性，为了便于表述，以下简称主体1、主体2 和主体3。在MATLAB 2019b 编译环境下，采用Yalmip 工具建模和Mosek 求解器求解。主体1 和主体2 代表用能密集的核心区，由于核心区的规划特点，不利于安装大容量的非水可再生能源电站［22］，主体1 配置分散式风电，主体2 配置屋顶光伏；主体3 代表有较为丰富的非水可再生能源的非核心区，配置大容量的风电场。算例中，主体1 和主体2 采用实部署方式，主体3 采用虚部署方式。虚部署考虑了各个主体的实际情况，即原有设施基础和投资新建设施成本，主体3 代表用能非核心区。这类区域往往用能密度低、可再生能源资源丰富、地域广，原有设施基础一般比较薄弱或者分布较为分散，投资建设分布式软控制器成本较高。相比之下，租用监管中心的云平台资源更具经济性，且实施难度更小。此外，为了限制主体功率倒送和负荷需求的高峰值，设置2 个主体间的电能、热能交易功率分别不超过600 kW 和300 kW。同时，假设区域能源系统规划合理，各个气源点的天然气供应充足，能满足区域内燃气轮机最大出力的供应需求。

附录C 表C1 为碳排放相关参数及过网传输成本参数；附录C 表C2 为各主体内可调资源的具体参数，其中柔性负荷单位惩罚成本参考文献［23］，考虑到主体3 的用能密度相对较低，所以其柔性负荷成本相比于主体1 和2 较高。附录C 图C1 和图C2分别为各主体的电负荷和热负荷预测曲线；附录C图C3 为各主体的风、光发电预测曲线，实际数据包含预测值与预测误差。采用拉丁超立方抽样方法生成每个风电场和光伏电站的1 000 个新能源出力场景，并通过同步回代削减技术得到附录C 图C4 至图C6 所示的风电场、光伏电站出力的典型场景和相应概率；各主体从上级能源网的购电价格、从天然气公司的购气价格均为阶梯价格，且售电价格为购电价格的50%，具体参数见附录C 图C7。

5.2 仿真结果讨论分析

5.2.1 算法收敛性分析

碳排放限额和惩罚系数是由集中监管中心设置的非固定参数，为了便于比较分析，其余部分选取碳排放总限额为24 t，惩罚系数为180 元/t。附录D 图D1 为子问题1 的算法收敛特性。求解子问题1 时，在第62 次迭代后，所有主体均满足收敛条件，主体1、主体2 和主体3 的成本分别收敛于5 095.23 元、4 196.19 元和2 969.72 元。主体1 至主体3 的原始残差和对偶残差收敛特性见附录D 图D2 和图D3。

交替方向乘子法中，对偶变量λ 和惩罚参数ρ 的初值选取会影响算法的收敛速度，本文选取固定初值［27］（ρ=0.1，λ=0）与自适应交替方向乘子法的收敛性进行对比。如附录D 图D4 所示，在固定初值后，算法收敛速度降低，在约180 次迭代后才接近最优值，在第270 次迭代仍然无法满足收敛的精度要求。与之相比，附录D 图D1 中只须经过20 次迭代就接近最优值，且第62 次迭代后满足收敛精度要求。

5.2.2 惩罚系数和碳排放限额敏感性分析

以主体1 为例，对其惩罚系数和碳排放限额进行敏感性分析。如图2 所示，碳排放限额分别取值10.0 t、10.7 t 和11.0 t。当碳排放限额固定时，若实际碳排放量超出碳排放限额，主体会根据递增的惩罚系数减少实际碳排放量直到达到标准，即实际碳排放量等于碳排放限额，如碳排放限额为11.0 t 的曲线所示，在惩罚系数大于150 元/t 时，实际排放量与限额均等于11.0 t。但是，当调节成本过高时，即使惩罚系数持续增加也很难调动主体减少碳排放的积极性，即实际碳排放量总是大于碳排放限额，如碳排放限额为10.0 t 和10.7 t 的曲线所示。可见，当主体自身的运行成本较大时，较小的惩罚系数无法达到很好的碳减排效果。

图2 惩罚系数敏感性分析Fig.2 Sensitivity analysis of penalty coefficient

如图3 所示，惩罚系数取值分别为120 元/t、180 元/t、210 元/t。当惩罚系数固定时，实际碳排放量“跟随”碳排放限额的减少而递减，但存在一个极限值（实际碳排放量等于碳排放限额）。在合理范围内，惩罚系数越大，实际碳排放量能达到的理论最小值就越小，但是一旦达到这个最小值，即使设置更低的碳排放限额也很难促使实际碳排放量继续减少。上述3 个惩罚系数值对应的实际碳排放量理论最小值分别约为11.15 t、10.95 t 和10.54 t。

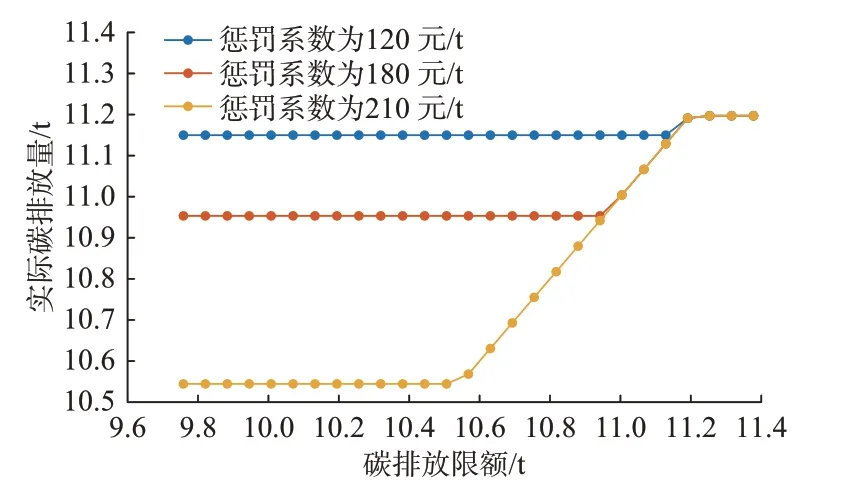
图3 碳排放限额敏感性分析Fig.3 Sensitivity analysis of carbon emission limit

由上述分析可知，仅仅通过单一的设置碳排放限额或惩罚系数的方法很难调动主体减少碳排放的积极性，各个主体反而会从碳交易市场购买大量配额满足自己的需求，或者因高额的碳排放惩罚而产生不满情绪，因此无法从总体上提升社会效益。综上，本文其余部分选取碳排放总限额为24 t，惩罚系数为180 元/t，以方便分析在同样的参数下验证结合区域的热电共融，可以更好地调动主体减少碳排放量的积极性，能从需求侧减少社会的总碳排。

表1 为在不考虑热电交易时，计及碳排惩罚成本前后的总成本和碳排放量对比，其运行结果分别通过求解附录E 式（E1）和式（E2）得到，碳排放量计算方法参见附录E 式（E3）。由表1 可知，因为碳排惩罚成本在总运行成本中的占比较少，主体1 中约为3.84%，主体2 中约为10.61%。因此，在计及碳排惩罚后，主体响应减少碳排放量的积极性不高，总碳排放量仅减少了1.18 t。

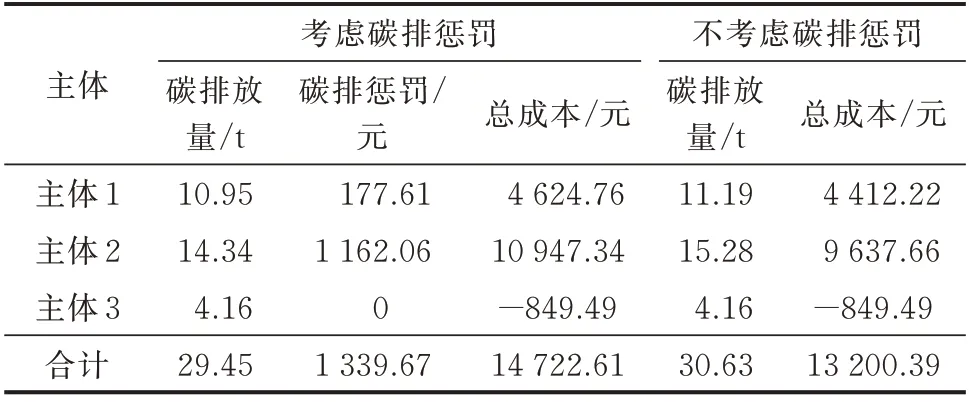
表1 计及碳排惩罚成本前后的运行结果对比Table 1 Comparison of operation results before and after considering penalty cost of carbon emission

5.2.3 主体合作运行电、热能交易分析

附录F 图F1 至图F4 分别为主体1 在议价交易前和议价交易后的最优电、热负荷情况。考虑议价交易前，在白天的用能高峰期，主体1 需要从上级能源网购买大量电能满足自身的用电需求，同时会有一定的削减电负荷和可转移电、热负荷帮助缓解高峰期的用电紧张情况，储电设备以峰谷套利的模式充放电。而在考虑议价交易后，为了满足碳排放标准，主体1 从上级能源网的总购电量和CHP 机组总产出量都降低了，从其他交易主体购买电能和热能进行替代，此处的电能可能是其他主体无法消纳的可再生能源电量或已满足碳排放标准的主体代为从上级能源网购买，然后出售给其他主体。在夜间的用能低谷期，主体1 仍优先与其他主体进行交易，一方面，出售多余的能量可以获取更高的收益；另一方面，部分主体的可再生能源机组以光伏发电机组为主，在夜间购买其他主体的能量可以使之减少从上级能源网的购电量，以及减少从天然气公司的购气量，从而满足自身的碳排放限额标准。此外，主体2和主体3 参与合作议价后的最优电、热负荷情况见附录F 图F5 至图F8。

各个主体的电能、热能交易结果如图4 所示。关于电能交易结果，在白天的用能高峰期，主体1 从主体2 和主体3 购买大量电能，一方面是满足其用能需求，另一方面是为了尽量满足其碳排放限额要求；在夜间用能低谷期，由于主体2 的大量光伏发电机组停发，需要向主体1 和主体3 购买大量电能。关于热能交易结果，在整个调度周期内，因为主体1 有较高的热负荷需求，所以在大多数时段会从主体2和主体3 购买热能。此外，主体3 因为含有大量风电资源，所以在调度周期内几乎都是通过出售电能获得利润；而主体1 和主体2 因为负荷需求和内部资源的差异性，在白天与夜间呈现出了不同的电、热能交易倾向。

图4 能源交易结果Fig.4 Energy trading results

各个主体的电能、热能交易价格如图5 所示。图中，主体1-2 电价表示主体1 从主体2 购买电价。在夜间用能低谷期，主体2 从主体1 和主体3 购买电能的价格一般高于市场价格。这是因为通过合作议价交易获取的能量只计入卖方的碳排放量，而不计入买方的碳排放量。因此，在考虑碳排惩罚后，主体2 为了完成碳减排目标和不支付碳排惩罚，仍然会选择通过议价交易获取能量，而不是从上级能源网购买。

图5 能源交易价格Fig.5 Energy trading prices

5.2.4 主体合作前后运行收益对比析

设置区域碳排放总限额为24 t，根据各个主体的预测负荷量得到单个主体的碳排放限额分别为9.97 t、7.88 t 和6.15 t。

表2 为考虑合作议价前后的碳排放量和总成本对比。合作议价前，主体1 和主体2 均因超出限额需要支付碳排惩罚，金额分别为177.61 元和1 161.05 元，由于碳排惩罚的占比较小或者主体自身可调资源不足，所以很难调动主体减少碳排的积极性。但是，设置高额的惩罚系数既不现实，又不符合各个主体的自身利益，并且因为单个主体的内部可调资源是有限的，即使设置了高额的惩罚系数也未必能达到较好的碳减排效果。合作议价后，主体1 至3 的碳排惩罚费分别为0 元、237.22 元、0 元，主体1 至3 的总成本分别降为3 817.84 元、10 116.17 元、-1 714.13 元。从总收益角度看，假设主体的售能策略不变，即为用户供能的收益不变，通过能量共享的方式，在保障用户用能的情况下降低了自身的运行成本，相当于主体1 至3 的总收益分别提升了805.21 元、831.17 元、864.65 元，均约占总提升收益的1/3，达到了均衡分配合作收益的效果。特别是合作议价后，在同样的碳排放限额和惩罚系数下，总碳排为25.33 t，相比于合作议价前减少了4.12 t，主体1 和主体2 的碳排放量均小于等于设置的碳排放限额，在不需要征收高额碳排惩罚费用的情况下达到了更好的碳减排效果，既从需求侧调动了主体减少碳排放量的积极性，又提升了社会效益。

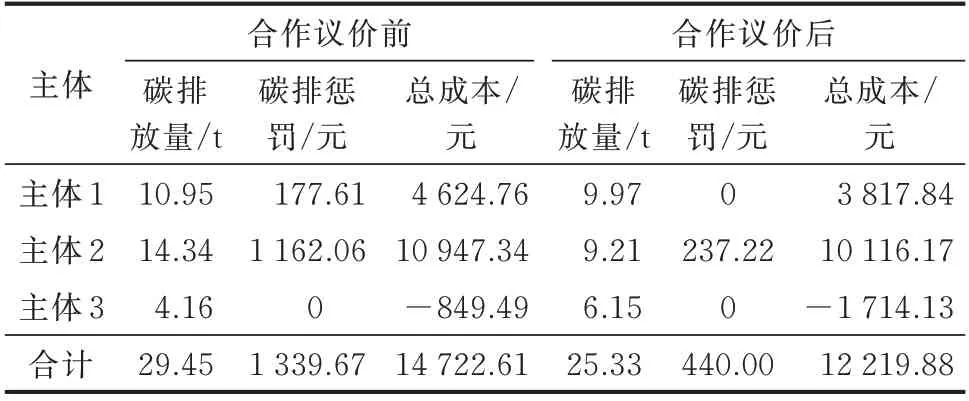
表2 考虑合作议价前后的运行结果对比Table 2 Comparison of operation results before and after considering cooperative bargaining

5.2.5 不同模式下的碳减排效果对比分析

本节在3 个不同模式下，验证它们的碳减排效果，运行结果如表3 所示。其中模式1 采用文献［8］的碳交易机制，模式2 采用文献［6］的碳排放经济性惩罚模型，模式3 为本文所提的基于顶层监管的合作运行模型。为了使3 个模式的横向比较分析具有实际意义，模式1 的碳交易价格、模式2 的CO2惩罚因子和模式3 的惩罚系数均取值为180 元/t，且模式1 的碳排放配额和模式3 的碳排放限额相同。

表3 不同模式下的运行结果对比Table 3 Comparison of operation results in different modes

由表3 可知，在本文设置的算例下模式1 和模式2 的碳减排效果几乎相同。不同的是，在模式1下，主体3 可以通过交易碳排放分配额获得额外的收益，从而提高自身总收益；主体1 和主体2 则需要购买额外的碳排放分配额，额外的碳交易成本将会导致它们总收益减少。在模式2 下，各个主体均需要为全部的碳排放缴纳高额的惩罚费用，从而压缩了它们的盈利空间。相比之下，采用模式3 可以达到更好的碳减排效果，同时各个主体均能通过议价合作降低运行成本或提高总收益。

6 结语

本文为了解决主体响应碳减排积极性不高的问题，构建了基于顶层监管的双层协同优化运行架构；从需求侧角度考虑，设置了主体的碳排放限额和惩罚系数，得到了以下结论：

1）证明了在相同的碳排放限额和惩罚系数下，基于顶层监管的议价合作能够有效地调动主体参与碳减排的积极性。

2）将非凸非线性的合作模型分解为合作效益最大化子问题和能源交易支付子问题，能保证全局经济最优和实现利益均衡分配。同时，采用自适应交替方向乘子法分布式求解，能够保障主体的隐私和提高计算的收敛速度。

3）由于顶层监管的存在，即使在交易价格高于向上级能源网购能价格的时候，主体也可能会为了减少自身碳排放量而优先选择参与议价交易。

4）通过对比分析碳交易机制模式、碳排放经济性惩罚模式、基于顶层监管的合作运行模式下的运行结果，证明了本文所提方法在促进碳减排、提升区域经济性、环保性方面的优势。

鉴于目前碳交易市场交易价格较低，无法从需求侧有效减少社会总碳排放量的窘境，本文所提方法可以作为进入碳交易市场前的辅助手段，有效地调动主体参与碳减排的积极性。本文仅考虑了多主体合作运行的经济行为，未涉及能源网的安全、可靠运行，具有局限性。在后续研究中，将进一步考虑网络堵塞等因素，针对计及电网、热网运行约束的潮流监管问题开展更深入的研究，同时考虑多重不确定性的合作运行方法也亟待研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。