自适应稀疏度的1 bit压缩重构算法

黄澳 柏正尧，2 周 雪

（1.云南大学信息学院，云南昆明 650500；2.云南大学-云南天文台信息技术联合实验室，云南昆明 650500）

1 引言

在过去的几十年里，数字处理技术的发展刺激了对更大带宽信号和更高分辨率图像和视频的数字化需求的快速增长。然而，传统ADC 设备无法满足这种带宽数字化的需求。为了解决这个问题，一种不同的数据采集框架，即压缩感知（Compressed Sensing，CS）出现了，基于CS 提出的显著性图像可以广泛应用于许多计算机视觉领域的应用，CS利用信号的稀疏特征，能用数目显著低于奈奎斯特采样定理要求的样本准确地重构出稀疏信号。

目前，压缩感知理论在诸多领域都取得了很好的研究成果，但是压缩感知要想从理论走向实际还需要考虑存储、传输和处理等过程。为了降低硬件的复杂性、成本、数据传输带宽和能量，需要用少量的比特来量化测量。因此，一些学者提出了1位CS，利用每个被测符号进行1 bit量化，恢复稀疏信号，提高信号采样效率。2007 年，Boufouno 和Baraniuk 等人［1］提出了一种基于不定点迭代（Fixed-Point Continuation，FPC）的算法--重正规化不动点迭代算法（Renormalized Fixed Point Iteration，RFPI），该算法利用单边的l2范数来强制一致性。该算法是有效的，但出现符号跳变时表现不佳。除了基于FPC的方法外，还提出了其他一些1位CS算法，包括二进制迭代硬阈值（Binary Iterative Hard Thresholding，BIHT）［2］、匹配符号追踪（Matching Sign Puisit，MSP）［3］、基于正交匹配追踪（Orthogonal Matching Pursuit，OMP）［4］的量化子空间追踪（Quantization Subspace Pursuit，QSP）与量化压缩采样（Quantization Compressive Sampling Matching Pursuit，QCaSamp）［5］、基于l1最小化线性回归（Linear Programming，LP）［6］、历史（HISTORY）算法［7］、被动（passive）算法［8］和类似于信赖域的限制步长收缩算法RSS［9］。这些算法或多或少都有缺陷。QSP、QCasamp、QMP、BIHT、MSP 和HISTORY 这些需要稀疏性水平作为先验信息，而RFPI、passive 和RSS 则不需要。另外，BIHT 在重建误差和一致性方面优于MSP和RSS。

对1 bit 压缩感知的另一个挑战是噪声环境下的鲁棒性。在有噪声的情况下，二进制测量值是随机扰动的，符号跳变严重降低了恢复性能。文献［10］提出的自适应异常值追踪（Adaptive Outlier Pursuit，AOP）算法，以及基于RFPI 与自适应异常值追踪的NARFPI［11］算法在噪声环境中具有鲁棒性。尽管这些信号重构算法具有良好的性能，但无一例外都需要信号稀疏性这一先验信息。因此，一些研究者致力于通过克服稀疏依赖性来提高信号恢复的精度，文献［12］提出一种基于AOP 思想的改进不动点的FPC-AOP-算法，它虽然不需要信号稀疏度的先验知识，但性能不理想。另外，用于处理符号跳变错误的鲁棒的1 bit 贝叶斯压缩感知（Bayesian Compressed Sensing，BCS）［13］，信号重构性能良好且不需要信号的稀疏度先验信息，但是却需要稀疏信号与噪声的高斯逆伽马先验信息。文献［14］提出分块稀疏信号重构算法，性能优于BIHT 算法，但由于需要计算Toeplitz 矩阵，计算效率不高，适用于维度比较低的稀疏信号重构。文献［15］考虑超定与欠定条件下的最小二乘法，引入一种原始对偶活动集算法，提出原对偶连续主动集算法（A primal dual active set algorithm with continuation，Pdasc）算法来解决非平滑问题，对噪声和符号跳变具有一定鲁棒性，然而只对稀疏度较低有效，但对于稀疏度高的问题重构性能不佳。文献［16］提出非凸稀疏性的诱导惩罚型算法，极大最小的凸惩罚项（Minimax Concave Penalty，MCP），求解对偶问题，来求得解析解。能够获得较好的结果并提高恢复性能。但对噪声鲁棒性不高，而且对于低维信号性能不佳。总之这些算法要么需要稀疏性水平的先验信息，要么信号重构性能有限。

针对上述方法的局限性，本文提供出一种简单而有效的算法，在稀疏性未知的情况下，借鉴稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）［17］自适应稀疏度思想，结合自适应异常值追踪与自适应稀疏度的思想实现最优的信号重构性能。自适应异常值追踪能够检测出大部分的符号跳变，并且在符号跳变被纠正后，测量结果更加准确，因此能够提高这算法的性能。本文方法利用弹球损失函数，提高对符号跳转的检测，此外，还设置了正则化参数，以加快运算速度。与现有算法相比，该算法的性能有显著提高。数值结果表明了该算法的有效性和优越性。

2 压缩感知理论

2.1 一位压缩感知理论

压缩感知是稀疏可压缩信号采样和重构的一种方法。不失一般性，假设信号x是N 维向量，稀疏度为K，通过采样，得到信号y=Φx，要从y中重构信号x：

一位压缩感知问题变为：

信号的幅度通过一位量化丢失，将稀疏信号限制在超球面上，

二进制迭代硬阈值算法（BIHT）是在迭代硬阈值算法（IHT）的基础上提出的。在经典压缩感知中，引入IHT对稀疏信号进行迭代重构。

IHT 方法用于解决压缩感知中的类似以下的问题：

IHT迭代公式有：

其中ηK(x)，通过保持K个最大的项的大小为x，suppK(x)其余设置为0。

类似地，在1 位压缩感知中，BIHT 修改IHT 中的梯度步骤，迭代计算如下：

BIHT算法可以看做是解决这样一个问题：

[·]-是负值函数，大于零的元素取零，负数不变（单边l1范数）。

BIHT 算法在无噪声的情况下能得到更好的可行解。但是如果有许多测量信号值发生跳变，BIHT的效果变得很不理想。

假设噪声级别（发生跳变的信号所占比例）给定，我们可以选择一个合适的整数L，整个测量值中最多有L个信号被错误地采集（发生跳变）。比如测量值y∈{-1，+1}M，Λ∈RM是一个二值矢量表示数据的对错：

我们可以把我们的问题表述为：

自适应离群点追踪的求解，采用交替极小化方法［10］求解：

（1）固定Λ，求解x：

（2）固定x，求解Λ：

这个问题可以从[y·(Φx)]-的M个元素中选择M-L个元素，这些元素满足和最小。对于问题一中估计出来的x，我们在一步中更新Λ：

T是[y·(Φx)]-中的第L大的元素值。

BIHT-AOP算法的是为了找到ΦT(y-sign(Φx))的最小值。采用梯度下降法求出最小值，通过硬阈值函数映射到单位球面上。交替极小化法，求解原稀疏信号。

本文首先使用高斯稀疏信号作为原始信号进行仿真实验。信号长度N=1000，M=500，信号噪声比例50 dB，跳变次数L从10到100，间隔为10，感知矩阵Φ为随机高斯矩阵。使用BIHT-AOP重构。在不同稀疏度下，L从10 到100 时，进行100 次实验。实验结果如图1 所示，在信号跳变固定下，稀疏度K未知下，不同稀疏度对重构信号的精度影响较大。相同稀疏度下，信号跳变越多，重构信号信噪比也就越低。通过上述实验结果分析，稀疏度K与噪声是影响重构效果的两个重要因素，为了提高重构信号信噪比，有必要去解决对稀疏信号的稀疏度K的依赖以及提升对信号噪声鲁棒性。

2.2 自适应稀疏度的一位压缩感知算法

我们将固定步长自适应方法与自适应异常值追踪引入PIHT 算法中，提出了一种自适应稀疏度的AOP-ASPIHT算法，用于解决未知信号稀疏度与符号跳变导致的重构效果不理想的问题。其中，固定步长法主要是通过计算得到信号稀疏度的估计数，然后将估计数输入到算法中，进行下一步的信号部分恢复。

首先定义弹球损失：

文献［18］给出了以下关于一位压缩感知的凸模型：

在无噪声情况下，PIHT 算法相对BIHT 有所提高。但如果有信号跳变，两种算法效果都变得不理想。为此加入自适应异常值追踪。变为下述问题：

首先设定初始步长m＜K作为迭代的初始硬阈值参数，然后判断相邻两次迭代信号的能量差和残差大小，确保迭代向收敛方向发展。

当相邻两次迭代信号的能量差小于ε时，此时的硬阈值大小（估计稀疏度S）最接近信号稀疏度，再利用S恢复原信号。步骤（1）到步骤（3），实现了稀疏度的粗估计和迭代变量的初始化。详细如表1所示算法1。

表1 本文提出算法伪代码Tab.1 The pseudo-code of the proposed algorithm in this paper

（1）确定固定步长m，使其满足m＜K。

（2）采用步长m值的大小作为硬阈值的初始值在球面映射重建。通过计算相邻两次迭代过程中信号估计值的能量差和残差，判断残差是否随迭代次数的增加而减小，计算出两个信号的能量差小于ε。

（3）记录此时硬阈值的大小，并将其用作估计的信号稀疏度以用于信号恢复。

3 实验仿真与结果分析

3.1 对AOP-ASPIHT仿真

我们在i5-7500，GTX750ti 电脑上用Matlab R2020a软件进行仿真实验，比较了有（无）噪声影响下算法的信号重构性能。实验中的信号恢复性能指标主要基于主流的评价指标，信噪比（Signal Noise Ratio，SNR）和均方误差（Mean Square Error，MSE），绝对均方误差（Absolute Mean Square Error，AMSE）与汉明误差（Hamming Error），其中信噪比定义如下：

均方误差（MSE）定义如下：

绝对均方误差（AMSE）定义如下：

汉明误差（HE）定义如下：

3.2 无噪声影响下算法性能比较

感知矩阵Φ全部使用随机高斯矩阵。其中，模拟信号的长度固定在N=256，观测次数M=100，稀疏度K=10，AOP-ASPIHT 参数步长m=5。比较在符号跳变率为0%（无符号跳变），无噪声，稀疏度为10时，BIHT 重构算法，归一化二进制迭代硬阈值（Normalized Binary Iterative Hard Thresholding，NBIHT）［19］，PIHT［3］，以及本文提出的AOP-ASPIHT 的均方误差（MSE），信噪比（SNR）以及运行时间。进行了100次蒙特卡洛实验。

文献［19］证明了最佳误差衰减率取参数μ=得到归一化二进制迭代硬阈值NBIHT 算法，将BIHT 中损失函数换为弹球损失函数，得到PIHT。仿真实验结果如表2 所示，在无噪声，无符号跳变下，NBIHT 算法性能相对BIHT 算法并没有提高，但是运行时间少于BIHT算法。PIHT算法信号重构性能是优于BIHT 算法，MSE 减低2.1%，信噪比提高5.13%，运行时间减少约BIHT 的1/6。PIHT（α=，将BIHT 算法中μ值设置为μ=性能相对PIHT（α=0.05）有所提升，本文提出的AOP-ASPIHT算法重构性能明显优于PIHT，BIHT。相对BIHT，MSE 降低9.72%，信噪比提高17.09%，运行时间减少约BIHT 的1/3。在无噪声情况下，PIHT 相对BIHT 算法重构性能有所提升，NBIHT 算法相对BIHT 运行时间有所降低。为此考虑在下一步有噪声实验中加入归一化参数。

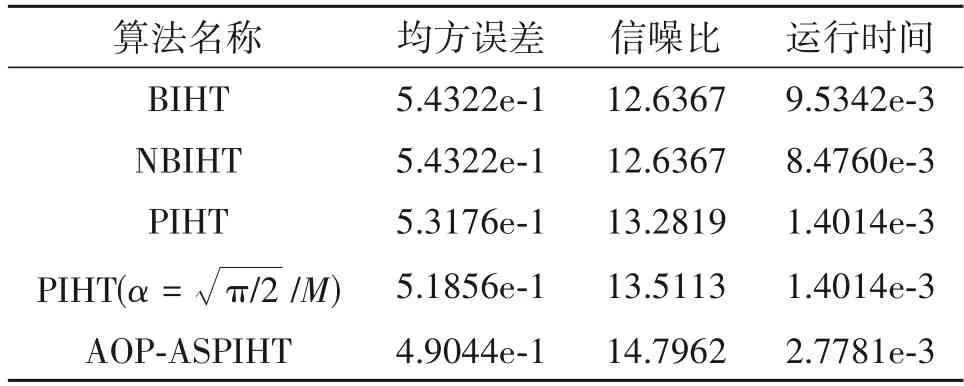
表2 四种算法性能比较Tab.2 Performance comparison of four algorithms

3.3 有噪声影响下算法性能比较

采用AMSE，SNR，HE 与运行时间等指标对PIHT［3］，BIHT-AOP［10］，PIHT-AOP［3］及本文提出的AOP-ASPIHT 算法重构性能进行比较。模拟信号采用经典的高斯稀疏信号。稀疏信号固定长度N=1000，观测次数M从200 到700，间隔为100。稀疏度设置K为10，符号跳变比例5%～10%（稀疏信号中有M× 10%个符号跳变）。PIHT，BIHT-AOP，PIHTAOP以及本文提出的AOP-ASPIHT步长参数均设置为

为验证AOP-ASPIHT 算法性能重构性能，利用BIHT 算法，BIHT-AOP 算法，PIHT-AOP 以及本文提出的AOP-ASPIHT对信号进行重构，比较其绝对均方误差，信噪比，汉明误差以及运行时间。由图2（a），（b）以及图3 四种算法汉明误差，运行时间的对比，可以看出本文提出的算法信号重构性能要优于PIHT，BIHT-AOP，PIHT-AOP，在测量值M=300 时，相对PIHT-AOP 算法本文提出算法绝对均方误差降低约0.15，信噪比提高约5 dB，汉明误差降低约0.04。这说明本文提出方法可以有效地降低符号跳变对重构信号的性能的影响。M值超过600之后本文提出方法重构性能SNR 随着测量值增加，增长变缓慢。由图3（b）看出，BIHT-AOP 算法由于在算法过程中增加了对符号跳变位置的检测，消耗了时间，其运行时间增加。在M=400 时，运行时间超过本文提出的AOP-ASPIHT。PIHT 算法可以降低符号跳变的影响，加入自适应异常值追踪方法后，可以进一步降低符号跳变的影响使得算法收敛速度快。本文提出的AOP-ASPIHT算法利用了相邻残差能量信息，虽然增加了对稀疏度的估计，但是可以使得迭代次数降低，算法收敛速度相对BIHT-AOP加快。

为验证符号跳变比例对信号重构性能的影响，本文考虑M=500，N=1000，K=10。符号跳变比例为5%到10%，每次增长1%。实验结果如图4 跳变对信噪比的影响所示，跳变比例在5%四种算法SNR差别不大。随着跳变比例增加，四种算法SNR 均降低，AOP-ASPIHT 信噪比下降最慢，其次是PIHTAOP，再其次是BIHT-AOP，说明PIHT 算法本身就能减小符号跳变的影响，主要是因为PIHT 通过设计边缘距离来抑制符号跳变对信号稀疏重构的影响。本文所提出的AOP-ASPIHT 利用回溯思想，来估计信号稀疏度的有助于检测符号跳变的位置，其性能提高。从图4可以看出，符号跳变比例10%时，AOP-ASPIHT 信噪比相对提高3 dB。说明本文提出的方法可以更好的抗符号跳变引起的噪声。

3.4 与其他先进算法性能比较

采用MSE 与运行时间等指标对其他先进算法如BIHT［1］，BIHT-AOP［10］，LP［26］，Passive［8］，Pdasc［15］等及本文提出的AOP-ASPIHT算法重构性能进行比较。其中BIHT，BIHT-AOP，LP 均需要稀疏度先验信息，Pdasc，Passive 以及本文提出的方法均不需要稀疏度水平。模拟信号采用经典的高斯稀疏信号。稀疏信号固定长度N=1000，观测次数M从300 到600，间隔为50。稀疏度设置K为10，符号跳变比例分别为1%～10%与2%到14%（稀疏信号中有M×符号跳变比例个符号跳变）。其中BIHT，BIHTAOP，以及本文提出的AOP-ASPIHT 步长参数均设置为

为验证AOP-ASPIHT 算法性能重构性能，利用BIHT，BIHT-AOP，LP，Passive，MCP，Pdasc 以及本文提出的AOP-ASPIHT 对信号进行重构，比较其均方误差与信噪比。稀疏信号固定长度N=1000，观测次数M从300 到600，间隔为50。稀疏度设置K为10，符号跳变比例1%，噪声比例为0.1。由图5（c），（d）看出，本文提出的算法信号重构性能要优于BIHT，BIHT-AOP，LP，Passive，MCP，Pdasc，在测量值M=450时，相对BIHT-AOP算法本文提出算法绝对均方误差降低约0.02，信噪比提高约5 dB。这说明本文提出算法可以有效地降低符号跳变对重构信号的性能的影响且对低M值的稀疏信号有较好的恢复特性。M值超过600 之后本文提出算法重构性能SNR 达到51 dB，其余各种算法随着M的增大，恢复效果逐渐增强，可以最高达到45 dB。原因是PIHT算法本身就能减小符号跳转的影响，加入自适应异常值追踪方法后，可以进一步降低符号跳变，此外利用回溯思想，来估计信号稀疏度的有助于检测符号跳变的位置，其性能提高。且本文算法不易受M值的影响，其余如LP，Passive，MCP，Pdasc 各种算法受M值影响较大，小M值甚至不能很好的恢复稀疏信号。说明本文提出的方法对噪声具有较好的鲁棒性。

为验证符号跳变比例对信号重构性能的影响，本文考虑首先考虑小M值，M=300，N=1000，K=10符号跳变比例为1%到10%，每次增长1%。实验结果如图5（a）所示，跳变比例在1%，性能相对最好的PDASC 算法重构成功率约为0.75，此时本文所提算法重构成功率达到1。随着跳变比例增加，七种算法重构成功率均降低，AOP-ASPIHT 算法重构成功率下降最慢，其次是BIHT-AOP。主要因为本文所提出的AOP-ASPIHT 利用回溯思想，来估计信号稀疏度的有助于检测符号跳变的位置，此外还通过设计边缘距离来抑制符号跳变对信号稀疏重构的影响，其性能相对BIHT-AOP 提高。其余算法都能一定程度抑制符号跳变引起的噪声，但性能随着跳变比例的增大，信号重构成功率逐渐降低，在4%时，几乎其他算法信号重构成功率接近0。说明其他算法能一定抗符号跳变，但随着符号跳变比例增大，性能逐步下降。本文所提算法能很好解决符号跳变引起的信号恢复性能不佳的问题。其次本文考虑M值对其他算法如LP，Passive，MCP，Pdasc 恢复性能影响较大，设计如下实验。M=600，N=1000，K=10 符号跳变比例为2%到14%，每次增长2%。实验结果如图5（b）所示，LP，Passive，MCP，Pdasc，BIHT重构成功率都相对M=300 时的重构成功率有所提高，说明随着M值增加，各类算法都具有一定的抗符号跳变能力，但随着符号跳变比例增大，重构性能都下降。在12%时，几乎其他算法信号重构成功率接近0，而本文算法信号重构成功率依然接近0.6。说明本文提出的算法对符号跳变引起的噪声具有很好的鲁棒性。

4 结论

我们提出了具有自适应稀疏性的1 bit压缩感知算法。通过计算残差能量大小，有效地学习了信号和噪声，采用固定步长学习硬阈值参数，近似计算稀疏度，引入AOP 进一步降低符号跳变的影响，获得了满意的结果。通过均方误差（MSE），信噪比，绝对均方误差（AMSE）和重构成功率分析，说明本文提出的1 bit 压缩感知重建算法是有效的，并具有对噪声的鲁棒性。本文重构算法很好地解决了重构算法稀疏度依赖性问题，显著提升了重构效果。

在未来的工作中，我们计划将算法应用于天文射电信号功率谱估计研究中。