多旋翼无人机载SAR视线向运动误差补偿方法
黎涛 付耀文 张健丰 张文鹏 杨威
(国防科技大学电子科学学院智能感知系,湖南长沙 410003)
1 引言
合成孔径雷达(Synthetic aperture radar,SAR)是一种成像雷达,能在低能见度和恶劣复杂环境的条件下对目标区域实行侦察监视,并得到类似光学照相的高分辨率图像,在国土测量、海洋监视、资源勘探、地形测绘、灾情普查、城市规划以及军事侦察等领域发挥着重要的作用[1]。随着微小型无人机技术的发展,微小型无人机载SAR 成为了研究热点[2]。多旋翼无人机作为一种小型无人机,相较于固定翼飞行器,具有起降灵活、便于携带的优点,将SAR 搭载在多旋翼无人机上能实现更为便捷的雷达成像。然而多旋翼无人机相较于固定翼飞机,飞行高度较低,周围气流更为紊乱,且自身质量较小更易受气流影响,故多旋翼无人机载SAR 相较于固定翼机载SAR要面临更严重的运动误差[3]。
运动补偿是SAR 成像中必不可少的一步。运动补偿可分为基于运动参数的补偿和自聚焦,两者不能相互替代。尽管目前自聚焦能补偿基于IMU数据未补偿完善的误差,但目前的自聚焦算法依然受限制较多、补偿能力有限,如PGA[4]及其改进算法仅能在有强点的条件下估计误差准确;MD 算法仅补偿二次项误差,其改进算法多孔径偏移算法[5]估计误差时受多项式模型限制,精度达不到要求;而基于度量函数的自聚焦[6]是较稳健的一类自聚焦算法,然而它的计算耗时较长,且在补偿精度不变的前提下其计算耗时会随着误差的增大而增大。故在追求高分辨率成像时,应首先提高基于运动参数的补偿的精度。传统的基于运动参数的补偿方式为“两步运动补偿法”[7],它对于较大型的固定翼机载SAR 具有较好的补偿效果,但其中包含较多的近似,且未考虑调频连续波雷达脉内运动误差的影响,并不能适用于FMCW SAR。文献[8]考虑了脉内运动的影响,提出了针对FMCW SAR 的两步运动补偿法,但补偿时并未严格区分航向误差和LOS 向误差。文献[9]指出FMCW SAR 的航向运动误差和平动误差可分开补偿。文献[10]将第二步补偿的次序调整至距离压缩后、距离单元徙动校正(Range cell migration correction,RCMC)前,去除了空变相位误差对RCMC 的影响。然而以上算法均是以“两步运动补偿法”为基础,将误差的空变部分的补偿放在距离压缩后,是不精确的。
本文指出了“两步运动补偿法”以及其改进算法应用于多旋翼无人机载SAR 运动补偿时一些近似带来的影响,并提出一种新的基于运动参数的补偿方法,用以更充分地校正视线向(Line of sight,LOS)误差在距离向空变的部分,最后以仿真验证所提方法的性能。
2 信号模型
设某一目标的坐标为(xn,yn,zn),由于本文主要解决LOS 向误差,且无人机航向误差和LOS 向误差可分开补偿[9],故本模型默认无人机在航向上匀速飞行。多旋翼无人机载SAR 成像的几何模型如图1所示。
无人机的航迹为:
其中Vx是无人机航向速度。
雷达从发射到接收该目标回波的时间间隔τ作以下近似:
tm表示慢时间,t^为快时间,R(tm,^)表示对应时刻雷达到目标的斜距。由于无人机载SAR 一般为FMCW SAR,需要考虑脉内运动的影响。R0(tm,)为理想的点到雷达的距离,可表示为:
由于运动误差的存在,真实的点到雷达的距离为R(tm,^),可表示为:
本文假设所有目标均处于平面上,即zn=0。设无人机的速度在一个脉冲周期内(一般小于1 ms)可近似为不变,在各轴上的速度分别表示为Vx,Vy(tm),Vz(tm),故式(4)可表示为:
其中θf为俯视角,θs为目标(xn,yn,0)的方位角,即“雷达-目标”射线在XOY 平面的投影到Y轴角度。为便于讨论,以下均假设雷达波束的方位向宽度较窄,可不考虑宽波束的影响。在正侧视的前提下,cosθs≈1,而sinθs较小,可将^忽略。
设ς(tm)=sinθfVz(tm)-cosθfVy(tm),R(tm,0)=R0(tm,0)+Δr,其中,Δr(tm)表示为斜距误差,将R0(tm,0)简写为R0(tm),于是雷达至目标的斜距可表示为:
雷达接收的回波可表示为
其中wa[·]为方位向包络,wr[·]为距离向包络,L为孔径长度,Tp为脉冲宽度。
由于无人机载SAR一般为dechirp解调,故其回波信号需要乘以参考信号可表示为以下函数:
点目标的回波乘以参考信号后,得到如下混频信号:
将(8)代入(10),点目标回波信号可如下表示
而无误差的点目标回波信号为
式(12)中,wr[·]中的误差难以校正且一般不处理,而相位中的误差可以校正。式(11)相位误差表示如下:
fr为距离向FT后距离向的频率点。
3 两步运动补偿法及其改进
假设方位向波束宽度较小,且雷达在正侧视模式下工作。“两步运动补偿法”在第一步补偿中从原始的回波信号中去除“距离非空变”的误差,在第二步补偿中去除残余的相位误差。
3.1 第一步补偿
当H>>ΔH且yc>>ΔY时,
其中θfc为场景中心对应的雷达俯视角。该近似在实际应用中能加快斜距误差计算速度,然而对于多旋翼无人机等小型无人机,成像距离较短,故式(16)中的近似带来的误差有时不能忽略。非空变的速度误差为ςc(tm),可表示如下。
则第一步补偿中,回波需乘以下式:
设Δrres(tm)=Δr(tm)-Δrc(tm),ςres(tm)=ς(tm)-ςc(tm),残余的相位误差为:
Δφres亦即误差的“空变”部分。
3.2 第二步补偿
“两步运动补偿法”假设经过第一步补偿,距离压缩后目标的包络已处于正确的位置。对于dechirp接收的SAR 系统,“两步运动补偿法”的第二步补偿在RCMC 后的“距离频域-方位时域”进行。此步骤中,Δφres中的“时变”部分被忽略,仅“时不变”误差被校正。校正函数为:
Δrres(tm;fr)即雷达相对于fr对应的距离单元上目标的残余平动误差。至此,式(14)中仍未被校正的相位误差为:
3.3 “两步运动补偿法”局限及其改进
“两步运动补偿法”忽略了第一步补偿后剩余误差中“时变”的部分,即默认为第二步补偿前,目标距离压缩后的包络已校正到位。然而,“两步运动补偿法”最初是针对一般的机载SAR 提出的,搭载雷达的平台飞行要比多旋翼无人机要稳定,实际应用中使用“两步运动补偿法”补偿多旋翼无人机载SAR 的回波信号时,由于原回波信号中“时变”误差的距离空变性被忽略,故距离压缩后非场景中心处的其他目标的包络仍存在误差,此时进行“距离单元徙动校正”后目标的包络并不能被校正至准确的位置上,这将影响之后的方位压缩,也将影响第二步补偿。以一SAR 系统为例[11],设无人机的飞行高度为100 m,下视角为45°,正侧视,距离分辨率为0.075 m,ΔY=-0.6 m,ΔH=-0.6 m,则Δrc=0.0025 m,则相对某时刻的雷达,X轴坐标差为-15 m 至15 m、Y轴坐标相差70 m 至130 m 的地面各点对应的Δrres如图2 所示。图中误差在方位向变化不明显,但在距离向上有明显变化。X轴坐标差为0 m 且Y轴坐标相差80 m(斜距128.0625 m)处目标Δrres=-0.09374 m,而方位向距离差为0 m且Y轴坐标相差120 m(斜距156.2050 m)处Δrres=0.07673 m,均大于距离分辨率,显然边缘处目标距离向包络误差无法忽略,而当运动误差中含高频分量时,其距离包络将存在明显“振动”。
此外第一步补偿中“时不变”误差仅“非空变”部分被补偿,剩余的“空变”部分还未被补偿便进行距离徙动校正。由于RCMC 需在方位频域进行,故误差“空变”部分将直接影响回波的方位频谱,继而影响RCMC。在面临高频误差时,该问题尤为严重。以及,对于FMCW SAR 而言,RCMC 是RD 算法或FS算法才有的,而距离徙动算法的成像过程中没有RCMC,第二步补偿便不能进行。针对这两点问题,文献[10]提出在距离压缩后便进行第二步补偿,并将其命名为“单步运动补偿法”,并通过仿真,验证了“单步运动补偿法”对于高频误差,补偿效果较“两步运动补偿法”更好。但该改进方法并未解决“两步运动补偿法”没解决的包络误差问题,仍不是精确的补偿方法。
4 逐距离单元补偿法
不论是“两步运动补偿法”还是“单步运动补偿法”,均未补偿Δφ中“时变”且“空变”的部分,且由于在第一步补偿中未补偿完便进入后续的成像流程,引发了一系列问题,致使“时不变”误差的空变部分也不能被准确补偿。为解决上述问题,本文提出“逐距离单元补偿法”。
各参数几何关系如图3所示:
设理想航迹下,“距离压缩”后第k个距离单元对应的斜距为Rk。在所有斜距为Rk的目标点中,取坐标为(X(tm),yk,0)的点作为参考,其中:
此时运动误差带来的斜距误差为
速度误差为:
将dechirp后的回波乘以下式:
之后对回波做距离向做FT,得到距离压缩后的信号,此时位于第k个距离单元上的目标被精确补偿。而其他目标将随着斜距差异的增大,补偿后的剩余误差增大。故本次补偿后,仅取距离压缩后第k个距离单元的数据作为补偿后的距离压缩结果的第k个距离单元的数据,其余距离单元的数据被舍弃。
“逐距离单元补偿法”流程如图4所示。
事实上,在进行逐点补偿时,第k个距离单元上不仅有位于该距离单元的目标的主瓣,还有附近的目标的旁瓣。但是能量较高的旁瓣都是属于距离较近的目标的旁瓣,这些目标校正后的剩余误差较小,误差可以忽略。
不同于“两步运动补偿法”或“单步运动补偿法”将误差的“空变部分”和“非空变部分”分开补偿,“逐距离单元补偿法”的误差补偿与距离压缩同时进行,兼顾了“时不变”误差与“时变”误差的空变性,同时大大减小了剩余误差对后续成像步骤的影响。相较于一般的距离向分块补偿,它有以下优势:第一,一般的“分块补偿”其本质是“单步运动补偿法”或“两步运动补偿法”在具体应用上的改进,在第一步运动补偿后,信号中仍有一些残余误差,会影响后续的成像,而“逐距离单元补偿法”不存在此问题;第二,使用“逐距离单元补偿法”补偿后,由于所成图像场景整体误差被更好地校正,在进行后续自聚焦处理时剩余误差能被更好地估计出来。
对于频率变标(Frequency scaling,FS)算法这类首先进行方位向FT 的成像算法,补偿时仍先使用“逐距离单元补偿法”,得到补偿后的距离压缩图像,再进行距离向逆傅里叶变换,得到补偿后的回波信号。
5 仿真实验
下面通过一组仿真试验来验证上述分析的正确性。成像算法采用RD 算法,参数设置表1所示。
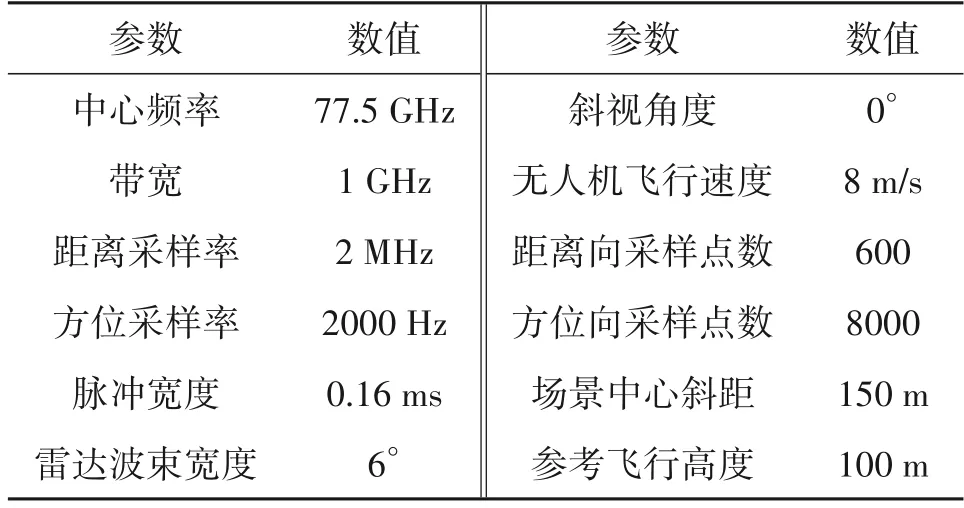
表1 仿真参数Tab.1 Simulation parameters
无人机在Y、Z轴上的初速度为0,加速度如下:
无人机的加速度、速度以及坐标变化如图5所示。
忽略雷达波束宽度带来的误差在方位向上空变的问题,各距离单元对应的Δr(tm)与ς(tm)如图6所示。
其中斜距为134 m 处与斜距为166 m 处的Δr(tm)与ς(tm)如图7所示。
从图中可见无论是Δr(tm)还是ς(tm),在各时刻均展现出了在距离向上的空变性。
场景中均匀放置了5×3的点阵作为目标。无误差成像结果、有运动误差而未补偿的成像结果如图8所示。
分别使用“两步运动补偿法”、“单步运动补偿法”和“逐距离单元补偿法”补偿后RCMC 前的二位频域如图9所示。
三种补偿方法中,“两步运动补偿法”RCMC 前的二维频域有明显误差,“单步运动补偿法”RCMC前的二维频域在距离向边缘处有轻微模糊,“逐距离单元补偿法”RCMC 前的二维频域无明显误差。成像结果对比如图10所示,其中位于点阵左上角的一个目标以及全场景中心上的目标被放大进行对比:
图11 是取三种补偿算法补偿后成像结果的方位向剖面图。
使用三种补偿方法补偿后,图11中方位剖面图对应的峰值旁瓣比(PSLR)以及主瓣的3 dB 宽度(ρa)如表2所示。
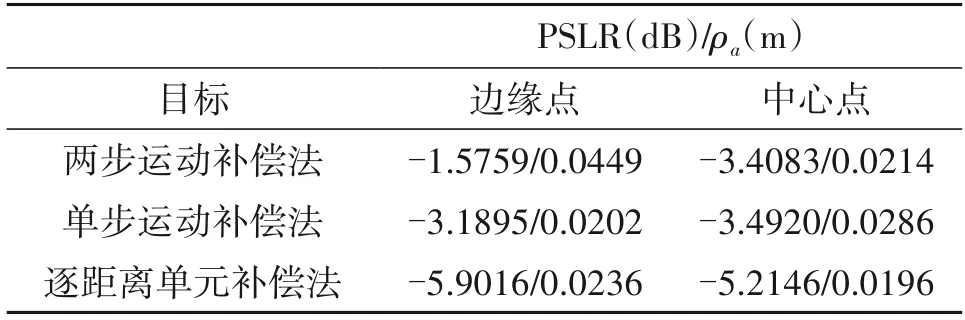
表2 各算法补偿后目标方位向上的PSLR和ρaTab.2 The PSLR and ρa of the target in azimuth direction after compensation by each algorithm
由于误差设置较大,使用“两步运动补偿法”或“单步运动补偿法”补偿后目标的成像结果仍散焦严重,且出现严重畸变,目标在方位向上的主瓣出现严重展宽,这两个问题在靠近成像场景边缘的目标上尤为严重;而使用“逐距离单元补偿法”补偿后,虽并未完全校正误差,但无论是对于靠近成像场景边缘的目标还是场景中心目标,均能有较好的成像效果。
使用各补偿算法补偿后成像结果的熵如表3所示。由于多旋翼无人机所搭载的雷达方位向波束可能较宽,在其他仿真参数不变的前提下,雷达方位向波束宽度为8°和12°的情景也被仿真。

表3 各算法补偿后成像的图像熵Tab.3 Entropy of the image after compensation by each algorithm
一般来说,熵越小,图像聚焦效果越好。从图像熵来看“,逐距离单元补偿法”具有最高的补偿精度。
综上,在正侧视的成像模式下,“逐距离单元补偿法”在补偿的精度方面要优于另外两种补偿算法。
6 结论
本文提出了一种“逐距离单元补偿法”。在不考虑方位向空变误差的前提下,该算法在距离压缩步骤将误差几乎全部校正,相较于“两步运动补偿法”以及其改进算法——“单步运动补偿法”,补偿精度进一步提升。在基于运动参数补偿时,新的补偿算法改善了靠近场景边缘的点的补偿,这对于多旋翼无人机载SAR 这类易产生较大的随距离空变误差的SAR来说较为重要。
一般而言基于IMU 的补偿并不能完全去除运动误差带来的影响,还需要自聚焦去除剩余误差。然而自聚焦去除剩余误差的能力有限,完全依靠自聚焦进行运动补偿并不可取,所以提高基于IMU 数据的补偿的精度第一有利于直接提高最终成像质量,第二便于后续高精度的误差估计,故本文提出的“逐距离单元补偿法”对于多旋翼无人机载SAR高分辨率成像而言具有重要意义。

