基于认知无人机移动中继网络的物理层安全通信研究

曹胜男 贾向东，2 郭艺轩 牛春雨 万妮妮

（1.西北师范大学计算机科学与工程学院，甘肃兰州 730070；2.南京邮电大学江苏省无线通信重点实验室，江苏南京 210003）

1 引言

第五代移动通信和下一代网络技术的快速发展，使频谱需求急剧增长，无线频谱资源愈加稀缺，认知无线电（Cognitive Radio，CR）已被广泛认为是一种提升无线频谱利用率的有效方法［1］。除CR 技术外，中继协同（Relay Cooperation，RC）传输是另一种提升无线通信系统性能的方法［2］。中继协同的无线通信可以改善链路质量和可靠性以及增加网络覆盖范围等［3］。因此，将CR和RC技术结合起来，构成的认知-中继协同（CR-RC）通信系统可以提升无线电频谱资源的利用率［4］。此外，由于无线信道的开放性，无线网络的安全通信是当下研究热点。

近年来，无人机（Unmanned Aerial Vehicle，UAV）凭借其高机动性、按需部署和视距链路（Line of Sight，LoS）等特性给无线通信带来了广阔的发展前景，但UAV 涉及的物理层安全通信系统面临着挑战［5］。文献［6］研究了UAV 作为协同干扰机，通过发送干扰信号来提高系统的安全性能。文献［7］考虑当地面存在潜在窃听者时，UAV 向合法接收者发送机密信息，通过优化UAV 的轨迹来提高系统的保密率。文献［8］研究了UAV 充当基站时的系统保密率，但并未考虑UAV 通信系统的频谱资源紧缺问题。文献［9］研究了UAV 作为次用户发射机来辅助认知无线电网络（Cognitive Radio Network，CRN）的物理层安全问题。由于建筑物和其他障碍物的阻塞，无线通信面临着困难，因此，文献［10］研究了一个两跳无线中继网络的安全通信问题。提出了一种中继辅助的通信方案来提高无线通信的质量。文献［11］研究了多中继网络协同干扰技术，提出了一种联合功率分配和中继选择方案。但传统的静态中继缺乏灵活性和扩展性，而UAV 中继可以方便部署和灵活应用，调整其位置以适应环境的变化，从而显著提高系统性能［12］。文献［13］研究了UAV移动中继系统通过优化轨迹来提高系统的安全性能，但UAV 的发射功率是固定的。文献［14］研究了UAV 的轨迹设计和功率分配问题，以最大限度地提高中继网络的保密率。但采用块坐标下降法解决问题，可能导致较高的迭代复杂度。文献［15］提出了UAV 中继网络下的联合优化方案，但并没有考虑到有潜在窃听者威胁下的安全问题，并且采用的放大转发中继策略，在进行信息传输时噪声也会被扩大。

综上，结合UAV 中继和CRN 的相关研究文献较少，因此本文提出了一种UAV 辅助中继网络的方案，该方案中部署UAV 作为认知中继，以辅助次用户发射机和次用户接收机之间的信号传输。在源节点、UAV 中继节点发射功率和UAV 飞行轨迹约束条件下，设计了一个联合优化UAV 飞行轨迹和发射功率方案，同时在满足主接收机处给定的干扰阈值下使保密率最大化。由于目标函数是非凸函数，一般难以求解。本文提出了一种基于逐次优化方法的高效迭代凸逼近算法来解决所提出的非凸优化问题，即一个较低计算复杂度的内近似（Inner Approximation，IA）算法［16］。该算法可优化一系列的凸逼近程序，也可优化非线性程序。仿真结果表明，该方法在UAV 不同飞行速度和窃听者不同位置情况下均可行，同时较传统的直线轨迹和静态中继策略，可以有效地提高UAV通信系统的保密率。

2 系统模型

本文研究了一种认知UAV 辅助的解码转发中继窃听信道模型。如图1 所示，该网络由一个认知UAV 中继（Cognitive Relay，CR）、一个次用户发射机（Secondary Transmitter，ST）、一个次用户接收机（Secondary Receiver，SR）、一个窃听者（Eavesdropper，Eve）和一个主用户接收机（Primary Receive，PR）构成，其中每个节点均配备一个天线，所有配备一个天线的节点在半双工模式下工作。假设UAV有一个较大的缓冲区，并作为一个移动中继从ST接收数据，并利用解码转发中继策略将其转发到SR，Eve 采用被动窃听的方式对UAV 进行窃听。假设地面节点ST 和SR、Eve、PR 之间的通信链路被阻断，本文通过UAV 移动中继建立良好的空对地信道，将机密信息发送给其他目的终端。假设UAV 已知合法用户位置并可通过其配备的光学相机或合成孔径雷达来检测和跟踪潜在Eve的位置［17］。地面节 点ST、SR、Eve 和PR 的坐标分别为(0，0，0)，(xSR，ySR，0)，(xEve，yEve，0)，(xPR，yPR，0)。

随着UAV的移动，UAV与各终端节点之间的距离不断变化，各通信链路的信道状况也随之变化。由于UAV 轨迹的连续性，所考虑的优化问题涉及无穷多变量，使得问题难以解决。为简化问题，将UAV的飞行周期T离散为N个等长的时隙，即T=Nδt，其中δt表示基本时隙长度，当每个时隙足够小时，可以假设UAV 在每个时隙内的飞行速度是恒定的，不考虑加速或减速。因此，UAV 在时隙n的时变坐标表示为预先确定UAV 的初始位置q0(x0，y0，H)和最终位置qF(xF，yF，H)。UAV 的最大飞行速度是Vmax，则每个时隙UAV 最大飞行距离为Dmax=Vmaxδt。此外，为了航空安全，UAV 高度限制在H以内。因此，UAV信道约束条件如下：

假设UAV 与地面节点之间空对地信道为LoS链路通信，不同链路之间相互独立且互不干扰。并且由于UAV 移动性所引起的多普勒效应可以被完美的补偿。则在时隙n时ST 到UAV、UAV 到各地面节点SR、Eve、PR 的信道功率增益记为hx，x∈{SU，UR，UE，UP}遵循自由空间路径损耗模型，因此用自由空间路径损耗表示为：

其中ρ0为参考距离d0=1 m 时的信道功率增益，为UAV与地面节点之间的距离。xS[n]，xU[n]分别表示为ST 到UAV 和UAV 到各终端节点的时隙n处的传输信号分别表示为ST和UAV在时隙n时的信号发射功率。同时需要满足平均功率-P和峰值功率Pmax的约束：

考虑UAV 采用的是解码转发中继来辅助通信，故该系统模型分为两个阶段。第一阶段，ST发送信号xS[n]给所有终端节点，由于高山或建筑物的阻挡，存在严重的衰落和阴影问题，ST 与其他终端节点之间没有直连链路，所以ST 发送信息给UAV 中继节点。第二阶段，UAV 中继将从ST 接收到的信号解码转发给其他地面节点。

因此，在UAV处接收到的时隙n时的信号为：

在时隙n处，从ST到UAV的链路传输速率为：

在SR、PR、Eve 处接收到UAV 的时隙n处的信号分别为：

相应链路的瞬时传输速率分别表示为：

此外，还考虑了从UAV 到PR 的干扰链路。在某个时隙n，UAV-PR信道上的干扰功率为：

同时还需要考虑PR 处的平均干扰阈值约束，以保护通信。约束（13）确保PR 处的平均累积干扰功率必须小于给定的阈值ε，ε＞0。

其中，zj[n]～CN(0，σ2)，j∈{SU，SR，Eve，PR}表示加性高斯白噪声。本文在不失一般性的情况下，假设所有节点接收到的噪声功率是相同的且为1。

因此，该CRN的平均保密率可以定义为：

3 优化问题

本文目标是通过联合优化UAV 的飞行轨迹q={x[n]，y[n]}和发射功率p=PS[n]，PU[n]，满 足UAV 中继的移动性约束、发射功率约束、PR 处的平均干扰功率约束，使次用户通信系统的保密率最大化，将CR-RC网络的平均保密率问题表述为：

问题P 是难以求解的，因为它对于p，q的目标函数是非凹性的。即P 是一个非凸规划问题，不能直接用标准凸优化技术求解。为了简化问题P，首先将式（15）转化为另一个非凸且更易于处理的形式，然后提出一种基于IA 方法的迭代算法来求解。为使（15）易于处理，推导了P 的目标函数保密率值的一个下界，利用ln(1 +ex)的凸性和Jensen 不等式，又由log函数性质得RS[n]的下界为：

令Xn=PU[n]hUS，λn其中Xn是指数分布的随机变量，k是欧拉常数。利用下式［18］：

将式（18）代入式（17）中，得RS[n]的凹下界：

由于函数ln(1 +x)的凹性，REve[n]的凸上界：

利用式（19）和式（20），问题P 可以近似转化为下式：

3.1 提出的联合优化方案

本节应用较低计算复杂度的IA 方法求解问题P1。引入新的松弛变量r≜{rS[n]，rEve[n]}，n∈N来重写式（21），如下所示：

目标函数（22）是一个线性函数。因此需处理非凸约束条件（23）、（24）和（13）。

凸规划约束条件（23）：为简化问题，引入新的松弛变量zU[n]和tS[n]得：

约束条件（25）～（27）在最佳状态下保持相等。用log2(1 +tS[n])的一阶近似，在迭代算法的第k次迭代时，即点处来近似式（25），利用公式得：

根据二次函数关于变量x，y(x＞0，y＞0) 的一阶泰勒展开式［20］：

得到点(x(k)[n]，y(k)[n])附近，式（27）的一阶近似值，迭代地将其替换为以下线性约束：

凸规划约束条件（24）：引入新的松弛变量zEve[n]和tEve[n]将式（24）等价地表示为：

由于log2(1 +tEve[n])是一个凹函数，因此非凸性约束条件（32）可以近似表示为：

最后，引入新变量zPU[n]，约束条件（13）可以等价地替换为：

同理，约束条件（13）可重写为：

式（39）是一个凸约束条件，其中zPU2[n]在定义域(2zPU[n]-zPU(k)[n]) ＞0时的下界为：zPU2[n](2zPU[n]-zPU(k)[n])。

类似地，约束条件（38）可以近似为：

综上，P2可重新表述为一个更易解决的问题：

约束条件（42）是凸二次型约束和线性约束条件，可以用IA算法有效地求解。

4 仿真及数值结果分析

本节将通过仿真验证所提出的联合优化移动中继飞行轨迹和发射功率方案的安全性能。考虑在不同UAV 飞行速度影响下的平均保密率，以及不同Eve位置影响下的UAV飞行轨迹与平均保密率。同时与传统的静态中继和无优化方案进行比较。假设所有的通信节点均置于三维直角坐标系中，ST、SR和PR 的三维坐标分别设为(0，0，0)，(500，500，0)和(800，-800，0)。Eve分别取三个不同的位置(200，-500，0)，(500，-500，0)，(800，-500，0)。假设UAV在固定高度H的平面以速度Vmax∈(20，25，30)从起始位置(-200，200，200)单向飞行到终止位置(800，200，200)。

图2 描绘了当UAV 飞行速度为30 m/s 时，不同时间段的飞行轨迹和直线轨迹。首先，将地面节点位置以及UAV 的初始和最终位置坐标在图中标出。其次，可以看到随着时间T的增加，UAV 会飞近SR，悬停在SR 附近传输机密信息，并逐渐远离Eve。最后，经过多次迭代，特别是当T=150 s时，UAV达到该时刻的最优飞行路径。可见直线轨迹并非最优路径，并且随着时间T的增加，UAV轨迹逐渐收敛。证明所提联合设计方案能够有效改善通信链路，提高次用户系统的安全保密率。

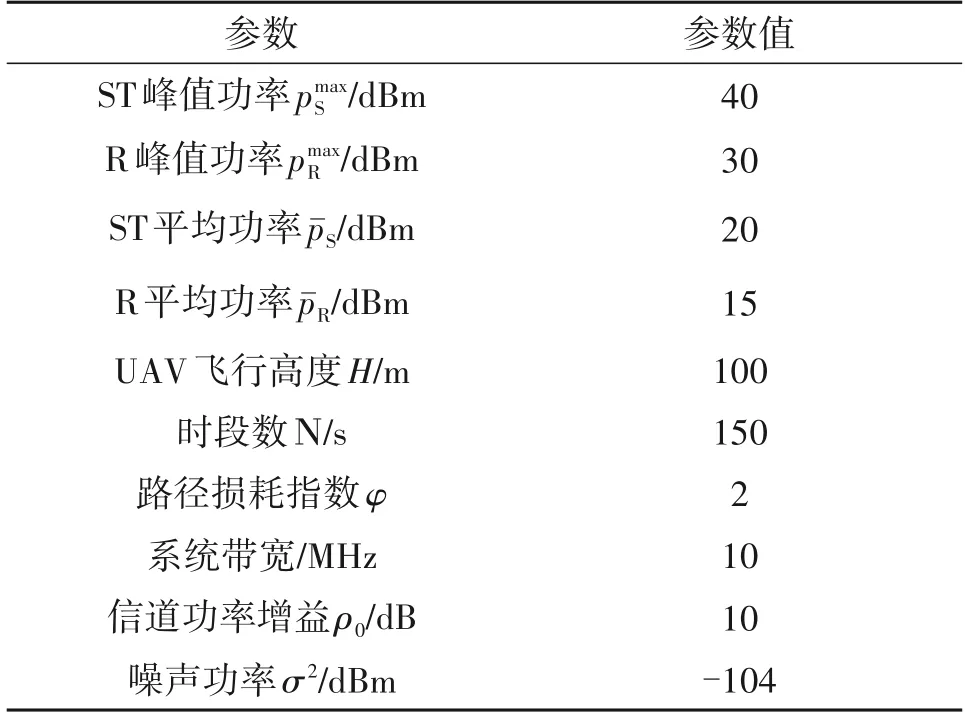
表1 仿真参数Tab.1 Simulation parameters

图3给出了联合优化方案中，不同飞行速度下的次用户系统的平均保密率。可见UAV移动中继系统的平均保密率会随着其飞行时间的增加而增加，并且飞行速度越大，平均保密率越高，收敛程度也越快。当总飞行时间超过80 s时，各条曲线平均保密率逐渐趋于稳定。因此，可以将饱和点用作最小总飞行时间，以保证最佳平均保密率性能。

图4 描绘了当飞行速度为20 m/s 时，不同Eve位置下，所提联合优化方案的UAV 最优飞行轨迹。如图是当T=150 s 时，三个不同位置的Eve 最终迭代后的飞行轨迹。Eve 位置不同，UAV 最终飞行轨迹不同。这是由于随着Eve 位置变化，UAV 轨迹趋势会发生相应的变化，即及时调整位置来反窃听。当UAV 悬停在ST 或SR 上方时，能够得到最佳的接收或传输链路。并且较大的速度和飞行时间，可以获得更多在ST 或SR 上空的悬停时间，以此来提高飞行性能和保密性能。

图5 比较了当UAV 飞行速度为25 m/s 时，传统静态中继方案、无优化方案和本文所提联合优化方案的平均保密率。联合优化方案平均保密率收敛于3.3，无优化和静态中继分别收敛于0.85 和1.6。显然所提出的联合优化方案在保密性能方面优于静态中继方案和无优化方案。这也证明了联合优化UAV 飞行轨迹和功率方案可以有效提高系统的平均保密率。

5 结论

本文研究了一种UAV 辅助的认知中继网络安全通信问题，提出了一种保密率最大化的联合优化方案。由于在PR 的干扰功率与ST 和UAV 的发射功率约束下所考虑的问题是非凸的，很难得到有效的解决。因此采用一种基于连续凸逼近的求解算法来优化问题，使得近似凸规划的问题得到最优解。仿真结果证明了联合优化方案在最大化CR-RC 网络的平均保密率问题的优越性。同时，这项工作可以扩展到认知用户物理层安全性能等方面的研究。