基于蒙特卡洛模拟计算连通率不同方法比较研究

兰志广 徐 源 聂细江 郭 猛 王海宇

（天津市勘察设计院集团有限公司，天津 300191）

0 引言

结构面连通率是综合描述岩体内部结构面发育尺寸及贯通程度的重要指标，在评价岩体的强度及稳定性等方面都发挥着积极作用[1]。因此，国内外学者针对连通率的计算方法进行了许多有益探讨与研究。总体来看，根据计算结构面连通率所需数据来源（实测或者模拟）不同，连通率计算方法可分为两大类，即基于实测的概率模型估算法和基于蒙特卡洛模拟计算法[2]。如黄建安[3]从结构面组合的几何关系出发研究计算了连通率；黄润秋等[4]通过结构面全迹长调查估算了连通率；黄国明等[5]在实测结构面平均迹长以及岩桥平均长度的基础上推导了H-H 连通率估算公式；汪小刚等[6]基于蒙特卡洛模拟考虑结构面与岩桥相互作用的破坏机理并运用动态规划原理计算了连通率；陈剑平等[7]基于蒙特卡洛模拟运用理想截面投影法计算了连通率；李启源[8]基于H-H 连通率估算公式提出了EHH 法估算了连通率；Zhang 等[9]基于蒙特卡洛模拟运用最短路径法计算了连通率。

基于实测的概率模型估算法估算连通率时，需要追踪调查结构面沿走向方向的延伸情况或者调查统计特定尺寸窗口范围内所有结构面。由于现场结构面往往隐伏于地表之下，即使出露其规模尺寸也有限，因此，现场结构面调查难度较大，耗时耗力。相较而言，基于蒙特卡洛模拟计算法，仅依靠有限露头面上调查所得结构面，通过蒙特卡洛模拟生成结构面网络模型即可计算获得连通率。因此，考虑到工程实践的经济性，基于蒙特卡洛模拟计算法计算连通率更有优势。本文具体介绍了三种基于蒙特卡洛模拟计算连通率的方法，并通过举例对比分析了不同方法结果的差异性，为以后工程实践提供理论指导。

1 方法介绍

基于蒙特卡洛模拟计算法计算连通率的基本思路是，调查有限露头面上结构面数据并利用蒙特卡洛模拟生成结构面网络，然后以模拟所得结构面网络为数据依据计算连通率。由于结构面网络模拟可分为二维结构面网络模拟和三维结构面网络模拟，相应的，基于蒙特卡洛模拟计算法可分为二维连通率计算方法和三维连通率计算方法。本文主要针对二维连通率计算方法进行比较研究。目前，基于蒙特卡洛模拟计算二维连通率的方法可归纳为三大类，分别是带宽投影法、动态规划法以及最短路径法，介绍如下：

1.1 带宽投影法

带宽投影法是一种比较传统的计算连通率的方法，其基本思路是：根据工程实际在结构面网络中布置特定方向的测量基线并设定带宽，然后向该测量基线投影设定带宽范围内所有的结构面迹线（见图1），连通率则可通过计算测量基线上投影所得结构面迹长的总和与测量基线长度的比值获得[10]，计算公式为：

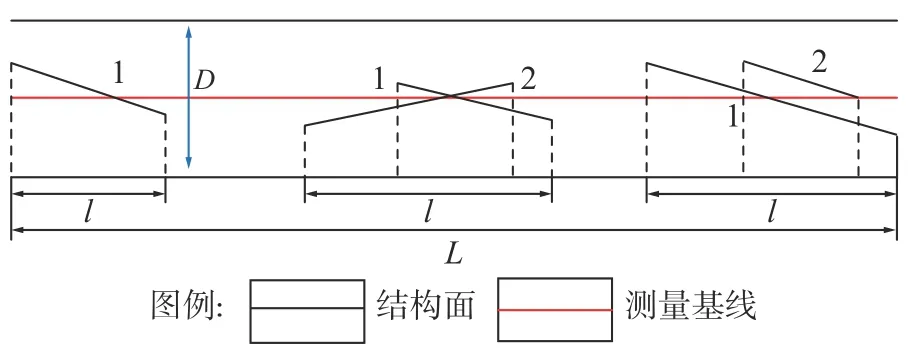
图1 带宽投影法简图

式中：L为测量基线的长度；D为带宽；n为结构面迹线的条数；θ 为结构面迹线与测量基线的夹角。

带宽投影法的优点是计算简单快捷，但其值的可靠度严重依赖于带宽的取值。文献[11]研究表明，随着带宽增加，采用带宽投影法计算所得连通率值会相应增加直至100%。因此，合理选择带宽是保证带宽投影法可靠度的重中之重，而目前为止，带宽的取值尚没有统一定论，多依赖于在实际调查基础上进行经验分析取值[2]。

1.2 动态规划法

动态规划法将连通率由几何意义拓展到力学意义，其基本思路是：考虑结构面与岩桥相互作用的破坏机理，并运用动态规划原理在结构面网络中搜索沿特定方向且具有最小抗剪强度的结构面-岩桥组合而成的潜在破坏路径，这条潜在破坏路径上结构面迹长总和与潜在破坏路径长度的比值即为连通率[6]，即：

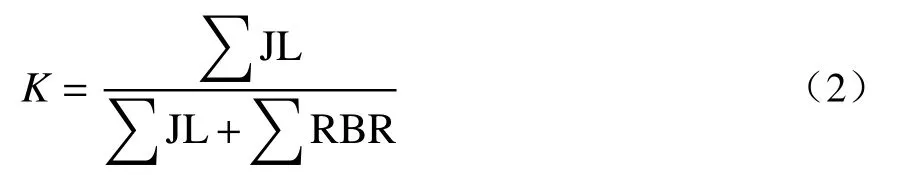
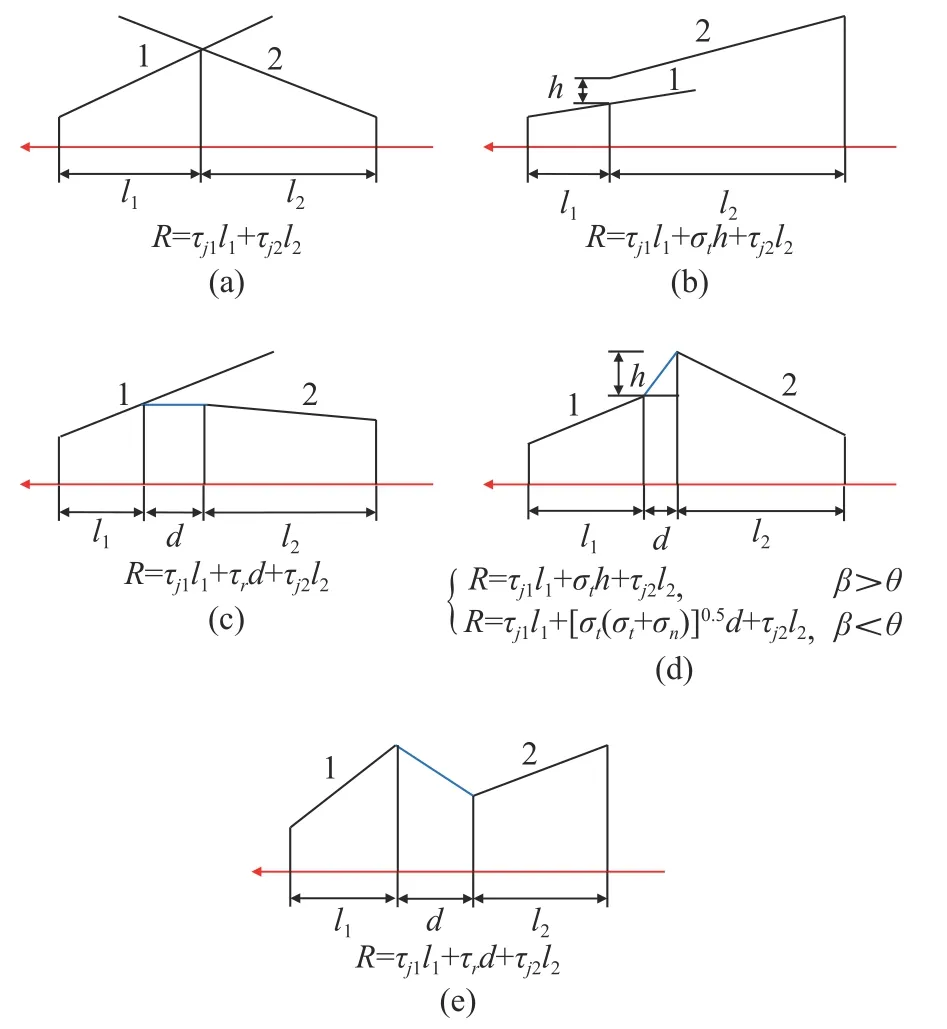
图2 结构面与岩桥相互作用破坏机理

动态规划法考虑了岩体破坏时结构面与岩桥之间相互作用的破坏机制，所得连通率值更具有理论价值和实际意义。文献[11]研究表明，动态规划法所得连通率值与带宽、模拟剖面尺寸以及正应力有关：在一定范围内，连通率值会随带宽增大而增大，当带宽增大到一定程度后，连通率会趋于稳定；模拟剖面尺寸对连通率值的影响规律同带宽一致；正应力取值对连通率值有一定影响，且在低应力条件下，这种影响更明显。

1.3 最短路径法

最短路径法与动态规划法思想类似，也是以结构面网络上搜索沿特定方向的潜在破坏路径为目的，然后以潜在破坏路径上结构面迹长总和与潜在破坏路径长度的比值作为连通率，即：

区别于动态规划法，最短路径法搜索潜在破坏路径时并没有考虑结构面与岩桥相互作用的破坏机理。但其合理性在于：由于结构面的力学强度较完整岩石小几个数量级，在岩体破坏时，往往有沿结构面滑动的趋势。而岩体破坏路径经过的结构面越多，其抗滑力就越小。假设完整岩石之间两点的距离为d，相同距离的结构面迹线中的两点距离为d′，可视d′ ＜＜d。这样，在限定潜在破坏路径的入口与出口时，潜在破坏路径的总长度越小，经过的结构面迹长就越大，潜在破坏路径最短时，则最大可能的经过了岩体中的结构面，沿此路径破坏时所受的抗剪力最小[13]。因此，岩体潜在破坏路径可视为沿入口与出口之间的最短路径。

目前，最短路径法常用到的算法有Dijkstra 算法以及Floyd 算法。本文采用Floyd 算法，算法介绍见文献[14]。以图3所示节点为例，应用Floyd 算法计算节点a 与节点d 之间的最短路径，通过更新矩阵D和矩阵P，可得到a→d 之间的最短路径为a→c→d，最短距离为3+1=4。

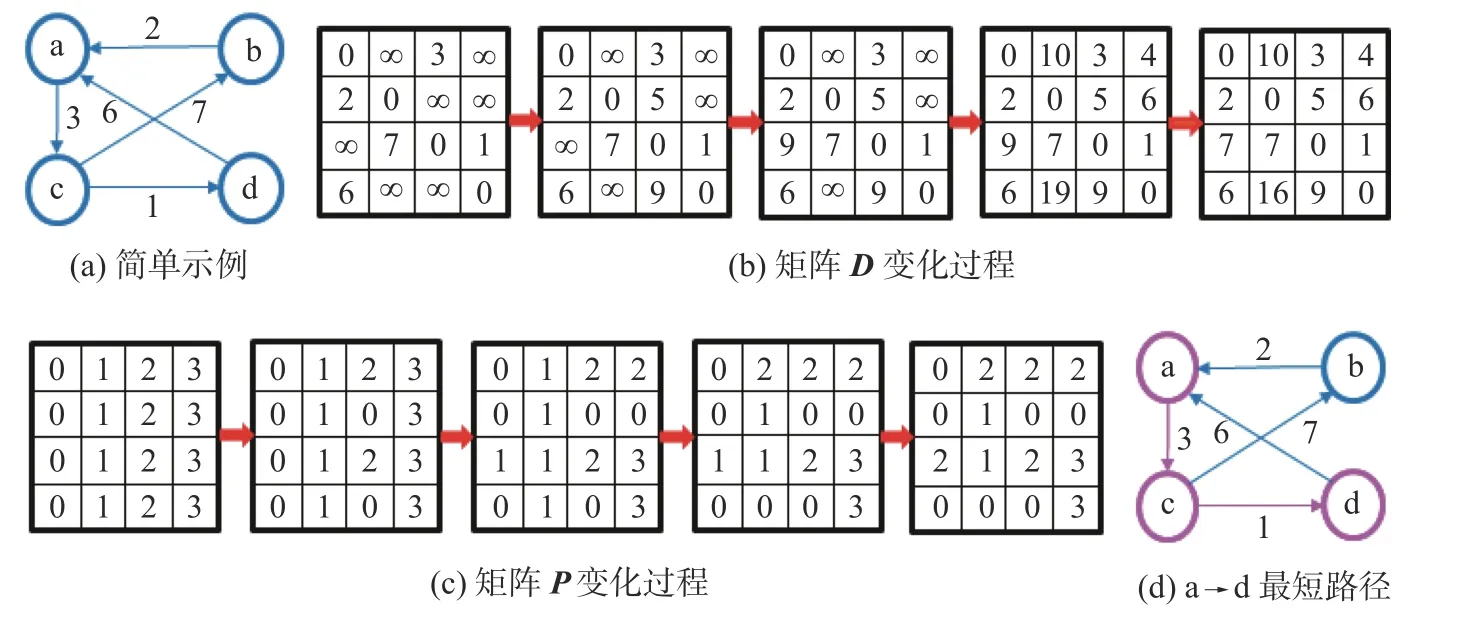
图3 Floyd 算法计算最短路径示例

最短路径法计算思想简单，但值得注意的是，最短路径算法针对节点进行搜索，故在实际搜索时，需将结构面网络中的结构面迹线进行离散化。文献[9,13,14]研究表明，结构面迹线离散化程度越高，搜索结果越精确，但计算量也越大；此外，对于指定不同搜索方向，最短路径法计算所得连通率值也不相同，体现了岩体结构的各向异性。

2 举例计算

2.1 举例模型

某一水平岩体表面随机发育有大量结构面，统计分析其几何参数，采用蒙特卡洛模拟生成一个尺寸为100 m (X轴) × 100 m (Y轴) × 100 m (Z轴)的三维结构面网络模型，关键步骤如下[1,14,15]：

（a）结构面产状模拟：采用基于施密特下半球等面积投影网的概率统计法对各组结构面产状频率进行校正[16]，校正公式见式（4）：

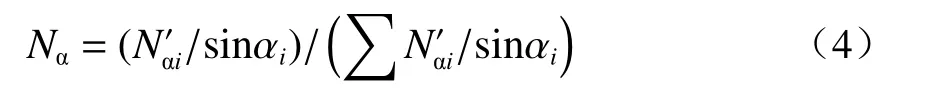
式中：Nα为结构面产状频率的校正值；α为结构面的平均倾角；Nα

′为观测频率。

（b）结构面尺寸模拟：基于结构面形状为圆盘的假设，结构面尺寸可由结构面圆盘直径来表征，且结构面圆盘直径与迹长存在空间理论关系[16]：

式中：ch为出露半迹长；r为圆盘半径。

（c）结构面密度模拟：采用张量法[17]来计算用于三维结构面网络模拟的裂隙密度。具体计算公式见式（6）：

2)为结构面直径平方的均值。

（d）蒙特卡洛模拟：通过上述步骤确定的结构面几何参数（见表1），利用MATLAB 自编代码采用蒙特卡洛模拟法，即可生成一个尺寸为100 m (X轴) ×100 m (Y轴) × 100 m (Z轴)的三维结构面网络模型（见图4）。

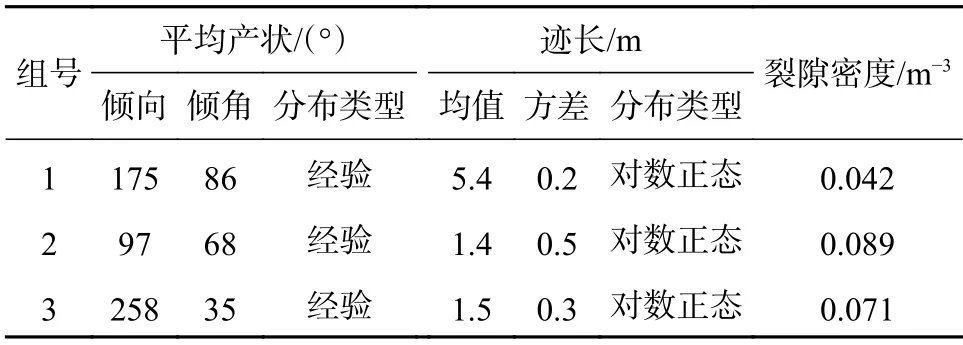
表1 结构面主要几何参数统计

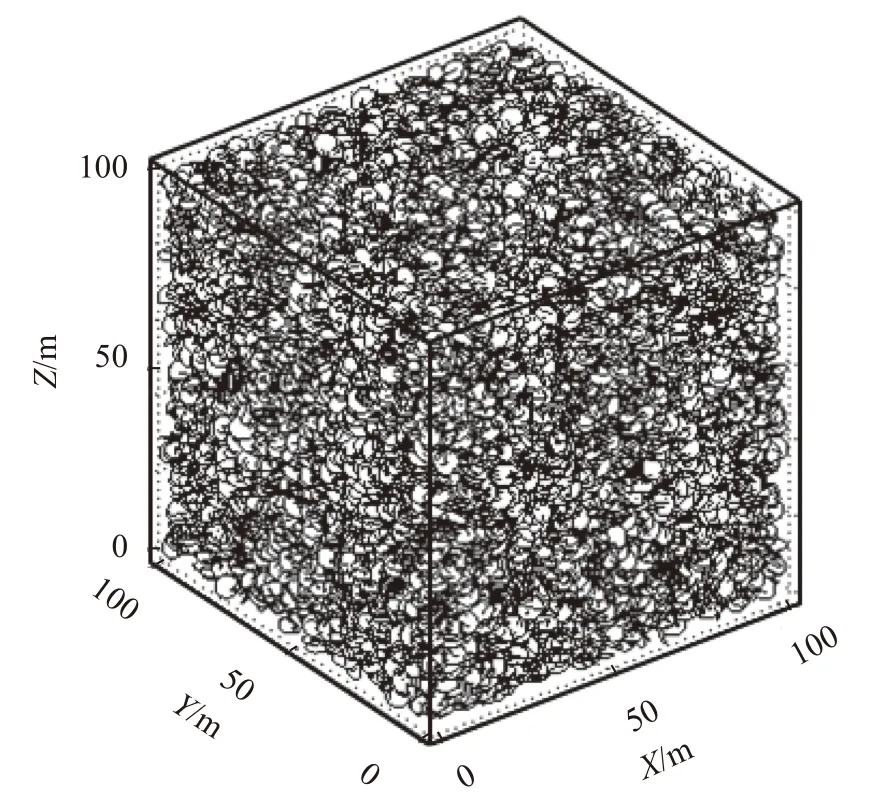
图4 三维结构面网络模型

选择某剖面与三维结构面网络模型相截切，即可得到该剖面上的二维结构面网络[1]。本文以走向为30°，且过三维结构面网络模型体心的剖面为例，模拟所得结构面网络见图5。

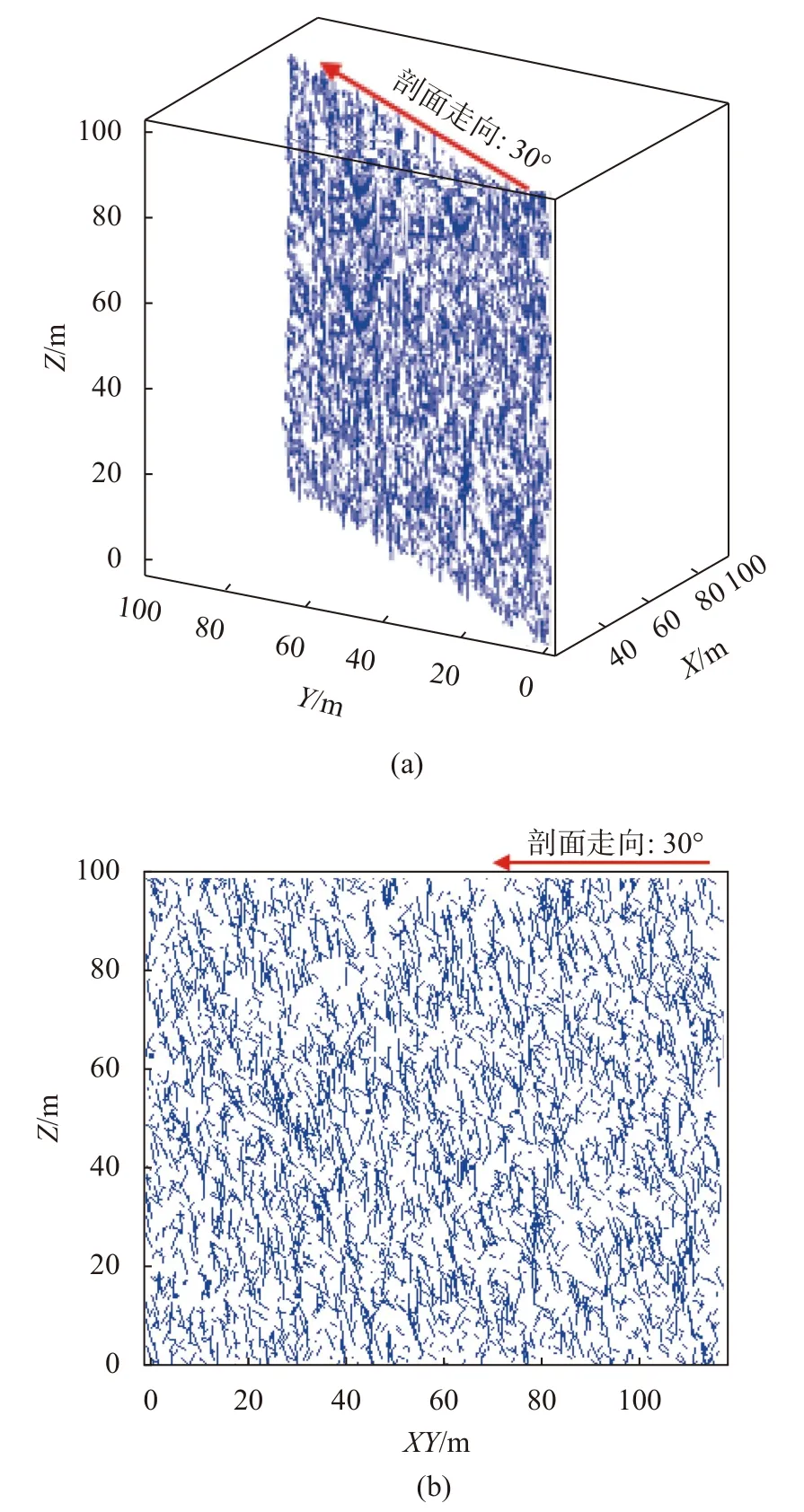
图5 二维结构面网络模拟图

2.2 带宽投影法计算

采用带宽投影法计算连通率时，本文考虑影响计算结果的因素有投影基线方向和带宽。在与二维结构面网络XY轴夹角为10°～180°的方向上每隔10°布置一条测量基线（见图6），分别计算其带宽为1～15 m（间隔1 m）时的连通率，计算结果见图7。

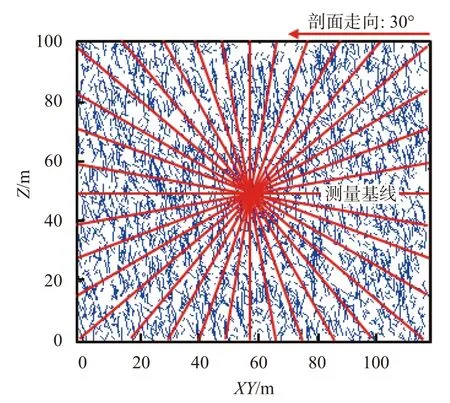
图6 测量基线布置图

由图7可以看出，不同投影基线方向计算所得连通率值是不同的，以投影带宽1 m 为例，投影基线10°时连通率值最小，为19.97%；投影基线100°时连通率值最大，为46.09%。对比不同投影带宽时连通率计算结果，虽然不同投影基线方向计算所得连通率值没有明显变化规律，但整体而言，均是在投影基线100°附近连通率值达到最大。此外，投影带宽对连通率值的影响较为明显，变化规律较为明确，随着投影带宽的增大，连通率值也相应增加，以投影基线10°为例，随着投影带宽由1 m 增大到15 m，连通率值也由19.97%增大到83.34%。而在投影基线100°、投影带宽15 m 时，连通率值最大，为96.53%。

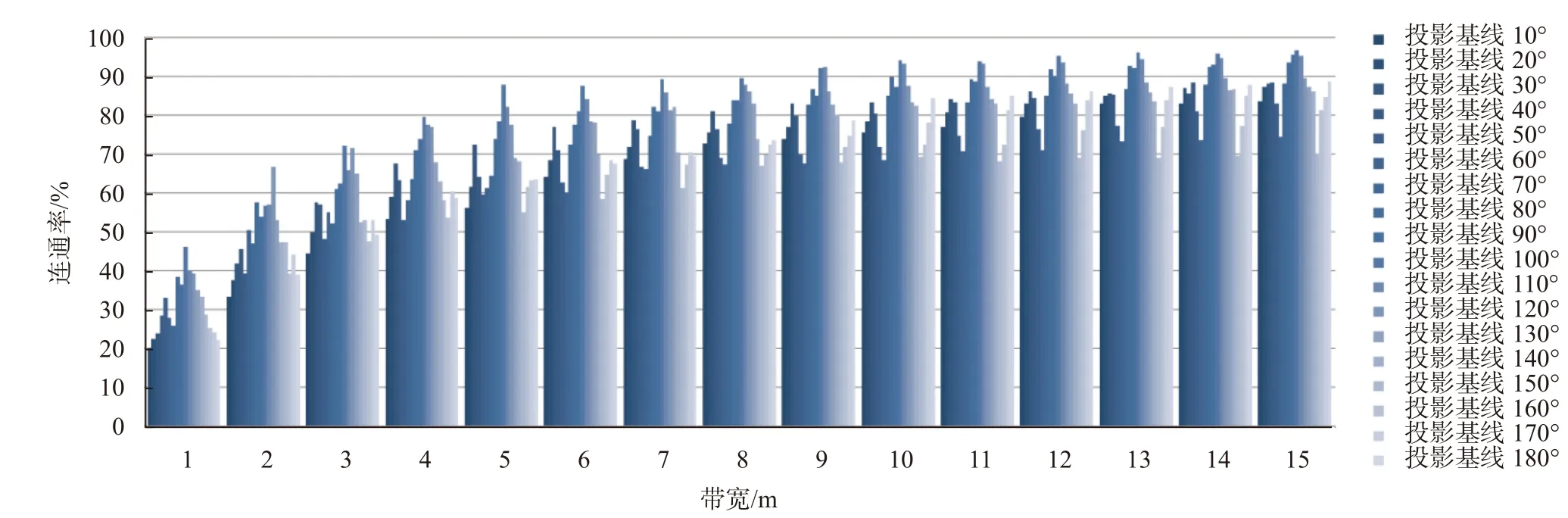
图7 带宽投影法计算结果统计图

2.3 动态规划法计算

采用动态规划法计算连通率时，本文考虑影响计算结果的因素有剪切方向和带宽，正应力对连通率值的影响暂不做考虑。假定岩体摩擦系数为0.95、黏聚力为0.85 MPa，结构面摩擦系数为0.5、黏聚力为0.15 MPa，在与二维结构面网络XY轴夹角为10°～180°的方向上每隔10°布置一个剪切方向（见图6），分别计算其带宽为1～15 m（间隔1 m）时，正应力为3 MPa 时的连通率，计算结果见图8。

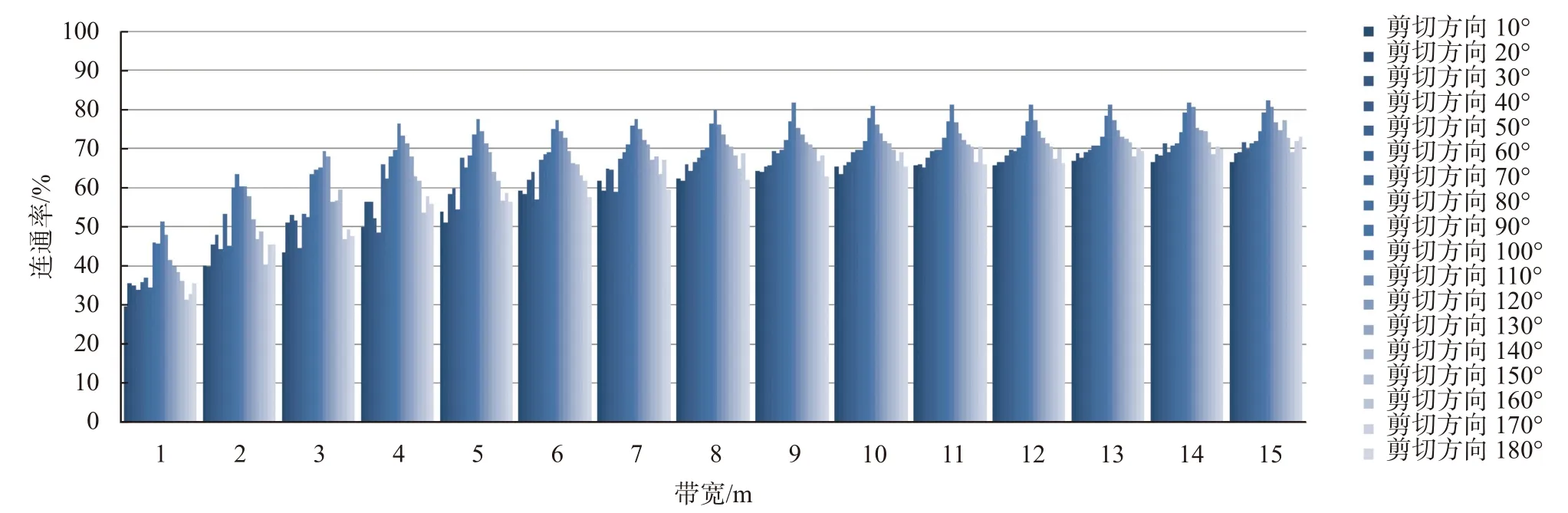
图8 动态规划法计算结果统计图

由图8可以看出，不同剪切方向计算所得连通率值也是不同的，以带宽1m 为例，剪切方向10°时连通率值最小，为29.61%；剪切方向100°时连通率值最大，为51.45%。对比不同带宽时连通率计算结果，不同剪切方向计算所得连通率值除在剪切方向100°附近连通率值达到最大外，也没有其他明显变化规律。此外，带宽对连通率值的影响较为明显，变化规律较为明确，在一定范围内，随着带宽的增大，连通率值相应增加，但当带宽增大到一定值后，连通率值趋于稳定，以剪切方向10°为例，在带宽1～9 m，连通率值由29.61%增大到64.41%，在带宽9 m 之后，连通率值在65.59%与66.49%之间波动。

2.4 最短路径法计算

采用最短路径法计算连通率时，本文考虑影响计算结果的因素有路径搜索方向和带宽，结构面迹线离散化程度暂不做考虑。在与二维结构面网络XY轴夹角为10°～180°的方向上每隔10°布置一个搜索路径方向（见图6），分别计算其带宽为1～15 m（间隔1 m）时，迹线离散为6 个点时的连通率。计算结果见图9。

由图9可以看出，不同搜索方向计算所得连通率值也是不同的，以带宽1 m 为例，搜索方向10°时连通率值最小，为30.27%；搜索方向100°时连通率值最大，为50.77%。对比不同带宽时连通率计算结果，不同搜索方向计算所得连通率值除在搜索方向100°附近连通率值达到最大外，也没有其他明显变化规律。此外，同动态规划法一样，带宽对连通率值的影响较为明显，变化规律较为明确，在一定范围内，随着带宽的增大，连通率值相应增加，但当带宽增大到一定值后，连通率值趋于稳定，以搜索方向10°为例，在带宽1～9 m，连通率值由30.27%增大到64.04%，在带宽9 m 之后，连通率值在65.22%与66.70%波动。

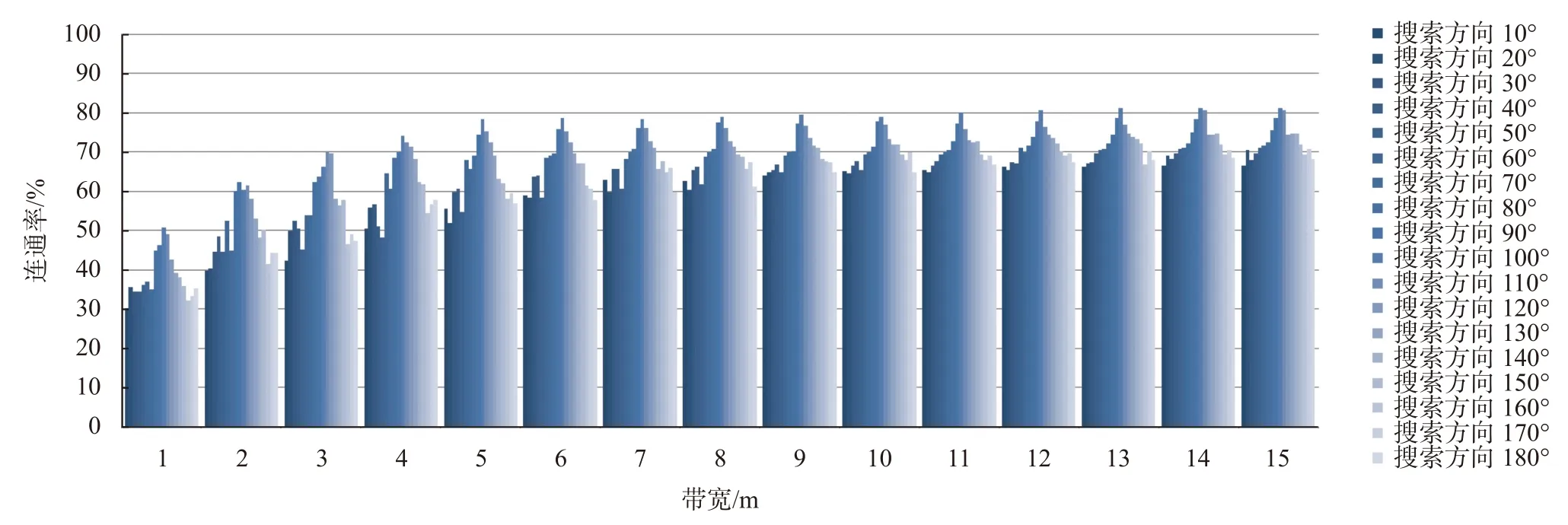
图9 最短路径法计算结果统计图

3 计算结果对比分析

分析对比上述三种计算方法所得连通率结果，可以发现三种计算方法结果均受限于投影基线（或剪切、或搜索）方向和带宽的选择。其中，投影基线（或剪切、或搜索）方向对连通率值的影响规律尚不明确，但从三种方法计算所得连通率值的结果来看，不同投影基线（或剪切、或搜索）方向计算所得连通率值不同，说明三种方法计算所得连通率值均是呈现各向异性的；在不同带宽时，三种方法均是在投影基线（或剪切、或搜索）方向100°时连通率值达到最大，说明这三种方法在寻找连通率值最大（即岩体最容易发生破坏）方向是一致的。

对比带宽对三种计算方法所得连通率值的结果（见图10），可以明显看出，在不同投影基线（或剪切、或搜索）方向时，带宽投影法计算所得连通率值会随着带宽的增大持续增大，而动态规划法和最短路径法计算所得连通率值均是在带宽增大达到一定程度后趋于稳定；此外，动态规划法和最短路径法计算所得连通率值在不同带宽时均较为一致，而带宽投影法计算所得连通率值只有在带宽2～3 m 范围内与其他两种方法保持一致。

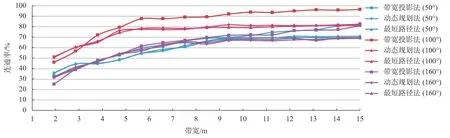
图10 不同方法计算结果对比图（以基线/剪切/搜索方向50°、100°、160°为例）

综上分析，认为在工程实践中需求一个经济安全的连通率值时，带宽投影法由于其不能提供一个稳定的值，显然是不合适的；相较而言，动态规划法和最短路径法能满足要求。但是比较动态规划法和最短路径法，动态规划法需要明确岩体和结构面强度参数及其所受正应力，在初始条件不足时，动态规划法应用也将受限，因此，本文推荐使用最短路径法。在工程实践中，建议采用最短路径法首先粗略计算不同搜索方向连通率值，待确定最大连通率值所在方向后，重点计算该方向不同带宽时的连通率值，并以趋于稳定后的不同带宽连通率平均值作为连通率建议值。如本文案例在带宽5 m 之后连通率值于78.38%～81.15%波动，建议取带宽5～15 m 连通率均值，即79.75%作为连通率建议值。

4 结论

本文通过举例分析对比带宽投影法、动态规划法以及最短路径法计算所得连通率结果，得到如下结论：

（1）就寻找最大连通率值所在方向，带宽投影法、动态规划法及最短路径法结果较为一致，且三种方法计算所得连通率值均表现为各向异性。

（2）投影基线（或剪切、或搜索）方向一定，带宽投影法计算所得连通率值会随着带宽的增大持续增大，而动态规划法和最短路径法计算所得连通率值均是在带宽增大达到一定程度后趋于稳定；且动态规划法和最短路径法计算所得连通率值在不同带宽时均较为一致。

（3）综合分析考虑，建议在工程实践中采用最短路径法，首先粗略计算不同搜索方向连通率值，待确定最大连通率值所在方向后，重点计算该方向不同带宽时的连通率值，并以趋于稳定后的不同带宽连通率平均值作为连通率建议值。