长桩基础偏位时单桩承载力分析与讨论
杨晗琦 蔡德昌
(1.中国能源建设集团湖南省电力设计研究院有限公司,湖南长沙 410007;2.湖南省轻纺设计院有限公司,湖南长沙 410007)
0 引言
桩基础具有承载力大、施工简便等优点,在我国工程建设实践中,广泛应用于工业、民用与交通工程。
结构设计中,桩基础一般按轴心受压(上部结构传导到桩身的弯矩和水平剪力均较小)进行设计。而实际施工时,对于钻孔灌注桩,可能由于轴线定位不准、钻机钻进偏差、钢筋笼倾斜等诸多原因,造成桩的实际位置与设计定位存在偏离;而对于预应力混凝土管桩和钢桩,由于桩机移位、倾斜及沉降不均也可能造成单桩偏位[1]和断裂。
我国规范给出了桩偏位的允许值,一般不大于100 mm,实际工程中可能遇到的偏位情况处理有一定的困难,全部补桩不够经济,凭工程师个人经验处理难以推广。
近年来,国内外学者基于线弹性地基反力法对水平荷载作用下单桩的响应进行了大量研究,可分为单参数法[2]、双参数法[3]和三参数法[4],目前常用的为单参数法,其假定地基反力系数为深度的幂函数,包括常数法、M 法和C 值法,其中常数法可以推导出桩身响应的解析解[5];采用M 法假定,王伯惠等[6]推导出水平荷载作用下桩的变形和内力的幂级数解,王 哲和龚晓南[7]推导出考虑轴向荷载影响的桩身变形和内力的幂级数解,目前我国使用较多,且国家规范也采用M 法。戴自航等[8]在水平梯形分布荷载桩的桩身变形和内力分析中应用双参数法推导出了差分解。但双参数法低估了上部土体的反作用力,当地基为黏性土或基岩时计算结果与现场测量值相差较大。在此基础上吴恒立提出了三参数法,可以比较精确地考虑上部土体的反作用力,但其未能给出桩身响应的解析解。张 磊等[4]采用三参数法对水平荷载作用下的桩身挠曲线方程提出了半解析解。
运用布里渊光时域反射技术(BOTDR)的光纤应变传感技术具有诸多优点,在测试桩身内力位移时可实现分布式测量、长距离测试以及方便植入,在国内国际均已有较多应用,魏广庆等[9]采用该技术对复杂地质条件场地的两种不同工艺类型的灌注桩进行了内力测试,发现施工质量较好的T8 桩在埋深17.5 m以下就基本无桩身位移。杨建平等[10]利用基于BOTDR 分布式光纤传感技术的检测方法研究了桩基础在水平荷载作用下的桩身位移和桩身反力的分布情况,与理论方法推导结果较为吻合,说明采用理论方法对桩在水平荷载作用下的极限承载力进行估算是较为准确的。
桩在水平荷载作用下的极限水平承载力取决于桩身尺寸、材料强度和土层地质情况,桩身尺寸、材料强度决定了桩身极限弯矩值(水平荷载在桩身上产生一个弯矩,并在一定深度存在最大值),土层反力可减小桩身所受到的水平剪力从而减小桩身弯矩,同时桩侧移变形的大小直接决定了桩是否合格,即使桩身并未因水平荷载所致弯矩而折断。
桩在大偏位情况下也会在桩身上产生一个最大弯矩,且桩身在偏位荷载作用下的侧移决定了桩是否合格,因此,可以参考利用水平荷载作用下桩身极限承载力的研究成果,对桩在上部荷载作用下的极限偏位值进行估算。
本文通过对规范中单桩水平承载力的规定,结合国内外学者对单桩水平承载力的相关研究,利用地基反力系数M 法的研究成果,给出单桩在大偏位情况下的极限偏位值的计算方法。
1 长桩基础偏位承载力分析
《建筑地基基础工程施工质量验收规范》(GB 50202-2002)第5.1.4 条[11],给出了钻孔灌注桩的桩位偏差允许值(见表1),其对预制桩和钢桩也具有参考价值,可见目前规范对于桩孔位置的施工要求较高。
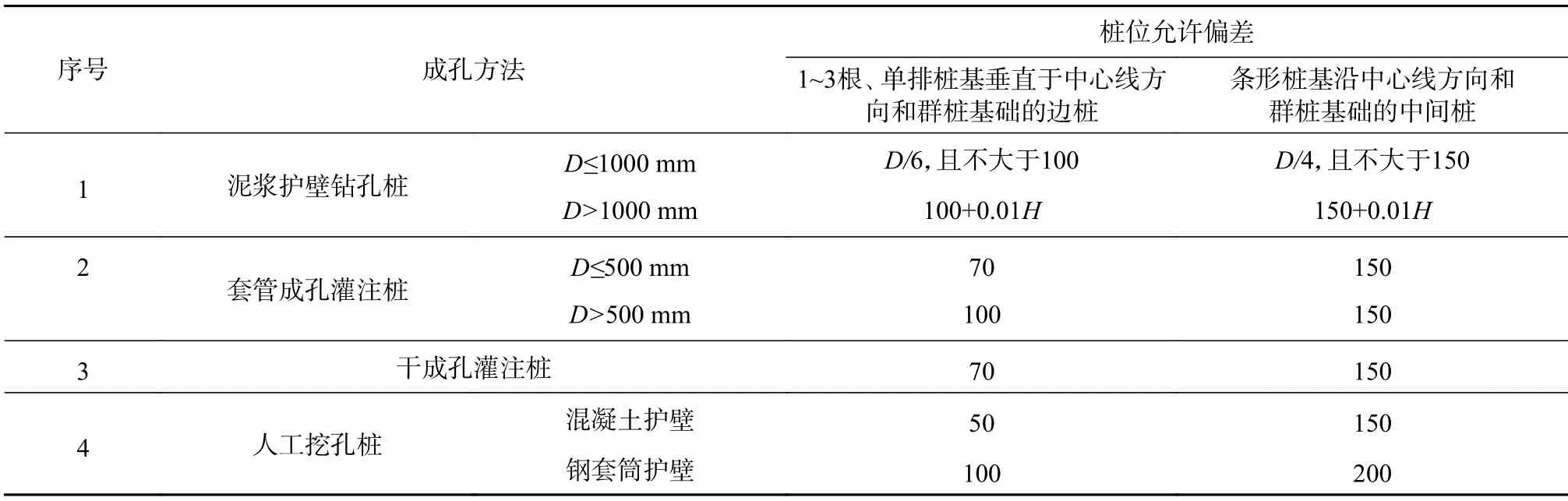
表1 灌注桩的平面位置和垂直度的允许偏差
1.1 桩的水平承载力计算
由 《建筑桩基技术规范》(JGJ 94-2008)[12]第5.7.2 条可知:对于长钻孔灌注桩,根据其桩身配筋率是否小于0.65%,其水平承载力特征值按不同类别计算。其中,对于桩身配筋率小于0.65%的灌注桩基础,由于桩身的配筋率过小,桩顶水平力较大时会导致桩身开裂,此时灌注桩的单桩水平承载力特征值由桩身强度控制(即按裂缝控制)[12];而对于桩身配筋率不小于0.65%的灌注桩基础,其单桩水平承载力特征值取决于桩顶的允许水平位移值(桩身断裂前桩顶位移已大于规范允许值:桩基规范规定可根据静载试验结果取地面处水平位移为10 mm 所对应的荷载的75%为单桩水平承载力特征值,其中对于水平位移敏感的建筑物取水平位移6 mm)。因此本文将把长钻孔灌注桩按桩身配筋率是否小于0.65%分为两类来对其偏位承载力进行讨论。
第一类,桩身配筋率小于0.65%的灌注桩。《建筑桩基技术规范》(JGJ 94-2008)规定在缺少单桩水平静载实验资料时,桩身配筋率小于0.65%的灌注桩单桩水平承载力特征值可按式(1)计算:
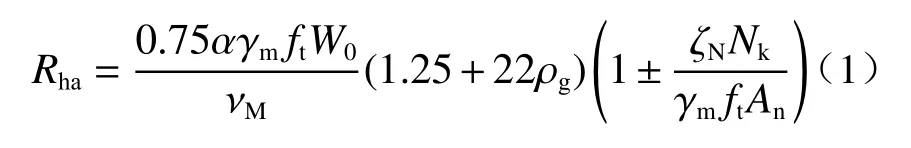
式中:α为桩的水平变形系数;Rha为单桩水平承载力特征值;γm为桩截面模量塑性系数,圆形截面取2,矩形截面取1.75;ft为桩身混凝土抗拉强度设计值;W0为桩身换算截面受拉边缘的截面模量;νM为桩身最大弯矩系数;ρg为桩身配筋率;An为桩身换算面积;ζN为桩顶竖向力影响系数;Nk为在荷载效应标准组合下桩顶的竖向力。各参数的取值和计算见《建筑桩基技术规范》(JGJ 94-2008)5.7.2 条。
第二类,桩身配筋率不小于0.65%的灌注桩。根据文献[13]的试验数据可知,对于延性较差的PHC 管桩,当桩顶水平位移小于20 mm 时,桩身所承受的弯矩小于开裂弯矩,而当桩顶水平位移大于20 mm,桩身最大弯矩随桩顶水平位移的增加而急剧增加,可见,对于配筋率不小于0.65%的灌注桩,规范选用的水平位移限值是很保守的。预制桩、钢桩和桩身配筋率不小于0.65%的灌注桩可根据静载实验结果取地面处水平位移为10 mm 所对应的荷载的75%为单桩水平承载力特征值,其中对于水平位移敏感的建筑物取水平位移6 mm。当缺少静载试验资料时,按式(2)进行计算[12]:

式中:νx为桩顶水平位移系数;EI 为桩身抗弯刚度;χ0a为桩顶允许水平位移。
1.2 桩偏位时偏位限值的计算
由表1可知,规范对于桩偏位的允许值较小,而对于三桩以上群桩基础的桩孔偏位,规范允许偏差较为宽松,且对于单根桩设计承载力有富余的群桩承台,实际设计中还可以通过核对各桩承担轴力的大小,并调整承台配筋来使群桩基础满足设计要求,如校核发现单桩轴向承载力仍不满足要求,则需要加桩。但对于单桩基础的任意方向及两桩基础垂直桩中心线方向,轴力较大时,大偏位情况下由于桩偏位导致轴力偏位所产生的弯矩也较大,该弯矩将无法由桩本身来进行平衡,必须由桩侧土反力来进行平衡。
目前对桩孔偏位的处理方法有纠偏、补桩等,但对于桩身配筋率不大于0.65%的构造配筋桩基础,纠偏时易发生桩身断裂,而实际工程中,如果大偏位的桩基础数量较大,全部补桩处理,不仅费用高昂,也耽误工期,因此如果能够结合桩侧土的反力来进行考虑,根据场地、桩长、桩身配筋率、成桩方式等因素进行综合评价,判定各单桩基础需进行补桩的极限偏位值,具有一定的实用价值和经济效益。
本文对单桩基础及两桩基础的讨论范围限定在:
①桩发生较大偏位,但桩身倾斜度不大于规范允许值。
②桩为长桩基础,其换算埋深αh大于4.0,其中α为桩的水平变形系数,h为桩长。
桩基础顶部所受荷载通常为轴向力N、弯矩M和水平荷载H,同时受到地基的水平抗力p(z)=b1σ(x),在这些荷载作用下发生挠曲,假定桩的水平承载力由位移控制,即桩身处于弹性状态,由文献[14]可知,桩弹性挠曲微分方程为
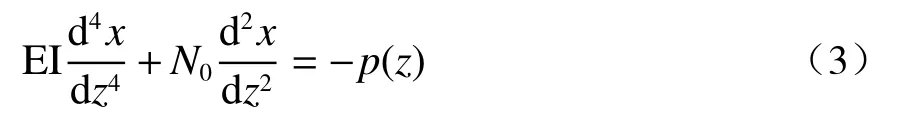
式中:EI 为桩身弹性模量;N0为轴力。
由于桩在水平方向的允许位移很小,根据《建筑桩基技术规范》(JGJ 94-2008)第5.7.2 条2 款[12]可知,对于预制桩、钢桩以及配筋率不小于0.65%的灌注桩的水平位移限值为10 mm,对于水平位移敏感的建筑物取水平位移为6 mm,因此,单桩基础无偏心情况下,由于轴力N所产生的弯矩增加值M1较小,弯矩增加值M1不大于轴力的1/100,可不考虑轴力N的影响。
化简得到桩的挠曲微分方程为
(1)健全信用体系。第一,完善行业信用记录,利用大数据进一步优化信用数据库。同时,健全负面信息披露制度和守信激励制度,逐步建设和完善以组织机构代码和身份证号码等为基础的实名制信息共享平台体系;第二,加快信贷征信体系建设,建立金融业统一征信平台;第三,培育信用服务市场,提高全社会的信用意识,树立良好的社会信用风尚。

式中:α为桩的水平变形系数。
杨建平等[10]对受水平荷载的桩进行了分布式检测和数值模拟,发现水平变形主要集中在地面与桩深6 m 的范围内,随着水平荷载的增大,桩身弯矩呈非线性增大,且最大弯矩点也向更深处转移。这与《建筑桩基技术规范》(JGJ 94-2008)表5.7.2[12]的规定是相符的,其认为当桩的换算埋深αh大于4.0 m后,桩顶水平位移系数νx和最大弯矩系数νM与αh等于4.0 m 相同,张 磊等[4]也指出了桩长较长时,桩底的边界条件对桩的响应影响较小,故本文认为桩深h>4.0/α的部分对变形及受力无影响。
采用幂级数对式(4)求解可得到桩身各位置的内力及位移的简捷表达式:

式中:Ax、Bx、Aφ、Bφ、AM、BM等为参数,数值见表2。

表2 内力及位移参数取值表[7]
对于桩身配筋率不小于0.65%的灌注桩和预制桩、钢桩(第一类桩),其水平承载力由位移控制,最关键的控制值为桩顶最大位移Xzmax,而对于由桩身强度控制的配筋率不大于0.65%的灌注桩(第二类桩),其最关键的控制值则为桩身最大弯矩Mzmax,《建筑桩基技术规范》(JGJ 94-2008)计算出的桩的水平承载力H1max未考虑桩轴力的偏心以及弯矩,可以假定此时桩顶侧向位移仅由水平力控制(即轴力无偏心,桩顶无弯矩)。
对于由位移控制的桩(第一类桩),不考虑桩顶弯矩和轴力产生的附加弯矩的情况下,当仅在相当于水平承载力特征值大小的水平荷载作用下时,由表2可知其桩身最大水平位移发生在桩顶,为:

式中:Ax1为αh=0 位置处的Ax值;H1max为单桩的水平承载力特征值。
由表2可知,桩偏心时在荷载作用下桩身产生的最大位移发生在桩顶,为:

M2max为柱端传来的弯矩M2与柱偏心导致的最大弯矩M2p的矢量和,H2和M2max可能不在一个平面上,其各自产生的位移需经变换到一个平面上。
已知,桩由位移控制,两种情况下最大允许位移应该相等,令xz1=xz2,则有

由式(9)和式(10)可推导得

允许极限偏位值为

对桩身配筋率小于0.65%的灌注桩(第二类桩),在仅受水平荷载作用下时(不考虑轴向力的附加弯矩和柱顶弯矩)其桩身最大弯矩为
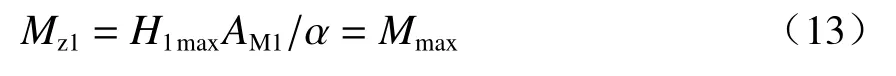
式中:AM1为桩身上所取到的AM的最大值。
在偏心荷载及桩端水平力作用下,其桩身最大弯矩为
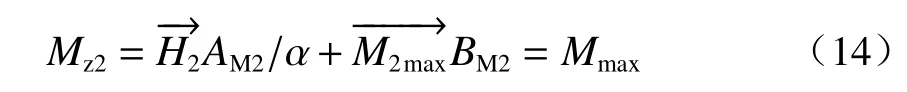
式中:AM2、BM2为桩身上Mz2最大处的AM、BM值。对于偏心荷载作用下的桩身最大弯矩,不一定在桩顶处,仅在水平荷载为0 的特殊情形下才是。
由式(13)和式(14)可推导得到:
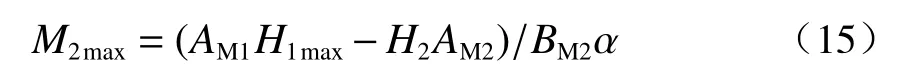
允许极限偏位值为:

2 实例计算
以湘潭某钢结构厂房桩基础施工为例,采用干作业钻孔灌注桩,D=700 mm,桩身配筋10 根直径14 mm 纵筋,两桩间距为2.1 m,由于在测量时发生一些失误,以及钻机钻进时定位不够准确,导致A 轴线两桩基础发生较大偏位,以10 轴、15 轴、20 轴及25 轴交A 轴承台各桩为例,具体偏位见表3。场地土分层情况为:素填土①,褐红色夹灰色黏性土,结构松散,稍湿-湿,层厚0.6~14.5 m;粉质黏土②,褐黄-褐红色高岭土,硬塑状为主,稍湿,层厚1.3~7.0 m;粉质黏土③,褐黄色,见灰白色团状高岭土及黑色铁锰氧化物,可塑,韧性中等,稍湿-湿,层厚1.1~6.8 m;圆砾④,褐黄色,呈亚圆形,石英硅质碎屑为主,粒径大于2 mm 占65%左右,中密,稍湿-湿,层厚2.9~6.8 m;强风化粉砂质泥岩⑤,紫红色,粉砂泥质
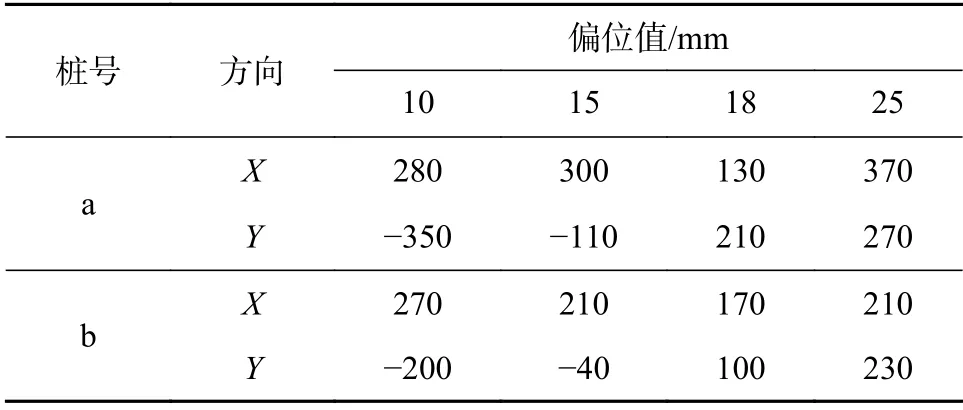
表3 桩偏位数据
结构,层状构造,岩石风化严重,遇水易软化,致密,稍湿,层厚3.5~6.7 m;具体参数见表4,原地勘资料中,未给出素填土①的压缩模量,经过现场查勘,发现大部分区域素填土较为密实,故认为其可承受一定水平压力,假定其压缩模量为3 MPa。桩身配筋率为0.4%,柱脚传来荷载标准值为轴力N=1414 kN,Y向弯矩为M=-464 kN·m,Y向水平力H=-85.5 kN·m,按1.2 节中第二类桩的水平承载力进行计算,各桩的轴压力按《建筑桩基技术规范》(JGJ 94-2008)第5.1.1 条进行计算,对于桩身仅需考虑垂直于桩连线方向的桩偏心所带来的弯矩,计算得到水平抗力系数α为0.4617,故影响深度H=4.0/α=8.66 m,与文献[10]检测结果一致。

表4 场地土层参数
由此可得到各桩的X向水平承载力、极限弯矩值及极限偏位值见表5。
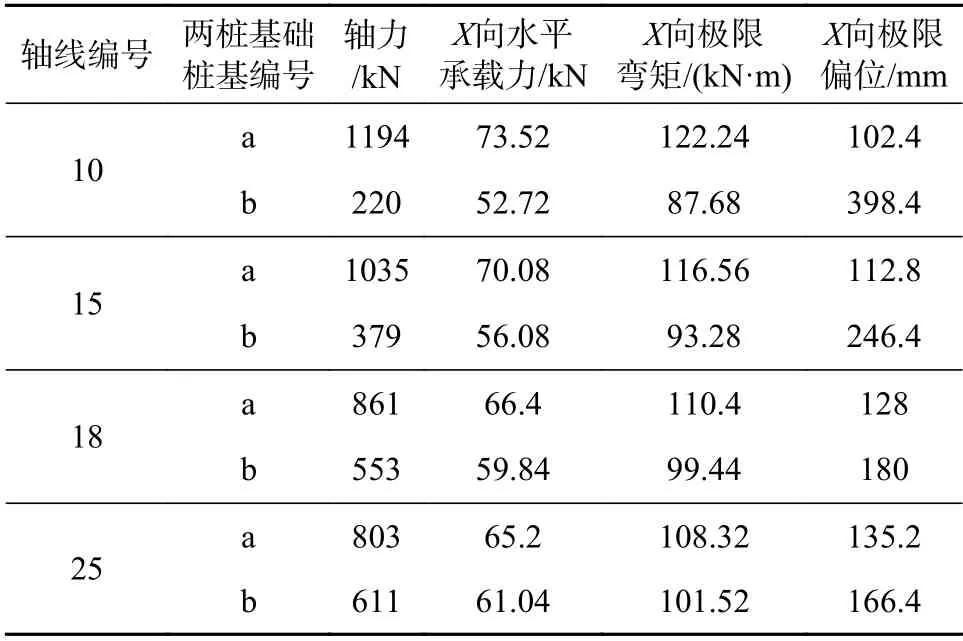
表5 桩各参数极限值
钻孔灌注桩的成桩工艺系数为0.7~0.8,本算例取0.75,计算得到其桩身承载力为4125 kN。其极限偏位值与桩身轴压比的关系曲线见图1。

图1 轴压比–极限偏位值关系曲线(桩身强度控制)
假设桩身配筋率不小于0.65%,即当为高配筋率桩时,根据《建筑桩基技术规范》(JGJ 94-2008)第5.7.2 条第2 款,取允许桩顶水平位移为10 mm,按2.2 小节第二类计算水平承载力,再按式(15)计算极限弯矩与偏位值如表6,其极限偏位值与桩身轴压比的关系曲线见图2。

表6 桩各参数极限值
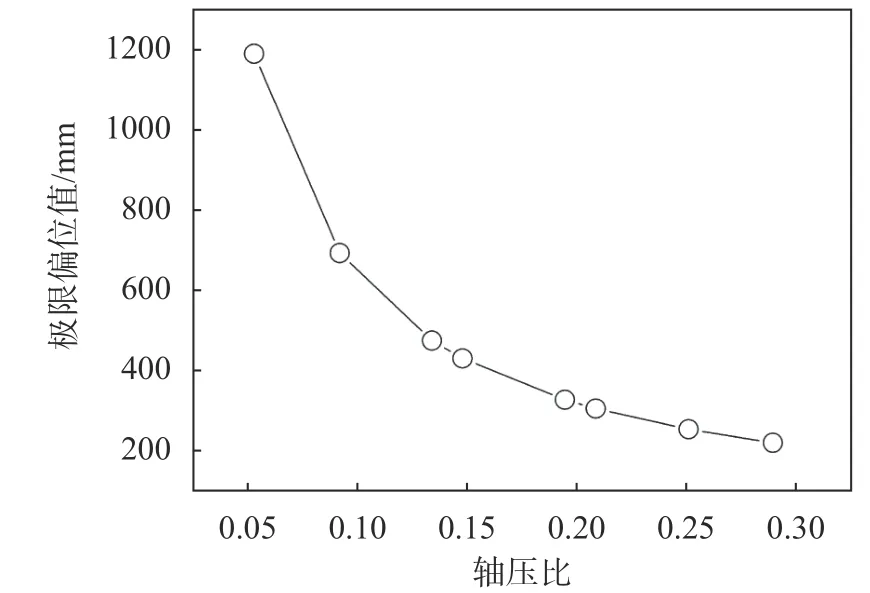
图2 轴压比–极限偏位值关系曲线(位移限值控制)
3 讨论
由表5可知,对于配筋率小于0.65%的钻孔灌注桩,其水平承载力与桩所受的轴向压力有关,轴压力越大,其水平承载力越高,从受力角度分析,这是由于轴压力延缓了受拉侧混凝土的开裂与发展,同时,轴压力越大,相同偏位值的弯矩也越大,由计算结果可知极限偏位值为102~398 mm,此结果较符合《建筑地基基础工程施工质量验收规范》对于桩偏位值不得大于100 mm 的规定,同时,桩轴压比越大,极限偏位值越小,且随轴压比增大而快速下降,在轴压比0.2 左右即接近规范允许值,因此对于地基土质较差的长桩基础,桩的极限偏位值需严格遵守。同济大学设计院对上海某软弱土层单桩基础的水平加载试验研究表明[15]:承受上部结构传来的竖向荷载作用的抗压桩,其试验得到的水平承载力特征值是根据规范公式计算得到的水平承载力特征值的1.4 倍,因此当上部结构传来的水平荷载不大时,经严格计算,对轴压比较小的单桩基础的偏位限值可适当放宽。
由表6可见,由位移控制的桩,其计算水平承载力在桩顶位移为10 mm 左右时较表5中的水平承载力有一定增加,这可能是周围填土承载能力较弱,计算采用的m 较小所致,而其所能承受的偏位值则达到2 倍以上(大于200 mm),可见,对于桩身承载力较高的长桩基础,如果其轴压比小于0.3,且建筑物对于桩顶水平位移不敏感,可以将极限偏位值放宽到200 mm,依靠土的抗力来进行平衡,从而减少加桩。而对于桩偏位大于计算值或者超出了桩身的情况,可以考虑在单桩顶面设连系梁来平衡弯矩,以减小桩身最大弯矩。
4 结论
本文按桩身配筋率(是否小于0.65%)能否提供足够桩身强度进行分类,分为①桩身强度控制型长桩基础和②桩顶位移控制型长桩基础。参考桩基规范中长桩基础在水平荷载作用下的承载力特征值计算公式和现有的M 法对桩在荷载作用下的桩身内力和变形分布情况,对长桩基础在偏心轴力作用下的极限偏心弯矩承载力进行了推导,得到单桩和两桩基础在两种情况下无需进行处理的最大偏心距计算公式,得到如下结论:
(1)对于桩身配筋率小于0.65%的灌注桩,其极限偏位值由桩身强度控制,计算出的极限偏位值在很小的轴压比(0.25)即接近了规范的允许偏位值,因此当其在上部荷载作用下的轴压比达到0.15 以上时,其极限偏位值即需按规范规定从严要求。
(2)对于水平承载力由位移控制的桩基础(桩身配筋率大于0.65%),由于其桩身强度较高,即使偏位较大也不会发生桩身断裂,当其轴压比小于0.3 时,其极限偏位值可放宽到200 mm。当轴压比大于0.3 时,需更多案例提供支持。
(3)上述两点提出的具体放宽限度是在大范围较厚回填土、压缩模量取值较低的给定土质情况下根据地基规范进行计算的,如土质情况较好,其极限偏位值可适度放宽。同时,对于上述两种灌注桩,如在纵横两个方向增加地基梁拉结,可以有效约束桩顶位移,减小桩身最大弯矩值,提高桩的极限偏位承载力。

