广义薄膜方程的数值求解

贺裕 付宝君 杨雨婷

（哈尔滨师范大学 黑龙江哈尔滨 150025）

近年来，由于电子控制与检测水平的迅速发展，新型制膜技术不断涌现，薄膜技术和薄膜材料也开始成为真空技术和材料科学等领域备受瞩目的重要研究领域，薄膜科学已逐渐成为一门研究薄膜生产技术、生长原理、物性分析方法与控制的科学［1］。在使用外延生长技术制备薄膜时，沉积原子会落在衬底表面上，并通过某一种方式相遇到一起，从而产生一些原子团。随着新原子的不断加入，这些原子团逐渐长大变成较大的粒子簇，人们将这种粒子簇称为“岛”。随着沉积过程的持续进行，原子岛不断生长，当原子岛长到一定阶段时，在原子岛内部相互连接，形成通道网络结构。在沉积不断进行时，原子填补通道之间的空隙，形成连续薄膜［2］。薄膜生长过程是比较复杂的原子活动，涉及沉积原子经历的各种动力学过程，包括原子间扩散的动力学过程、原子团扩散的动力学过程和多层膜生长的动力学过程。

众所周知，四阶薄膜方程可描述相变、薄膜增长等物理过程，并且都可用如下形式来描述：

其中，Ω ⊂RN为具有光滑边界∂Ω 的有界区域，T为正数，p＞1，u=u(x，t)表示薄膜表面的高度。相关文献［3］构造了方程（1）的弱解，并证明其存在唯一性。

当N=1 时，方程（1）为广义薄膜方程［4］，近年来被广泛研究。

当p=2 时，方程（1）称为Cahn-Hilliard 方程［5］，最初用于表达了分离过程中守恒浓度场的演化，如今已成为材料科学和工程的支柱。这个方程也支持在图像分析中用来提高模糊图像清晰度的方法。相关文献［6］描述了Cahn-Hilliard方程在放射性资源采集与迁移建模中的应用。

相关文献［7］提出了描述薄膜外延生长的能量守恒方程：

ut=g-∇·j+η

Zangwill 提出薄膜表面的高度函数u(x，t)满足周期边值条件和某种初值条件［8］。相关文献［9］利用Galerkin 逼近得到了弱解。King 等人利用半离散逼近思想，证明了外延薄膜生长初边值问题在适当函数空间中弱解的存在性、唯一性和正则性，同时导出解的长时间行为［10］。

本文主要研究以下初边值条件的广义薄膜方程问题：

并简要论述一些基本概念和定义，以及求解方程的时间差分、再生核样条函数法（RKSM），随后，给出了所提方法的理论分析，最后，数值算例验证了算法的有效性。

1 相关理论

定义3［11］Wm[a，b]=u(x)|u(x)(m-1)在[a，b]上绝对连续，u(x)(m)∈L2[a，b]，其内积定义为：

则，Wm[a，b]是再生核空间。

定理3[11]再生核空间Wm[a，b]的再生核函数为：

定理4[12]再生核空间Wm[a，b]的再生核函数Rm(x，y)关于变量x是2m-1阶样条。

针对此问题，构造再生核空间W5[a，b]，在此空间对方程进行讨论，并取W3[a，b]中的再生核函数作为5次样条的一部分基底，然后，运用配置法，对方程的精确解进行数值逼近，并将全面系统地对本文构造的再生核样条法进行理论分析，对数值解的一致收敛性进行严格地证明，最后给出数值算例来验证该算法的有效性。

2 再生核样条函数法的具体求解过程

证明：设存在不全为0 的数c1、c2、c3、c4、…cn+5，使得：

取pj(x) ∈W5[a，b]，满足：

且p(ji)(a)=p(ji)(b)=0，i=0，1…5；j=5。

由内积定义（3），将式（5）两边分别与pj(x)做内积，可得：

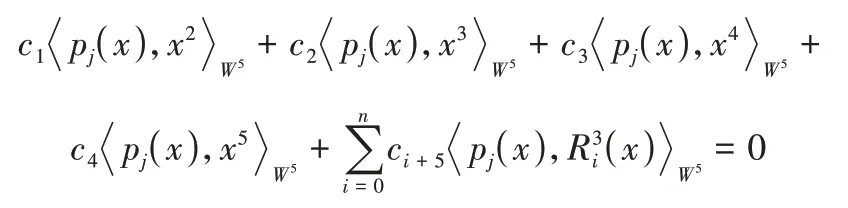
容易求得ci+5=0(i=0，1…n)，而{x2，x3，x4，x5}显然线性无关，有c1=c2=c3=c4=0。

设矩形域={(x，t)|a≤x≤b，0≤t≤T}，取空间步长h=(a=x0＜x1＜…＜xM=b)，即x=xk=a+(k=0，1，…M)；时间步长τ=(0=t0＜t1＜…＜tT=T)，即t=tn=nτ(n=0，1，…N)。其中，N，M都是正整数。用两族平行直线t=tn=nτ和x=xk=a+将矩形域进行网格剖分，网格节点记为(xk，tn)。

以下是对时间变量进行差分，格式如下：

其中，un表示第n 个时间层上的函数，即un=u(x，tn)，代入方程（1），整理得：

近似解un(x)有如下表示形式：

在配置点xk=a+(k=0，1，…，M)上进行计算，使用配置法来获取un(x)，它的系数a1、a2、…aN+5满足：

引入矩阵U=(a1，a2，…aN+5)，则式（9）、式（10）、式（11）转化成矩阵方程：

其中，C为系数矩阵，B为常数项。且C非奇异，因此，un(x)存在且唯一。

3 理论分析

定理6：设u(x，tn)是方程（2）的精确解，un(x，tn)是u(x，tn) 的近似解，则un(x，tn) 和它的各阶导数u(k)(x，tn)一致收敛于精确解u(x，tn)及其各阶导数

证明：令R(x，y)是再生核空间W5[a，b]的再生核函数。由：

有：

而再生核函数在［a，b］是连续的，因此：

|u(x，tn)-un(x，tn)|≤M‖u-un‖→0

其中，常数M=‖Rx‖≥0。

即：un(x，tn)一致收敛于u(x，tn)。

其中，常数Mk=≥0(k=1，2，3，4)。因此，各阶导数u(k)(x，tn)一致收敛于u(nk)(x，tn)。

4 数值算例

例：考虑如下广义薄膜方程的初边值问题［13］。

其中，p分别取2，3，4，5，6，其精确解u(x，t)=ex+x+(t-2)。

取M=10，N=10，xk=(k=0，1，2…，10)，tn=(n=0，1，2…，10)，用文中的方法计算的最大绝对误差和最大相对误差见表1。

表1 方程（12）中p 取不同值的最大绝对误差和相对误差