Baarda粗差探测和M抗差估计的优劣性比较

闫占瑞

（铁正检测科技有限公司 山东济南 250101）

基于均值平移模型的粗差探测是处理观测值粗差的主要方法之一［1］，它主要采用逐步搜索的方法来实现粗差的定位与定值，通常有向前、向后搜索法。著名的Baarda数据探测法就是均值漂移模型的一个典型的实际应用。1968年，巴尔达（Baarda）提出了一套粗差检测的理论和方法。时至今日，粗差探测仍是测量数据研究热点之一［2］。

基于方差膨胀模型的抗差估计也叫稳健估计，是指在测量数据存在粗差时，采用一定的估计准则，使参数估值尽可能接近最优的参数估值［3］。目前，在测量平差研究中，M 估计是使用最广泛、最简明的稳健估计法［4］，M 抗差估计的抗差性和效率与等价权函数及其临界值的合理性和参数初值的可靠性有关［5］。常用的等价权函数有L1 法、L1-L2 法、Tukey 法、Danish 法、Fair 法、Cauchy 法、Hampel 法、IGG 方案和IGG3方案等［6］，其中，IGG3 方案是杨元喜院士提出的相关抗差估计解式，近年来得到了广泛应用［7-11］。

1 Baarda数据探测法粗差探测

Baarda 数据探测法由荷兰的Baarda 提出［12］，Baarda 粗差探测的是以标准化残差为统计量，根据标准化残差大小，判断观测值是否包含粗差，将粗差剔除后重新平差。在最小二乘平差中，当一个观测值含有粗差时，会导致多个观测值的标准化残差超限。实际计算时，是将绝对值最大且超限的观测值剔除，然后再进行平差和数据探测，直到所有的残差均不超限，最后用没有粗差的观测值进行平差。

设误差方程式为：

式中：V是n维观测值残差向量；A是n×t阶系数矩阵；是t维参数估值向量；L是n维观测值向量。设观测值的权矩阵为P，P是对角阵。

由式（1），参数的最小二乘解为：

将代入式（1），可求得最小二乘残差V。又知V的权逆阵为

QV的对角线元素qv1，qv2，…，qvn是观测值残差v1，v2，…，vn的权倒数。当观测值独立时：

构造标准化残差统计量：

式中，σ0为先验单位权中误差，vi为第i观测值的残差，qvi为残差协因数阵QV主对角线上第i个元素的值。观测值没有粗差时，wi是服从标准正态分布的随机变量，当|wi|大于给定的限值（如2或3）时，即认定观测值Li存在粗差。

2 抗差M估计

设有误差方程式（1）为当观测值中含有粗差时，参数的最小二乘（LS）解必然受到歪曲。为求抗差解，一般将中的V2i用其他稳健函数代替，如|V2i|或ρ(Vi)，选择不同的函数，其抗差能力也不一样。

M估计极值函数：

式中，pi是Li的权。由误差方差（1）和极值函数（6）可得参数的抗差解为：

式中，为等价权矩阵。以表示的对角线元素，为：

式中，w是权因子函数，常用的权因子函数有Huber 函数、IGG1、IGG3 函数等。w()称为等价权因子；是标准化残差，即：

式中，vi是观测值残差，mvi是vi的中误差。mvi由下式计算：

式中：σ0是单位权中误差，可采用理论值或经验值；pi是观测值的权；Ai是矩阵A的第i行，即第i个误差方程的系数向量。

抗差估计实质是一个选权迭代的过程，具体步骤如下所示：

Step1：取k=0，参数的初值为X(k)=[x(1k)，x(2k)，…，x(tk)]T

Step2：计算残差V(k)=A X∧(k)-L

的权逆阵为：

单位权中误差公式为：

式中，n0是等价权因子等于零的观测值个数。

3 实验环节

3.1 实验说明

本次实验主要目的是对处理观测值中粗差常用的两种方法优劣性进行对比。对于粗差的探测，本次实验采用的是Baarda数据探测法进行粗差探测。对于本次实验，其中，实验参数σ0=1.4''，标准化残差|wi|的限差值设置为3，当标准化残差大于3 时，判定观测值存在粗差，将含有粗差的观测值剔除。

本次抗差估计采用的是M 抗差估计，关于抗差估计中的权函数选择的是由杨元喜院士提出的IGG3 方案，其中，观测数据按照质量高低划分为3 类：有效信息、可利用信息和有害信息。对于有效信息，采用最小二乘（LS）估计法，采用降权估计处理可利用的信息，采用零权估计处理有害信息。

其中，IGG3权函数如下所示：

式中，k0、k1为调和系数，将分成3段，依次对应有效信息、可利用信息和有害信息。在实际计算中，k0的取值范围为1.0～1.5，k1的取值范围为2.5～3.0，是标准化残差，，其中，σ0是单位权方差因子。对于本次实验，调和系数k0=1.5，k1=2.5，σ0=1.4''，且迭代收敛条件ε=0.002。

3.2 算例分析

为了比较Baarda 粗差探测和M 抗差估计效果，本文模拟测角网进行了实验和分析，测角网示意图如图1所示。图中，A、B、C、D这4点为已知点，P1、P2为未知点，为获得未知点的坐标，独立等精度观测了18 个角度，测角中误差为m=±1.4"，以坐标平差法平差该网，并对误差方程线性化处理［5］。

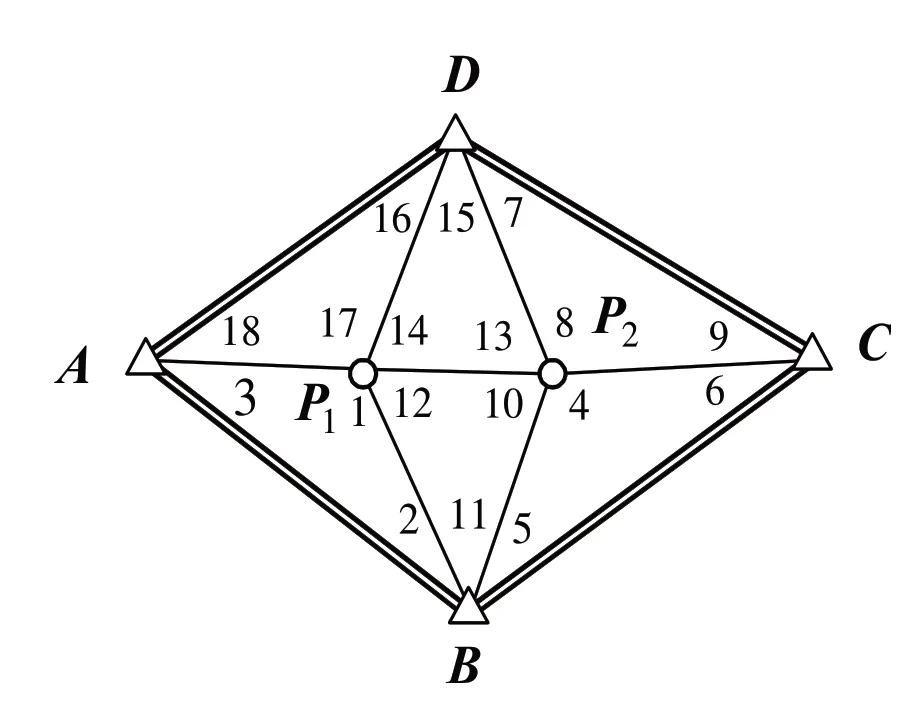
图1 测角网示意图

3.3 实验方案实施及结果分析

本实验主要目的是比较粗差探测和M抗差估计粗差探测的能力。因此，首先，最小二乘平差进行平差，得出最佳估值；然后，按照预设方案，向观测数据中加入粗差，再使用最小二乘平差，并同时采用Baarda数据探测法进行粗差探测和IGG3方案进行M抗差估计；最后，分别将各方案结果与正常模式下最佳估值进行比较。

本实验的粗差加入方案为：（1）在观测值L2中加入5''的粗差；（2）在观测值L2、L9中分别加入5''和10''的粗差；（3）在L2、L9、L15中分别加入5''、10''和15''的粗差；（4）在观测值L13、L14、L15中分别加入5''、10''和15''的粗差。

依据粗差加入方案进行的实验结果如表1所示。在本次实验中，进行方案（4）时发现在进行粗差探测时探测失败，粗差探测只探测出了L14、L15观测值含有粗差，没有探测出L13，出现了漏判的现象。为寻求原因，又增加两组实验进行粗差的探测：（5）在观测值L8、L14、L15加入粗差；（6）在观测值L5、L14、L15加入粗差。实验（5）和实验（6）的结果如表2所示。

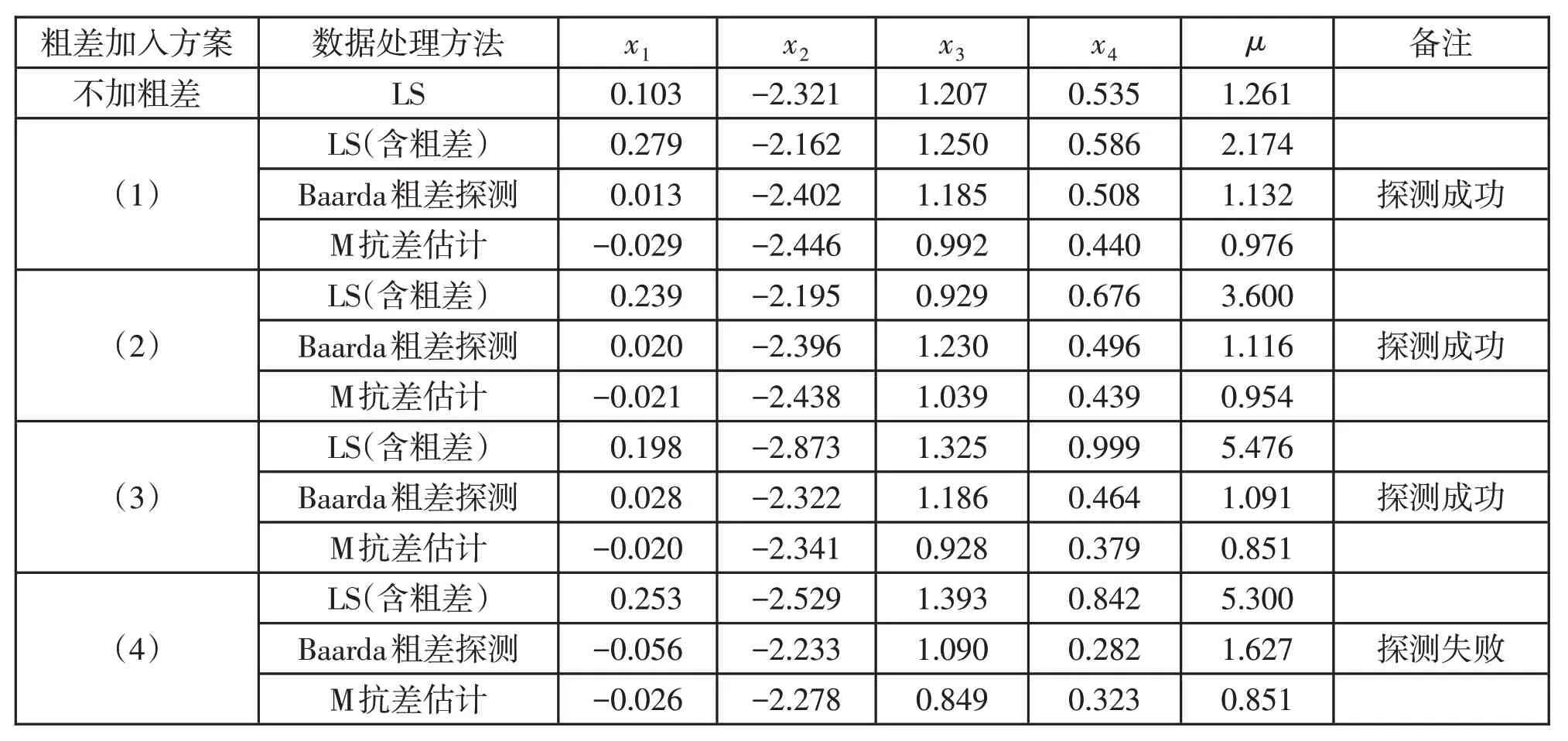
表1 不同方案粗差处理结果与正常模式下的参数估值的比较

表2 实验（5）、实验（6）结果

分析上述实验结果，可得出以下结论。

（1）随着加入粗差数目的增加，由最小二乘平差（LS）得到的参数的估值偏差也越来越大，结果表明，最小二乘平差（LS）已经不再适用于对未知参数进行估计。

（2）粗差探测和M 抗差估计都可以有效地减小粗差对观测数据的干扰，获得较为可靠参数估计值，但是，粗差数目的增加使得两种方法的效果都在下降。

（3）另外，从前3 组实验结果来看，M 抗差估计比Baarda 粗差探测效果好，得到的结果和正常模式下的参数估值更加接近，且在第4 组实验中进行粗差探测时出现了漏判的现象，导致探测失败。为寻求原因，又增加两组实验进行粗差的探测。由表2可知，新增的两组实验结果很好分析的原因，粗差探测的效果和含有粗差的观测值的分布有关，第4 组实验中加入粗差的3个观测值是同一个三角网的3个角度观测值，而新增的实验粗差加入的位置更加的均匀，所以，粗差探测的效果更好。

4 结语

本文选用Baarda数据探测法和M抗差估计并同时选择IGG3作为权函数进行粗差探测，并结合实例进行了实验对比。实验结果表明：粗差探测的效果和含有粗差的观测值的分布有关，M 抗差估计的效果与等价权函数及其临界值的合理性有关，总体来讲，M抗差估计粗差探测效果优于Baarda粗差探测。