微纳成型力学

2022-04-08 08:08吴伯朝

力学进展 2022年1期

吴伯朝鲁才刘泽 ,2,*

1 武汉大学土木建筑工程学院工程力学系, 武汉 430072

2 武汉大学水资源水电工程科学国家重点实验室, 武汉 430072

1 引言

随着产品小型化的发展趋势, 微加工技术变得日益重要 (Engel & Eckstein 2002, Fu & Chan 2013). 尽管基于光刻术的微加工技术已经在微机电系统 (MEMS) 、半导体及微电子芯片等领域取得重要而广泛的应用, 但因其受限于硅基材质, 且光刻技术本质上是一种平面微加工工艺, 因此, 应用光刻技术制造基于其他材料的三维几何零部件还存在极大挑战. 微纳成型是指利用材料的塑性变形直接制备出至少两个维度的尺寸都在微纳米尺度的零部件或结构的过程. 微纳成型由于其生产效率高、成本低等特点, 为微纳零部件的制备提供了一种极具前景的微加工方法(Fu and Chan 2013). 然而, 自20 世纪90 年代被提出以来, 微成型技术尽管引起了业界的广泛关注, 但在继续小型化时面临一个关键问题, 即尺寸效应 (Vollertsen et al. 2006). 首先, 各种作用力呈现明显的尺寸效应

其中m,g,γ,η,u,τs,τcs分别为质量、重力加速度、表面张力、黏度、平均流速、界面剪切强度和滑移面上的临界切应力. 随着特征尺寸 (L) 的减小, 比表面积显著增大, 重力作用(Fg) 可以忽略, 表面张力(Fγ) 、黏性力(Fη) 、界面摩擦力(Ff)及滑移面上的临界滑移力 (Fslip) 作用显著提升. 另一方面, 当零部件的特征尺寸小至微纳米尺度时, 相似原理不再适用, 即大尺度的成型模型不能直接用于小尺度. 例如, 当特征尺寸小至可与材料的晶粒尺寸相比拟时, 材料本身的力学性质会发生显著变化, 可以预见, 微纳米尺度下的成型机理也将发生相应改变. 此外, 当考虑界面接触状态时, 边界条件在模型缩放时也将发生变化.

目前, 已被成功应用的微纳尺度的成型技术主要是软光刻技术 (Zhao et al. 1997), 包括纳米压印光刻术 (nanoimprint lithography) (Chou & Krauss 1997; Chou et al. 1995, 1996)、微接触压印(microcontact printing) 、微转移铸造 (microtransfer molding) 等. 典型的纳米压印光刻术原理如图1(a) 所示, 把硬的纳米模板压入到Si 基底表面的聚合物PMMA 中, 由于PMMA 在加热到其玻璃转变温度 (Tg) 以上时会由硬弹性转变为黏性主导的类流体行为 (图1(b)) , 因此, 在Tg以上通过接触变形容易在PMMA 表面压印出纳米图形 (图1(a)) . 复制出图形后, 对系统降温, 此时PMMA 恢复硬弹性, 使得高温下通过接触变形复制的纳米图形在室温下脱模后得以保持. 软光刻技术的基本原理是利用类流体材料的低黏滞阻力, 使其在远小于模具材料强度的应力作用下流动以填充型腔, 以一维轴对称管流模型为例 (管半径为R) , 其在柱坐标系下的控制方程为

图 1 纳米压印光刻技术.(a)典型的纳米压印工艺流程示意图(Chou &Krauss 1997,Chou et al.1995,Guo 2004): 在一定的压力和温度作用下把表面具有纳米图案的硬模具压入到聚合物(如PMMA)表面,随后降温后使得硬膜具与聚合物脱离(脱模),从而在聚合物表面获得复制的纳米图案,最后,应用氧等离子蚀刻去除压痕中的残留聚合物;(b)聚合物储能模量的温度相关性.聚合物在其玻璃转变温度Tg 以下表现为弹性,在玻璃转变温度及熔点温度Tm 之间表现为黏弹性,而在Tm以上表现为黏性行为(Chantiwas et al.2011)

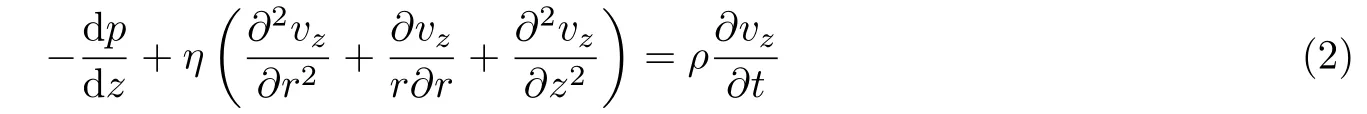
其中vz,p,ρ分别为流体沿管轴线方向的速度、压力和流体密度. 当雷诺数远小于1 时, 有=0,此处

自基于聚合物的纳米压印光刻术被提出以后, 人们进行了大量的数值模拟和实验研究, 探讨了纳米模具上图案的长细比、聚合物薄膜的厚度、施加的应力等对微纳成型的影响 (Heyderman et al. 2000, Hirai et al. 2001). 2009 年, Schroers 及其合作者 (Kumar et al. 2009, Schroers 2010, Schroers et al. 2011) 利用非晶合金 (金属玻璃) 在加热到其玻璃转变温度以上也能转变为高黏流体的特性, 率先应用阳极氧化铝纳米模板将非晶合金进行纳米模铸, 实现了高长径比非晶合金纳米柱阵列的制备. 此外, 人们也曾尝试在晶体金属的熔点温度以下对晶体金属进行纳米压印(Buzzi et al. 2008, Gao et al. 2014, Saotome et al. 1998), 但仅制备了特征尺寸在晶粒尺寸量级的微结构, 且由于硬模具是通过粒子束刻蚀制得, 导致所制备的微结构长径比较小. 关于晶体金属纳米压印过程的分子动力学模拟表明, 随着尺寸的减小, 所需的成型压力越大 (Hsu et al. 2005, Pei et al. 2007). 一般认为, 晶体金属的成型性能随着特征尺寸 (零部件的几何尺寸或晶粒尺寸) 的减小而显著降低 (Csikor et al. 2007, Kumar et al. 2009, Saotome et al. 1998, Uchic et al. 2004,Vollertsen et al. 2004), 因此, 在远低于熔点的温度下应用纳米压印技术直接在晶体金属表面获得小于其晶粒尺寸的纳米图形存在原理上的困难. 最近, 作者课题组的系列研究表明, 在低温条件下对晶体金属实施纳米压印, 确实是尺寸越小, 成型能力越差 (Liu 2019, Xu et al. 2020), 然而, 当提高成型温度到T＞ 0.4Tm时, 纳米模铸晶体金属将变得越小越容易, 该方法使得低成本、高效率且可控地制备超高长细比 (约2000) 以及直径可小至约5 nm 的金属纳米线阵列成为可能 (Liu 2017). 考虑到上述晶体金属纳米结构的制备源于块体晶体金属的剧烈塑性变形, 为区别于流体的纳米压印技术, 可称晶体金属在远低于其熔点温度下的纳米压印技术为超塑性纳米压印术(superplastic nanoimprinting, 或超塑性纳米模铸术, superplastic nanomolding) (Liu 2017).

近二十年来, 应用纳米压印技术制备各种纳米结构取得了较大的进展, 可进行纳米压印的材料体系不断丰富, 从最初的聚合物、非晶合金到纯金属、固溶体、高熵合金、有序相等. 这一低成本高效率的可控制备技术极大促进了微纳米结构材料在能源、高效催化、表面等离子体光学、纳米电子学及微纳机电系统等领域的广泛应用. 因此, 本文将针对微纳成型技术的最新研究进展, 聚焦不同材料在微纳成型过程中的变形机理及尺寸效应进行综述. 最后, 将针对金属微纳成型工艺面临的技术挑战及其关键力学问题进行展望.

2 聚合物的微纳米成型

聚合物材料的微纳米压印成型, 主要利用了其在高于玻璃转变温度时呈现出类流体特性, 且流动阻力随着温度的上升而显著降低. 一般地, 当非晶态材料加热至其玻璃转变温度以上时, 即T＞Tg, 其黏性系数 (η) 符合Vogel-Fulcher-Tammann (VFT) 公式 (Debenedetti & Stillinger 2001)

其中T为绝对温度;A,B是依赖于温度的常数,T0为参考温度. 由于黏性系数与系统的弛豫时间密切相关, 而弛豫时间与黏性系数一样, 也常用于刻画系统在原子/分子尺度上的动力学行为, 因此等价地, 非晶材料也通常由弛豫时间-温度关系即Williams-Landel-Ferry (WLF) 方程 (Williams et al. 1955) 进行描述

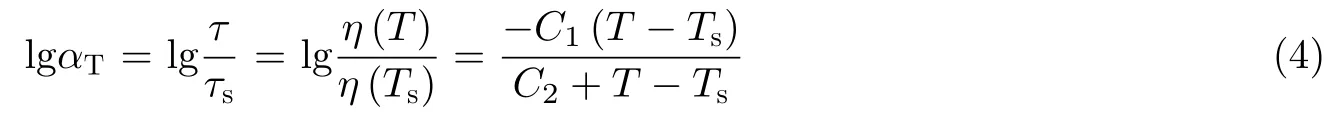
其中τ为非晶态材料的响应时间, 下标s 表示参考值. 若Ts=Tg, 则C1= 17.44,C2= 51.6 K(Scheer & Schulz 2001).

在聚合物的微纳成型中, 聚合物的流变行为将直接影响所制备的零部件的品质. Heyderman等 (2000)、Scheer 和 Schulz (2001) 采用具有微米尺度图案的模具, 在玻璃转变温度以上对聚合物压印成型进行了系统的实验研究, 通过分析PMMA 薄膜 (厚度约为200 nm) 在相同孔腔高度(175 nm) 但不同宽度 (6、10 和20 μm) 的型腔中的填充过程, 观察到一种“双峰”变形模式(图2(a)), 即PMMA 在热压作用下从孔腔边缘进入并沿与孔壁垂直的方向变形 (Heyderman et al. 2000). Scheer 和Schulz (2001)通过对不同厚度的聚合物薄膜 (500 nm 和4 μm) 进行压印，发现上述“双峰”变形模式只有在压印薄膜时才出现, 这是因为腔外薄膜流动会挤压腔内薄膜从而导致孔腔入口侧壁附近的聚合物薄膜发生局部受压屈曲.Cross 等(2003) 在等温压印实验中也观察到了类似的“双峰”变形模式. 上述研究表明聚合物的变形模式与薄膜厚度及模具的孔腔尺寸密切相关. 随后, Rowland 和 King (2004)在PDMS 的玻璃化转变温度附近 (Tg- 10 °C ＜T＜Tg+ 20 °C) 进行系统的压印实验, 如图2(b) 所示, 他们通过改变压印时间、温度和模板孔腔的宽度, 观察到了聚合物在压印过程中不同阶段的变形. 同时, 他们也发现, 对于高为4 μm 的孔腔, 当宽度为50 和100 μm 时, 会出现“双峰”变形模式, 而当孔腔宽度为30 μm 时, 则为“单峰”变形模式(图2(c)) . 总之, 在微米尺度下聚合物的热压印过程中, 黏性流动、局部应力状态和剪切稀化起主导作用, 其流动特性适用于高温短时间热塑性压印. 此外, 黏性系数作为衡量热塑性材料流动性能的一个重要参数, 可通过填充效率进行估算 (Rowland & King 2004)

图 2 聚合物在微米尺度热压成型过程中的变形模式.(a)PMMA 和(b)PDMS 表面通过热压印复制的微米结构的SEM 图(Heyderman et al.2000,Rowland &King 2004),(c)热压印过程中,聚合物填充模板孔腔的两种典型变形模式(Rowland &King 2004)

其中p是压印时的压强,Afill为填充面积百分比,t为压印时间.

除了通过实验研究聚合物微纳米成型过程中的流变机制, 人们还应用数值仿真手段模拟了聚合物薄膜的微纳米成型过程 (Hirai et al. 2001, 2004; Juang et al. 2002). 例如, Hirai 等(2001,2004)通过有限元仿真模拟了各种压印条件 (模具孔腔的深宽比, 聚合物薄膜的初始厚度和成型压力) 下聚合物薄膜在玻璃转变温度以上的流变行为 (图3(a) ~ (c)) , 通过输出压印过程中不同阶段的聚合物截面轮廓并与实验进行比较, 定量评估了聚合物进入模具孔腔的截面渗透率和聚合物的残余厚度, 结果表明压印所需的压力和模具孔腔的填充率显著依赖于图案的长宽比、聚合物的初始厚度和图案的占空比: 对于深宽比很大或很小的图案, 所需的压印压力都会增大, 这与实验观察吻合; 当聚合物的初始厚度减小至模具孔腔高度的两倍以内时, 所需的压印压力也会增大 (Heyderman et al. 2000, Rowland et al. 2008). Jeong 等(2002)在模拟中考虑了毛细力和模具孔腔宽度对聚合物流动行为的影响, 结果表明, 在大孔腔宽度、压印速度慢且表面张力不显著(即黏性力显著大于表面张力) 的条件下才会出现“双峰”变形模式, 此时的填充以压力驱动下的横向流动模式 (拉伸流和剪切流) 为主, 在孔腔中则为塞流模式 (图3(d)) . 为了衡量纳米压印过程中毛细力的影响, Rowland 等(2005)计算了不同特征尺寸下压印过程的毛细管数Ca=ηVNIL/σ, 式中VNIL为纳米压印过程中的特征速度,σ为表面张力, 并与实验进行对比, 发现毛细管数除了可用于预测聚合物的流动机制, 对聚合物的变形模式也起着关键作用. 由于毛细力显著依赖于表面润湿性能, 且尺寸越小, 其作用越显著 (式 (1) ) , 人们通过调控表面润湿性能, 开发了毛细力光刻技术 (capillary force lithography) 用于制备具有高分辨率的聚合物模板 (Bruinink et al. 2006, Suh et al. 2001, Suh & Lee 2002). 需要指出的是, 毛细现象的存在也为图案的可靠制备带来了挑战, 例如, 高长径比的图案容易发生团簇 (Stoykovich et al. 2003); 退火会造成压印图案边和角的平滑化 (Chao & Guo 2004, Chou & Xia 2008), 甚至使得图案的几何特征消失 (Ding et al.2007, Jones et al. 2006).

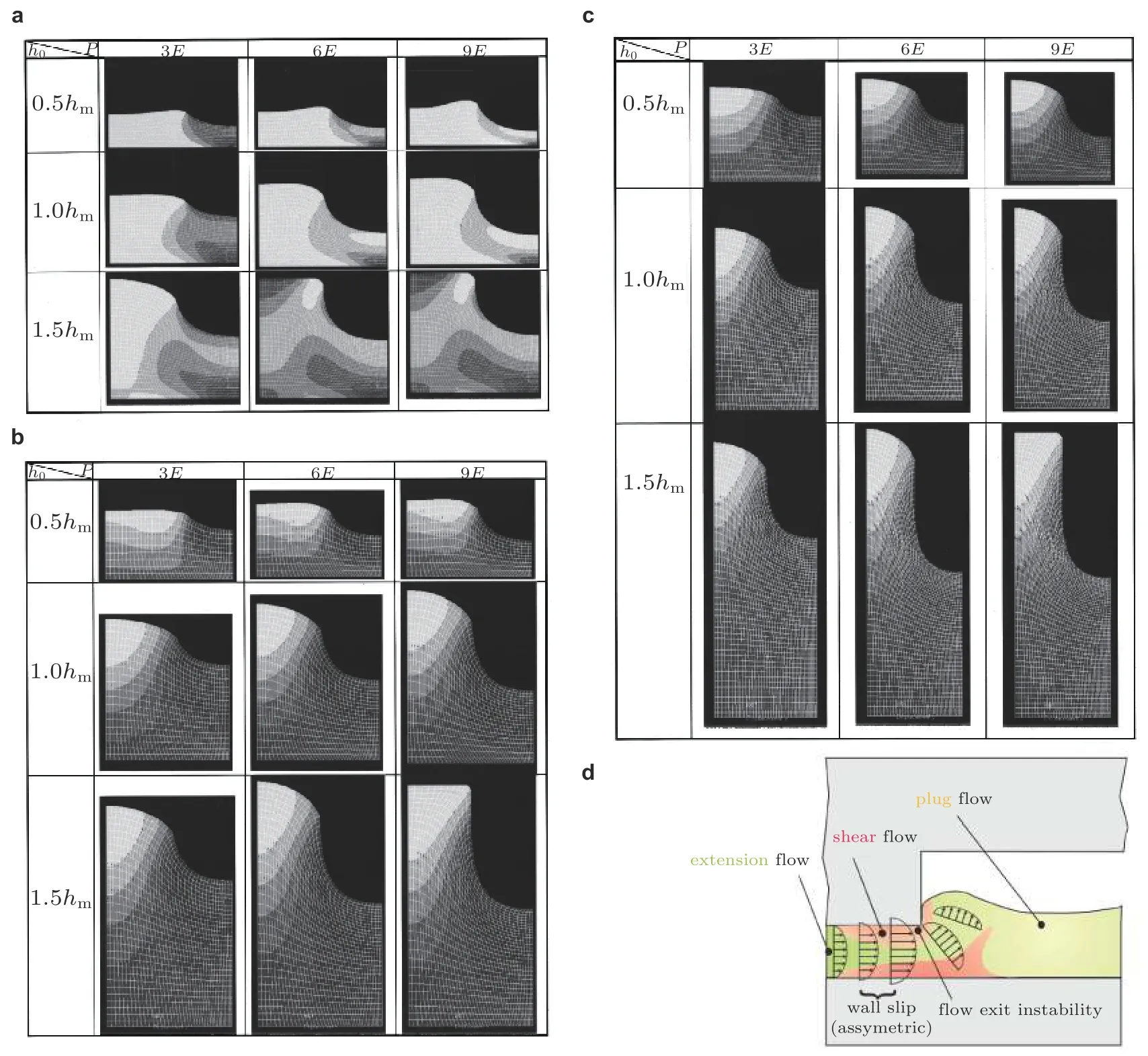
图 3 (a)~(c)有限元模拟聚合物在微成型过程中流入单一孔腔过程中的截面轮廓和主应力分布,孔腔的深宽比分别为:(a)0.5,(b)1.0 和(c)1.5.图中h0 表示聚合物薄膜初始的厚度,hm 表示模具孔腔的深度.P 为压印时的压力,E 表示聚合物的弹性模量(Hirai et al.2001);(d)宽孔腔入口附近聚合物流动示意图.压力梯度驱动下的聚合物流动将在入口处同时产生剪切和拉伸流,在出口处则出现塞流现象(Cross 2006,Schulz et al.2006)

考虑聚合物的黏弹性行为, Takagi 等(2008)分别采用线性和广义麦克斯韦模型研究了纳米压印过程中聚合物 (cyclo-olefin-polymer, COP) 变形的时间依赖性 (图4(a)). 聚合物剪切模量随时间的关系可表示为

图 4 (a)描述聚合物黏弹性行为的标准线性模型(左)和广义麦克斯韦模型(右);(b)聚合物变形随时间变化的数值模拟结果.成型压力为1.25 MPa,保持时间分别为10 s,30 s 和60 s;(c)~(f)热压印COP 后的表面SEM 图像.热压印压力为1.25 MPa,保持时间分别为10 s(c),30 s(d),60 s(e)和120 s(f)(Takagi et al.2008)

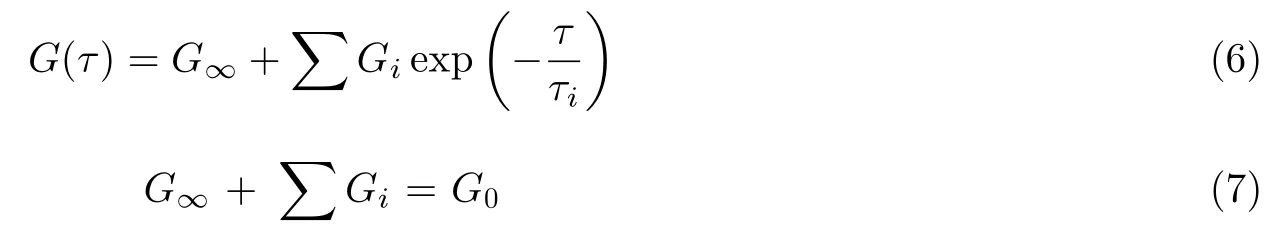
采用瞬时剪切模量G0对式 (6) 进行无量纲化有

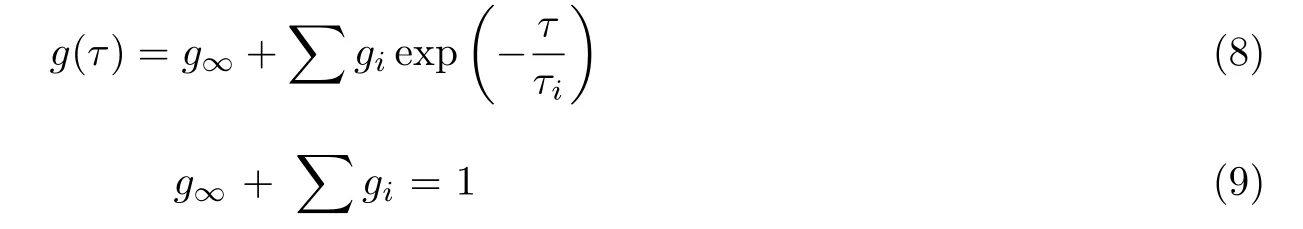
在数值模拟中, 弛豫时间-温度的关系通过式 (4) 获得, 从而聚合物的剪切模量与温度的关系可表示为

图4(b) 为聚合物在压印时的变形随时间变化的数值模拟结果. 压印过程中聚合物的变形随着保载时间的延长而增大, 这与实验结果一致 (图4(c) ~ (e)) (Takagi et al. 2008), 同时, 结果表明在描述聚合物随时间的变形时, 采用广义麦克斯韦模型更加合理.

3 非晶合金微纳米成型

非晶合金作为另一种非晶态材料, 又称金属玻璃 (metallic glass, MG) (Schroers & Paton 2006), 由于其内部原子是无序排列的, 因此金属玻璃相比晶态金属具有高强度、高弹性极限和抗腐蚀耐磨损等优异的力学性能. 基于上述优点, 金属玻璃被广泛用于电子设备 (如移动手机)的外壳 (Schroers 2005)、医疗器材、珠宝以及体育器材等商业应用 (Telford 2004). 金属玻璃另一个独特的优点是可热塑性净成型特性 (superplastic formation, SPF) . 由于金属一般具有较高的熔点, 因此加热金属到其熔点以上进行浇铸成型既不节能也对模具材料耐温性提出了苛刻要求, 且该工艺应用于金属玻璃时受到需要快速冷却以避免结晶的技术挑战 (图5(a) 中的路径1)(Schroers & Paton 2006). 金属玻璃的热塑性成型是指加热金属玻璃至其超冷液相温度区间(SCLR: 即温度大于Tg而小于晶化温度Tx的区间) 进行成型制备零部件的过程 (图5(a)种的路径2) (Kawamura et al. 1995; Kumar & Schroers 2008; Kumar et al. 2010; Martinez et al.2008; Packard et al. 2009; Schroers et al. 2011, 2007c, 2004, 2002). 相比传统的材料如聚对苯二甲酸乙二醇酯 (PET, 一种热塑性树脂) 、可超塑性成型合金 (SPF, 典型的如2004 铝合金) 和不锈钢, 金属玻璃 (如图5(b) 中的Zr-BMG 和Pt-BMG) 在其Tg以下具有优于不锈钢的高强度, 而在其超冷液相区具有与热塑性树脂可媲美的成型性能 (图5(b)) . 图中理想的成型区域一般是根据材料的流动性划分 (典型的如固体的强度、流体的黏性系数) , 要求在实际成型时间尺度上可以忽略湍流、表面张力和重力等因素的影响 (Schroers et al. 2011).

金属玻璃热塑性成型最早可追溯到1978 年, Patterson 和 Jones (1978)设计了一种简单的加工装置, 采用压力弹簧提供压力, 将装置与Fe40Ni40P14B6金属玻璃一同放置在马弗炉中, 保持恒温条件, 拔出冲头的插销, 在压力弹簧的带动下, 冲头冲压样品，冷却后得到无定型的柱状结构.随后, 大量学者进行了相关研究, Kumar 等 (2009) 通过热塑性成型制备了金属玻璃微齿轮(图6(a)) ; Schroers 等(2007b)制备了微扭簧 (图6(b)) ; Nishiyama 和 Inoue (1999) 使用热机械测试方法, 研究了Pd40Cu40Ni10金属玻璃黏度与加热速率、外加应力的关系, 并采用热塑性成型技术加工出了三级齿轮; Sojiema 等 (2005)测量了锆基金属玻璃在其过冷液相区的应变率敏感系数m,用以评价其成型能力. 此外, Schroers 等(2007a)采用Pt57.5Cu14.7Ni5.3P22.5和Au49Ag5.5Pd2.3Cu26.9Si16.3等金属玻璃颗粒为原料, 在较低的压力下通过热塑成型制得致密紧实且表面光洁的零部件, 其力学性能同块体材料相当 (图6(c)) , 随后又用热吹塑的方法对Zr44Ti11Cu10Ni10Be25金属玻璃进行了热塑性成型, 塑性变形超过500% (图6(d)) , 并发现基于牛顿流体的吹塑模拟结果与实验吻合很好 (Schroers et al. 2007c). 除此之外, 考虑到高温可能导致的金属玻璃的氧化行为, 人们也开发出低温下基于超声振动诱导金属玻璃塑性变形的成型方式, 该方法被称为超声辅助成型 (ultrasonic beating formation, UBF) (Li et al. 2020, Ma et al. 2015).

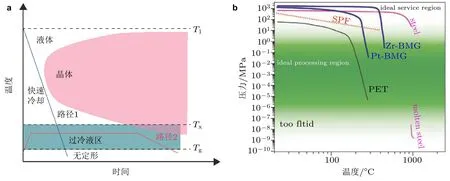
图 5 (a)金属玻璃的时间−温度−转变示意图.路径1 和2 分别给出了金属玻璃浇铸和热塑性成型两种方式.路径1 的成型方式要求快速冷却以避免结晶,因此成型时间短; 路径2 给出的成型过程不需快速冷却,因此成型时间窗口长(Schroers 2005,Schroers &Paton 2006);(b)金属玻璃与不锈钢、可超塑性成型合金以及热塑性树脂的强度与可成型性能比较(Schroers et al.2011)

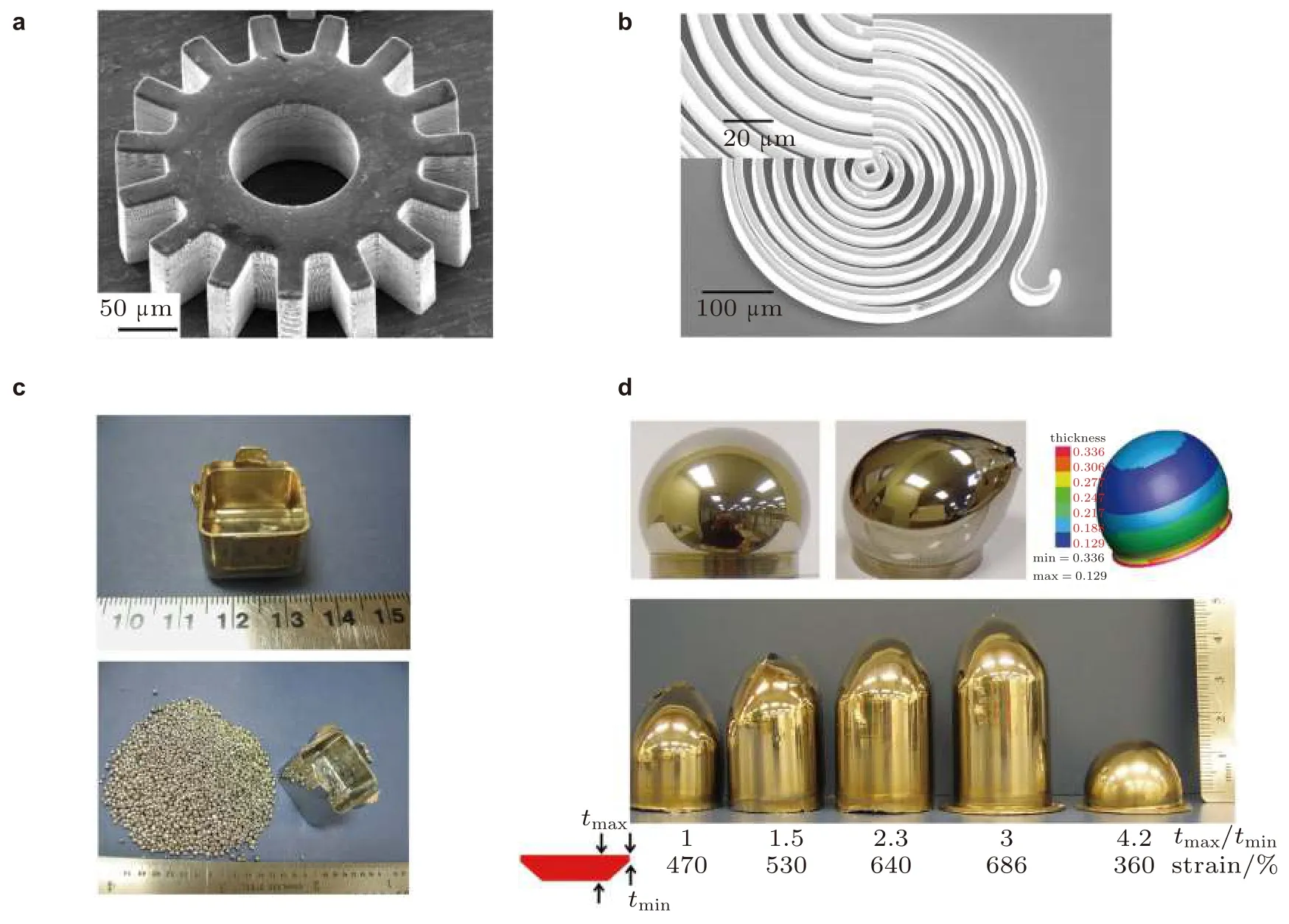
图 6 (a)Pt57.5Cu14.7Ni5.3P22.5 金属玻璃微齿轮(Kumar et al.2009);(b)线圈形状微弹簧(Schroers et al.2007b);(c)上图为对Au49Ag5.5Pd2.3Cu26.9Si16.3 金属玻璃粉末进行的热塑性模铸成型,成型温度和压力分别为150 ℃和100 MPa,持续时间200 s,下图为对Pt57.5Cu14.7Ni5.3P22.5 金属玻璃粉末在270 ℃和28 MPa 压力下进行的热塑性模铸成型,持续时间100 s(Schroers et al.2007a);(d)在压力差105 Pa 和温度460 ℃下通过吹塑法制备的Zr44Ti11Cu10Ni10Be25 金属玻璃球壳结构,塑性变形可超过500%(Schroers et al.2007c)

一般来说, 金属玻璃的超冷液相区越宽, 在该范围内的黏性系数越低, 其热塑性成型能力越好. 数学上, 可以用成型试样中某一点的最大应变值来衡量金属玻璃的成型能力. 在小应变率下,金属玻璃在其超冷液相区可用牛顿流体描述, 如Zr35Ti30Be26.75Cu8.25金属玻璃在温度为370 ℃且应变率为10-3s-1时表现为牛顿流体行为 (Li et al. 2013), 此时, 其本构方程为

其中σij,p,δij,η,Dij分别为应力张量、静水压力、克罗内克符号、黏性系数和变形率张量. 故成型试样中某一点在成型过程中的累计变形量为

对于单轴拉伸试样, 在给定成型温度和压力条件下, 根据式 (12), 易得金属玻璃在发生晶化前可达到的最大应变 (εmax) 为 (Schroers 2008, Schroers et al. 2007c)

式中:tcryst表示金属玻璃在过冷液相区发生结晶时的时间 (Schroers 2008, Schroers et al. 2007c),上式忽略了部分晶化对黏性系数的影响. 式 (13) 中, 只有tcryst和η为材料的本征属性, 它们的比值越大, 表示在相同成型条件下, 该金属玻璃的变形量越大, 即成型性能越好. 对于恒升温速率下的成型过程 (即T˙为常数) , 可一般地定义金属玻璃的成型性能为

式(14)应用于金属玻璃薄半球壳的恒升温速率吹塑实验, 可得 (Ding et al. 2014)

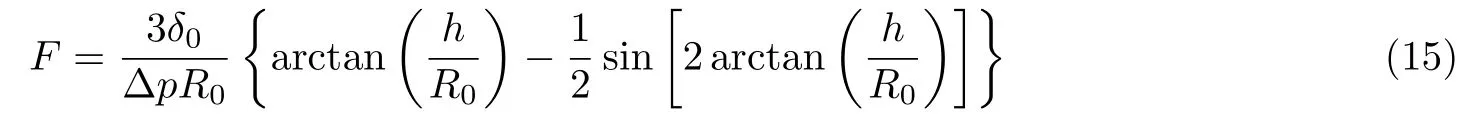
式中 Δp,δ0,h,R0分别为球壳内外压力差、初始膜厚、球壳高和半径. 该式可以方便地把特定条件下金属玻璃的成型能力与实验可测的吹塑几何尺寸建立关系, 从而可用于最优成型能力金属玻璃成分的快速筛选 (图7) (Ding et al. 2014).

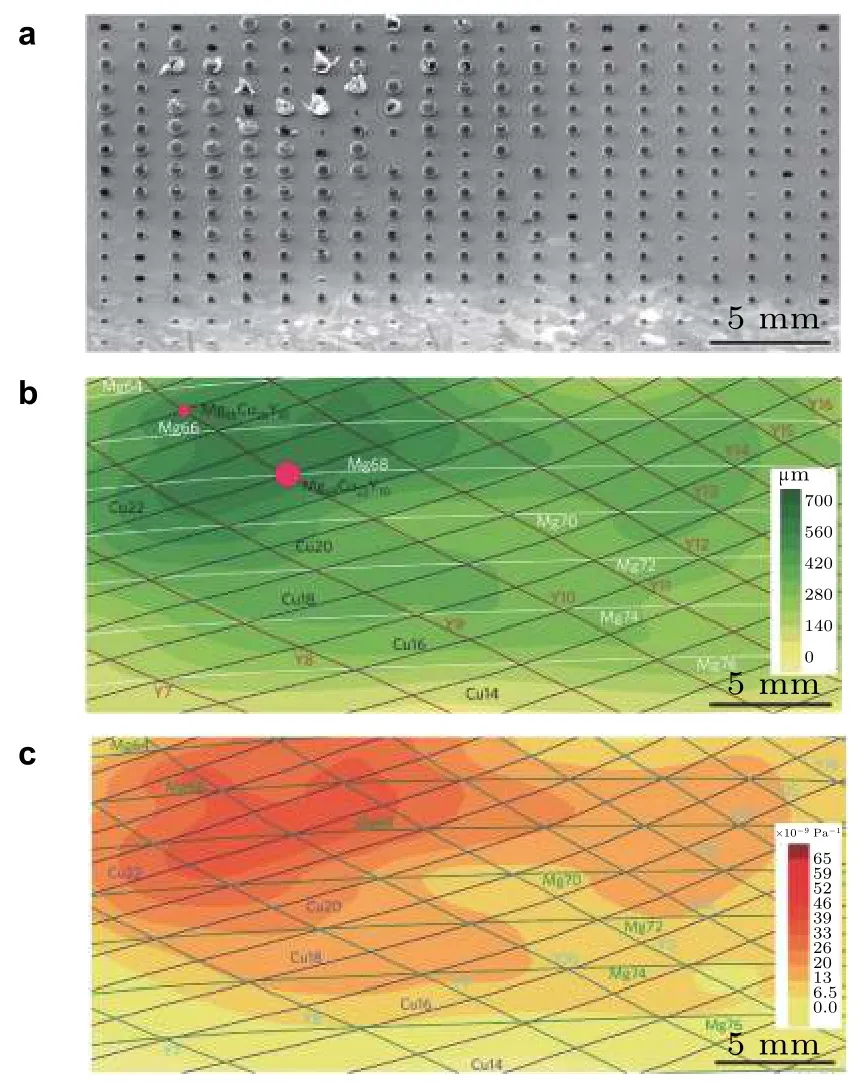
图 7 应用热吹塑成型实验筛选具有最优成型能力的金属玻璃组分(Ding et al.2014).(a)不同位置处的金属玻璃具有不同的成分,它们在相同条件下热吹塑后得到不同大小的球壳;(b)对(a)中区域进行成分分析,然后对比(a)图中热吹塑后最大的球壳所在的位置,获得最优成型性能的金属玻璃成分为Mg68Cu22Y10;(c)应用方程(15)可量化不同成分的金属玻璃的热塑性成型能力,可知不同位置处各原子的百分比含量仅发生较小的变化,但热塑性成型能力存在超过一个数量级的差异

相比聚合物非晶材料, 金属玻璃的流动单元可小至原子尺度, 因此应用金属玻璃的热塑性成型特性, 原则上可以制备特征尺寸任意小的纳米结构, 并且尺寸越小, 金属玻璃越软, 即成型能力越好 (Huang et al. 2007). 然而, 直到2009 年, Schroers 课题组 (Kumar et al. 2009; Schroers 2010;Schroers et al. 2011, 2007a, 2007b) 才首先应用纳米压印技术制备了长径比可超过10 而直径可小至13 nm 的Pt57.5Cu14.7Ni5.3P22.5金属玻璃纳米柱阵列 (图8(a)) . 随后, Liu 等实现了非贵金属基金属玻璃 (如锆基和镁基金属玻璃) 纳米柱的制备 (图8(b)) (Liu & Schroers 2015).

在金属玻璃的超冷液相区进行微纳成型, 可通过下述雷诺数对其填充流动行为进行预测

图 8 应用纳米压印术制备的(a)Pt57.5Cu14.7Ni5.3P22.5 金属玻璃纳米柱阵列(Schroers 2010,Schroers et al.2007b)和 (b)Zr44Ti11Cu10Ni10Be25,Mg65Cu25Y10金属玻璃纳米柱阵列 (Liu &Schroers 2015)

其中ρ,u,d分别为金属玻璃的密度、流速和模具的特征尺寸. 对于典型的金属玻璃微纳成型实验,ρ ＜20000 kg/m3,u＜ 1 μm/s,d＜ 10 μm,η＞ 1.0×105Pa·s, 则Re＜ 2.0×10-11, 因此金属玻璃在微纳成型过程中可视为层流. 当模具孔洞为圆柱形时, Schroers (2005, 2010) 通过改变孔径观察到热塑性成型后的金属玻璃微柱的长度与直径呈线性关系 (图9) , 该现象与Hagen-Poiseuille 管流模型预测结果一致

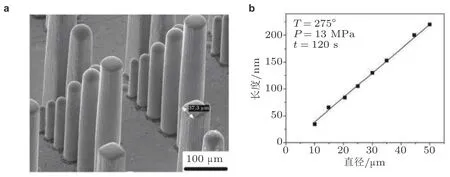
图 9 (a)应用变孔径硅模板热压成型制备的直径为10 ~ 50 μm 的Pt57.5Cu14.7Ni5.3P22.5 金属玻璃微米柱;(b)根据(a)图测得微柱的长度和直径的关系(Schroers 2005,2010)

式中p为施加的成型压力,t为热压时间.

然而, 当模具尺寸减小到5 μm 以下时, 微柱的长度与直径开始偏离线性关系 (Kumar et al.2011, 2009). 这是因为随着特征尺寸减小, 表面张力效应不能被忽略 (式 (1) ) , 此时, 需要在式(17) 中引入表面张力效应. 根据量纲分析, 容易获得考虑表面张力影响的Hagen-Poiseuille 公式

其中γ是金属玻璃的表面能,θ是金属玻璃与模具之间的接触角. Shao 等 (2013) 应用阳极氧化铝纳米模板对Pt57.5Cu14.7Ni5.3P22.5金属玻璃进行热压成型, 发现尺寸越小, 相同条件下, 纳米柱的长径比越小 (图10(a)) ,他们把该现象归因于纳米尺寸孔道对金属玻璃流动单元的限制导致流动阻力 (或黏性系数) 显著增大 (图10(b)) .

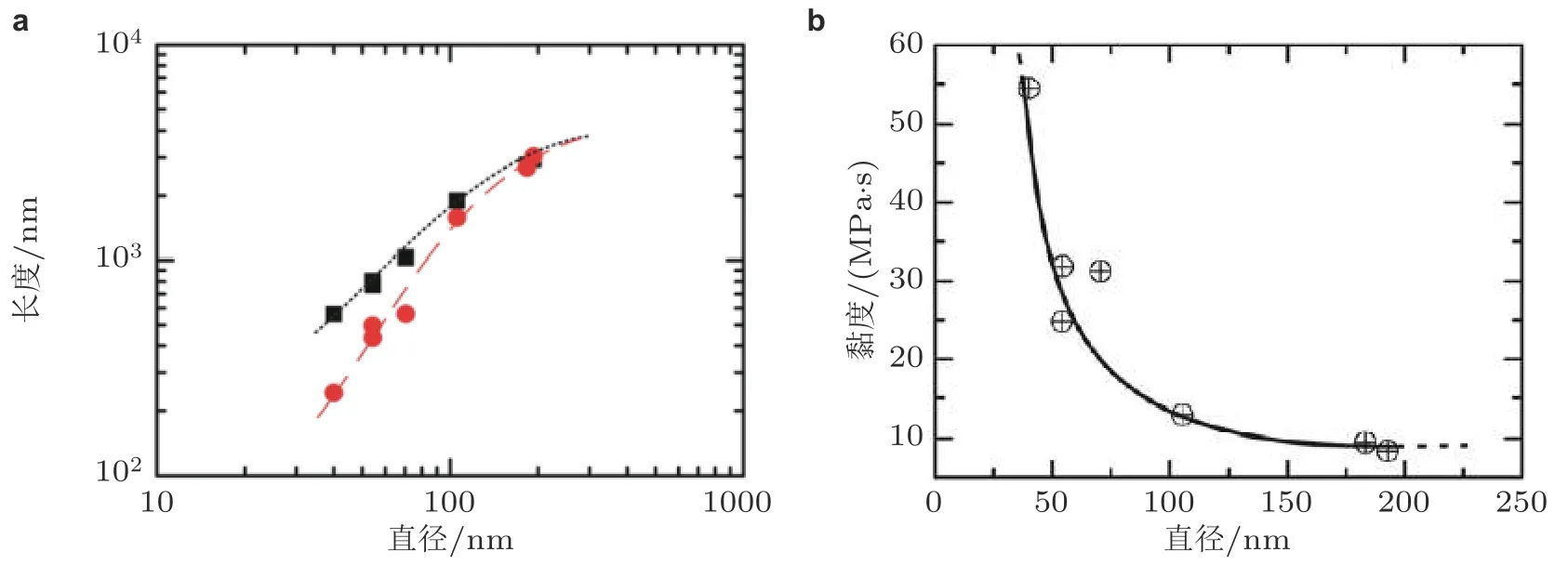
图 10 (a)热压纳米成型Pt57.5Cu14.7Ni5.3P22.5 金属玻璃制得的纳米柱长度与直径的关系,其中红点为实验数据,黑色点为根据式(18)计算得到;(b)实验数据与理论预测值的偏离源于纳米空间限制下黏性系数的显著增加(Shao et al.2013)

4 晶体金属的微纳米成型

以上关于聚合物或非晶合金的微纳成型都是应用了其在过冷液相温度区间表现为类流体的行为, 且其黏性系数随着温度升高呈指数下降 (式 (3) ) , 从而减少了材料流入模具孔腔的阻力,变得易于成型. 对于晶态材料, 材料软化通常需要加热到很高的温度, 例如, 不锈钢需要加热到800 ℃以上屈服应力才会发生显著下降 (图5(b)) , 尤其是考虑到晶态材料屈服应力的尺寸效应(即Hall-Petch 效应) (Greer & De Hosson, 2011)及其基于位错运动的变形模式 (Han & Yi 2021,Hou et al. 2009), 人们长时间以来认为在远低于晶体的熔点温度以下对晶体金属进行纳米成型是不现实的 (Csikor et al. 2007, Greer & De Hosson 2011, Uchic et al. 2004). Buzzi 等(2008) 曾尝试用硅模板压印金和银制备了长径比可达5 的微结构, 但因压印温度较低 (金与硅的共晶反应温度约为300℃) , 所制备的微结构的最小特征尺寸通常和晶粒尺寸是一个量级. 此外, 也有尝试通过激光冲击纳米压印制备金属微纳米结构的报道 (图11) (Cui et al. 2009, Gao et al. 2014), 该方法利用激光冲击形成的极高应变率 (105~ 107s-1) 来克服晶体金属在纳米尺度下的变形能力限制, 实现了长径比可达5 的金属纳米结构的制备 (图11(e)) . 最近, Liu (2017, 2019)的研究发现对于多数晶态金属材料, 当成型温度提高到0.5Tm附近时, 可以通过纳米模铸技术方便地制备出有序的且长径比L/d可高达约 2000 的金属纳米线阵列 (图12) (Liu 2017), 而纳米线的直径可小至5 nm(Liu 2019).

图 11 激光冲击压印制备金属纳米结构(Gao et al.2014).(a)(b)Ag 纳米结构;(c)(d)Al 纳米结构;(e)在Ag 表面形成的“V”形沟槽,其长径比可达5;(f)钛纳米沟槽结构

应用微纳成型工艺制备晶体金属纳米结构, 本质上是利用材料的塑性变形 (吴艳青等 2005).因此材料的塑性变形能力越好, 越容易制得金属纳米结构. 考虑到实验中很难测得成型试样中某一点的累计塑性变形量, 定义如下晶体金属的成型能力

式中,和分别为有效应力和有效应变,εapp为表观残余应变,为成型试样达到表观残余应变εapp所累积的有效应变. 由于成型过程中弹性变形通常可以忽略 (可近似认为材料的体积V0是一个常数) , 因此对于准静态的成型过程, 积分项反映了材料中一点达到表观残余应变所需要消耗的能量密度, 在εapp给定的条件下, 积分项越小, 材料的成型能力越好. 以短粗柱的压缩成型为例,实验上可以方便测得成型后短粗柱高度的相对变化量Δh/h, 而通过记录成型过程中的静态力-位移曲线 (包括加卸载过程) , 容易计算获得成型过程所耗散的外力功W=P ·dh-P ·dh,P为外载荷 (图13) . 此时, 式 (19) 可近似表示为

图 12 晶态金属的纳米模铸成型.(a)应用超塑性纳米模铸技术制备的金纳米柱阵列(比例尺为5 μm,插图的比例尺为30 nm);(b)直径为约200 nm 的铋金属纳米柱阵列(比例尺为5 μm,插图的比例尺为200 nm);(c)银纳米柱阵列,长径比高达约2000(比例尺为2 μm,插图的比例尺为25 nm);(d)(e)铜和铂纳米柱阵列(比例尺分别为200 nm 和100 nm)

晶体金属的成型性能越好, 在相同条件下进行纳米模铸越容易制得高长径比的纳米结构, 因此纳米结构的长径比一定程度上也反映了晶体金属的成型能力. 需要指出的是, 晶体金属的塑性变形机制相比非晶材料更加复杂. 一方面, 晶体金属的塑性变形机制包括位错形核及运动 (Schall et al. 2006, Yamakov et al. 2001, Zhu et al. 2008)、晶界滑动及迁移 (Langdon 1970, Voronov et al.2006, Wei et al. 2008)、孪生变形 (Wu et al. 2008, Zhu & Gao 2012, Zhu et al. 2013)、扩散蠕变和黏性流动 (Coble 1963, Herring 1950, Kim & Lu 2006, Mukherjee et al. 1969, Raj & Langdon 1989)等, 因此晶体金属的变形机制显著依赖于成型温度、成型应力及晶体的微结构 (如晶粒尺寸) .另一方面, 当应用微成型工艺制备金属纳米结构时, 由于模具的特征尺寸通常远小于材料的微结构尺寸 (Liu 2017), 因此, 必须考虑外部几何尺寸对成型工艺带来的影响.

一般而言, 在高应力和低温条件下, 晶体金属的微纳成型源于位错主导的变形机制, 而在低应力和高温下则是扩散主导的变形机制. 在扩散蠕变主导的成型高温区间 (通常T＞ 0.4Tm) , 晶体金属的塑性变形应变率为 (Frost 1982)

其中A1是取值约为1 的无量纲常数.Dl,σs,μ,b和kB分别是晶格扩散系数、等效应力、剪切模量、柏氏矢量幅值和波尔兹曼常数. 例如, 500 ℃下纯金中的自扩散系数约为10-17m2/s, 剪切模量约为27 GPa (Liu 2017), 柏氏矢量幅值为2.88 Å (1 Å = 0.1 nm) (Ashby 1972), 当σs= 200 MPa时, 由式 (21) 可以估算出应变率约为3.0×10-3s-1. 以一维纳米模铸模型为例 (图14) , 定义如下表观应变率

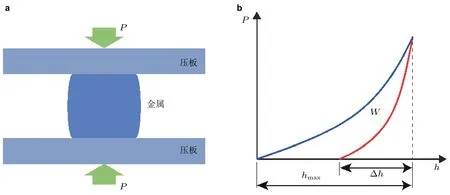
图 13 晶态金属成型能力实验设计.(a)平行板压缩实验构型;(b)典型的准静态加卸载曲线示意图,图中蓝线为加载过程,红线为卸载过程

则有L/L0=exp(ε˙t),代入典型的实验时间尺度t= 100 s 及ε˙=3.0×10-3s-1, 可得L/L0=1.35, 即经过100 s 的成型加载后, 纳米柱的长度会增长35%. 上述估计表明一旦成型压力能克服晶体金属进入纳米孔道中的初始势垒, 就能实现纳米柱的生长, 这就解释了图12 中多数金属在较高温度下 (一般在0.5Tm附近) 可以实现纳米铸造的原因 (Liu 2017), 尤其是当延长超塑性纳米模铸的时间后, 制备的银纳米线的长径比可高达约2000, 这远高于金属玻璃纳米成型所能获得的长径比, 其根源在于晶体金属本身具有很好的热力学稳定性, 因此成型时间不受限制, 而金属玻璃在热塑性成型过程中受到晶化时间的限制, 很难制备出具有较高长径比的一维纳米结构 (刘泽 2018).

考虑到纳米模铸过程中, 模具孔道尺寸远小于晶体金属的晶粒尺寸, 因此晶体金属进入纳米孔道的初始势垒可以通过估计单晶晶体在孔道入口附近的位错环形核应力得到 (Xu et al. 2020)

其中常数α 依赖于形核位错的类型及泊松比. 式 (23) 预测的关于孔道尺寸的标度律与Hall-Petch 效应类似, 为了克服入口处位错环的形核势垒, 模具孔道尺寸越小, 临界成型压力越大, 这与实验结果吻合 (图15(a)) (Liu 2019). 随着成型温度的升高, 上述临界成型压力降低了近一个数量级, 且对尺寸的依赖性显著降低 (图15(b)) , 这主要源于位错形核的热激活机制.

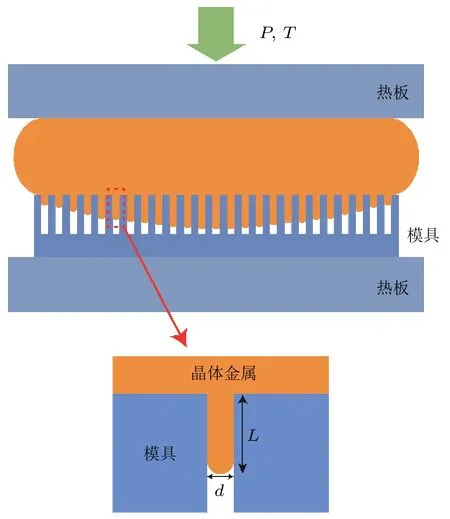
图 14 晶体金属的超塑性纳米成型模型

应用式 (21) 和式 (22) 于晶体金属的微纳米成型时没有考虑纳米孔道空间限制对材料变形的影响. 最近从实验上通过测量金属纳米柱的长径比, 探测了成型过程中金属材料的变形行为.典型的对于块体Au, 发现在相同的成型条件 (即温度约0.67Tm、试样几何、加卸载路径都相同)下, 纳米孔道的尺寸越小, Au 纳米柱的长径比越大 (图16 中红色数据点) , 这表明尺寸越小, Au的成型性能越好 (Liu et al. 2019), 该现象与金属玻璃的纳米成型规律完全相反 (Shao et al. 2013)(图16 中黑色数据点) .

为了理解上述实验现象, 首先通过分子动力学模拟对块体Au 的纳米模铸过程进行研究, 模型图如图17(a) 所示, 在700 K 成型温度下加载1 ns 的模拟结果如图17(b) 所示, 此时压入纳米柱子的长度约为35 nm (对应图中黑色点划线) , 然后在该位移载荷下保持0.5 ns, 统计位移载荷保持前后Au 原子沿着纳米柱轴线方向的分布, 可以看出在加载时轴向原子数分布 (或空位浓度)从纳米柱子的根部到尖端近似为线性分布 (尖端的非线性源于形状影响) , 而在位移保持过程中纳米柱子中的浓度梯度有所降低, 这主要是由应力松弛导致, 但柱子中的原子数分布仍然近似为线性 (对应图中红色点划线) . 考虑到高温下晶体中的空位不可避免, 而模铸过程中压力诱导纳米柱子中的空位浓度梯度会导致物质输运, 使得纳米柱持续生长. 基于上述机制, 容易获得恒定压力下具有线性空位浓度分布的纳米柱子的生长方程为 (Liu et al. 2019)

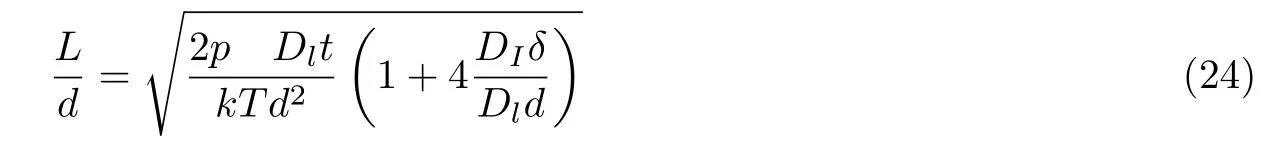
其中Dl和DI分别为体扩散系数和金属与模具界面扩散系数,δ为界面层厚度,k为波尔兹曼常数. 式(24) 表明扩散输运主导的纳米柱的生长将导致纳米柱的长径比随着其直径的减小而增加,这可以很好的解释实验观察 (图16 中红色数据点) (Liu et al. 2019).

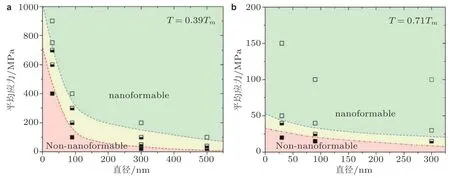
图 15 纳米模铸Au 过程中临界成型压力与孔道尺寸的关系(Liu 2019).(a)成型温度为0.39Tm,(b)成型温度为0.71Tm

图 16 晶态和非晶态金属在纳米模铸过程的尺寸效应(Liu et al.2019),成型能力通过L/d 反映.图中黑色实心方块和红色五边形点分别为金属玻璃(Shao et al.2013)和块体Au(Liu et al.2019)的纳米成型实验结果,品红色实线和蓝色实线分别为考虑表面张力(γ = 1 N/m,θ = 120°)(Williams et al.2008)和不考虑表面张力作用的Hagen−Poiseuille 理论预测.块体Au 的纳米模铸条件为在622℃和约800 MPa 下成型100 s.对于金属玻璃,理论(品红色实线)和实验结果(黑色实心方块)的偏差源于纳米尺度下黏度的显著增强(Shao et al.2013)

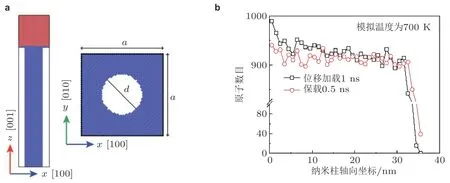
图 17 纳米模铸块体Au 的分子动力学模拟,模具材料为单晶硅.(a)模型图,左边为侧视图,右边为模具的俯视图;(b)位移加载1 ns 时(黑色点划线)和位移载荷保持0.5 ns 后(红色点划线)Au 原子数目沿着纳米柱轴线的分布

需要指出的是, 式 (24) 所预测的尺寸越小, 模铸越容易的现象仅在纳米尺度下有效. 一方面,随着尺寸的增大, 柱子的比表面积显著降低, 因此界面扩散的贡献相比体扩散可以忽略; 另一方面, 当柱子尺寸大于1 μm 时, 体扩散导致的生长速率将小于1 pm/s (图18) .

由于金属材料在高温下具有可比拟的扩散系数, 可以预测各种金属在扩散主导的温度区间都能通过纳米模铸实现表面纳米化. 典型的实验结果如图19 所示, 各种纯金属、固溶体、有序相都能通过高温纳米模铸快速实现表面纳米化.

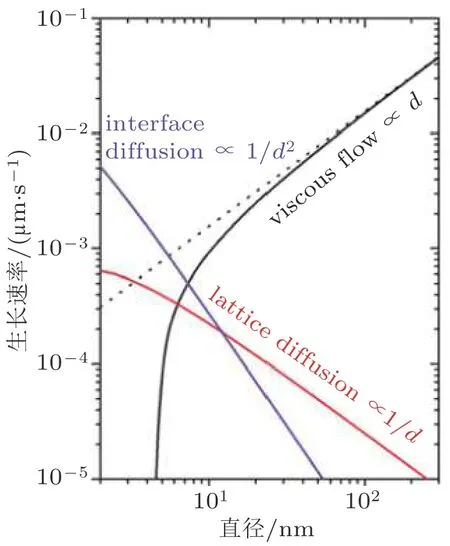
图 18 对比纳米成型过程中不同变形机制导致的纳米柱的生长速率(Liu et al.2019).图中扩散主导的变形机制是根据Au 在500 ℃下的参数计算得到(对式(24)求导数),体扩散和界面扩散分别对应图中红色和紫色曲线).作为对比,基于黏性流动的Pt57.5Cu14.7Ni5.3P22.5 金属玻璃纳米柱子的生长速率如图中黑色线条所示(式(18),成型压力取为500 MPa,纳米柱的长径比取为5)

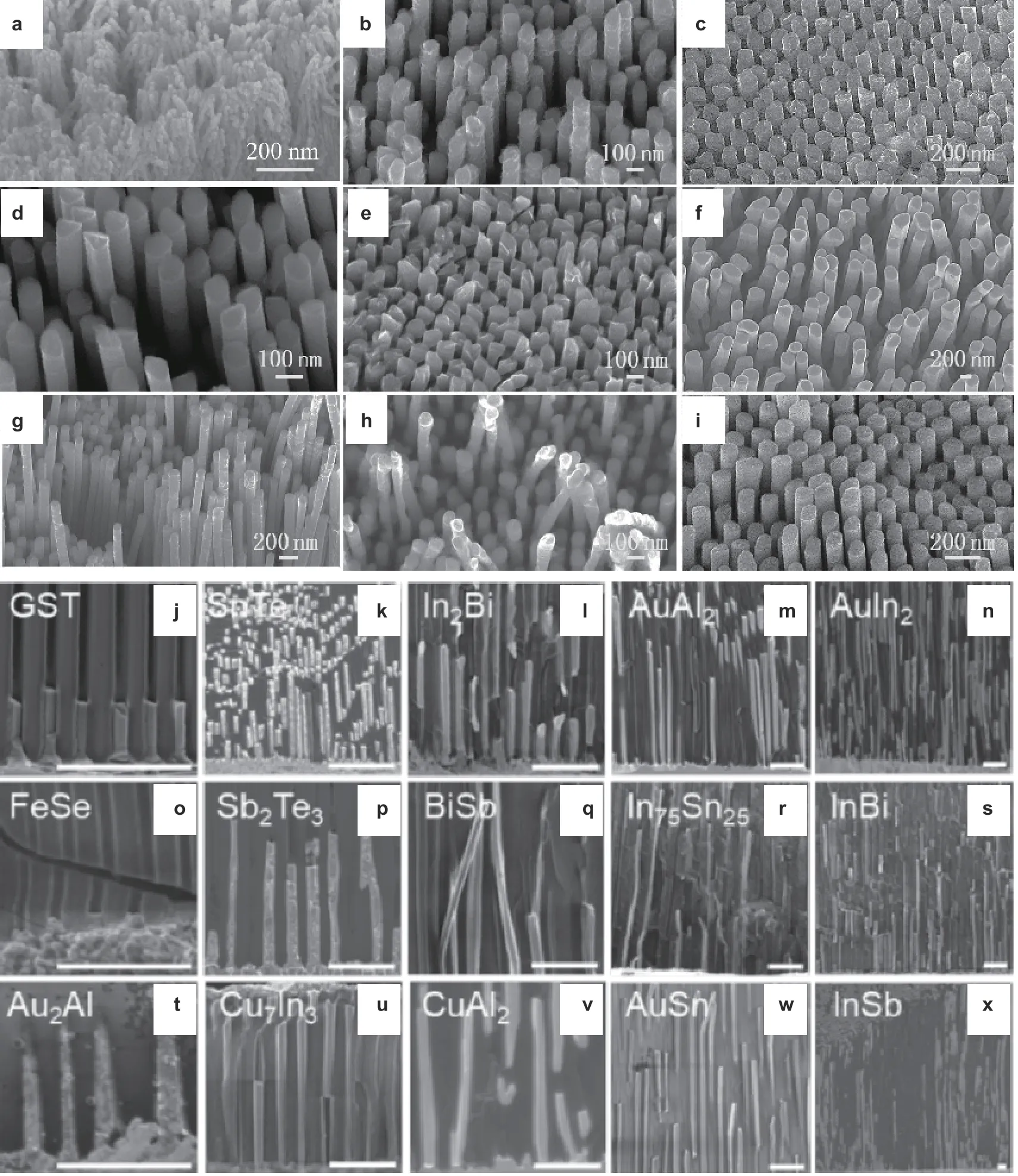
图 19 应用超塑性纳米模铸制备各种纳米柱阵列(Liu et al.2020,2019).(a)直径为5 ~ 13 nm 的金纳米柱(面心立方);(b)镍(面心立方);(c)钒(体心立方);(d)铁(体心立方);(e)Ni60Ti40(形状记忆合金);(f)Ag75Ge25;(g)Cu34.7Zn3.0Sn62.3(形状记忆合金);(h)PdCuNi;(i)PdCuNiPtRhIr(高熵合金);(j)~(x)各种功能材料纳米线(比例尺为1 μm),包含: Ge2Sb2Te5(GST,相变材料),FeSe(超导体),Au2Al(有序相),SnTe(拓扑绝缘体),Sb2Te3(拓扑绝缘体),Cu7In3,In2Bi,BiSb(拓扑绝缘体),CuAl2,AuAl2(彩色材料),In75Sn25(电子焊料),AuSn,AuIn2(超导体),InBi 和InSb(半导体).

5 小结和展望

自基于聚合物材料的软光刻技术发明以来, 成型技术开始进入到纳米尺度, 尤其是近年来实现了非晶合金、晶体金属、固溶体和有序相的纳米模铸, 使得低成本、高效率制备各种材料表面纳米结构成为可能, 这将极大促进纳米材料的广泛应用. 然而, 尽管纳米成型技术取得了上述突破, 并且相应的材料变形机理也取得了可喜的进展, 但微纳成型领域仍然存在较大的挑战, 以下列举一些具体的技术挑战与关键的力学问题:

(1) 纳米压印或纳米模铸技术都显著依赖于模板, 由于受到模板材料与脱模技术的限制, 对一些活性材料, 虽然能够进行纳米模铸, 但制备的纳米材料与模板存在分离困难的挑战. 因此, 非常有必要开发机械脱模技术, 并从理论上建立脱模过程的力学模型, 这不仅能够丰富JKR 接触理论, 同时也可以促成纳米模具的重复使用从而降低成本.

(2) 目前常使用的纳米模具或是基于光刻技术制备, 或是基于阳极氧化铝模板, 模板的制备技术决定了上述纳米模板通常为平面结构, 因此通过微纳成型制备复杂构型三维纳米结构还存在挑战.

(3) 随着特征尺寸的降低, 比表面积显著增大, 可以预见由于界面摩擦力的存在, 基于模板的微纳成型技术在制备大长径比纳米结构时会存在效率问题. 因此, 改善或开发新的微纳成型技术是关键. 最近, 作者课题组发现在纳米模铸过程中叠加微幅低频振动可以有效提高成型效率(Zhang et al. 2021), Ge 等(2021)应用超声振动加载, 也实现了室温下部分金属的纳米模铸. 然而,对于振动促进成型的微观物理过程及力学机理, 目前还不是很清楚.

(4) 随着成型技术进入到微纳米尺度, 表面粗糙度由于不满足尺缩规律, 因此在微纳成型过程中将造成局部接触状态的差异, 导致制备的纳米结构虽然短程有序, 但长程通常会存在缺陷,因此如何从原理和技术上保证微纳成型工艺制备微纳结构的均匀性, 还需要细致深入的研究.

(5) 对块体晶体进行微纳米成型, 由于此时模具尺寸通常小于晶粒尺寸, 因此需要考虑材料各向异性对成型过程中纳米晶生长的影响; 此外, 在较高温度下由于晶界处高的扩散活性还需研究晶界对成型过程中材料变形的影响.

(6) 结合合金化技术及微纳成型技术, 有望在微纳米尺度下对纳米结构的尺寸和组分同时进行调控，这不仅可以显著改善材料的力学性能 (曲绍兴和周昊飞 2014), 还能实现多功能纳米材料的一体化设计与制备.