基于微观结构非均匀性的非晶合金力学行为

乔吉超 张浪渟 童 钰 吕国建 郝 奇 陶 凯

西北工业大学力学与土木建筑学院, 西安 710072

1 引 言

非晶合金是合金熔体在急冷过程中形成的一种新型金属材料, 其微观结构长程无序而短程有序. 非晶合金兼具金属和玻璃特性, 表现出独特的力学、化学和物理性能, 如高强度、高断裂韧性、高弹性应变极限、耐腐蚀、优良的软磁性能及在过冷液相区具有超塑性等, 在材料科学和工程应用领域中具有巨大潜力而备受关注 (Hufnagel et al. 2016; Inoue & Takeuchi 2011; Johnson 1986, 1999; Qiao et al. 2019b; Wagner et al. 2011; Wang W H 2012, 2019).

玻璃作为一种古老的材料, 人们对其认识还远远不够, 玻璃态本质是凝聚态物理和材料科学中的一个难题. 非晶合金结构类似于硬球堆积, 被认为是结构最简单的玻璃体系, 可作为研究弛豫机制和玻璃转变行为的理想模型, 同时非晶合金的诞生也带来了许多未解决的问题和挑战. 非晶合金的微观结构是非均匀的, 难以利用传统分析方法进行表征 (Tao et al. 2021, Xu et al. 2020,Zhang et al. 2018, 管鹏飞等 2017). 由此, 非晶合金的力学性能与微观结构的本征关联是个仍未解决的重要科学问题 (Johnson 1986; Liu et al. 2011; Qiao et al. 2019b, 2016b; Wang W H 2019; Zhu et al. 2021). 单纯研究某种或几种因素并不能有效描述非晶合金微观结构非均匀性与力学行为的关联. 探索非晶合金的结构本质需综合诸多因素, 在不同时空激励下研究非晶合金微观结构非均匀性与变形机制, 并探明不同空间尺度结构特征及其演化规律. 本文将基于多尺度时空下的力学激励, 讨论非晶合金微观结构非均匀性特征与演化规律, 从实验、理论和数值模拟角度出发, 从原子扩散与其相应的宏观力学响应等方面阐明非晶合金微观结构非均匀性与力学行为之间的关联. 本综述拟探讨的核心科学问题为“多尺度时空力学激励下, 非晶合金的微观结构非均匀性-力学行为关联”, 属于固体力学领域前沿热点问题. 本综述以期为非晶合金的性能-结构关系提供崭新视角, 主要目的在于增进对非晶合金变形机理的理解 (Afonin et al. 2019; Monnier et al. 2020;Qiao et al. 2018; Wang W H 2019; Yang et al. 2020; Yu et al. 2017, 2012).

图1 为本文框架布局示意图. 第1 部分为绪论, 在此概述“非晶合金结构非均匀性-力学行为”之间关联的重要意义; 第2 部分概述了非晶合金微观结构的实验表征和分子动力学模拟; 第3 部分回顾了基于结构非均匀性发展的力学-物理模型; 第4 部分为非晶合金的动力学弛豫行为和力学性能之间的关联; 第5 部分为非晶合金黏弹性变形与微观结构非均匀性的研究进展; 第6 部分为非晶合金微观结构非均匀性的力学调控方法; 最后在第7 部分进行总结与展望.

2 微观结构非均匀性

非晶合金原子排列长程无序, 在宏观上体现为均匀和各向同性. 然而由于其与晶体具有相同的原子化学键, 两者具有相似的短程序结构图像. 短程序(约0.5 nm) 和中程序(0.5 ~ 1 nm) 所体现的结构非均匀性是非晶合金的本质特征, 是塑性变形和弛豫的结构起源(Ding et al. 2014a, Elliott 1991, Liu et al. 2011, Peng et al. 2011). 结构非均匀性与非晶合金力学及其动力学响应密切相关, 不断探索和了解结构非均匀性对理解和调控非晶合金力学性能至关重要. 随着实验技术和模拟手段的发展, 非晶合金微观结构非均匀性可通过多种手段研究, 如X 射线和中子衍射 (Kelton et al. 2003)、高分辨率透射电子显微镜 (Zhong et al. 2014) 、动态原子力显微镜 (Yang et al. 2012) 、纳米束电子衍射 (Nomoto et al. 2021) 、原子电子断层扫描 (Yang et al. 2021)和分子动力学模拟 (Cheng & Ma 2011, Tang & Harrowell 2013)等.

图 1 本文框架示意图

2.1 微观结构非均匀性表征

香港城市大学杨勇课题组(Ye et al. 2010)通过动态微柱实验表征了表观弹性区域内非晶合金的非弹性变形, 发现排列松散自由体积区域被排列紧密弹性外壳所包裹, 具有类似过冷液体特征. Wagner 等(2011)利用原子力声学显微镜, 观察到 PdCuSi 非晶合金纳米尺度上局部压痕模量遵循高斯分布, 晶化样品局部模量差异大大降低, 表明非晶合金存在微观结构非均匀性现象.此外, 陈明伟等从非晶合金表面局域能量耗散和模量变化角度, 利用振幅可调节动态原子力显微镜, 从实验中直接观察到能量耗散与模量非均匀, 尺度约为2.5 nm (Liu et al. 2011, Zhu et al.2018). 为揭示非晶合金微纳米结构弹性非均匀性, Tsai 等(2017)提供了一种基于纳米压痕动态模量映射方法来检验模量随空间位置的分布. 动态模量成像(dynamic modulus mapping)方法将扫描探针与动态力学分析相结合, 以绘制目标区域压痕获得模量信息 (Liu et al. 2011). 图2 中局部弹性特性的空间波动均清晰可见, 形成“弹性微结构”, 局部较硬区域和较软区域互相穿插, 其特征尺度约为100 nm (Tsai et al. 2017). Zhu 等(2018)通过纳米压痕方法建立了硬度与结构非均匀性之间的关联. 如图3(a), 随退火时间延长(非均匀性特征长度减小), 压入深度更小. 超淬火态样品硬度H, 杨氏模量E和非均匀性特征长度ξ之间近似服从幂律关系 (图3(b)). 此外, 在超淬火样品的压痕周围无明显剪切带, 而在高度弛豫态样品压痕周围出现明显的剪切带(图3(c)(d)).随结构非均匀性程度降低, 变形模式从均匀流变转变为高度局域化变形 (Li et al. 2019; Wang et al.2016).

图 2 均值聚类分析表征弹性微观结构非均匀性.(a)~(c)模量图的示例三色表示,其中像素根据模量(蓝色为软区,绿色为中间区,黄色为硬区)分组,图像(a)表示铸态样品的中心位置,(b)为样品退火后的中心位置,(c)180 W 激光脉冲处理的样品;(d)~(f)反卷积直方图,显示了三种结构分布(Tsai et al.2017)

最近, Yang 等(2021)利用原子电子断层扫描技术观测到非晶固体中的三维原子结构, 在单原子水平定量分析了多组分玻璃形成纳米颗粒中的短程序和中程序结构. 部分短程有序结构相互连接形成中程序, 该观察结果支持了非晶合金有效团簇堆积模型的一般框架. 非晶固体中程序在体积上与塑性变形的基本单元-剪切转变区相近, 因此原子电子断层扫描技术有望用于确定与剪切转变区相关的三维原子结构, 从微观原子结构方面理解非弹性变形机理(图4).

2.2 原子尺度结构与动力学非均匀性

尽管通过先进的实验技术可以间接确认非晶合金的微观结构非均匀性特征, 然而如何在原子尺度上对非晶合金结构非均匀性进行深入细致的理解并建立可靠的几何拓扑结构模型仍是当前面临的巨大挑战. 近年来大量基于分子动力学模拟的相关工作试图从原子尺度上揭示非晶合金的结构非均匀性特征, 以期建立微观非均匀性结构与宏观力学行为之间的关联 (Cheng & Ma 2011, Ma 2015).

图 3 (a)超淬火,部分弛豫和高度弛豫样品的纳米压痕力−深度曲线;(b)纳米压痕硬度和模量与结构非均匀性的特征长度关系;(c)超淬火样品和高度弛豫样品的压痕形貌(Zhu et al.2018)

非晶合金中包含了各种各样的原子短程序结构, 但学者们发现局域五次对称性即以五边形的面占主导的二十面体结构是普遍存在的, 这种结构在非晶合金玻璃转变、变形以及动力学行为等方面起重要作用 (Cheng & Ma 2011). 如图5 所示, Cu64Zr36合金液体在冷却过程中二十面体结构含量急剧增加, 与此同时大部分其他类型的多面体结构含量随之降低 (Cheng et al. 2009). 研究表明非晶合金的微观结构对不同类型的多面体结构具有不同的程度的偏好. 对于Cu64Zr36非晶合金体系, 以Cu-〈0,0,12,0〉为中心原子的二十面体结构明显优于其他类型的多面体结构, 表现出结构稳定、排列紧密的局域结构, 具有较高的模量和抗剪切能力. 相反, 其他大部分类型的多面体结构团簇则排列较为松散, 具有较大的原子移动性 (Feng et al. 2016).

非晶合金中存在不同构型的短程序结构, 其微观尺度表现出密度、模量以及能量等的不均匀分布. Feng 等(2016)采用分子动力学模拟研究CuZr 非晶合金的结构演化, 如图6 所示, 发现在1%的压缩应变下CuZr 非晶合金中的原子具有不同的原子局域应变. 模拟结果与实验结果相互吻合, 证实Cu64Zr36非晶合金是由排列密集的原子团簇以及其周围包裹着的排列松散的相连区域所组成. 微观结构上的不均匀性, 即同时存在“类固区”和“类液区”, 使得非晶合金在力学性质上具有显著的空间涨落. 王云江等(2020)通过计算黏滞流动激活能结合过渡态理论计算CuZr非晶合金黏度的空间分布, 图7 所示CuZr 非晶合金的黏度空间分布表现出显著的空间涨落. 由黏度空间分布的涨落特点也证实了非晶合金中存在“类固区”和“类液区”.

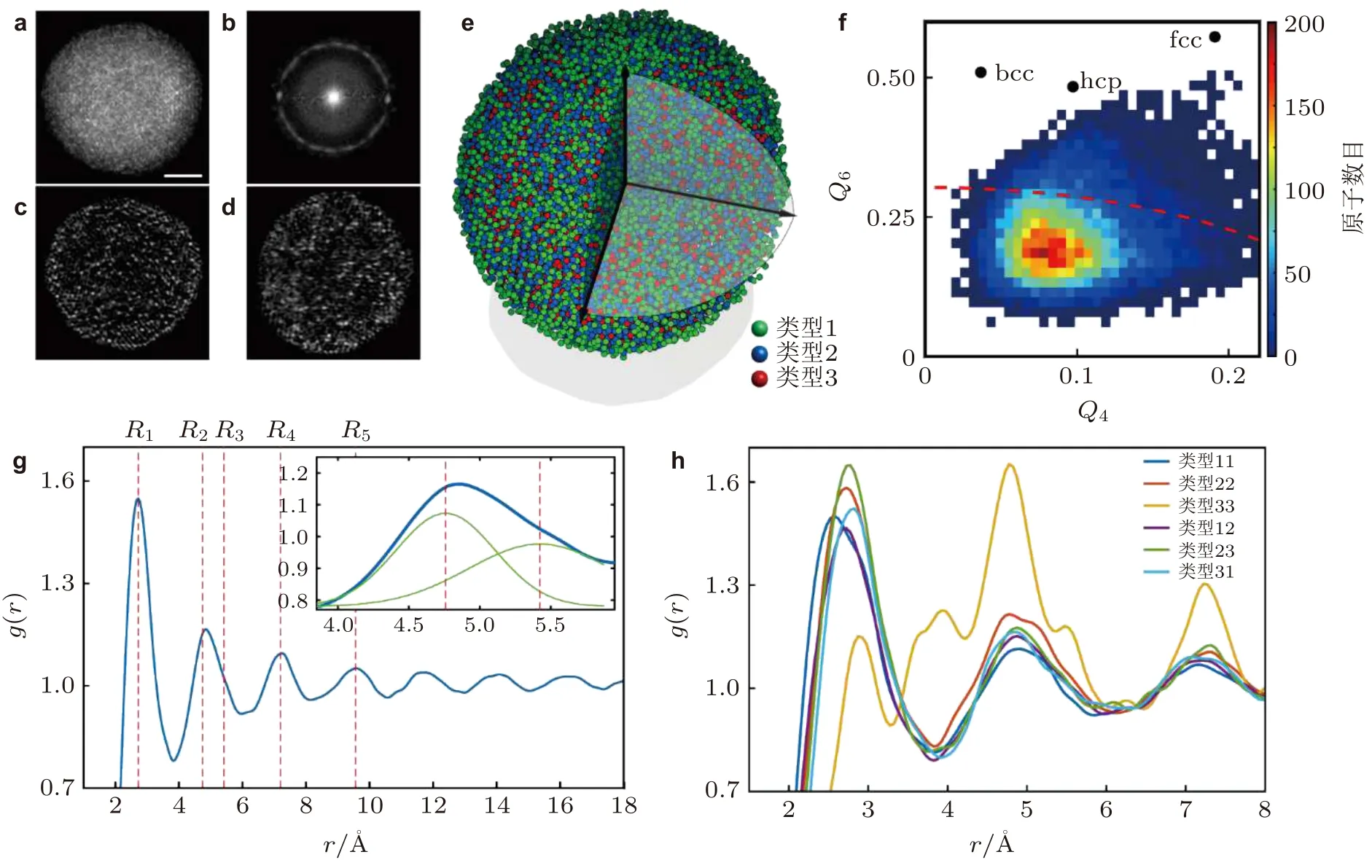
图 4 利用原子电子断层扫描技术观测到非晶固体中的三维原子结构,1 Å = 0.1 nm(Yang et al.2021)

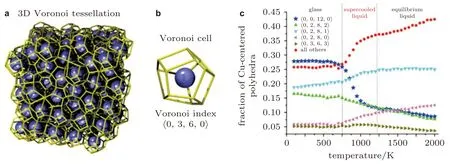
图 5 (a)Voronoi 多面体结构,(b)中心原子的Voronoi 指数(Cheng &Ma 2011),(c)Cu64Zr36 非晶合金中以Cu 原子为中心的多面体含量随温度的演变(Cheng et al.2009)

图 6 CuZr 非晶合金在分子动力学模拟和实验中的结构特征.(a)压应变为1%时的原子应变分布,(b)图(a)中的局域结构放大图,(c)高分辨透射电镜下的显微结构,(d)密度分布图(Feng et al.2016)

图 7 典型CuZr 非晶合金黏度空间分布(王云江等2020)

体系的动力学信息与其所处能量状态以及能垒变化紧密关联. 势能图谱(potential energy landscape, PEL)可提供原子扩散信息, 通过激活能垒大小可有效表征局域原子被激活的难易程度. 强液体的PEL 存在大能谷, 而弱液体较为复杂, 其PEL 由多个不同大小的能谷组合而成, 表明弱液体相对于强液体具有更不均匀的微观结构和动力学特征 (Debenedetti & Stillinger 2001).由于PEL 是复杂的高维平面, 因此准确获得非晶合金的PEL 信息是极其困难的. 针对这一难题,Barkema 和 Mousseau (1996)开发并改进的ART(activation-relaxation technique)算法通过对鞍点态进行随机抽样来得到非晶合金体系中不同事件的激活能. 图8 给出了Cu50Zr50非晶合金激活能的空间分布特点, 在三维空间中展现出众多大小不同的峰值和谷值. 原子激活能分布在0 ~ 5 eV的范围, 呈现出较为宽广的分布. 这些结果均表现出非晶合金PEL 的复杂性以及非均匀分布特点 (Wei et al. 2019). 激活能分布谱可进一步分为两种模式, 一种是处于较低激活能的指数衰减模式, 另一种则是处于中等到较大激活能范围的Rayleigh 模式. 前者类似于具有级联过程的液体动力学特征, 而后者则对应于固态结构, 其激活行为类似于局域化过程 (Fan et al. 2014, 2017).

图 8 (a)Cu50Zr50 非晶合金的局域事件激活能的空间分布特点,(b)体系中某个Zr 原子沿不同方向激活1000 次的激活能分布,(c)~(e)体系中原子的激活能分布谱(Wei et al.2019)

3 基于微观非均匀结构的力学/物理模型

非晶合金结构由“类固区”和“类液区”等不同区域组成, 外加应力激励下类固区的响应由弹性主导, 类液区的响应是非弹性的 (Liu et al. 2011). 非晶合金的宏观变形行为可视为微观局部变形的聚集, 从局部变形到宏观变形的过程是认识其变形和失稳的关键 (汪卫华 2013). 为进一步理解非晶合金微观尺度变形机制, 本节将主要介绍基于微观非均匀结构建立的与非晶合金变形相关的的理论模型.

3.1 自由体积模型

Cohen 和Turnbull 建立自由体积模型用于解释玻璃转变与液体的扩散输运现象 (Cohen &Turnbull 1959, Turnbull & Cohen 1970). 固体和液体总宏观体积包含原子/分子的实际占有体积和自由体积, 自由体积可理解为原子周围的空隙以大小不等的空穴无规分散在基体中, 可在能量等构型状态下重新分配. 玻璃转变温度以下微观结构被冻结, 空穴尺寸和分布基本不变, 此时密度随温度升高而线性降低. 玻璃转变温度之上非晶合金随温度升高发生的膨胀包括固有体积膨胀和自由体积膨胀. 类似于晶体中的空位, 非晶合金中特定的原子重排也需要临界自由体积. 自由体积模型体现了非晶态物质微观结构非均匀性, 由于原子无序排布, 每个微区域所具有的自由体积大小并不相同, 服从一定的统计分布, 进一步导致了原子跃迁激活能的统计分布.

Spaepen (Spaepen 1977, Spaepen & Turnbull 1974) 在Turnbull 和 Cohen (1970)工作基础上对非晶合金原子扩散和塑性剪切流动行为进行解释, 以自由体积为序参量, 计算了非晶合金均匀流动和非均匀流动的边界及流动方程, 揭示了稳态流动的微观机制是基于应力驱动缺陷产生与扩散导致缺陷湮灭之间的动态平衡. 如图9, 原子跃迁前提为周围空穴大小在临界自由体积之上.无外力场作用时原子跃迁在不同方向上几率相同, 而外力场作用下原子跃迁倾向于剪切应力作用方向, 导致原子运动具备方向性, 跃迁需要邻近自由体积存在和激活能两个条件. 原子跃迁导致的微观变形与宏观变形之间通过原子跃迁分数Δf进行关联, 均匀流动原子跃迁分数Δfh为1,而非均匀流动Δfi约为10-6. Zhu 等(2021)将体系内物质点自由能看做局部应变状态和局部原子浓度(自由体积)的函数, 根据热力学定律建立了非晶合金塑性随时间演化的连续介质模型, 该模型成功描述了非晶合金蠕变过程中临界应力附近蠕变速率和应力关系的两个不同的幂律转变过程.

图 9 非晶合金中单原子扩散跃迁过程示意图(卢博斯基 1989)

3.2 剪切转变模型

Argon 等(1979)认为非晶合金变形基本单元是能容纳剪切应变的局部原子重排, 可具体描述为变形基本单元由自由体积位点及其周围环境构成. 在热力耦合作用下, 应变通过自由体积位点形核的剪切转变 (shear transformation, STs) 导致, 如图10 所示. 变形局域化的重要原因是剪胀效应, 在剪切转变过程中, 由周围原子被推开而产生的膨胀分量在通过扩散重排湮灭前会存在一定时间, 反馈为加速了剪切局域化过程. 剪切转变作为当前最为人所接受的非晶合金变形理论, 对其他玻璃态物质也有广泛适用性 (Hutnik et al. 1993). 近年来, 随着非晶合金的广泛研究,对STs 作为塑性载体的观点日益被研究者所重视, 下面介绍该理论的重要发展:

图 10 非晶合金中二维剪切转变区示意图(Argon 1979)

图 11 非晶态物质在准点缺陷理论框架下的微观变形描述.(a)初始结构,(b)~(d)为热力耦合激励作用下的激活、扩展和融合行为(Rinaldi et al.2011)

(1) Falk 和Langer (1998)基于Argon (1979), Spaepen 等 (1974)的观点, 提出了剪切转变区(shear transformation zone, STZ)理论, 该理论旨在成为自由体积模型、剪切转变理论等流动缺陷理论的补充和延伸. 此处简要介绍两者的区别: ① Argon (1979)认为STs 不是非晶态固体中的结构缺陷特征, 并非预先存在, 而是原子团簇在局部剪应力作用下发生复杂结构弛豫的产物.Falk 和Langer 在黏塑性变形的分子动力学模拟工作中引入的STZ, 是结构中已经存在的缺陷区域, 在外加应力下在两种结构状态间的转变产生变形增量. ② Argon (1979)认为剪切转变前后的原子团簇均是随机密堆积, 因而有相似的原子排列结构, 表明已经发生剪切转变的区域可以再次发生剪切转变而承载变形. 然而, 根据Falk 和Langer 的描述, STZ 大多是具有两种稳定构型的原子团簇, 其通过在两种构型间的来回转变产生剪切变形增量, 因而一个已经发生剪切转变的区域无法在同一方向上再次转变.

(2) 由于对非晶合金断裂实验中, 拉伸正断, 纳米周期条痕结构等断裂特征的观察, 中国科学院力学研究所戴兰宏课题组认为非晶合金脆性断裂的微观机制是准脆性的纳米尺度孔洞化, 进而提出了体胀主控的“拉伸转变区 (tension transformation zone, TTZ) ”模型 (Jiang et al. 2008, 蒋敏强 2017). 通常认为STZ 事件是剪切应力主控的, 伴随的体胀变形非常微弱(小于剪切效应2 ~3 个量级). TTZ 对应于STZ 事件的极端情形, 即静水拉应力驱动的体胀主控, 此时非晶合金膨胀为主, 而剪切变形相对微弱. 此时一系列TTZ 事件将导致纳米孔洞化, 能量通过新表面的形成而耗散, 导致脆性断裂. 可以预期, TTZ 的激活应当满足两个条件: ① STZ 事件没有足够的时间激活而处于相对劣势, 此时剪应力分量相对小; ② 局部应力的静水应力分量大小达到孔洞成核的临界应力. 此外, 微观上局部原子团簇运动应当与应变速率、温度和应力等条件相关, 运动模式存在剪切主控(STZ)向体胀主控(TTZ) 的过渡, 这与非晶合金的韧脆转变现象密切相关 (Jiang et al. 2010).

3.3 准点缺陷理论

为了描述非晶合金动态弛豫行为、变形行为随微观结构的演化, Gauthier et al. (1997)和Perez (1990)等提出准点缺陷模型(quasi-points defect, QPD), 将宏观力学行为与原子/分子运动联系起来. 该理论有三个基本假设: (1) 非晶态物质在纳米尺度上存在对应焓和熵等起伏的密度波动, 定义为准点缺陷; (2) 非晶态物质内部原子/分子运动分级关联, 最易运动的原子/分子被激活后引起更复杂的原子/分子运动; (3) 外加力场作用下, 微剪切畴发生激活、扩展和合并. 与整个材料平均涨落相比, 图11(a)所示的准点缺陷位点处密度、焓和熵等参量变化更大, 能量状态高, 因此原子/分子重排优先在准点缺陷位点处发生, 如图11(b)中最大剪应力面上的缺陷部位激活. 激活过程中, 一定数目的原子发生构型变化, 产生局部剪切变形原子排列构型优先发生. 在外加应力持续作用下, 微剪切畴(shear microdomain, SMD)在激活准点缺陷位点成核长大(图11(c)). 微剪切畴长大对应于滞弹性变形, 应力卸载时微剪切畴收缩, 滞弹性变形逐渐回复.微剪切畴无法无限长大, 这是因为应力长时间作用下, 相邻微剪切畴边界相互融合(合并), 其边界弹性能释放, 产生塑性变形 (图11(d)).

3.4 流变单元模型

流变单元模型由中科院物理研究所汪卫华研究团队(Wang & Wang 2019, 王峥 2013)提出,将非晶合金结构视作弹性基底上嵌入流变单元, 与弹性基底相比, 流变单元弹性模量和硬度更低, 具有更快的动力学特征. 图12 为非晶合金中流变单元低温时空间分布, 流变单元模型将纳米级软区或流变单元嵌入非晶合金基体之中. 流变单元中的原子键合较弱、堆积密度更低, 弹性模量更低, 原子移动性高, 在剪切应力作用或热激活下易被激活, 发生原子迁移.

图 12 高能量状态流变单元示意图(Wang &Wang 2019)

3.5 理论模型之间的异同讨论

自由体积模型使用简单清晰的物理图像解释了非晶合金玻璃转变和流变行为. 而单原子跃迁过于简化, 无法描述非晶合金实际变形中涉及大量原子簇协同运动过程 (Schall et al. 2007). 此外非晶合金中自由体积浓度约2%, 仅在自由体积处发生原子跃迁与实际不符 (Egami et al.2013). “剪切转变区”相关概念可以再现宏观应力-应变关系, 解释导致剪切带形成的应变局域化发生的结构起源. 此外, 理论认为STZ 并非结构缺陷, 其仅在力热耦合刺激使其激活后才能进行识别, 无法反映非晶合金内部的固有非均匀微观结构. 准点缺陷理论从统计物理角度给出了非晶合金内部的缺陷形式, 不仅可帮人们理解结构非均匀性与动力学非均匀性, 而且考虑准点缺陷激活形成“剪切微畴”, 以及剪切微畴的扩展、融合, 可以厘清力热耦合刺激作用下非晶合金弹性、滞弹性和塑性应变响应. 然而, 准点缺陷理论仅给出了非晶合金高温、低应力作用下的均匀变形过程中的力学行为. 而非晶合金在低温、高应力作用下应变高度局域化, 剪切带形成后扩展断裂过程无法使用该理论进行描述.

对比以上理论, 可发现剪切转变区、剪切微区域和流变单元等均可以理解为具有较高原子移动能力、在外加激励下优先发生协同重排运动的原子团簇. 流变单元的激发、演化等过程可看做类液的流变单元相在弹性基体上的形核与长大. 变形初期, 内部原子变形可视作可逆的滞弹性变形, 受到外层弹性边界的束缚, 卸载应力后变形逐渐回复. 非晶合金宏观失稳是由微观的局域失稳过程聚集和发展而成, 由于微观尺度的原位局域化变形实验还难以直接观察, 变形过程尚不明晰, 建立非晶合金的形变机制和物理模型仍是非晶领域的核心问题之一.

4 动力学弛豫与微观结构非均匀性的关联

动力学弛豫(dynamic mechanical relaxation)是材料在交变应力作用下由分子、原子等原因产生非弹性应变, 该应变达到平衡需要一定时间, 使宏观应变滞后于应力并伴随能量耗散 (Wang W H 2019). 非晶合金弛豫时间分布范围较广(10-14~ 106s), 在外力激励下表现出不同形式 (Yu et al. 2010). 研究非晶合金弛豫行为有助于深入理解其结构特征及形变机制和玻璃转变等众多行为的物理本质. 图13 为宽频率域内的高分子玻璃介电损耗谱(Lunkenheimer et al. 2005). 在频率域内高分子玻璃表现出多种弛豫过程, 首先观察到的是对应玻璃转变行为的主弛豫(α 弛豫), 较高频率域(102~ 109Hz 频率域)出现独立的弛豫过程称为慢β 弛豫; 在1012Hz 观察到玻色峰.

图 13 在极宽频率域内测得高分子玻璃中的介电损耗谱(弛豫现象)(Lunkenheimer et al.2000)

4.1 主弛豫−α 弛豫

α 弛豫对应于大范围原子协同重排运动并偏离弛豫时间对温度的Arrhenius 依赖关系 (Dixon et al. 1990). 频域内非晶合金损耗模量主曲线可由扩展指数方程表示为 (Bergman 2000):,Gp为归一化后损耗模量峰值;Gu为未弛豫模量;ωp为主弛豫对应峰值频率, 扩展指数βKWW与特征时间分布宽度相关, 可作为衡量非晶合金微观结构非均匀程度的标尺之一. 基于“准点缺陷”理论, 损耗模量随频率演化可表达为(Perez 1990):G∗(iω)=Gu/G∗为复模量; λ 为拟合常数; χ 为关联因子,介于0 和1 之间. 关联因子χ 对应非晶态物质的“准点缺陷”浓度. χ = 0 代表结构完全有序, 变形单元运动受所有其他单元运动影响; χ = 1 代表结构完全无序, 变形单元运动相互独立. 图14(a)为扩展指数方程对非晶合金主弛豫的拟合结果, 扩展指数方程可以较好地描述非晶合金主弛豫行为, 玻璃转变温度以上βKWW随温度升高变大, 表明非晶合金非均匀程度降低 (Pelletier et al.2011). 主弛豫主曲线的拟合结果βKWW≈ 0.5, 这已被证实是非晶合金的固有特征之一 (Qiao &Pelletier 2012, Wang et al. 2008). 采用QPD 理论同样可对非晶合金损耗模量随频率演化进行描述(图14(b)), 关联因子χ 值增大表明在过冷液相区内原子移动性随温度升高而显著提高(图14(c))(Cheng et al. 2021).

4.2 次级弛豫−慢β弛豫

慢β 弛豫是非晶合金的本征行为, 同时也是α 弛豫的前驱 (Johari and Goldstein 1970; Ngai et al. 2013; Zhao et al. 2016). 非晶合金体系均具有明显的α 弛豫, 而β 弛豫在不同体系中表现出多样化模式 (图15(a)) (Yu et al. 2013): La 基体系表现出明显的慢β 弛豫(peak); Pd 基体系通常表现为肩膀峰(shoulder); 而对CuZr 基非晶合金而言, 其β 弛豫往往很难被直接观测到, 表现为α 弛豫峰上的过剩尾(excess wing). β 弛豫依赖于非晶合金热历史、外加应力以及热力学和动力学形成路径 (Casalini & Roland 2009, Lunkenheimer et al. 2005). 冷却速率越大, 非晶合金“缺陷”浓度越高, β 弛豫强度也就越高(图15(b)). 低于玻璃转变温度的物理老化(physical aging)导致β 弛豫峰移动至更高温度表明β 弛豫激活能增大, 意味着非晶合金微观结构非均匀程度可通过改变结构能量状态进行调控(图15(c)) (Zhang et al. 2021b).

图 14 不同温度下Zr 基非晶合金损耗模量G''/Gu 随频率演化.(a)实线根据KWW 模型拟合,(b)实线根据QPD 模型拟合,(c)关联因子随温度的演化(Cheng et al.2021)

图 15 (a)典型非晶合金体系归一化损耗模量随温度的演化(Yu et al.2013),(b)不同初始状态La 基非晶合金损耗模量随温度的演化(Zhao et al.2014),(c)La 基铸态和弛豫态非晶合金内耗随温度的演化(Zhang et al.2021b)

非晶合金微观结构存在原子排布较为疏松或原子间结合较弱的区域, 模量、强度和黏度较低, 而能量状态和原子移动性较高 (Wang W H 2019). 低于玻璃转变温度的物理老化会削减这些区域, 导致微观结构非均匀程度降低. 如图16 所示, 相较于物理老化状态, 铸态表现出分布更广、特征尺度更大的接触共振频率. 接触共振频率正相关于弹性模量, 因此铸态非晶合金具有更不均匀的弹性模量分布 (Wang D P et al. 2019). 非晶合金α 弛豫需要克服更大能量势垒, 涉及大范围、不可逆原子运动; β 弛豫对应临近小能谷之间跃迁, 涉及可逆、局域原子流变, 这些小能谷在高能区非常密集. 势垒位形图中小能谷密度与非晶态材料体系能量状态密切相关. 在非均匀性程度较高的不稳定材料体系中小能谷的分布非常密集, 在较为稳定材料体系中小能谷的分布较为稀疏. 弹性模量较低的区域处“缺陷”高度集中并具有高能量态. 具有较低弹性模量和更多结构“缺陷”区域对应于更明显的β 弛豫, 因此, β 弛豫强度与分布宽度也可作为衡量非晶合金微观结构非均匀程度的标尺.此外，β 弛豫与α 弛豫之间的关联可以作为搭建不同动力学弛豫与力学行为之间的桥梁. 非晶合金β 弛豫和α 弛豫的耦合程度与其脆韧转变具有密切关联. 再者, Yu 等(2012)研究发现, 非晶合金β 弛豫激活与合金中最小构成原子的扩散激活能相等, 这一研究成果为进一步探明非晶合金β 弛豫起源提供了参考依据，从能量角度证明了β 弛豫与非晶合金的力学性能有密切联系.

图 16 结构非均匀性与β 弛豫关联示意图.(a)非晶合金(铸态)的接触共振频率云图,(b)接触共振频率在(a)的分布,(c)铸态玻璃能量势垒图,(d)小能谷跃迁积累为β 弛豫,(e)非晶合金(物理老化后)的接触共振频率云图,(f)接触共振频率在(e)中的分布,(g)退火后玻璃能量势垒图,(h)β 弛豫强度减少(Wang D P et al.2019)

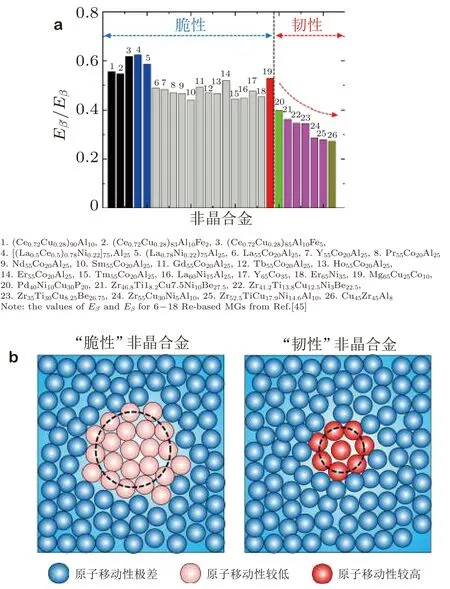
图 17 (a)典型非晶合金体系快β′弛豫与慢β 弛豫激活能之间的关系,(b)“脆性”非晶合金和“韧性”非晶合金微观原子排布示意图(Wang et al.2017)

4.3 快β′弛豫

王庆等(Wang et al. 2017, 2015a)首先发现一种La 基非晶合金在弛豫谱低温段呈现出动力学特征明显不同于β 弛豫的次级弛豫过程, 同时证实快二次弛豫-快β′弛豫普遍存在于非晶合金中. 当温度降低时, α 弛豫被冻结, 因此研究较低温度下(低于慢β 弛豫和α 弛豫解耦温度)非晶合金的动力学弛豫行为有助于理解快β′弛豫与慢β 弛豫的起源和关联. 非晶合金通常分为脆性和韧性两种, 快β′弛豫激活能和慢β 弛豫激活能的比值为非晶合金的分类提供了一种行之有效的方法(图17(a)). 相较于脆性非晶合金, 韧性非晶合金松散排列区域与周围弹性基底的原子移动能力存在更大的差异. 换言之, 脆性非晶合金往往比韧性非晶合金的微观结构更均匀 (图17(b)).从物理角度出发, β 弛豫起源于“链状”原子团簇构型激发运动, 类似于典型的随机局部STZ 激活,涉及一系列的“破笼”行为. “破笼”行为对应于小范围原子团簇重排运动或具有局部较高移动能力的镶嵌在弹性基底的“类液区”原子簇激活运动, 对应于快β′弛豫的激活 (Wang et al. 2015a). β弛豫与非晶合金的剪切转变区和屈服等相关, 涉及原子断键过程, 而快β′弛豫与非晶合金的滞弹性(anelasticity) 存在内在关联, 这种约束度更高的快β′弛豫过程对局域原子堆垛更为敏感. 这些发现有助于理解非晶合金微观结构不均匀性, 进而有助于系统建立并揭示非晶合金滞弹性变形、屈服至稳态塑性流变的物理本质.

4.4 玻色峰

非晶态物质和过冷液体在低拉曼散射或非弹性中子散射中观察到的低频动态特征称为玻色峰, 其性质是凝聚态物理学领域关注点之一. 晶体材料低频原子振动可通过格波来理解, 格波在长波近似下可视为连续介质弹性波, 振动模式密度(态密度)可通过德拜模型近似. 然而, 对于长程无序的非晶态物质, 其低频振动(太赫兹频率)总是偏离德拜模型预测而出现态密度过剩, 形成玻色峰. 这种反常现象意味着无序非晶体在玻色峰频率附近不可视为均匀的弹性介质, 在空间上是弹性无序的, 因此玻色峰与非晶合金微观结构非均匀性密切相关. 为了解释玻色峰的性质和起源, 学者们提出了许多理论模型, 如局域振动 (Elliott 1992), 弹性非均匀性 (Schirmacher et al.1998), 相变 (Grigera et al. 2003), van Hove 奇点 (Taraskin et al. 2001), Ioffe-Regel 极限 (Gurevich et al. 1993)等. 这些模型通常是基于松散排列的原子 (Tang et al. 2005)、低密度缺陷结构 (Tan et al. 2012)或中短程有序结构 (Sokolov et al. 1992)而建立的, 综合考虑了非晶态物质的无序结构. 近期理论研究和实验结果表明玻色峰与玻璃结构中“软模”有关, 这些“软模”在体系中呈现准局域分布, 激活能相对较低, 优先且易发生剪切转变. Yang 等(2019)采用Voronoi 多面体法寻找出玻色峰的方向序, 通过引入结构参数来描述方向顺序, 其空间分布解释了准局域模, 将非晶合金的玻色峰方向序的大小和强度相关联. Ding 等(2014b)找到了“软模”的结构特征, 将几何不利构型视为缺陷. 因此, 玻色峰与非晶合金的微观结构非均匀性之间存在关联 (Carini et al. 2013;Mitrofanov et al. 2014).

此外, 玻色峰的强度和位置变化与非晶合金的微观结构非均匀性及其演化密切相关 (Huang et al. 2014). 与β 弛豫相似, 玻色峰强度对非晶合金的能量状态十分敏感, 这意味着可以通过物理老化和年轻化来调控玻色峰的强度并探究不同弛豫机制之间的关联. 如图18(a)所示为不同能量状态下非晶合金在5 ~ 30 K 之间的热容, 剔除晶体热容贡献可分离出非晶合金的玻色峰(图18(b)), 增加退火温度可以显著降低玻色峰强度(能态较低), 而增大变形程度则可以有效增强玻色峰强度(能态较高) (Mitrofanov et al. 2014). 图19 所示为玻色峰与β 弛豫峰和α 弛豫峰之间的关联. 玻色峰与软区中原子或原子团簇的准局域振动有关, 对应于势能图谱中小能垒的状态跃迁, 温度升高时原子/团簇会小规模可逆移动, 构成β 弛豫, 即缺陷区域的局部流动 , 温度继续升高时弱黏结区周围的弹性矩阵变软并进行协同作用, 构成α 弛豫 (Huang et al. 2016). 玻色峰主要来源于随机致密的团簇堆积结构, 强烈依赖于非晶合金的结构状态, 可以通过谐波局域模式来解释 (Li et al. 2008). 高压扭转引入剧烈的塑性变形使非晶合金向高能状态跃迁, 玻色峰强度得到提高, 而高温物理时效诱导非晶合金向更稳定状态跃迁, 玻色峰强度降低, 玻色峰强度的变化被进一步证明是与剪切带区域内低频模的演化强相关 (Bünz et al. 2014).

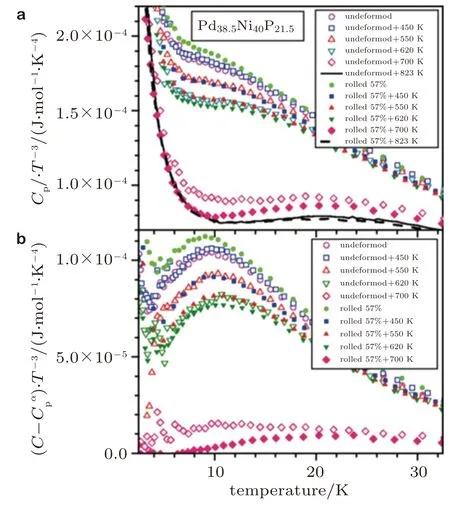
图 18 (a)不同状态下非晶合金热流随温度的演化,(b)剔除晶化影响后的热流随温度的演化(Mitrofanov et al.2014)

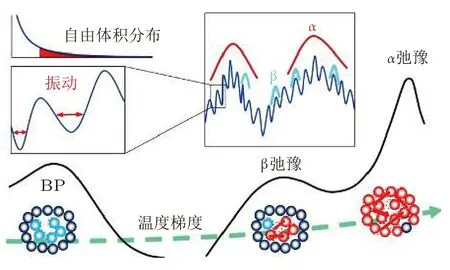
图 19 具有温度依赖性的动力学相关的自由体积分布(左上角).沿温度升高梯度,分别为玻色峰、β 弛豫峰和α 弛豫峰(Huang et al.2016)

图 20 (a)部分区域晶化的Pd42.5Ni7.5Cu30P20 非晶合金的高分辨电镜图(Ichitsubo et al.2005);(b)不同温度下La60Ni15Al25 非晶合金的应力松弛曲线,其中实线为KWW 拟合曲线(Wang et al.2014);(c)弛豫分布宽度相关指数βKWW随温度的演化(Wang et al.2014);(d)通过X 射线光子关联谱实验测量的Mg65Cu25Y10 非晶合金在不同温度下的关联函数和弛豫指数(Ruta et al.2012)

5 黏弹性变形行为与微观结构非均匀性的关联性

传统金属材料的滞弹性变形主要由应力诱导点缺陷重排引起, 由线缺陷与位错承载. 非晶合金不具备这类静态结构缺陷, 其变形载体涉及数目不定的原子团簇的协同剪切转变 (Argon

1979). 合理、自洽地揭示非晶合金形变机理是本领域一个重要的前沿研究方向. 蠕变(creep)和应力松弛(stress relaxation)手段均是帮助理解并克服这一难题的有效手段, 通过观测宽温度区间内应力/应变的时空演化规律可探寻非晶合金变形过程中滞弹性或黏弹性的演变, 揭示微观尺度上的不均匀动力学行为. 依托这些手段可将微观结构非均匀性与动力学非均匀性联系起来, 为非晶合金在工程应用中提供基本的变形机理.

5.1 结构非均匀性与动力学非均匀性

非晶合金在宏观上表现出各向同性, 但在纳米尺度上呈现结构非均匀性. Ichitsubo 等(2005)通过超声振动与温度相结合的方式使Pd 基非晶合金中部分区域优先晶化, 进而在高分辨透射电镜下可清晰识别原子强度、密度和激活能较低的软区, 如图20(a)所示, 非晶合金的软硬区思想也侧面佐证了微观结构非均匀性. 微观结构非均匀性在形变时表现出动态非均匀性, 如应力松弛并非呈现单一弛豫模式, 而是多个弛豫过程叠加 (Qiao et al. 2019b). 图20(b)为La60Ni15Al25非晶合金在不同温度下的应力松弛曲线, 采用KWW 方程拟合可得到不同温度下的动力学演化.图20(c)为βKWW随温度的演化过程. 较低温度下非晶合金内能量较高的流变单元参与运动, 此时非均匀程度较高; 温度升高至β 弛豫温度, 软区之间发生协同运动,βKWW趋于稳定. 玻璃转变温度处大量原子运动被激活, 大量软区贯通并发生流动, 应力松弛时间尺度接近体系弛豫时间(通常为103s),βKWW趋近于1, 在动力学上接近均一化 (Wang et al. 2014). 然而非晶合金微观尺度上的弛豫特征并非完全一致, Ruta 等(2012)采用X 射线光谱分析非晶合金原子尺度弛豫, 发现βKWW＞1 的异常弛豫现象, 表明弛豫过程同样与原子间作用力有关(图20(d)).

5.2 应力松弛行为的解耦

非晶合金应力松弛行为在玻璃转变温度以下呈现出双阶段现象, 即弛豫劈裂行为. 图21 为Zr 基非晶合金不同温度下的应力松弛曲线, 近玻璃转变温度时应力随时间呈现平滑衰减, 温度降低时弛豫曲线解耦为快弛豫和慢弛豫 (Luo et al. 2017). 双阶段弛豫速率皆呈现温度相关性, 快弛豫对应于原子尺度内应力驱动的类弹道运动, 慢弛豫主要源于更大尺度的原子重排, 与微观结构非均匀性相关. 非晶合金在温度窗口内表现出不同的弛豫过程, 弛豫机制在玻璃转变温度以上为类似颗粒在笼子内的振荡(cage rattling)以及逃出笼子的过程. 温度降低时弛豫速率减缓, 呈现为对应大范围原子重排运动的α 弛豫及对应局域原子重排运动的β 弛豫. 当温度进一步降低时,非晶合金表现出由局部内应力释放引起的类弹道运动, 即快动力学模式(faster mode), 将与非晶合金本身弛豫(slower mode)发生解耦现象 (Luo et al. 2017).

图 21 (a)Zr44Ti11Cu10Ni10Be25 非晶的应力弛豫曲线,(b)弛豫速率及(c)指数随温度的演化,(d)非晶合金及其高温前驱液体的动力学行为的Arrhenius 图(Luo et al.2017)

图 22 (a)Cu46Zr46Al8 非晶合金在低温弛豫时的双阶段现象(Qiao et al.2016b);(b)应力驱动到热激活应力松弛的转变.插图显示例如在403 K,表明松弛机制随应力变化的明显转变(Qiao et al.2016b);(c)Pd40Ni40P20 非晶合金在X 射线光子关联谱下的弛豫时间随温度的演化(Zhou et al.2020);(d)聚合物的焓弛豫时间随温度变化(Cangialosi et al.2013)

同样地, 其他典型体系非晶合金应力松弛过程也表现出明显的双阶段现象, 图22(a)(b)中非晶合金应力松弛曲线在低温时同样呈现双阶段现象 (Qiao et al. 2016a). 这两个过程分别对应热激活引起的慢过程和应力激活的快过程, 双阶段的弛豫激活能介于其β 弛豫及α 弛豫之间表明双阶段的现象并非由常见弛豫模式直接引起 (陈迎红等2020). 慢弛豫过程中表现出更小的激活体积, 激活能能垒主要由热驱动克服而非应力主导 (Luo et al. 2017). 快过程对应的激活体积较大, 松弛过程中快过程是由应力驱动主导的原子移动. 温度接近玻璃转变温度时弛豫过程中也会出现形变激活能的转变, Zhou 等(2020)在对高压扭转处理后的Pd40Ni40P20非晶合金原子结构的弛豫特征研究中发现, 低温下弛豫过程受应力主导, 高温下弛豫过程由应力主导转变为扩散主导, 伴随着激活能的增加 (图22(c)). 此外, Cangialosi 等(2013)在焓弛豫实验中发现聚合物玻璃趋向于平衡态的过程同样分化为两个阶段(图22(d)), 进一步证实弛豫机制的复杂性及其动力学非均匀性特征. 两步弛豫过程中, 较快的弛豫过程与反常应力主导的微观动力学有关, 较慢的弛豫过程与更大尺度的扩散运动有关, 这表明微观原子运动与宏观弛豫行为存在直接联系. 弛豫动力学在深冷玻璃态的解耦导致的两步应力松弛现象扩展了人们对玻璃态的认识, 突破了对弛豫的传统理解, 为理解非晶合金的黏弹性行为提供了新的思路.

5.3 蠕变行为

深入研究非晶合金的蠕变行为对解释其结构弛豫行为、变形机制和力学性能等具有重要指导意义, 蠕变过程中非晶合金的总变形包括瞬时弹性变形ϵe,可恢复的黏弹性变形ϵa以及不可恢复的黏塑性变形ϵV. 目前普遍应用如图23(a)所示的广义Kelvin 模型来描述蠕变行为, 应力应变响应可表示为:,Ei为第i个弹簧单元的弹性模量,为第i个黏壶单元的弛豫时间 (Cost, 1983). 此模型兼顾非晶合金微观结构非均匀性及动力学非均匀性, 可以构建不同应力及温度下非晶合金蠕变过程中的弛豫时间分布图谱 (Xu et al. 2020).如图23(b)所示, 弛豫时间谱可以清晰直观地表征不同变形单元弛豫时间强度的应力及温度相关性. 在低温、低应力条件下, 弛豫时间分布单一且对应强度较低; 而在高温、高应力条件下, 弛豫时间分布发生展宽且强度增强.

图 23 (a)由n 个Kelvin 单元和1 个Maxwell 单元组成的广义Kelvin 模型,(b)不同应力及温度下La56.16Ce14.04Ni19.8Al10 非晶合金蠕变过程的弛豫时间分布图谱(Xu et al.2020)

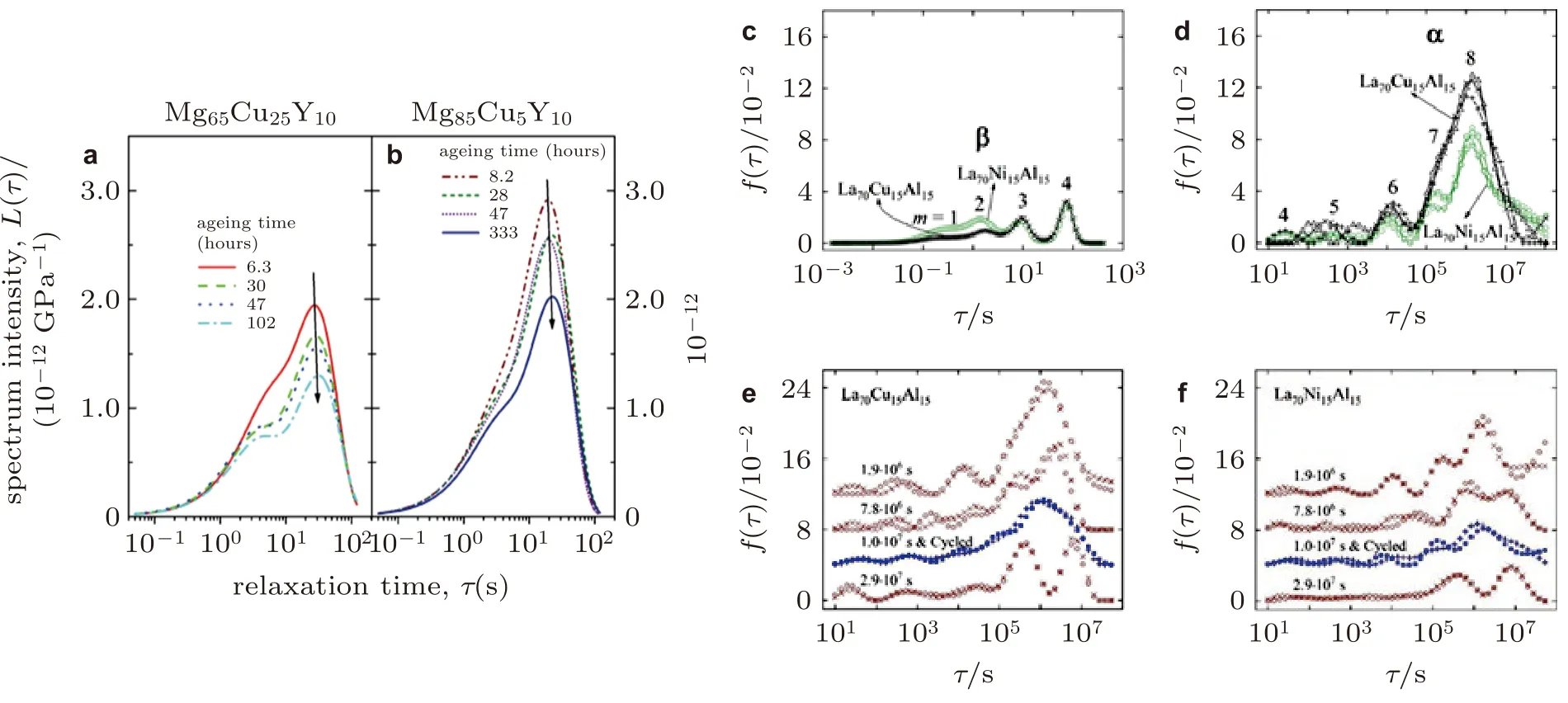
图 24 (a)Mg65Cu25Y10 和(b)Mg85Cu5Y10 非晶合金的弛豫时间谱(Castellero et al.2008),(c)La70Cu15Al15和(d)La70Ni15Al15非晶合金物理时效后的弛豫时间谱(Lei et al.2020),(e)La70Cu15Al15和(f)La70Ni15Al15 在物理时效和低温循环下非晶合金的弛豫时间谱(Lei et al.2019a)

随着对非晶合金蠕变行为的深入研究, 人们相继发现了非晶合金呈现明显的分阶段蠕变现象, 对应于不同的蠕变机制 (Zhang et al. 2021a). 晶体合金与非晶合金在纳米压痕实验中发生了相似的软化现象, 晶体内的位错和非晶合金内的STZ 这类变形单元的应力驱动-温度辅助(stressdriven temperature-assisted)激活动力学均遵循普遍的焓-熵补偿准则 (Wang et al. 2013, 2015b).这种塑性软化背后的物理机制均起源于晶体内位错或非晶内STZ 的相似协同运作模式 (Zhang et al. 2019). Krisponeit 等(2014)发现了明显的阶梯蠕变行为, 阶梯间等待时间频次与交叉时间之间遵循不同的幂律分布. 进一步地, 这种幂律转变被归因为STZ 在三维尺度的随机激活向二维尺度内纳米剪切带的转变 (Herrero-Gomez and Samwer 2016). 本课题组分析了La 基非晶合金蠕变柔量对应力及温度的相关性, 发现非牛顿变形特征与微剪切畴在应力或温度激励下依次发生的生成、扩展以及不可逆的融合过程有关 (Qiao et al. 2019a). Cao 等(2017)模拟典型Cu50Zr50非晶合金在实验时间尺度上的蠕变过程, 证实非晶合金的变形在低应力下由扩散主导,而在高应力下是由应力诱导的局部剪切变形.

非晶合金的黏弹性行为起源于其内部原子松散排列区域的局域重排, 由于这类松散区域具有不同模量、激活能和弛豫时间等物理特征, 这一过程是动力学非均匀的. 通过引入n个变形单元(缺陷)的弛豫时间τi, 学者们提出用弛豫时间谱(relaxation-time spectrum)解释非晶合金变形过程中的动力学非均匀性, 尝试将宏观变形行为与其微观结构关联起来. 如图24(a)(b)所示, Cu元素原子的增加会赋予非晶合金更致密的微观结构, 退火过程通过诱导缺陷湮灭使其致密程度加剧, 但仅对尺寸较大、弛豫时间较长的缺陷有影响, 而对尺寸较小、弛豫时间较短的缺陷影响微乎其微 (Castellero et al. 2008). 在热力耦合作用下, 非晶合金内部原子团簇通过一系列剪切转变过程来适应局部变形 (Argon 1979). 作为微观变形载体, STZ 在体积大小、数目及激活能等方面存在较大差异. 一个直观证据来自于STZ 作用时间, 在高应变速率纳米压痕实验中, STZ 作用时间不长于0.01 s (Ye et al. 2010), 而在准静态弯曲实验中, 其作用时间长达107s (Ju et al. 2011).此外, STZ 作用强度也存在较大差异, 如图24(c)(d)所示, STZ 的弛豫时间分布跨越了11 个数量级, 且峰强、峰宽的分布各不相同. 对于较短的弛豫时间(0.01 ~ 5 s), 其内部机制对应于非晶体系的β弛豫行为; 而更长的弛豫时间(＞5 s)则与α弛豫行为紧密相关(Lei et al. 2020, 2019a, 2019b).具有显著β 弛豫的La70Ni15Al15非晶合金在较短实验窗口内具有更大的黏弹性变形和更快的STZ 激活过程, 而在长时间窗口内呈相反趋势, 这与La70Ni15Al15非晶合金更小尺寸、更快激活速率的STZ 单元有关 (Lei et al. 2020). 从能量状态出发, 物理时效和低温循环对STZ 激活过程的影响如图24(e)(f)所示. 物理时效促驱使弛豫时间谱峰强降低、整体弛豫时间逐渐升高以及STZ 体积分数下降. 低温循环过程类似于年轻化(rejuvenation)处理, 部分逆转了这一趋势. 上述分析方法引入连续分布的弛豫时间, 可反映不同时间尺度事件的分布从而精确描述非晶合金的动力学非均匀性, 已成为探索黏弹性变形机制的主要方法 .

6 力学激励调控非晶合金微观结构非均匀性

非晶合金在构型空间上仅占据自由能局域的极小点, 在热力学上具有自发地向能量更低的平衡态演化的趋势, 伴随着结构和性能的演变, 年轻化处理对应于非晶合金势能图谱的一种多层级自组装过程, 能够有效提高非晶合金的能量状态, 引入更多自由体积, 使非晶合金“返老还童”(Bouchaud et al. 2001, Peter 2009). 通常采用弛豫焓定量表征年轻化程度(如图25(a)热流曲线的面积). 非晶合金年轻化通常可通过是否发生形变分为形变法(弹性加载,非均匀塑性形变的冷轧、快速冲击、高压扭转、热力蠕变等)和非形变法(冷热循环、辐照、磁性加载等), 不同的制备或处理方式可引引入不同的能量状态, 如图25(b)中所示. 从热力学角度出发, 非晶合金的“年轻化”可看做是结构向能量更高、熵更大的无序状态转变的过程 (Pan et al.2018, Tong et al. 2015), 如图25(c)所示. 值得注意的是, 非晶合金的年轻化处理不仅是物理老化的逆过程. 物理老化是非晶合金长时间结构弛豫的自发结果, 而年轻化处理需要在外部的激励下实现.

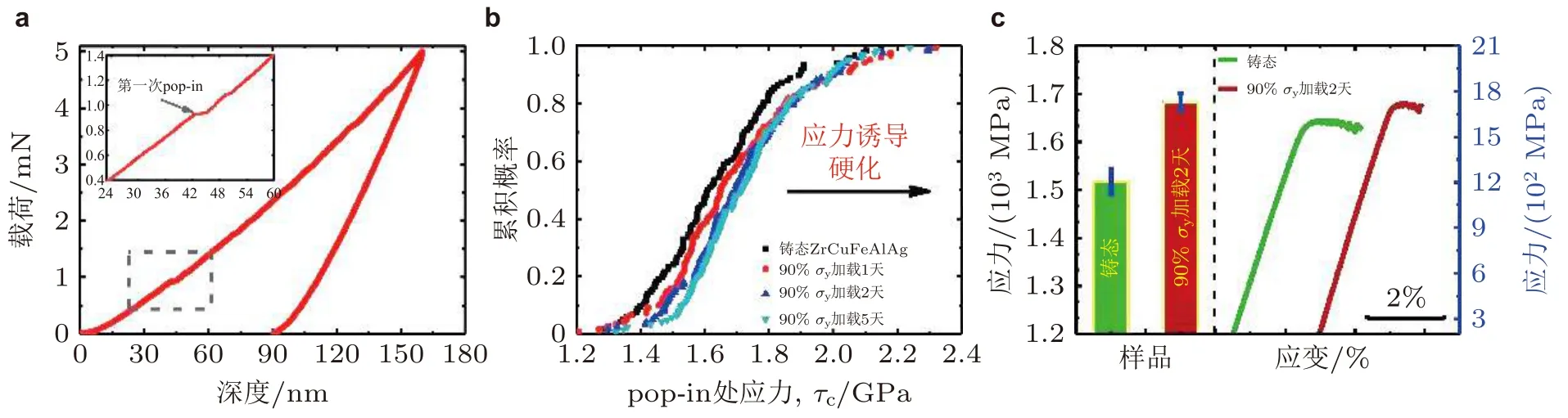
图 26 (a)铸态Zr 基非晶合金荷载−深度曲线,(b)铸态及预加载不同时长的非晶合金试样临界剪切应力的累积概率分布,(c)弹性静力压缩2 天前后的屈服应力和应力−应变曲线(Wang et al.2015c)

6.1 弹性加载

在弹性加载的过程中非晶合金内部局域结构从周围吸收热量, 发生改变 (Greer & Sun 2016).局域弹性模量波动在弹性循环加载后显著增大, 表明非晶合金年轻化行为与纳米尺度弹性波动有关, 大量局部区域软化导致整体结构软化 (Ross et al. 2017). 弹性静态压缩后非晶合金发生塑性变形, 弛豫焓降低, 密度、临界剪切应力和屈服强度增大, 如图26 所示, 弹性静态压缩使非晶合金表现出显著的结构弛豫(应力诱导自由体积的湮灭)和致密化现象 (Wang et al. 2015c). 非晶合金结构能够在低于屈服强度的应力水平下发生变化, 其变化速率取决于初始原子堆积密度. 弹性加载对非晶合金力学性能的影响与合金组分、初始状态以及加载方式有关 (Priezjev 2019).

6.2 冷轧

高度塑性变形(冷轧、高压扭转等)可以改变非晶合金的能量状态, 这些方式通常被认为可以增加自由体积含量 (Ebner et al. 2018, Song et al. 2011). 塑性流动过程中剪切带附近的体积被局部加热至Tg甚至更高, 变形完成后立即淬火至室温, 这可能是引起结构年轻化并提高塑性的原因 (Bei et al. 2006, Dmowski et al. 2010, Lewandowski & Greer 2006). 通常提示变形能力的方法是通过增加剪切带形成的能力来增加剪切带的数量和/或通过阻止激活的剪切带的传播来实现的. 本课题组借助动态力学分析和纳米压痕的手段对比分析了多种结构状态下结构非均匀性的演化规律, 发现冷轧可较大程度上改善非晶合金结构非均匀性 (Tao et al. 2021), 如图27 所示. 统计分析pop-in 事件可获得pop-in 累计分布函数, 进而定量估算STZ 尺寸. 对比弛豫态和年轻化态, pop-in 荷载呈现出降低趋势. 冷轧可降低STZ 尺寸和激活能, 塑性变形通过激发更多的STZ成核位点引起年轻化现象, 换言之, 冷轧过程中结构非均匀性增强从而改善了塑性变形.

6.3 高速冲击

Ding 等(2019)通过基于轻气炮装置的双靶板平板撞击技术, 实现了典型Zr 基非晶合金在约365 ns 内快速年轻化到一种高焓极端无序状态. 对非晶合金施加几个吉帕量级的单脉冲加载和瞬态自动卸载, 从而避免剪切带、层裂等材料动态失效; 同时通过控制飞片撞击速度可使非晶合金的快速年轻化“冻结”在不同水平. 从热力学、多尺度结构和声子动力学玻色峰三个角度, 对非晶合金的超快年轻化过程进行了全面研究, 揭示出非晶结构年轻化源于纳米尺度团簇以“剪切转变”模式诱导的自由体积产生. 基于这一物理机制定义了无量纲Deborah 数, 解释了非晶合金超快年轻化的时间尺度可能性. 同时基于玻色峰角度, 发现非晶合金中年轻化程度与其低温比热的玻色峰强度呈正相关性(如图28), 意味着非晶合金的年轻化现象不仅与原子尺度自由体积的增加有关, 也可能与非晶内中、长程尺度的结构运动相关. 该工作使非晶合金结构年轻化的时间尺度提高了至少10 个数量级, 拓展了这类材料的应用领域, 也加深了人们对非晶合金超快动力学的认知.

图 27 (a)代表性荷载位移曲线,(b)不同结构状态下pop-in 事件累计分布函数,(c)ln [ln(1-f)-1]与不同结构状态(铸态,冷轧程度为 80% 和 90%,退火态)τmax分布的线性拟合(Tao et al.2021)

结构年轻化是深入理解非晶合金无序结构和动力学的一条行之有效的途径. 结构年轻化需要借助外部能量, 其速率快慢、等级水平和空间分布取决于外加载荷的幅值、时间和应力状态等条件 (蒋敏强和高洋 2021). 非晶合金的结构年轻化的物理机制不仅仅表现为原子尺度自由体积的产生或热焓的提高, 而且涉及中程, 甚至长程空间尺度的结构运动. 依赖于内外因素, 贡献非晶合金结构年轻化的动力学弛豫事件可以发生在不同的时空尺度. 可以用能量势垒理论(energy landscape theory) 来描述非晶合金的物理老化及结构年轻化这些过程. 一定温度下, 能量鞍点对应于不同山脉的山峰(能量势垒), 而能量谷点对应于山谷(能量局部极小态). 在外加力学激励下,非晶合金在这些山峰与山谷之间跃迁, 图29 就形象地表达了这个转变过程. 即便是在室温下, 非晶合金仍会自发地发生老化行为, 因此实现结构年轻化的过程是老化与年轻化的动态竞争. 当输入的能量高至足以使非晶合金翻越较大的能垒, 即从山谷流动至山峰时, 非晶合金对外表现为结构年轻化.

图 29 结构年轻化和弛豫的能量地形关系图(Tao et al.2021)

7 总结与展望

“结构决定性质, 性质决定用途”是广泛为人所接受的自然规律, 非晶合金由于其独特的无序结构而具有众多优异的力学和物理性能. 本文较为系统地介绍了目前基于微观结构非均匀性的非晶合金力学行为的研究工作, 尤其着重于非晶合金的宏观力学行为与微观结构非均匀性之间的关联.

非晶合金是多组元的无序原子所堆积出来的凝聚态物质, 其在空间结构及动力学行为方面是十分复杂的. 宏观上非晶合金虽然表现为均匀且各向同性, 但在微观上具有纳米到微米级别的结构与动力学非均匀性. 非晶合金的结构弛豫、扩散、断裂、流变等行为与结构非均匀性之间存在密切关联, 通过调控非晶合金的结构非均匀性为改善非晶合金的力学响应特性提供了可能性.

自20 世纪50 年代以来, 非晶合金的原子结构由简单的无规密堆结构逐渐演化到目前具有代表性的原子团簇网络. 原子结构的研究手段也从低效的球棍模型逐步发展到计算机模拟, 为理解非晶合金复杂的三维原子构型提供了极大帮助. 非晶合金的研究离不开实验表征技术与计算机模拟技术的迅速发展, 但也应注意到当前研究的局限性. 迄今为止, 已经有超过上千种非晶合金体系被开发并研究, 但是对于化学组成成分对非晶合金的形成能力及相关物理特性之间的影响仍未有统一认识. 受限于实验表征技术, 大多数实验研究仅停留在对非晶合金宏观尺寸及临界冷却速率上的表征, 而缺乏对合金液体在冷却过程中不同原子的重排运动的直观图像. 同样地, 计算机模拟使人们对非晶合金原子级别结构的团簇拓扑结构的研究得到了深入发展, 然而面对非晶合金复杂的无序原子结构, 计算机模拟也表现出一定的不足: 原子之间相互作用与真实相互作用之间存在差异, 而且受限于计算能力, 通常模拟体系的空间、时间尺度也远远小于真实尺度.因此如何跨越时间和空间障碍是当下非晶合金计算机模拟所面临的一大难题. 当前的原子团簇模型对于理解非晶合金的相关物性方面存在一定的困难, 因此探索新的非晶原子结构也是当下研究的紧要任务. 当前对于结构的描述主要集中在短程序以及中程序, 这些参量并不能完美地描述非晶合金非均匀性的结构特征, 因此能否寻找到统一的结构参量来描述非晶合金微观非均匀性与材料物理特性之间的关联也是未来研究需要考虑的重点.

非晶合金的研究仍然处于探索初期, 目前的实验研究大多是通过不断试错而不是基于完善的理论基础, 这种“炒菜式”的尝试往往费时费力, 同时很难通过人力从大量实验数据中发现材料本身所蕴含的普适规律. 值得庆幸的是, 当前基于高通量方法的实验能够做到快速研究上百甚至上千种组分连续变化的非晶合金的物理特性, 而且基于人工智能的机器学习技术, 可以从海量实验、仿真数据中提取出有效关联. 这些新的研究技术和方法将为今后非晶合金组分设计、性质调控等提供指导, 大大加快非晶合金的研究进展. 这个世界是混沌的, 人们所了解的世界远远小于未知的世界, 这种无序性体现在太多的自然现象无法得到解释和预测. 从小到原子尺度至大到宇宙尺度, 无序和不均匀都是共同的话题. 正是充满了无序和混沌, 世界才会显得多姿多彩, 也正是不均匀的存在使得宇宙有能量的流动, 才有了孕育出生命的可能性. 即便如此, 在无序未知的世界里抓住“有序”的规律并非易事, 需要时间的积累也需要一代代科研工作者为之努力付出, 也许终有一天人们能够揭开非晶合金无序结构的神秘面纱, 理解这纷杂喧闹的世界.

在这里提出几个值得去探索的问题:

(1) 普遍认为过冷液体弛豫、应力松弛、结构弛豫等过冷液体和非晶合金中所表现的宏观非指数弛豫特征源于过冷液体和非晶合金的微观结构非均匀性, 即密度或某些局部结构的空间波动, 然而微观结构非均匀性与宏观非指数弛豫特征的关联仍待建立.

(2) 非晶合金中常见的力学弛豫模式, α 弛豫、β 弛豫和快β′弛豫彼此之间, 及其与非晶合金固有的微观结构非均匀性、原子扩散之间的关联. 玻璃转变温度以下大规模原子运动被冻结, 此时非晶合金在蠕变、应力松弛等力学变形过程中的原子运动与非均匀结构如何与β 弛豫关联在一起.

(3) 由于非晶合金非均匀的无序结构难以表征和模型化, 对其缺陷结构缺乏认识, 因而难以对其结构耗散外力、发生变形的过程进行理解和描述. 因此, 建立描述非晶合金结构特征的新概念和新方法, 以及独特结构的变形机制和物理模型也至关重要.

(4) 非晶合金兼具弹性固体和黏性流体的特征,其对外加载荷的应变响应通常可通过对时间依赖性和卸载之后的回复程度解耦为理想弹性应变、黏弹性应变、黏塑性应变和瞬时塑性应变. 非晶合金微观结构非均匀性在变形过程中表现出动力学非均匀性, 尽管扩展指数弛豫行为和离散弛豫谱图等可以较好地描述非晶合金的黏弹性变形行为, 但其力学本构和物理机制仍有待进一步完善.

(5) 即便是在远低于屈服应力的外加载荷下, 非晶合金仍会发生塑性变形, 出于非晶合金作为结构材料使用的安全性需求, 对其屈服、断裂机制, 蠕变和疲劳损伤行为仍缺乏深入认识.

(6) 非晶合金微观结构非均匀性的调控也是至关重要的, 例如结构弛豫和年轻化. 合适的调控方式以及其具体工艺参数确定也是推进非晶合金产业化应用的重点之一.

致 谢国家自然科学基金(51971178)、陕西省杰出青年科学基金(2021JC-12)和西北工业大学博士论文创新基金(CX2021015)资助项目.