基于HLNS 方法对高超声速边界层中非模态扰动演化的研究
孙培成 赵 磊 董 明
1 天津大学机械工程学院, 天津 300072
2 中国科学院力学研究所非线性力学国家重点实验室, 北京 100190
3 中国空气动力研究与发展中心, 空气动力学国家重点实验室, 四川绵阳 621000
1 引 言
长期以来, 流动从层流到湍流的转捩一直是航空航天飞行器设计中的基础难题. 由于层流区的摩阻和热流明显低于湍流区, 准确预测转捩位置是飞行器气动力与气动热设计的关键. 当环境扰动强度较低时, 转捩过程包括模态扰动的感受性、线性失稳、非线性breakdown 和湍流四个阶段 (该过程也被称为自然转捩) . 而当环境扰动强度较高时, 转捩可能发生在模态扰动失稳区的上游, 这被称为旁路转捩或亚临界转捩. 在这一过程中, 边界层中会出现大尺度的条带结构 (也被称为非模态扰动) . 本质上, 非模态扰动是边界层系统对外界激励的响应; 即使边界层中的所有线性模态扰动都是指数衰减的, 由于它们是非正交的, 它们仍然可以合成为有限区域内代数增长的扰动 (Trefethen et al. 1993, Henningson 1995) . 在瞬态增长后, 条带结构会达到非线性饱和. 由于尺度较大, 条带本身并不会直接触发转捩, 但它会支持二次失稳扰动迅速增长, 并最终导致湍斑的出现及条带的breakdown (Zhang et al. 2018) .
有两种方法可以描述条带的瞬态增长. 第一种方法是采用边界区方程计算 (Leib et al. 1999,Ricco et al. 2011), 该方法基于渐近分析, 描述自由流中的涡扰动从平板前缘进入边界层并激发条带的过程. 另一种方法是采用最优扰动描述条带 (Luchini 2000, Tumin & Reshotko 2001, Paredes et al. 2016). 该方法不考虑外界扰动与条带之间的关联, 只通过伴随向量寻找边界层中在有限区域内增长最快的扰动. 虽然第二种方法所描述的物理过程不如第一种方法清晰, 但在较复杂 (如考虑前缘钝度和激波影响) 的超声速边界层中, 该方法的求解难度大大低于第一种方法.
壁面上的局部突变对转捩的影响是多方面的. 首先, 对于自然转捩问题, 壁面突变可以通过局部感受性 (Dong et al. 2020, Liu et al. 2020) 和线性模态的局部散射 (Wu & Dong 2016, Zhao et al. 2019, Zhao & Dong 2020, Dong & Zhao 2021, 李斯特和董明 2021) 两种机制影响转捩. 董明(2020) 曾对这两种机制进行了系统的综述. 其次, 在亚临界转捩过程中, 壁面突变可以影响条带以及二次失稳扰动的发展. 李强等 (2020) 的风洞实验表明, 凹槽可导致转捩位置提前, 且随着凹槽深度和宽度的增加, 对转捩的促进作用增强. 针对大钝度绕流问题, Paredes 等 (2017)曾建立基于线性抛物化稳定性方程 (PSE) 的最优增长理论, 研究了马赫数为7.32 的半球边界层中的非模态扰动的增长, 并考察了激波、非平行性、钝体曲率等因素对条带瞬态增长的影响. 由于PSE对原始Navier-Stokes (N-S) 方程进行了抛物化, 因而只能描述壁面缓变的情况; 而对于包含壁面突变的椭圆型问题, 该方法并不适用. 只有基于谐波型线性化N-S 方程 (HLNS) (Zhao et al. 2019)是刻画椭圆型问题的合适理论. 他们的研究表明, HLNS 方法对扰动演化的预测精度与直接数值模拟相当, 但计算量可以少两个数量级. 更重要的是, 若壁面存在由凹槽引起的流动分离, 则传统的PSE 计算发散, 而HLNS 仍然能保证良好的预测精度. 因而, 本文拟发展一套基于HLNS 方程及其伴随系统的最优扰动理论, 以揭示凹槽 (局部突变) 对亚临界转捩影响的物理机理.
2 数值方法
2.1 物理模型
本文所研究的物理模型为高超声速钝楔边界层, 如图1 所示. 选取钝楔的前缘半径R∗= 1 mm、楔角为 21.5°. 模型长度为450 mm, 取来流方向与钝楔上表面的夹角 (攻角) 为-4°. 在上表面距离前缘110 mm 的位置设置一个凹槽, 只关注上表面的边界层转捩. 坐标原点选取在上表面前缘的切点处, 选择钝头半径R∗为特征长度, 来流速度为特征速度. 因此无量纲的坐标和时间为
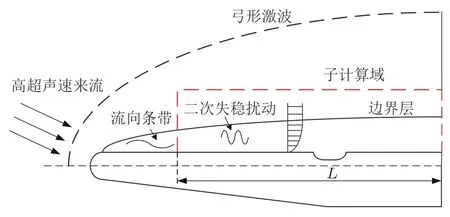
图 1 物理模型示意图
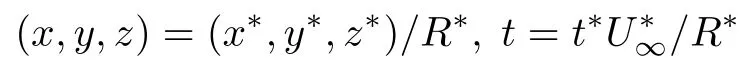
本文中, 有量纲参数加上标“*”, 来流物理量加下标“∞”. 无量纲的密度ρ、速度(u,v,w)、温度T、压力p分别定义为
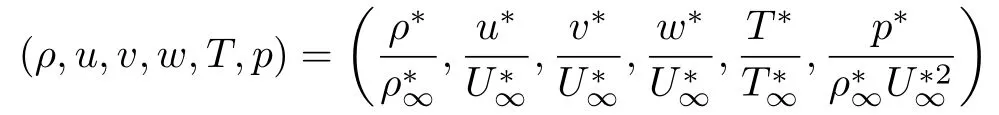
来流马赫数和雷诺数定义为
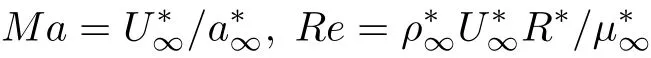
2.2 平均流与扰动场的模拟
瞬时流场q可表示为平均流和扰动场的叠加
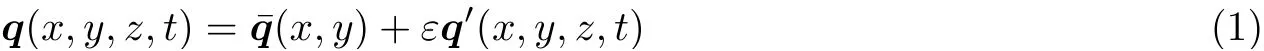
然后计算扰动演化, 用以验证本文建立的最优扰动方法的可靠性. 三维非定常直接数值模拟的方法与计算平均流的方法相同, 仍然是基于Hyps-CFD 代码, 但是要考虑展向变化与时间积分的精度. 本文的展向计算域取一个展向波长 (由扰动的展向波数确定) , 边界上选取周期条件. 计算域入口条件给定基本流与扰动的叠加, 在计算域出口采用嵌边区边界条件以消除扰动在出口边界的反射. 时间改用三阶Runge-Kutta 方法.
本文采用的数值模拟代码已被用于后掠钝平板 (Zhao et al. 2016) 、含鼓包及凹槽的平板(Zhao et al. 2019) 、含台阶及抽吸平板 (Zhao & Dong 2020) 、攻角锥 (Song et al. 2020) 等模型的稳定性与转捩研究.
2.3 基于HLNS 方程的最优扰动方法
2.3.1 HLNS 方程
在凹槽附近, 平均流的流向尺度与法向尺度相近, 因而非模态扰动的特征剖面在凹槽附近快速畸变. 这属于椭圆型问题. 在贴体坐标系(ξ,η,z)下, 扰动表示为
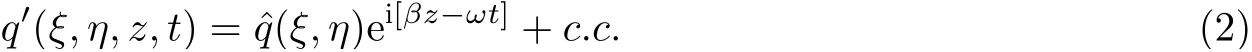
其中,ω和β为扰动的圆频率与展向波数, 它们均为实数,qˆ(ξ,η)为扰动分布函数,c.c.表示复共轭.将式(1)代入N-S 方程, 减去平均流满足的N-S 方程并略去ε2项, 可得到线性化的N-S 方程; 将式(2)代入线性化N-S 方程, 则可得到HLNS 方程
其中系数矩阵见Zhao 等 (2019). 在远场η →∞处,采用零扰动边界条件 (=0); 在壁面η=0处,采用无滑移、无穿透及等温边界条件(=0); 在计算域入口处由给定的扰动形函数(ξ0,η)作为边界条件; 出口采用出流边界条件 (Zhao et al. 2019) . 本文的HLNS 代码已被用于计算局部突变对边界层失稳模态与转捩影响的问题 (Zhao et al. 2019, Zhao & Dong 2020,Dong & Zhao 2021) .
2.3.2 最优扰动方法
为了度量扰动在给定位置处的能量, 定义两个扰动向量的内积

基于此内积空间定义能量范数

其中
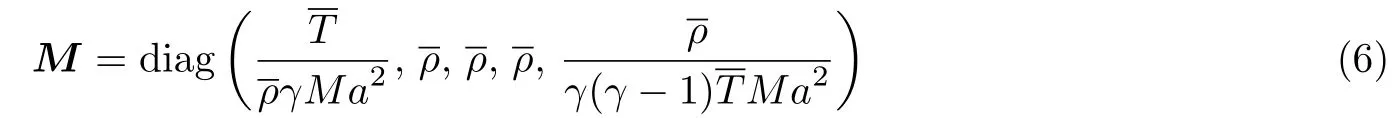
在给定区间[x0,x1]内能量增长最大的扰动被称作最优扰动. 定义目标函数为

寻找最优扰动就是求目标函数取最大值时的扰动, 此时的最优能量增益G=max[J()].
为了求解最优扰动, 采用Lagrange 乘数法建立最优系统. 定义如下内积空间

其中Ω=[x0,x1]×[0,∞]为空间计算域. 基于此内积空间, 可以定义HLNS 算子L 的伴随算子L*

其中
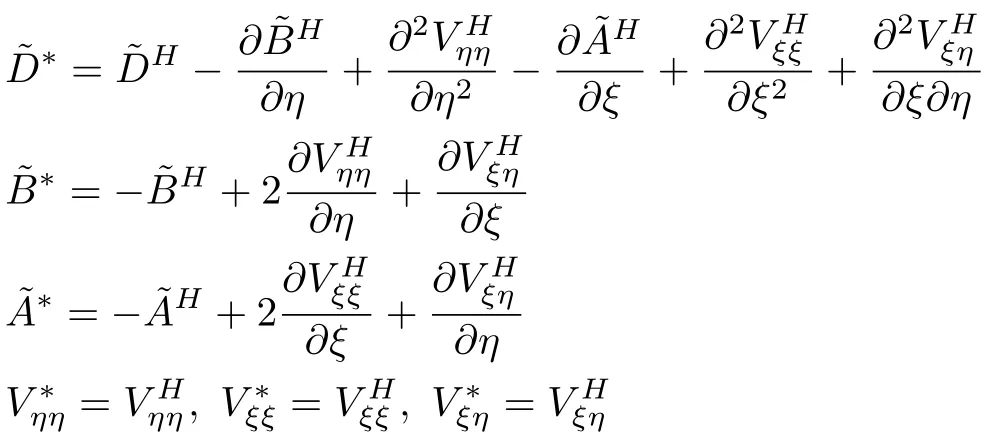
略去边界项中的高阶小量, 其最终形式表示为
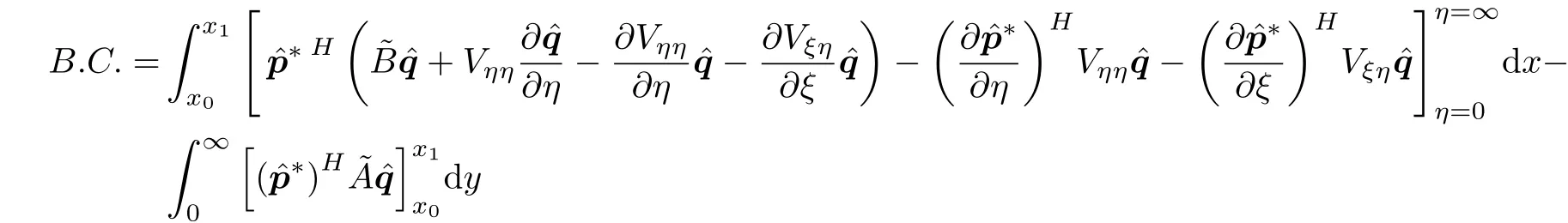
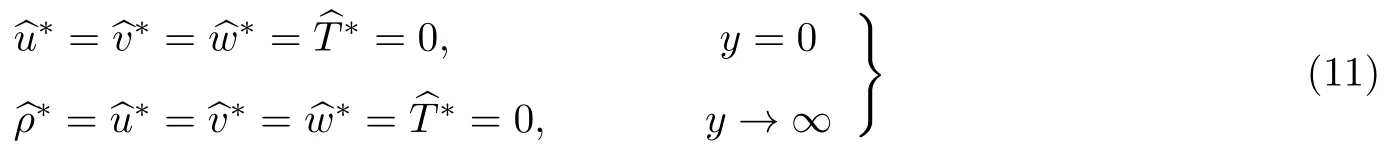
可使B.C.中的第一项为0, 得
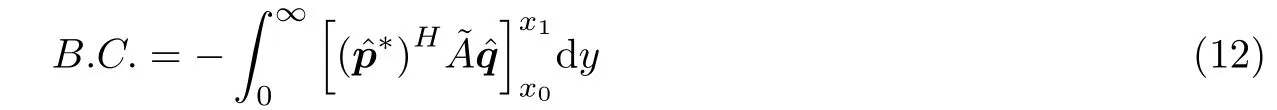
定义泛函
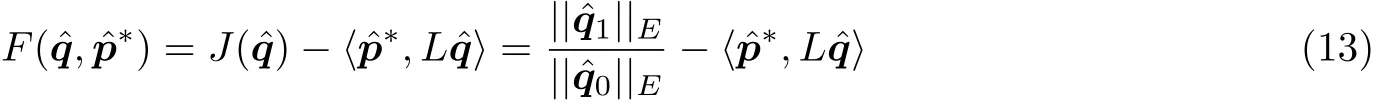
为使目标函数J()最大, 需寻求泛函的驻点, 即泛函变分

为0 的点. 这要求式(14)右边两个内积均为0. 由方程L=0可得式(14)右边的第一项为0. 将式(9) (12) (13)代入式(14)右边的第二项, 可得
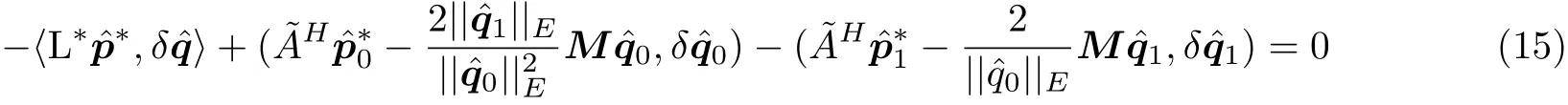
由式(15)中第一项为零, 可得

这被称作伴随HLNS 方程 (AHLNS) . 需要指出的是, 由于伴随方程与原始方程性质的差异,AHLNS 方程是以x1作为计算的入口, 以x0作为计算域的出口. 这与原始HLNS 方程正好相反. 由式(15)中第二项和第三项为0, 可得到x=x0和x=x1处的最优化条件
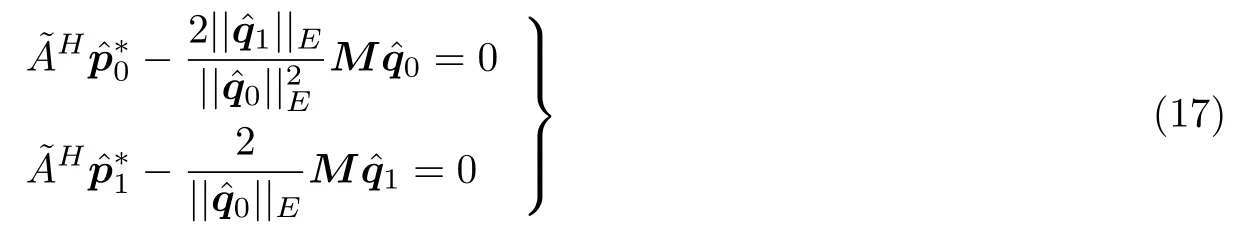
由此得到原始扰动和伴随扰动的初始条件

其中c0和c1为常数, 对于线性问题, 该常数的选取不会影响计算结果.
迭代求解HLNS 方程(3)、AHLNS 方程(16)和最优化条件(18), 可获得最优扰动及其能量增益. 迭代求解步骤如下:
(1) 在计算域入口x0处随机给定初始扰动0;
(2) 在区间[x0,x1]求解HLNS 方程;
(3) 由式(18)得到伴随扰动在x1处的初始条件;
(4) 在区间[x0,x1]求解AHLNS 方程;
(5) 由式(18)得到x0处新的扰动初始条件;
2.3.3 HLNS 与AHLNS 方程的离散
由2.3.1 与2.3.2 可知, HLNS 与AHLNS 方程在远场与壁面处采用了同样的边界条件, 在各自的计算域入口均给定扰动的分布函数, 在各自的计算域出口均采用出流边界条件. HLNS 与AHLNS 方程中的偏导数项采用5 点四阶精度的Lagrange 离散算子进行数值离散, 详细信息可参考Zhao 等 (2019) 的附录B. 对原始HLNS 方程及伴随方程的数值离散最终均产生一个代数方程组系统, 形式为

其中M为5NxNy×5NxNy维矩阵,表示5NxNy维矢量,Nx和Ny为流向及法向的网格点数,是由入口条件 () 产生的非齐次激励项. 采用因特尔数学核心库 (MKL) 求解线性系统(19).
3 计算结果及分析
3.1 计算参数及流动配置
选择激波风洞实验 (李强等2020) 的流场参数, 马赫数为5.96, 单位雷诺数Reu= 3.34 × 107m-1,来流静温= 87 K. 由于风洞实验的运行时间较短, 故壁面温度取室温= 290 K. 为了方便计算, 在凹槽的拐角处做光滑处理, 其形状分布为
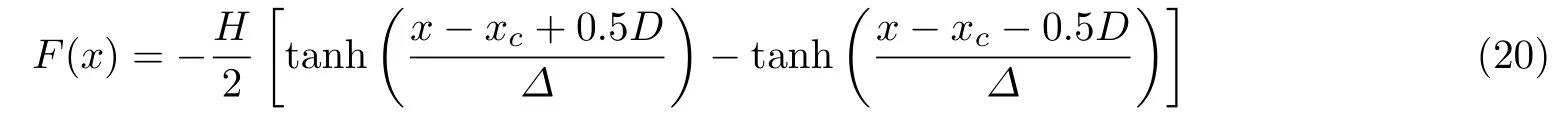
其中,H为凹槽的深度,D为凹槽的宽度,xc=110为凹槽的中心位置,Δ为定义的光滑因子, 这里取Δ=0.3968.值得说明的是, 对凹槽形状做人为光滑会降低局部散射的效应, 且Δ越大影响越大.本文的计算虽然不能完全反映实验中的工况, 但却能从原理上分析局部散射效应对条带的影响.
计算凹槽作用下的基本流时, 取流向计算域为 2 ≤ξ≤150, 法向计算域从壁面处延伸到激波外. 流向网格点共1401 个, 且在凹槽附近加密; 法向网格点共301 个, 且在壁面处较密集. 图2 展示了凹槽附近的网格系统示意图, 图中仅展示了1/2 的流向网格点与1/5 的法向网格点. 在ξ=2处将不含凹槽的光滑钝平板基本流插值到此处作为入口条件.
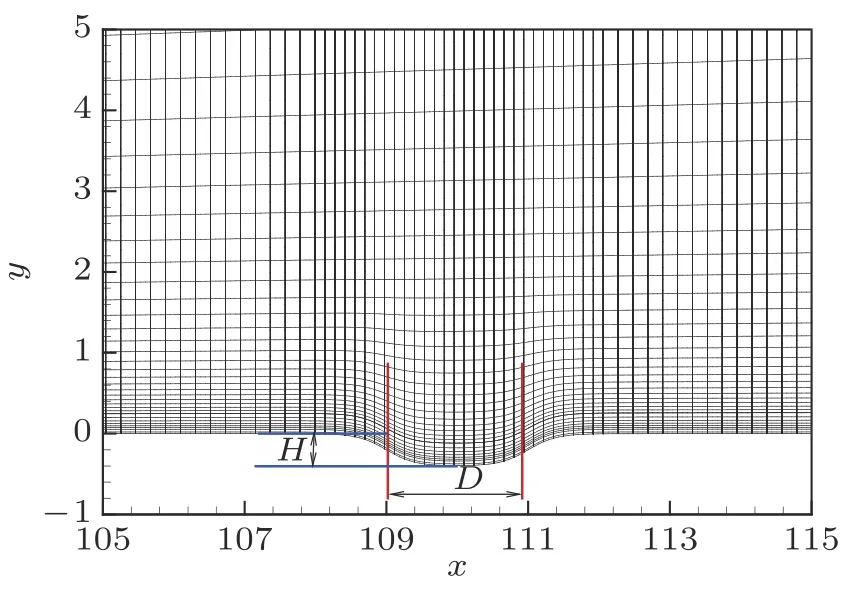
图 2 凹槽附近的网格示意图
3.2 基本流结果
固定凹槽宽度D= 2, 选择四种典型的凹槽深度 (H= 0.1、0.15、0.2、0.4) 计算基本流. 网格无关性验证见附录A. 图3 中展示了凹槽附近的平均流压力等值线云图. 凹槽对平均流压力的修正是以压缩膨胀波系的形式存在. 蓝色区域表示膨胀波, 红色区域表示压缩波. 随着深度的增大,膨胀波强度逐渐减小, 而压缩波强度先减小再增大.
图4(a)展示了不同深度凹槽下壁面速度剪切率Sw=(∂u¯/∂y)|w的流向分布,其中Sw小于0代表流动产生分离. 图中给出的四个工况均出现了分离; 随着H的增大,Sw逐渐减小, 且极小值所出现的流向位置向下游移动. 图4(b)还展示了壁面压力w沿流向的分布. 随着H的增大, 压力极小值逐渐减小, 而逆压梯度及压力峰值逐渐增大.
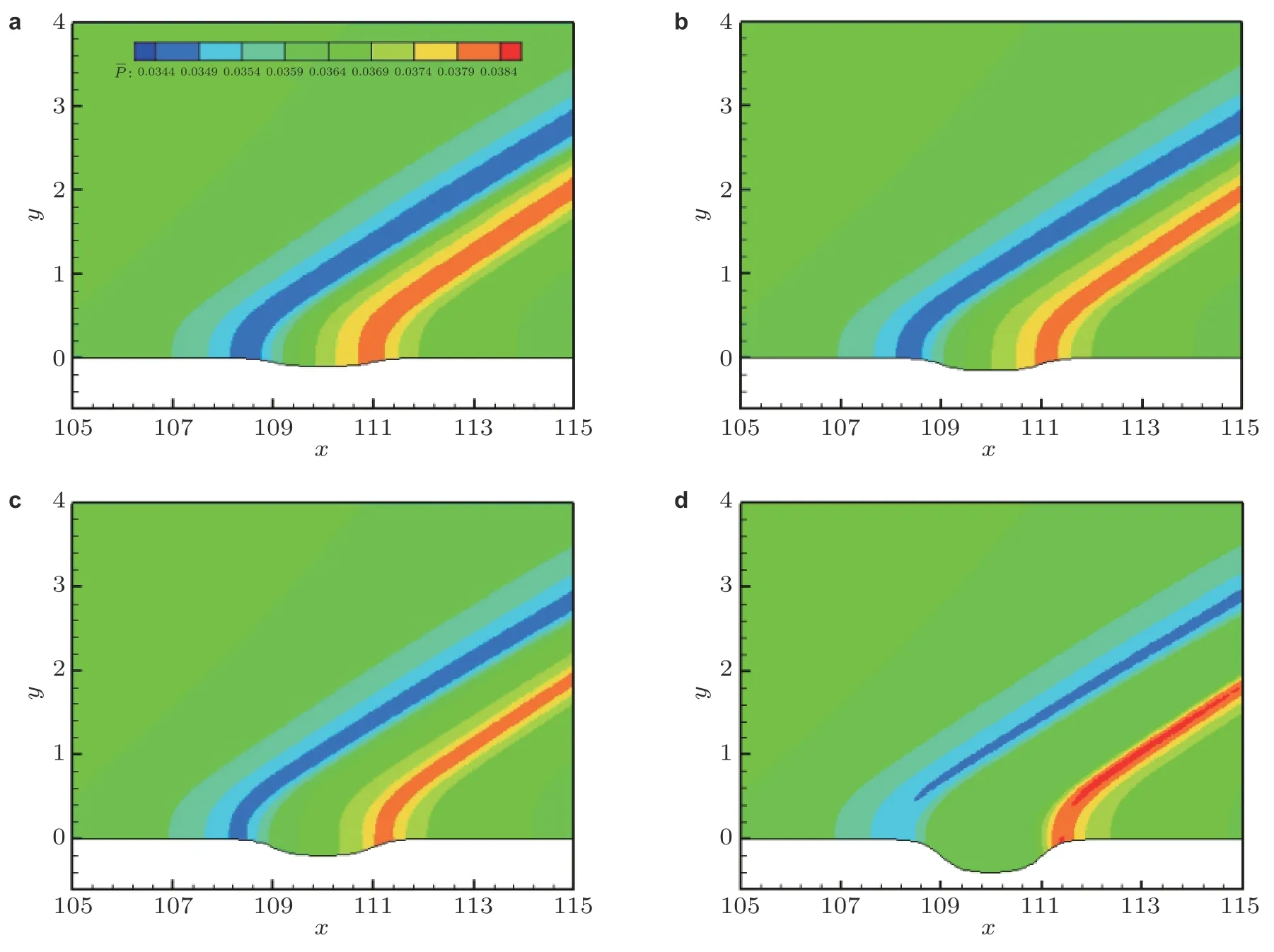
图 3 平均流压力等值线图.(a)H = 0.1,(b)H = 0.15,(c)H = 0.2,(d)H = 0.4
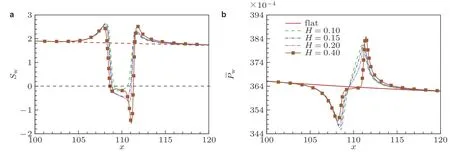
图 4 不同深度凹槽下壁面速度剪切率(a)以及壁面压力(b)的流向分布
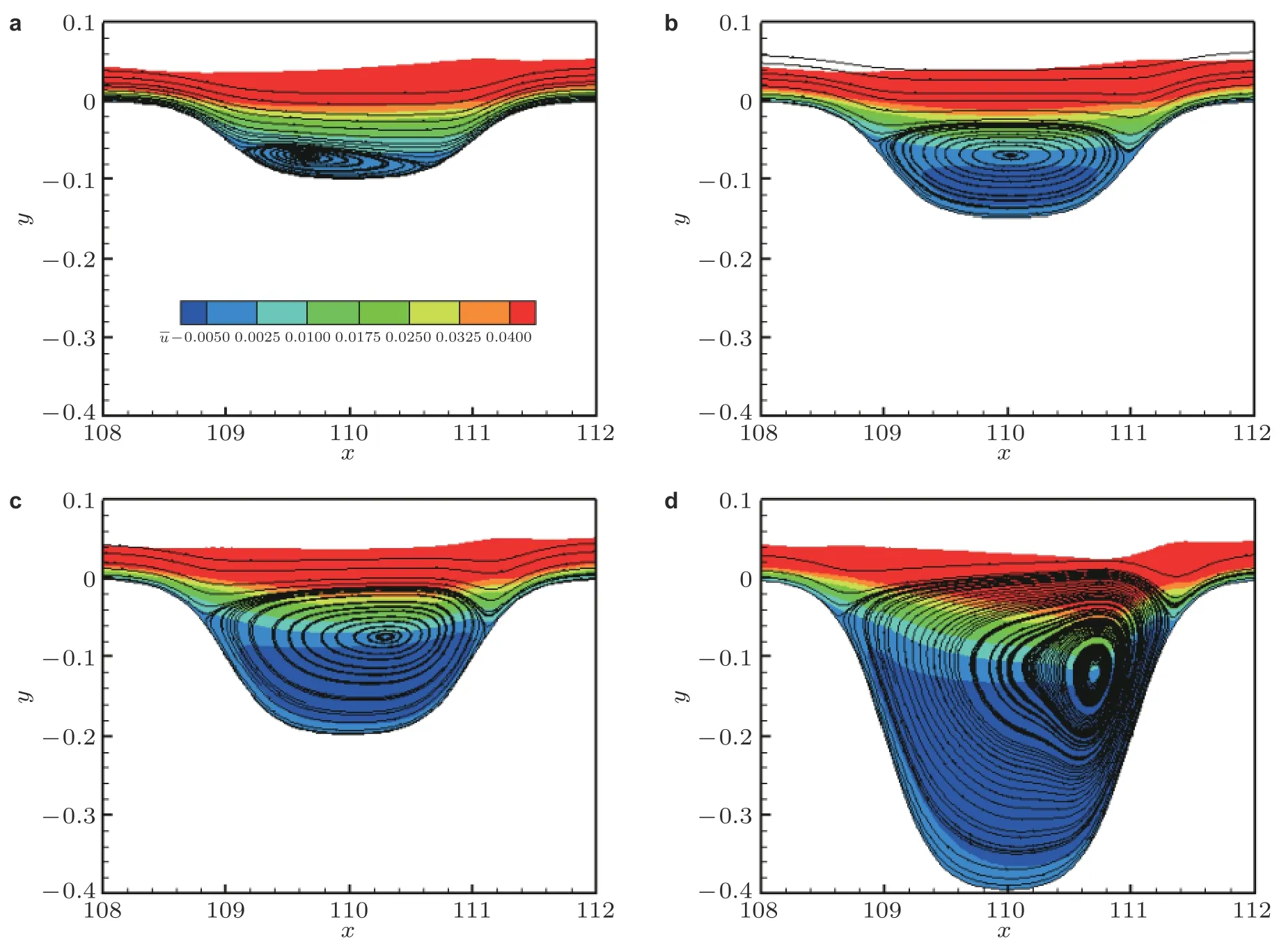
图 5 凹槽内流向速度等值线图及流线图.(a)H = 0.1,(b)H = 0.15,(c)H = 0.2,(d)H = 0.4
图5 中展示了发生分离的四种典型深度的凹槽内流向速度的等值线云图以及流线. 对于较浅的凹槽, 分离泡中心靠近凹槽左侧, 且分离泡尺寸较小; 随着凹槽深度的增大, 分离泡尺寸逐渐增大, 且分离泡的中心也向下游移动. 这一现象与矩形凹槽的情况 (Dong & Li 2021) 类似.
3.3 线性最优扰动
针对本文的物理模型及参数, 风洞实验 (李强等 2020) 测量到光滑壁面情况的转捩位置在Mack 模态线性失稳区的上游. 这说明这一转捩过程属于亚临界转捩, 早期条带的演化可用最优扰动近似描述. Tumin 和 Reshotko (2001)、Paredes 等 (2018)的研究发现, 定常条带具有最强的瞬态增长能力, 因此, 本文只研究定常条带的演化. 图6 中给出了在光滑壁面情况下, 不同区间内最优能量增益G随展向波数β的变化情况. 若计算域的入口固定, 延长计算域出口使G的峰值增加, 且最优展向波数降低 (波长增加) . 这是由于边界层随着向下游的发展而增厚, 它所对应的最优条带的展向尺度也相应增大. 若计算域的出口固定, 最优能量增益G随着入口位置的后移先增加后减小. 对于所研究的工况, 最大增益所对应的区间为[65,150], 其最优展向波数β=2.8, 此时G约为1970.
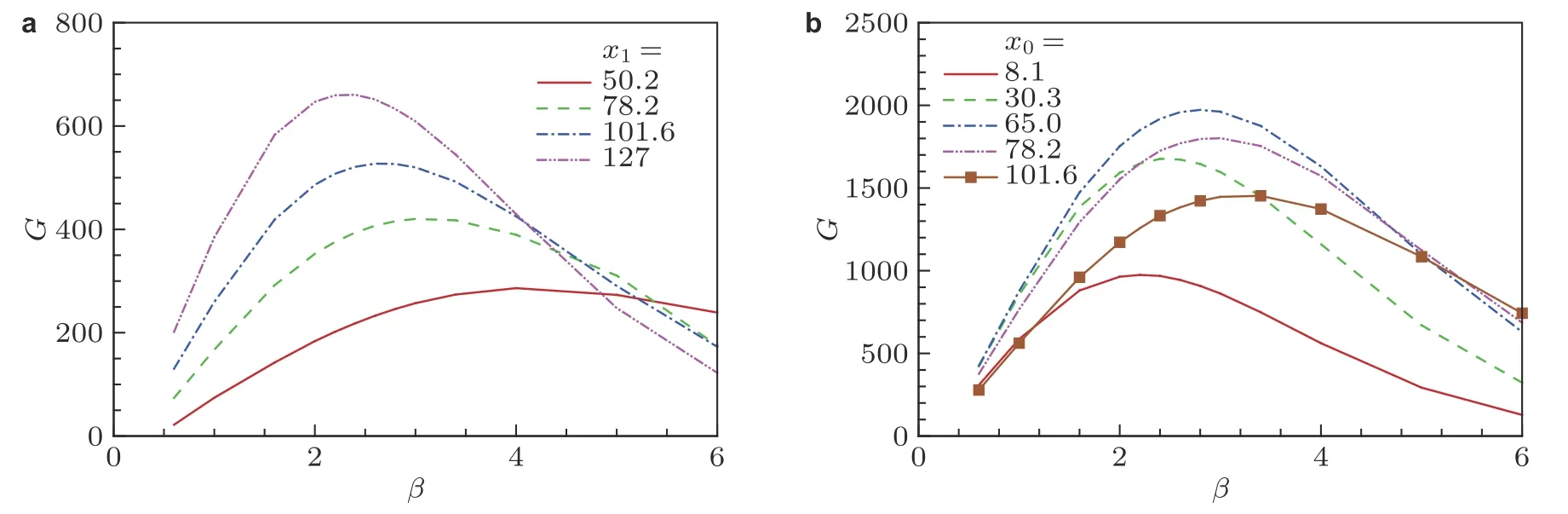
图 6 固定入口(a)、出口(b)时不同计算域下最优能量增益随展向波数的变化
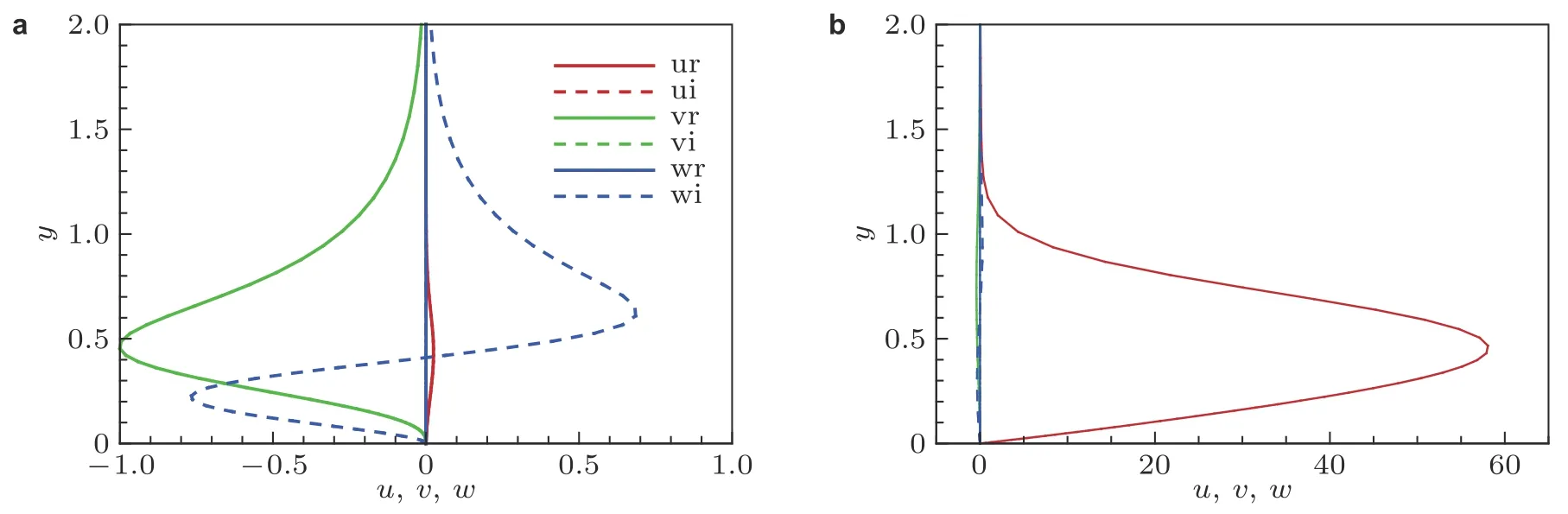
图 7 最优扰动在入口(a)、出口(b)处的特征函数剖面(β =2.8)
选择最优区间[65,150]为研究区间, 图7 给出了展向波数β=2.8的最优扰动在计算域入口、出口处的特征剖面, 其中实线为特征函数的实部, 虚线为特征函数的虚部. 图中剖面已经用入口处的法向速度脉动的最大值进行归一化. 在入口处, 流向速度扰动较小, 而展向速度扰动最大;而在出口处, 流向速度扰动在lift-up 机制下经历了显著的放大, 其幅值远大于和, 表现为如Zhang 等 (2018)模拟中的条带结构. 选择展向波数β=2.8的最优扰动, 采用DNS 方法计算扰动的演化. 由HLNS 系统预测的条带演化与DNS 结果吻合很好, 如图8(a)所示, 图8(b)展示了流向速度扰动的空间结构.
3.4 局部凹槽对最优扰动的影响
固定计算域区间为[65,150], 采用基于HLNS 及AHLNS 系统的最优扰动理论计算不同深度凹槽作用下的最优扰动能量增益. 如图9(a)所示, 各个工况所对应的最优展向波数β约为2.7 ~2.8, 局部凹槽使接近最优展向波数的最优扰动的能量增益增加, 而对远离最优展向波数的最优扰动的能量增益影响很小. 图9(b)展示了展向波数在2.6 ~ 2.9 范围内能量增益G随凹槽深度的变化, 随着深度的增大,G先增大后减小. 在深度H= 0.2 时,G达到峰值2170. 选择展向波数β=2.8的最优扰动, 采用DNS 方法计算其在H= 0.2 的凹槽作用下的演化, 由HLNS 系统预测的条带演化与DNS 结果吻合很好, 如图10(a)所示, 图10(b)还展示了凹槽影响下的流向速度扰动的空间结构.
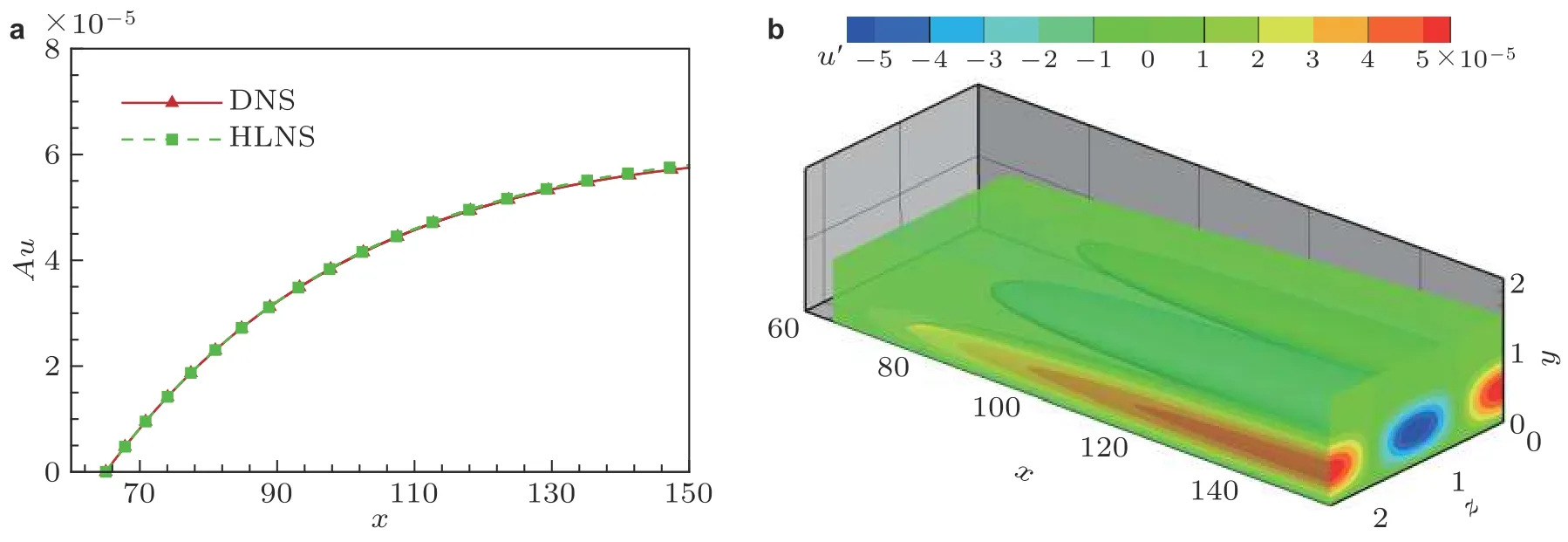
图 8 (a)HLNS 与DNS 计算的幅值Au 对比,(b)及流向速度扰动的空间结构(β =2.8)
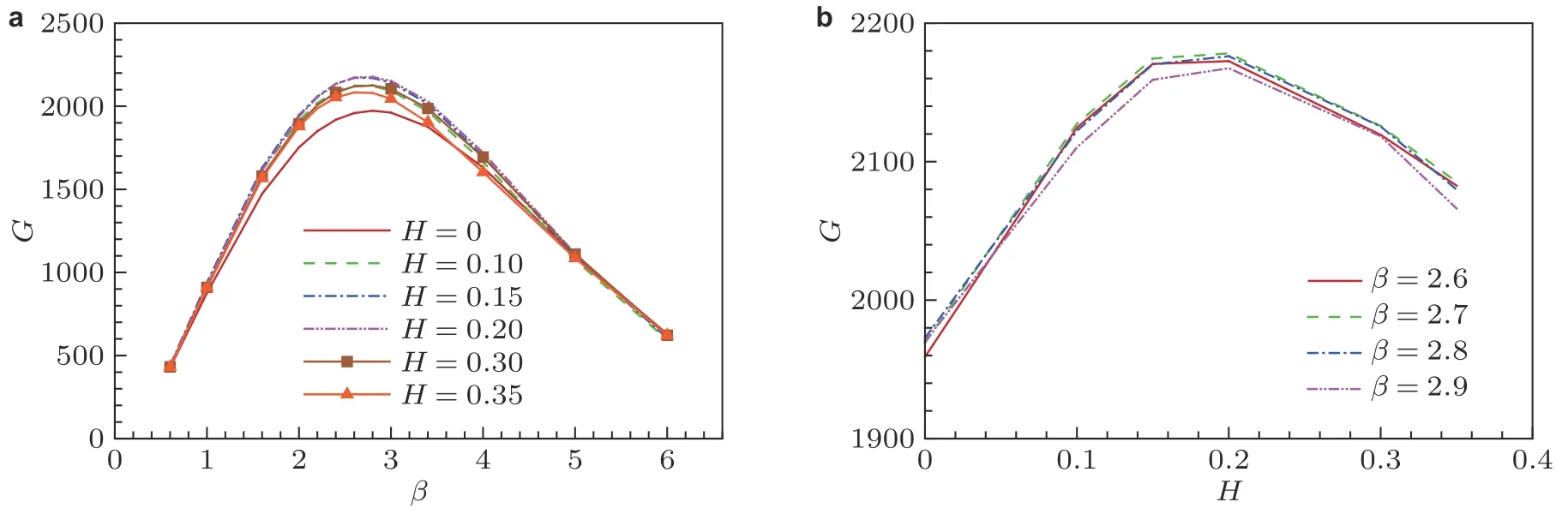
图 9 (a)不同深度凹槽下的最优能量增益随展向波数的变化,(b)最优能量增益随凹槽深度的变化
用式(5)的能量范数E(x)度 量非模态扰动的能量, 图11(a)展示了非模态扰动的能量E(x)沿流向的演化. 非模态扰动在凹槽附近发生较快速的畸变, 其能量在局部明显增加; 但随着向下游的演化, 条带在下游恢复到凹槽前的增长状态, 但幅值发生了变化. 为了度量这一变化, 引入归一化能量(x)=E(x)/E0(x),其中E0(x)为光滑壁面情况下非模态扰动的能量演化. 图11(b)展示不同深度凹槽下的归一化扰动能量. 在凹槽上游, 归一化扰动能量约为1, 表明凹槽对入口处的最优扰动及扰动在上游的演化几乎没有影响; 而在凹槽的下游, 归一化扰动能量趋于常数. 该常值可定量地刻画凹槽对非模态扰动演化的影响. 借用Wu 和 Dong (2016), Zhao 等 (2019)线性模态局部散射的概念, 定义该常数为能量放大因子T.T >1表 示凹槽促进了非模态扰动的发展,T <1表示凹槽抑制了非模态扰动的发展. 图12 展示了凹槽深度对放大因子T的影响. 不同深度的凹槽均促进非模态扰动的增长; 随着深度增大, 凹槽的促进作用先增大后减小, 且在H= 0.2 时达到峰值1.1.
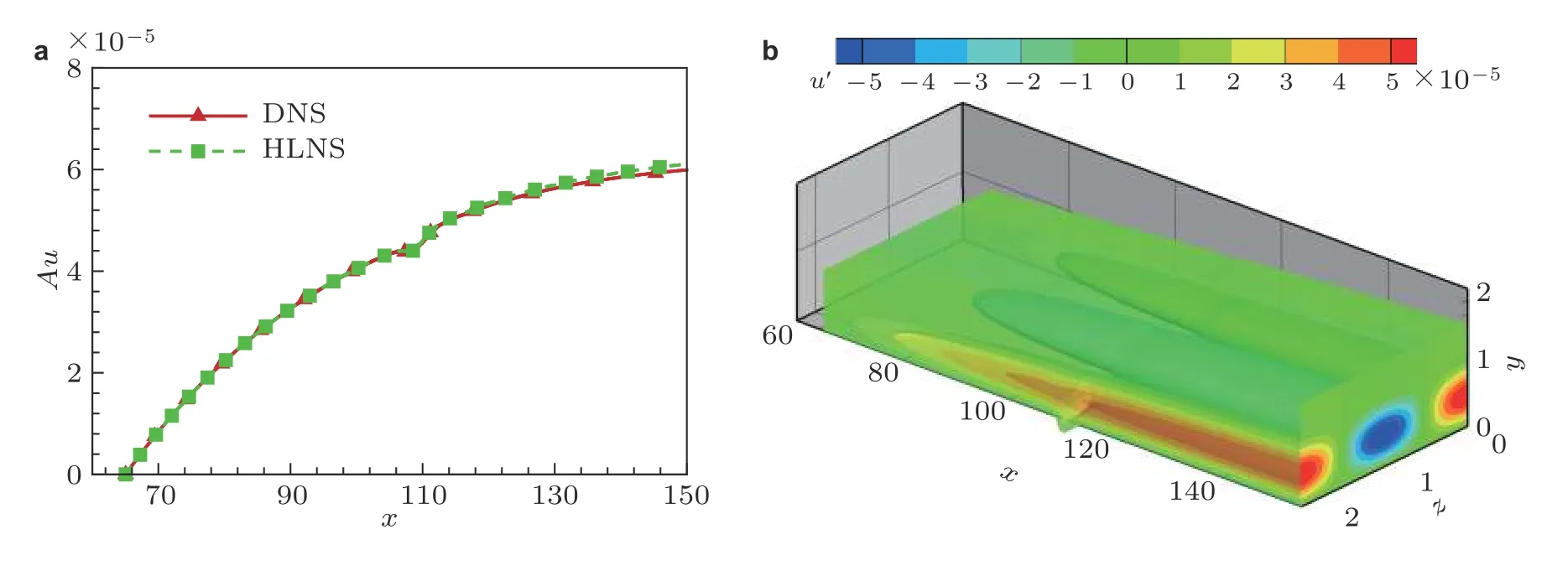
图 10 β =2.8(a)HLNS 与DNS 计算的凹槽作用下的幅值Au 对比,(b)及流向速度扰动的空间结构(H = 0.2,)
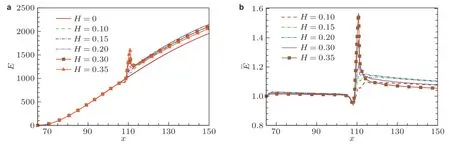
图 11 不同深度凹槽下的最优扰动的能量E(x)(a)以及归一化能量E¯(x)(b)沿流向的演化
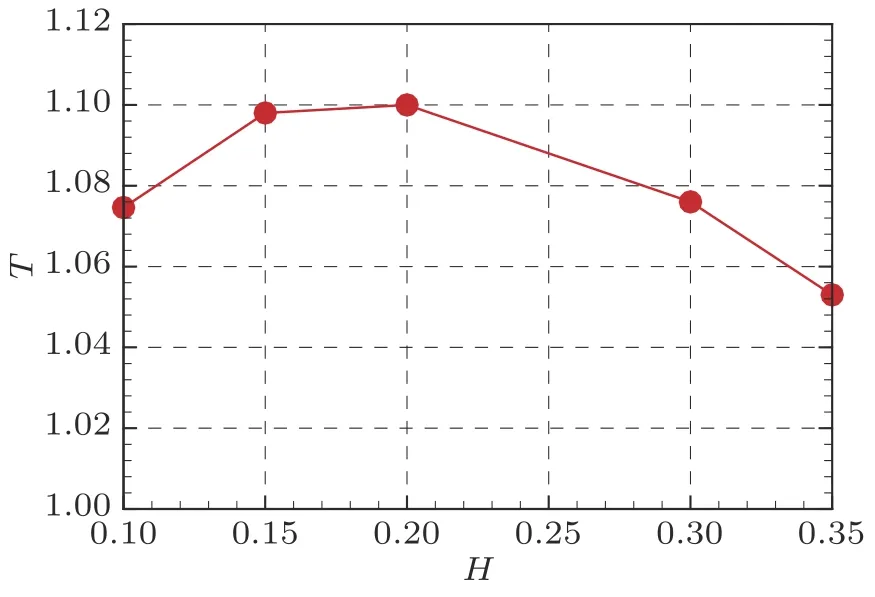
图 12 放大因子 T 随着凹槽深度H 的分布(β =2.8)
4 结 论
为揭示局部突变对非模态扰动演化影响的物理机理并发展定量预测方法, 本文基于HLNS及其系统, 发展了一套描述非模态扰动 (条带) 演化的最优扰动求解框架. 该框架保留了N-S 方程系统的椭圆性, 因而, 它不但适用于描述光滑壁面的条带发展过程, 还能描述条带在局部突变附近的快速畸变规律, 这是优于传统最优扰动求解方法 (Parades et al. 2016) 之处.
基于该方法, 本文研究了来流马赫数为5.96, 攻角为-4°的高超声速钝板边界层中局部凹槽对亚临界转捩的影响. 研究发现, 凹槽对非模态扰动的演化起促进作用, 且在本文所研究的参数范围内,H= 0.2 时的促进作用最大. 这与李强等 (2020) 风洞实验中发现的“凹槽促进转捩”的规律定性相符. 但是, 本文数值结果无法与实验结果做定量对比, 这是由于计算条件与实验条件仍存在一定差距. 首先, 实验上的凹槽形状是矩形的, 而本文为了计算方便, 对其进行了光滑处理; 其次实验中的凹槽宽度也比本文算例中的宽, 实验中三组凹槽的宽度与深度分别为 (2.5 mm,1 mm) 、 (3.75 mm, 1.5 mm) 、 (5 mm, 2 mm) , 由于条带的流向尺度很长, 更宽的凹槽更容易与条带作用. 另外, 除了条带本身的演化受到局部凹槽的影响以外, 其在发展到有限幅值以后激发的二次失稳模态也会受到凹槽的影响, 而这一机制并未在本文考虑.
附录A
基本流计算的网格无关性验证
为了验证计算的可靠性, 本文针对H= 0.2 凹槽工况的基本流计算开展网格分辨率研究. 将流向网格和法向网格分别加密一倍, 对比三套网格下计算的基本流剖面, 附图A1 给出了不同流向位置处的速度和密度沿法向的分布. 如图所示, 流向网格和法向网格加密后所得到的结果与原网格所得结果精确吻合.
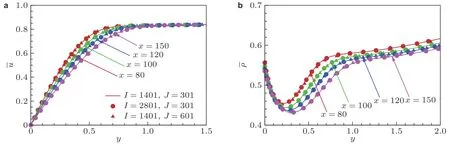
附图 A1不同网格数下的速度(a)、密度(b)剖面对比
致 谢本文受到国家自然科学基金的资助(12002235, U20B2003).

