基于大偏差理论非高斯随机动力系统离出行为研究

李 扬 赵 锋 刘先斌 ,*

1 南京理工大学自动化学院, 南京 210094

2 南京航空航天大学机械结构力学及控制国家重点实验室, 南京 210016

1 引 言

与非线性一样, 随机性也是客观世界的本质属性. 客观世界丰富多彩的复杂现象, 其成因通常是源于系统内禀的非线性、随机性及其之间的相互作用. 由于噪声样本的多样性及不确定性,受随机扰动的非线性系统所呈现的与原确定性系统截然不同的复杂且有趣的随机动力学行为一直是人们关注的焦点! 而其中, 受弱噪声扰动的系统动力学行为则更为有趣: 对于未受扰系统与受扰系统, 一方面, 在噪声充分弱的前提下, 人们会自然期待后者行为与前者充分接近 (依概率、概率1、均方意义等); 另一方面, 前者是确定性的, 其动力学行为由初始条件唯一确定, 而弱噪声是否会导致后者长期的随机动力学行为完全不同则更值得关注! 对此, 大偏差原理及其与之密切相关的离出问题研究给出了一个很好的回答. 与大数定律 (law of large numbers) 和中心极限定理 (central limit theorem) 不同, 这两者只关心大概率事件及其极限行为, “大偏差理论 (large deviation theory)” (Freidlin & Wentzell 2012) 则试图揭示“非线性随机系统中最初的小概率事件经长时间演化可成为大概率事件” 的机理. 这是因为受微扰系统行为对未受扰系统行为的大偏差在有限的时间内是小概率事件. 大偏差现象产生的原因在于, 概率理论中, 所谓一个“弱”随机扰动, 指的是其统计意义, 即: 扰动幅值很小的概率很大, 扰动幅值很大的概率很小, 且扰动的均值很小 (陈朕 2018).

数学上,粗略地说,大偏差理论源于一个事实:一族由实参数化的概率测度对于可测事件的估值呈现参数的指数变化率. 理论起源可追溯到北欧的精算师对保险行业风险估计研究——Cramér (1944) 的关于独立随机变量和一般的大偏差结果. Sanov (1957) 推导了独立同分布随机变量的经验分布. 随后, Donsker 和Varadhan (1975a, 1975b, 1976, 1983), Gärtner (1977) 将其推广至一般的Markov 链和Markov 过程. 而动力系统受弱随机扰动所产生的样本路径大偏差的结果最初由Varadhan (1967)、Ventsel 和Freidlin (1970)、Freidlin 和Wentzell (2012) 给出. 上述研究均基于一种广义Cramér 变换, 即通过选取参考测度, 使其对于所考察的事件具有大的概率测度,然后对于所考察的概率族建立关于参考测度的Radon-Nikodym 导数, 并进行估值 (Freidlin &Wentzell 2012; Wentzell 2012; Varadhan 1984, 2016; Deuschel & Stroock 2001; Dembo & Zeitouni 1998; Feng & Kurtz 2006). 20 世纪90 年代, Puhalskii, O’Brien 和Vervaat, Acosta 等通过类似于“基于Prohorov 紧性证明一族概率测度弱收敛”的方法, 将大偏差理论推广至样本路径左连续且具有右极限的随机过程类 (Varadhan 1984, 2016; Deuschel & Stroock 2001; Dembo & Zeitouni 1998; Feng & Kurtz 2006).

在随机动力系统中, 噪声诱导的大偏差现象会导致系统远离平衡态的复杂动力学行为, 即从稳态的吸引域中的离出现象. 离出现象是噪声诱导的非线性系统的全局动力学行为, 是非线性随机系统所特有的复杂现象! 在弱随机扰动下, 即使一个结构稳定的动力系统, 其受扰后的轨线可与未扰系统轨线之间产生大偏差并因此失去“结构稳定性” ! 一个即使只有渐近稳定平衡点的动力系统, 在非常弱的随机扰动下, 其长期作用的累积效应可使其样本轨线具有从吸引域中概率1的离出概率且可以到达任何有界的区域 (朱金杰等 2020, 刘先斌等 1996). 数学严格意义上, 反映确定性动力系统长期行为的非游荡点集、平衡点和极限环的稳定性、全局结构等概念已不再适用于随机系统, 因为此时相空间结构可能已面目全非. 而对系统随机动力学行为“如何偏差”以及“偏差发生的统计特征”等问题的探索便自然成为大偏差理论研究意义之所在 (Freidlin &Wentzell 2012, 朱金杰等 2020, 李扬 2021).

在离出问题中, 最优离出路径 (optimal exit path) 或称最大可能离出路径 (most probable exit path, MPEP)、平均首次离出时间 (mean first passage time, MFPT) 和离出位置分布 (exit location distribution, ELD) 是刻画系统“怎样离出” “何时离出”和“从哪离出”的三个重要的特征量,对它们的计算和分析一直是随机动力学领域的核心问题. Freidlin 和Wentzell (2012) 建立的大偏差理论从数学上为这个问题的解答提供了理论基础, 其核心思想在于, 定义了作用量泛函 (action functional) 的概念, 导出了轨道邻域小管道的概率的指数估计式, 从而将稀有事件的概率计算问题转化为泛函的变分问题. 基于经典力学的结果, 推导了最优离出路径满足的欧拉-拉朗格朗日方程 (Euler-Lagrange equation), 通过定义作用量泛函最小值为拟势 (quasi-potential), 同时证明了平均离出时间和离出位置分布与拟势的指数关系.

对于Markov 过程, MFPT 是停时 (stopping time) (Freidlin & Wentzell 2012, Bernt 2010)的均值. 它在诸多学科领域中都有其实际的应用价值, 如动力系统中衡量吸引子之间的相对稳定性(Kłosek-Dygas et al. 1988)、神经元自发性放电现象的峰峰间期 (interspike interval) (朱金杰2018, Ryashko 2018)、工程领域中结构的可靠性分析 (Chen & Zhu 2009, 2010)、生物学中基因的转录与翻译 (Bressloff 2017) 等. 针对MFPT 的研究由来已久, 最早可以追溯到20 世纪40 年代,Kramers (1940) 研究了朗之万方程 (Langevin equations) 的离出问题, 发现MFPT 与噪声强度的指数依赖关系. 针对拟可积哈密顿系统, 朱位秋等 (1992, 2017) 利用随机平均法研究了首次穿越时间和首次穿越失效的问题, 并以此刻画系统的可靠性. 此外, 胞映射作为一种有效的全局动力学行为分析方法, 也是计算MFPT 的有效数值工具 (徐伟等 2013). 另外, 许多研究者发现, 当MFPT 与系统内禀的或外在的时间尺度匹配时, 系统会产生类似于共振的行为, 如随机共振和自诱导随机共振等现象, 在机械系统和医学等领域都有重要的应用 (Kang et al. 2017, Zhang et al.2021, 王炜 2020, 颜志2021).

对于受高斯白噪声扰动的非线性系统, MFPT 方程v(x)=Exτ满足如下Pontryagin 方程 (狄利克雷边值问题) (Bernt 2010, Duan 2015)

其中A为生成元 (即Fokker-Planck 算子的伴随算子),D为待离出区域. 利用奇异摄动法和特征线法, Matkowsky 和Schuss 等 (1982, 1983, ) 及Naeh 等(1990)解析近似计算了在特征边界 (characteristic boundary) 和非特征边界 (non-characteristic boundary) 条件下的MFPT 渐进展开式. 基于van der Pol 变换、奇异摄动法和随机平均法, 孔琛和刘先斌 (2014) 计算了一类分段线性系统的MFPT, 发现分形边界会造成理论与数值结果的偏差. 之后, Kong 和Liu (2017) 利用广义图胞映射方法进行全局动力学分析以及结合随机平均法降维, 研究了受弱高斯白噪声扰动的分段线性系统的噪声诱导的混沌现象, 发现MFPT 可以作为“噪声诱导混沌”的指示器.

离出位置分布刻画了系统跨越边界时在边界上的离出点的分布情况, 同样是一个重要的物理量.对任意的连续函数f(x),函数u(x)=f(y)pe(x,y)dSy(pe(x,y)为离出位置分布) 满足方程

在弱高斯噪声条件下, Matkowsky 和Schuss 等 (1982, 1983,) 及Naeh 等(1990)利用奇异摄动法推导了离出位置分布的解析近似表达式. 针对高斯白噪声扰动的FitzHugh-Nagumo 系统,Chen 等 (2017) 发现模拟轨道离出位置与边界拟势最低点的偏差, 即鞍点回避现象(saddle point avoidance), 本质上来源于有限噪声强度的影响. 对于另一个可激系统, Li 等 (2020b) 同样揭示了鞍点回避现象, 并利用WKB 近似摄动计算了离出位置分布, 发现一阶修正能够弥补这个偏差.由于方程 (2) 的求解较为困难, 许多研究者设计了一系列计算离出位置分布的数值方法. 例如, 广义胞映射方法作为分析非线性系统全局动力学结构的有效工具, 同样能够用来计算离出位置分布 (Han et al. 2016). Zhu 等 (2018) 综合了正向通量采样 (forward flux sampling) (Allen et al.2005) 和快速Monte Carlo 模拟方法的优点, 提出了概率演化算法 (probability evolution method),能使用模拟方法快速得到离出位置分布.

最优离出路径的计算是最后也是最难的问题, 它旨在刻画离出发生的内在机理, 具有结构性的难度, 是大偏差理论的核心问题. 基于作用量泛函的变分, 最优离出路径满足欧拉-拉格朗日方程或对应的哈密顿系统. 此时, 哈密顿相空间相对于原确定性相空间扩展一倍. 若考虑具有稳定不动点的二维系统, 则确定性相空间作为不动点的二维稳定流形嵌入到四维拓展哈密顿相空间中. 由于噪声的加入, 不动点多出两个不稳定方向, 张成了二维不稳定流形, 即拉格朗日流形(Lagrangian manifold), 此流形到确定性相空间的投影构成离出路径的图案. 由于最优离出路径的解析计算比较困难, 众多研究者发展了大量的数值方法, 如action plot (Beri et al. 2005)、几何最小作用量方法 (geometric minimum action method, GMAM) (Heymann & Vanden-Eijnden 2008)、有序逆风法 (ordered upwind method, OUM) (Cameron 2012)、历程概率分布 (prehistory probability distribution) (Dykman et al. 1992) 和机器学习 (Machine Learning) (Li et al. 2021a) 等方法.

一般情况下, 若终点坐标在相空间中连续变化, 人们自然认为连接始末端点的最优路径也随之连续变化. 然而, 对于非平衡态系统, 情况却未必如此. Chen 和Liu (2016) 通过对周期激励双势阱系统的离出问题的研究, 发现最优路径可能随着终点的变化发生突变, 出现这种现象的根本原因在于拉格朗日流形出现折叠结构, 导致泛函极值的多值性和离出轨迹图案的奇异性. 在折叠的边缘——焦散线 (caustic) 处, 拟势的二阶导数发散, WKB 近似指数前因子也因此发散 (孔琛2018). 在折叠区域有一条明显的切换线 (switching line), 切换线两侧即使相距很近的两个点, 会有两条拓扑性质完全不同的最优路径到达. 在切换线上, 拟势不可微. Chen 等 (2019) 研究了Type-I 和Type-II 可激性条件下的Morris-Lecar 系统, 揭示了拟势的非可微性、最优路径的非光滑性和拉格朗日流形的奇异性的联系, 同时发现最优路径满足的非光滑向量场会出现闭轨, 本质上是非光滑系统的擦切分岔所产生的擦切环, 或由滑移分岔产生的滑移环.

另外, 离出问题中某些奇异现象的出现来源于动力系统本身的复杂结构, 如混沌现象和分形边界等. 针对非双曲混沌吸引子的离出问题, 最新研究 (Chen et al. 2016) 发现其离出过程是沿着一个异宿轨道的交叉层次结构进行的, 噪声不断地将离出轨迹从当前鞍型周期轨道的不稳定流形扰至包含其上一层不稳定流形, 而离出轨迹在不稳定流形上的每一次跃迁都伴随着噪声的一次剧烈波动. Kraut 和Feudel (2003) 研究了吸引域中存在混沌鞍的Ikeda 映射的离出问题, 发现在混沌鞍上拟势几乎水平, 由此极大降低了离出所需的能量. 还有一些学者研究了具有局部不连通 (locally disconnected) 和局部连通 (locally connected) 分形边界的连续和离散动力系统的离出问题, 发现离出总是发生于唯一的可达边界点 (accessible boundary point) 上 (Silchenko et al.2005).

目前, 除了涉及混沌系统的复杂离出机理和离出路径的拓扑奇异性问题之外, 有关高斯噪声离出问题的结果相对较为完善. 而关于非高斯随机系统的研究则较为匮乏, 近年来逐渐成为离出问题研究的焦点之一. 事实上, 相比高斯扰动, 自然界中的大量涉及跳跃、突变、间歇、爆破、跃迁等客观现象, 如基因突变、火山爆发、能级跃迁等, 更适合利用具有非高斯噪声的随机动力系统建立模型 (Duan 2015, 李扬2021). 因此, 非高斯随机动力系统是具有深刻科学意义的现象学模型, 相关的离出问题的研究不仅对于随机动力系统理论具有推动作用, 更有着重要的实际应用价值.

非高斯扰动往往涉及噪声样本的跳跃特性, 目前研究较多和应用广泛的非高斯随机系统主要有三种. 第一种是随机混合系统 (stochastic hybrid system), 即连续变量与离散变量耦合的过程. 控制连续变量演化的方程的向量场依赖于离散变量, 离散变量是转移率依赖于连续变量的跳跃Markov 过程, 因此两者构成耦合随机过程. 第二种是具有指数轻跳跃扰动 (exponentially light jump fluctuation) 的随机动力系统, 这种噪声是Lévy 噪声的一种, 其跳跃测度 (jump measure) 指数衰减. 第三种非高斯噪声也是Lévy 噪声的一种, 即α稳定Lévy 噪声, 其跳跃测度多项式衰减.本文第二节引入大偏差理论的基本思想, 第三、四、五节分别介绍三种常见非高斯随机系统的离出问题的主要处理方法和近期研究进展, 并在最后一节提出一些开放性问题.

2 大偏差理论构建

2.1 大偏差理论基本思想

在非线性动力学中, 人们往往更加关注极限行为, 如平衡点、极限环和奇怪吸引子等不变集结构. 类似地, 众所周知的大数定律和中心极限定理是概率理论中有关极限行为的两个主要结果. 直观上, 对于类型的随机动力系统,ξt为给定的随机扰动,ε为小的噪声强度,ε=0对应确定性系统t=b(xt),大数定律给出了扰动系统的解在有限时间内对于未受扰轨道xt的依概率收敛性结果, 中心极限定理则进一步断言一阶近似依分布收敛于正态分布.

与大数定律和中心极限定理不同, 这两者只关心未受扰轨道附近的大概率事件, 而大偏差理论则反其道而行之, 它关注稀有事件 (rare events), 如噪声诱导的从吸引域中的逃逸现象 (Maier &Stein 1992, Li & Liu 2019)、噪声诱导的不同稳态之间的转移 (Li et al. 2020a, Chen & Liu 2017)、神经元系统跨阈值放电现象 (Khovanov et al. 2013, Li et al. 2020b, Chen et al. 2017)、噪声诱导的混沌 (Tamás & Lai 2010, Kong &Liu 2017) 等, 均属大偏差理论的应用范畴. 在有限时间内, 大偏差现象发生的概率很小, 这样深度挖掘极度稀有的事件似乎与概率论的宗旨相悖, 因为似乎大概率事件对预测事物演化更具启发式意义. 然而, 若将时间尺度延至无穷, 小概率事件长期的累积效应将可能逐渐演化为大概率事件. 因此, 在有限时间内精细区分出哪些事件是“更不可能的(more improbable)”, 哪些事件是“稍不可能的 (less improbable)”, 成为揭示无限时间尺度下概率1 的大偏差现象本质机理的一把钥匙.

数学上, Freidlin-Wentzell (2012) 大偏差理论建立了随机动力系统的解穿过一个给定路径φt的邻域的概率估计式

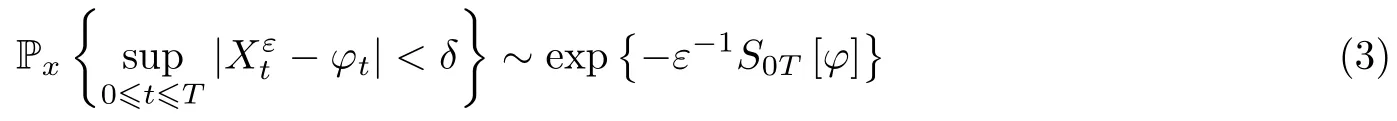
其中S0T[φ]=即为引言中提到的作用量泛函,L为拉格朗日量, 其形式取决于所研究的随机过程 (扩散过程、随机混合系统等), sup|·|记为上确界范数,δ是一个正的小参数, Px的下标为初值=φ0=x. 由于单条路径的概率必然为零, 为了对比不同路径实现的可能性, 式 (3)利用轨道附近小邻域的概率代替原轨道的概率. 根据Laplace 方法, 诸多事件的概率均取决于此泛函的约束最小化, 例如B为Rn的某一Borel 子集, 则∈B的概率对数等价于exp( inf表示下确界). 因此, 大偏差理论的精辟之处在于, 它将概率的复杂计算问题转化为作用量泛函的约束最小化问题, 从而可以利用分析力学和变分学的经典结果进行求解.

根据变分原理, 作用量泛函的驻值解-最优离出路径, 满足欧拉-拉格朗日方程

或对应的辅助哈密顿系统

其中哈密顿量H是L的Legendre 变换. 尽管离出路径的众多样本是随机的, 然而它以压倒性的概率落在最优路径附近, 且ε →0时, 它依概率收敛于最优路径. 大偏差理论的结果使得随机动力学的某些复杂行为变得近乎可预测! 在离出问题中, 最优路径的研究始终是一个结构性的难题. 分析最优路径的结构对于理解噪声在离出问题中的作用至关重要, 是随机动力学的核心问题之一.

2.2 拟势

如引言所述, 平均离出时间和离出位置分布均指数依赖于作用量泛函的最小值, Freidlin 和Wentzell (2012) 将其定义为拟势. 具体来说, 拟势具有如下形式

其中φ ∈(0,T)表示φ(0)=,φ(T)=x,记为绝对连续函数集. 换句话说, 拟势是连接初始位置和终点位置x之间所有绝对连续函数的作用量的最小值, 且要求对轨迹和时间都取最小. 通常, 初始位置选为稳定不变集 (如稳定不动点O), 此时可将拟势V(O,x)简记为V(x). 对于多稳态的系统, 需要先计算出每个稳态的吸引域拟势, 然后将几个区域的拟势拼接起来, 得到全局范围的拟势.

针对简单的加性高斯噪声的情况, 拟势的意义可以按下述方式理解. 首先, 假定向量场b(x)具有如下的分解

其中连续可微函数U(x)满足U(O)=0(O为D中的稳定平衡点), 对x/=0有U(x)>0且∇U(x)/=0,(l(x),∇U(x))=0.则系统关于点O的拟势V(x)满足V(x)=2U(x) (Freidlin & Wentzell 2012). 若U(x)是二次连续可微的, 则从O到x的最大可能路径φs,-∞≤s≤T, 满足下面的方程

对比方程 (8) 和原始确定性方程后发现, 在噪声的驱动下, 离出路径保持旋转分量l(x)不变,仅仅将向内的法向分量-∇U(x)翻转向外, 使得噪声能够消耗尽可能小的能量驱动系统离出. 若考虑有势系统, 即旋转分量l(x)=0,则拟势与势函数U(x)仅仅相差一个常数因子. 换句话说, 在有势系统中, 拟势与势函数完全等价. 即使在非有势系统中, 拟势仍然可以看成是广义的势函数.这也是拟势这个名称的来源.

通常, 对向量场进行线性化并计算特征值或最大李雅普诺夫指数 (largest Lyapunov exponent) 是最常见的系统稳定性分析方法. 特征值取决于势函数的二阶导数, 刻画了系统离开不动点邻域的难易程度, 因此可以理解为系统离出时“爬得多陡”. 然而, 这种方式只能刻画系统的局部稳定性, 无法展现涉及全局结构的信息. 在随机扰动下, 系统从不动点的整个吸引域中的离出行为是许多动力学问题的核心, 而局部稳定性显然不足以刻画此类问题. 另一种稳定性是根据吸引域半径的长度来定义, 即考察系统“走得多远”. 这种定义方式在某些情况下非常适用, 例如噪声强度较大时的跳跃噪声. 尽管这种稳定性是比前一种更加全面的全局稳定性, 在一定程度上能够刻画平衡点的稳定范围, 然而单纯以吸引域大小定义稳定性仍有一定的局限性. 例如, 定义在区域[-1,1]上的两个分别具有势函数U1(x)=x2与U2(x)=0.01x2的系统, 尽管稳定区域一致, 两个系统的稳定性明显不同, 相应的离出难度也不一样. 这就涉及第三种稳定性的定义方式, 即从能量的角度考察离出需要越过的势垒高度, 在物理化学系统中称为活化能, 可以理解为“登得多高”(朱金杰等 2020). 在大偏差理论中, 拟势扮演了这样一个势垒的角色, 在有势系统中, 它也能与势函数重合. 因此, 拟势的概念从能量的角度为吸引子的全局稳定性提供了一种定量判据, 从而噪声诱导的不同稳态之间的转移现象转化为不同拟势势阱的跃迁行为.

3 随机混合系统研究进展

生物系统中的噪声依据来源可以分为两类, 以神经元系统为例, 可以分为固有噪声 (intrinsic noise) 和外在噪声 (extrinsic noise) (Bressloff & Newby 2013). 后者来源于环境因素, 主要由突触输入的持续性冲击构成, 相关的系统一般模型化为基于郎之万方程的连续Markov 过程. 而固有噪声产生于有限个离子通道的随机开闭, 具有明显的离散特性, 一般模型化为跳跃Markov 过程.一般地, 若x(t)表示连续的突触变量,n(t)∈{0,1,2,··· ,K}为离散的开通道数, 只考虑固有噪声的情况下,x(t)在n(t)两次跳跃之间满足确定性方程

其中τ为突触时间常数, 而n(t)的演化服从转移率为Wnn′(x)/τn的跳跃Markov 过程n′ →n, 因此[x(t),n(t)]构成耦合Markov 过程, 称为分段确定马氏过程 (piecewise deterministic Markov process), 或随机混合系统 (stochastic hybrid system) (Bressloff & Newby 2014). 为了简化, 这里考虑连续变量是一维的情况. 除了神经元模型外, 它在物理化学、分子动力学、基因转录等领域都有着重要应用 (Assaf et al. 2011, Newby 2014a).

对于这个耦合系统, 引入对应的概率密度pn(x,t)

则概率密度的演化服从微分形式的Chapman-Kolmogorov (CK) 方程

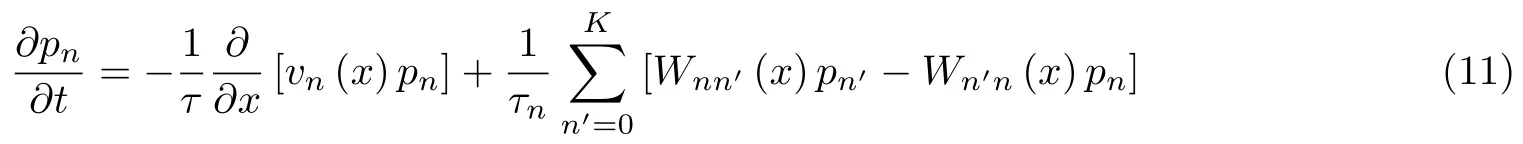
注意, 在这个系统中引入了两个时间尺度, 弛豫时间尺度τ和转移时间尺度τn. 一方面, 若考虑极 限τ →0,根据式 (9) 得到vn(x)=0,则x为依赖于n的常数, 从而概率P(n,t)=P{n(t)=n}的演化控制方程转化为

即跳跃Markov 过程. 若n(t)每次只跳跃一步, 即n →n±1, 则系统简化为更为人们所熟知且应用更广泛的生灭过程 (birth-and-death process) (Dykman et al. 1994), 即

其中边界条件为P(-1,t)=0,P(K+1,t)=0.令Ω±(n/K)=ω±(n)/K,x=n/K, 结合方程 (13),当K →∞时得到确定性方程

另一方面, 在诸多实际的生物物理模型中, 跳跃过程的动力学远快于连续变量的弛豫行为,即τn ≪τ(Bressloff & Newby 2014). 因此, 令τ=1,τn=ε, 可以将方程 (11) 改写成另一种更加紧凑的形式

在ε →0极限下, 式 (15) 约化为确定性方程或称平均场方程 (mean field equation)

其中ρn(x)是满足Anm(x)ρm(x)=0唯 一的平稳分布. 这里假定, 对固定的x, 矩阵A(x)是不可约的.

注意到当前者K →∞或后者ε →0时, 这两种系统分别收敛于对应的确定性系统. 换句话说,1/K和ε分别刻画了它们的噪声强度. 在K较大或ε较小的情况下, 许多学者研究了这两种系统中弱噪声诱导的扰动系统与未受扰系统之间的大偏差现象及相关的复杂随机动力学行为. 下面两子节分别介绍这两种系统的研究进展.

3.1 生灭过程

考虑上述生灭过程 (13), 写成关于x的密度形式如下

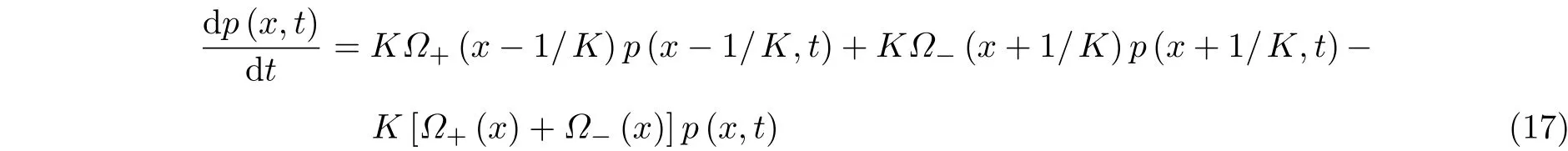
此处KΩ+(x) (KΩ-(x))表示x跳跃至x+1/K(x-1/K) 的转移率. 对于任意光滑函数f(x), 上述过程的无限小生成元为

给定任意初始分布, 上式唯一定义了一个跳跃Markov 过程. 一个非常有趣的问题是: 当K →∞时, 该Markov 过程具有怎样的极限行为?

事实上, 当K →∞,O(1/K)阶次的跳跃步长意味着上述过程逼近其连续极限, 而O(K)阶次的转移率说明系统关于时间快速变化, 系统将快速收敛至其唯一的平稳不变分布. 与此同时, 若系统具有某种遍历性特征, 则这种“快速震荡”使得该Markov 过程的轨道呈现出大概率集中于其“平均系统”, 而小概率发生偏离的现象. 这一现象可由大偏差原理解释.

令H(x,β)=Ω+(x)(eβ -1)+Ω-(x)(e-β -1),L(x,α)=(αβ-H(x,β))为H(x,β)的Legendre 变换. 记为上述过程以x0为起始点的概率分布, 则根据大偏差原理 (Freidlin & Wentzell 2012), 有

由于H(x,0)=0,可以推得L(x,α)≥0.同时L(x,α)=0当且仅当α=Ω+(x)-Ω-(x), 立即有推论

即, 当K →∞,在O(1)时间尺度, 系统大概率沿着确定性轨线运动. 这实际上是大数定律的结果,该确定性运动正是上述“快速震荡”导致的系统平均动力学行为. 大偏差理论相比于传统大数定律和中心极限定理的优越性在于, 它使得系统相对于其确定性平均的有限偏差的指数小概率可以得到估计, 并可以应用于研究系统长期动力学的渐近行为. 如系统的转移概率PK(t,x0,x)取决于V(t,x0,x)=,平稳概率分布(x)由拟势V(x)支配, 平均离出时间近似具有exp(KC)阶次, 而常数C由拟势确定. 这些结果与扩散情形一致, 此处不再阐述.

一个有趣的现象是, 当K →∞且t →∞时, 系统在不同的时间尺度呈现不同的动力学行为.如先有K →∞再有t →∞,此时xK(t)大概率趋于初值x0的ω极限集; 而若先有t →∞再有K →∞,系统呈现位于所有极限集上的集中分布; 而当t ～exp(KC), 如前所述, 系统呈现有界区域的离出行为 (Schuss 2009). 那么, 在其他时间尺度, 随机系统又有怎样的行为呢?

令x(t)为任意一条确定性平均系统的轨线, 可以证明标准偏差K1/2(xK(t)-x(t))在任意有限时间区间弱收敛于高斯扩散过程ξ(t), 其对应的无限小生成元为

这实际上是中心极限定理类型的结果 (Ge & Qian 2011). 取x(t)=为确定性系统的稳定平衡点,由ξ离出O(1)区域的时间近似是O(1)阶的可知,xK(t)相比于的O(K-1/2)偏差发生在O(1)时间尺度.

进一步, 考虑偏差ηK(t)=Kγ(xK(t)-x(t))=(xK(t)-x(t)),0＜γ ＜1/2, 有

同样地, 取x(t)=为确定性系统的稳定平衡点, 由ηK(t)发生O(1)偏差的时间近似是O(exp(K1-2γC))阶次的可知,xK(t)相比于的O(K-γ)偏差发生在O(exp(K1-2γC))阶时间尺度.

相似的结果可以推广至高维. 考虑状态空间为εZn(Z为整数集) 的连续时间跳跃Markov 过程, 其生成元为

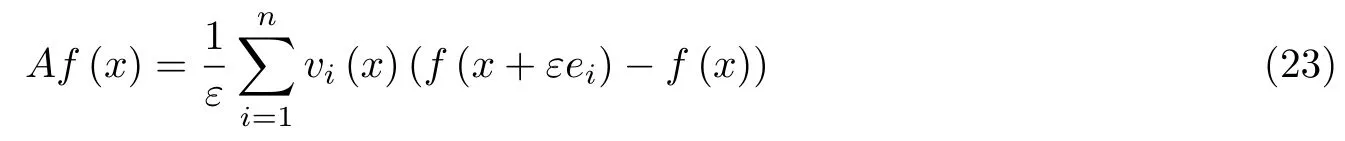
利用与一维情形相似的推导过程, 上述结论可自然在高维进行推广, 此处不再赘述.

3.2 随机混合系统

随机混合系统在神经元模型、分子动力学、基因转录等领域都有大量的应用 (Assaf et al.2011, Newby 2014a, Li & Liu 2019). 其连续变量和离散变量耦合的特殊结构, 既能模型化一大类实际物理系统, 同时也带来了高度的复杂性. 尽管扰动一般较弱, 即ε通常较小, 长期作用下离出行为仍十分普遍. 为此, 众多研究者分析了随机混合系统的大偏差现象, 设计了多种解析与数值方法, 并得到了一系列引人注目的结果. 例如, 一些研究者利用摄动法近似计算了基因调控和离子通道等模型的平均首次离出时间 (Bressloff & Lawley 2017). 基于WKB 近似和路径积分公式,Bressloff 和Newby (2013, 2014) 推导了随机混合系统的作用量泛函和最优离出路径满足的辅助系统, 计算了随机混合神经网络系统的离出路径和离出时间, 分析了随机混合Morris-Lecar 系统离出路径的奇异性结构. 分析发现, 类似于扩散过程的情况, 随机混合系统的最优路径仍然满足哈密顿系统. 然而, 区别在于, 哈密顿量由一个符号矩阵的特征值提供, 而作用量泛函为哈密顿量的Legendre 变换 (即拉格朗日量) 的积分, 因此作用量泛函与哈密顿量一般无法给出显式形式,这为问题的求解带来了极大的困难与挑战. 为此, 许多研究者提出了诸多近似方法, 如拟稳态扩散近似 (quasi-steady-state diffusion approximation, QSS), 绝热近似 (adiabatic approximation), 系统尺寸扩展 (system-size expansion) 等方法 (Bressloff & Newby 2011, Brooks & Bressloff 2015,Keener & Newby 2011), 试图利用扩散过程近似随机混合系统. 这些方法对于捕捉系统的高斯型涨落以及揭露拟环 (quasi-cycle) (Brooks & Bressloff 2015) 的出现等局部性质具有突出的优越性.然而, 在考虑亚稳态 (metastability) 现象时, 拟势和最优路径会出现不可接受的误差 (Li & Liu 2019).

下面引入一些典型的随机混合系统的理论和数值方法, 如扩散近似方法中最常用的QSS, 处理大偏差问题的WKB 近似, 并介绍近期发展的重要结果.

3.2.1 拟稳态扩散近似

假定ε很小, 则内部变量n的 转移率充分大, 使得n快 速跳跃的同时x的变化很小. 这个结果表明, 系统位于状态n的概率快速收敛于ρn(x). 这一事实引出了QSS 方法的基本思想, 即, 概率密度pn(x,t)可以近似分解为给定x的状态n的平稳分布ρn(x)与x的边际分布的乘积 (Bressloff & Newby 2014). 具体来说, 假设概率密度为

代入微分CK 方程 (15) 中, 并利用摄动法得到C(x,t)的演化满足的FPK 方程

其中漂移系数和扩散系数分别为

Zn(x)是满足条件Zn(x)=0, 且是方程(28)的唯一解

注意在这里只保留了FPK 方程 (26) 的漂移与扩散的最低阶项. 函数C(x,t)表示近似的扩散过程的概率密度函数. 由此可以利用扩散过程 (26) 近似原先的随机混合系统, 从而使系统简化.

实际上, QSS 扩散近似方法的优势主要在于二维情况下能够捕捉到不动点附近的高斯型涨落. 具体来说, 考察平均场方程处于接近超临界Hopf 分岔点的情况, 系统存在一个稳定的焦点,雅可比矩阵具有一对复共轭特征值. 此时确定性流表现为暂态振荡模式, 衰减率为特征值实部.而当存在固有噪声时, 即对于随机混合系统, 暂态振荡转化为长期的大振幅振荡, 对应的功率谱出现一个峰值, 称为拟环 (quasi-cycle) 现象. 通过QSS 方法计算出近似的Itô随机微分方程, 在不动点处线性化后经过Fourier 变换可以得到系统的功率谱. 近似结果得到的功率谱会出现一个峰值, 与原随机混合系统的模拟结果相当吻合 (Bressloff 2010, 2017; Brooks & Bressloff 2015). 因此,QSS 方法对于拟环现象的分析具有显著的优势.

以单集群随机混合神经网络模型 (Li & Liu 2019) 为例, 讨论QSS 扩散近似方法的应用. 对于此模型, 连续变量x代表总的突触电流, 离散的内部变量n表示激活的神经元个数.n(t)的演化服从一个转移率为Ω±(x,n)/ε的单步跳跃Markov 过程

其中Ω+=n(t),Ω-=F(x).F是Sigmoid 激活率, 定义为

其中F0,Γ和θ分别为速率常数, 增益和阈值. 突触电流x(t)满足分段确定方程

则系统的概率密度pn(x,t)满足的CK 方程形式为

其中的矩阵A(x)满足

通过计算, 平稳分布ρn(x)满足参数为F(x)的泊松分布, 则可得到平均场方程

平均场方程关于参数θ的分岔图如图1 所示,θ=0.95时,存在两个稳定不动点x1,x2和一个不稳定不动点x0.

图 1 平均场方程关于 θ从单稳态到双稳态的分岔图.θ =0.95时,存在两个稳定不动点 x1, x2和一个不稳定不动点x0

其中ξt是一个高斯白噪声, 漂移系数f(x)是由式 (34) 定义的平均场方程的向量场, 扩散系数满足D(x)=w2F(x).

若要考察系统的离出现象, 则根据人们所熟知的扩散过程的大偏差理论的结果, 易得拟势VFP(x)满足哈密顿雅可比方程 (李扬2021)

根据经典力学的结果, 这个方程可以沿着下面的参数化轨道进行积分求解

事实上, 对于此一维模型, 拟势可以直接通过式 (36) 求解得到

当然, 后面会看到, 扩散近似后的大偏差结果相对于原混合系统, 在远离不动点处会出现较大的误差.

3.2.2 WKB 近似

如前文所述, 尽管扩散近似在捕捉不动点邻域内的高斯型涨落等局部性质时具有突出的优越性, 然而, 当考察离出问题等全局现象时会出现不可接受的误差. 此时, 直接对原随机混合系统应用WKB 近似方法是十分必要的.

一般地, 假设CK 方程 (15) 的平稳概率密度满足下面的WKB 形式

其中V(x)为拟势,Rn(x)是给定x的状态n的条件分布.pn(x)的值主要取决于指数项,N为前因子函数, 由ε的更高阶的齐次方程决定, 这里不做讨论. 将方程 (39) 代入CK 方程的时齐版本并合并ε的最低阶项得到

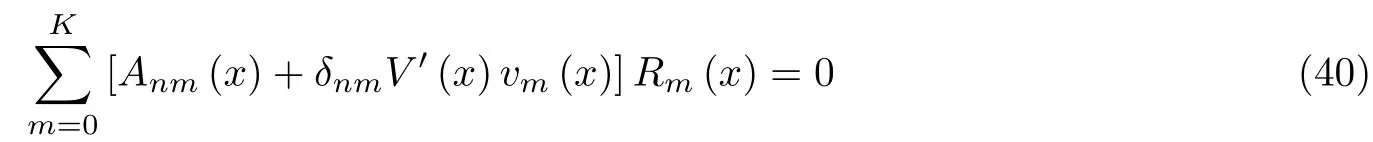
其矩阵形式为

众所周知, 在弱噪声极限下, 扩散过程对应的拟势满足哈密顿雅可比方程. 类似地, Bressloff和Newby (2014) 证明了随机混合系统的拟势满足下面的哈密顿雅可比方程

其中,λ0是矩阵Q的主特征值, 称为Perron 特征值. 它是实的单特征值, 并且大于所有余下的特征值的实部. Perron-Frobenius 定理保证了它对应的特征向量是严格正的. 因此, 最优离出路径满足辅助哈密顿系统

沿着这些极值路径, 拟势的演化满足

可以看出, 随机混合系统的哈密顿量一般没有解析表达式, 因为它是一个符号矩阵的主特征值. 这正是随机混合系统复杂性的根源所在. 因此, 用随机微分方程逼近随机混合系统的QSS 等方法就显示出它们的重要意义.

事实上, 由方程 (41) 的解决定的哈密顿量的选择并不唯一. 例如, 它也可以定义为(x,p)=det(Q)(Newby 2014b). 尽管这个定义有一定的优势, 即哈密顿量总能写出解析表达式,但它有一个缺点, 即这样定义的哈密顿量不是动量p的凸函数, 而凸函数性质是处理更高维问题的几何最小作用量方法 (Heymann & Vanden-Eijnden 2008)、有序逆风法 (Cameron 2012) 等数值方法所需的本质特性. 尽管如此, 可以证明H和具有相同的极值路径, 只是时间参数化不同(Newby 2014b). 一般地, 将系统的哈密顿量取为Perron 特征值.

上一子节的随机混合神经网络模型是少有的能够解析计算出哈密顿量的例子. 应用WKB近似方法, 通过将Rn(x)假设成Poisson 分布的形式, 根据方程 (41), 可推导出哈密顿量 (Li &Liu 2019)

最优离出路径和拟势可以通过积分对应的常微分方程组 (43) 和 (44) 得到.

根据式 (45), 零值哈密顿量分别导出两条零能量轨道, 即对应于p=0的弛豫轨道和对应于p=1/w-F(x)/x的活化轨道, 如图2 所示. 容易看出, 每条最优路径都是连接不动点和鞍点的异宿轨. 如果p=0, 可以发现辅助哈密顿系统 (43) 约化为平均场方程, 因此系统在弛豫轨道上运动不需要能量. 这表明动量实际上度量了最优路径和确定性路径之间的距离. 因此, 类似于扩散过程, 动量p的值可以看成是反映噪声影响的指示器. 然而, 系统在活化轨道上的运动需要克服稳定不动点的吸引性, 能量当然是需要的, 大小为

图 2 哈密顿系统的相图和离出路径.粉色和亮蓝曲线分别代表从 x1到x2和x2到 x1的离出路径.绿色和棕色虚线表示扩散近似的离出路径

如前所述, 若考虑噪声诱导的离出现象, 则随机混合系统与其扩散近似的结果相比有显著的偏差, 如图3(a)所示的拟势. 对于亚稳态问题, 这种偏差即使很小, 也会导致QSS 方法的失效. 其原因是, 拟势出现在MFPT 的指数项中, 因此拟势的微小差异将导致MFPT 的较大误差. 通过Monte Carlo 模拟 (Li & Liu 2019), 针对不同的噪声强度, 计算出从右边不动点穿过鞍点的MFPT,如图3(b)所示. 利用MFPT 的对数与拟势、噪声强度的倒数成正比的事实, 可以很容易地得到MFPT 的对数与噪声强度倒数的函数关系. 在图3(b)中, 拟合直线的斜率代表了拟势的大小, 约为0.097 8, 这与原系统的WKB 近似结果0.0964 一致, 而与QSS 给出的结果有很大差异.

Li & Liu (2019) 给出了QSS 方法失效的原因. 通过对比扩散近似前后的两个哈密顿量H(x,p)=-xp+wp·F(x)/(1-wp)和(x,p)=[-x+wF(x)]p+w2F(x)p2,容易发现(x,p)恰好是H(x,p)关于动量p的二阶近似. 因此, 在不动点或鞍点邻域内,H(x,p)和(x,p), 以及它们对应的离出轨道, 吻合地很好. 在图2 中, 动量p关于坐标x的曲线的斜率代表拟势的二阶导数. 基于此, 可以发现, 在不动点邻域, 有效FPK 和原系统的结果几乎是重合的. 这一特殊事实意味着,QSS 前后计算的拟势关于x的二阶以内是一致的. 然而, 在相空间的其他区域, 由于动量很大, 哈密顿量的二阶近似是不够精确的. 事实上, 正是远离不动点处的较大的动量推动系统克服了不动点的吸引力, 使稀有的离出事件得以实现. 这就是QSS 失效的原因. 值得注意的是, FPK 方程的解所提供的哈密顿量必然是动量p的 二次函数, 而矩阵Q的Perron 特征值一般不会正好是这种形式. 鉴于此, 当考虑离出事件时, 扩散近似的失效是自然的.

图 3 (a)扩散近似和原始系统的拟势对比,(b)平均离出时间的对数和噪声强度的倒数之间的关系

图 4 细致平衡条件分析示意图

3.2.3 细致平衡条件

细致平衡 (detailed balance) 原是物理学中的一个概念, 由van Kampen (1957)、Graham 和Haken (1971) 独立地应用于FPK 方程. 粗略地说, 一个马尔可夫过程, 如果在平稳情形下, 每一个可能的状态转移都与其逆转移平衡, 那它就处于细致平衡. 细致平衡现象与大偏差问题具有密切联系, 若系统处于细致平衡, 则从稳态涨落到某一点的最优离出路径与该点在无噪声情况下弛豫到稳态的确定性轨迹完全重合, 只需将时间反向. 因此, 离出路径构成的拉格朗日流形的奇异性也不会出现, 问题得到了极大地简化.

表1 中列出了几种典型随机过程的细致平衡条件. 众所周知, 对于加性高斯噪声的具有势函数的随机微分方程, 细致平衡自动成立. 对于其他情况, 朱位秋 (1992) 给出了扩散过程处于细致平衡时漂移和扩散系数需要满足的条件, 并以此可得到系统的平稳势, 从而能够求解平稳FPK方程. 对于一般的齐次Markov 过程, 在满足若干假设下, Gardiner (1985) 推导了此类过程微分形式的CK 方程, 并利用其系数导出了此过程满足细致平衡的充要条件. 基于此, Dykman等 (1994) 证明了跳跃Markov 过程的细致平衡条件为WjiPi=WijPj.

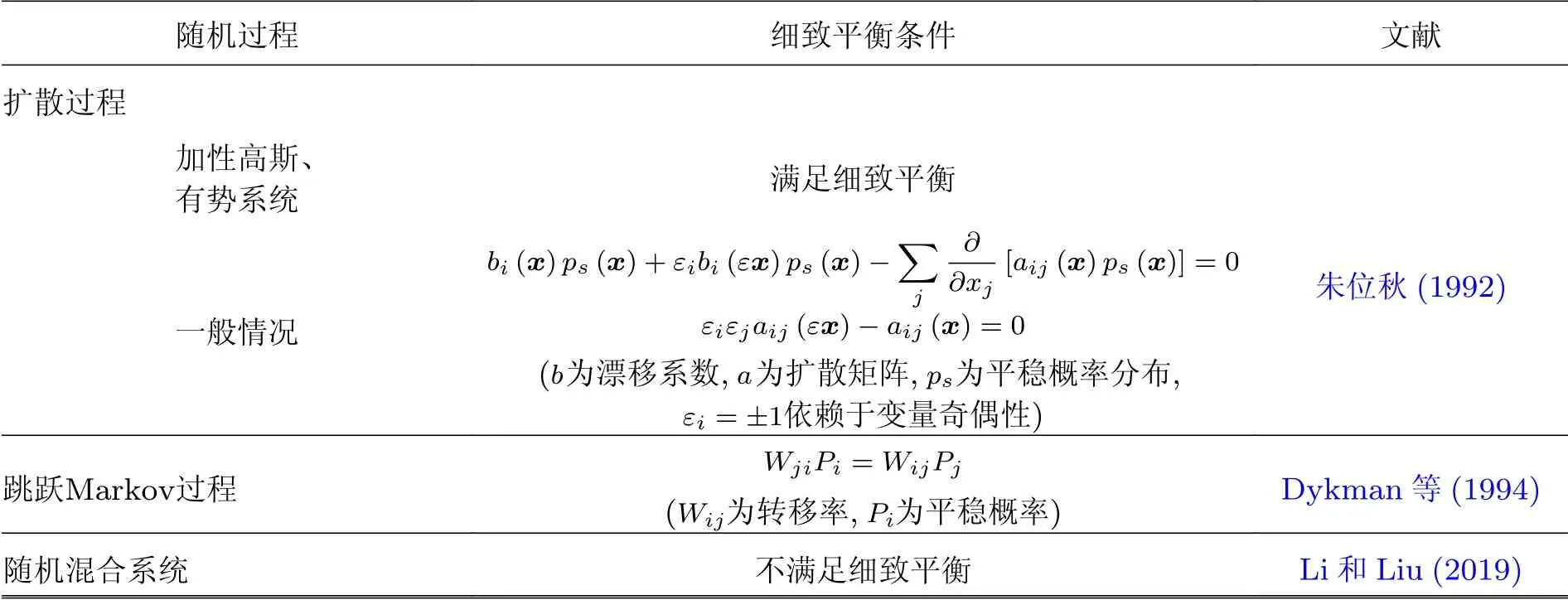
表 1 几种典型随机过程的细致平衡条件

对于随机混合系统, Li 和Liu (2019) 证明了此类过程必然不满足细致平衡. 数学上, Gardiner(1985) 推导的齐次Markov 过程处于细致平衡的充要条件在随机混合系统的情况下约化为

根据第一个方程, 得到vn(x)=0.存在两种可能: 一方面, 若vn(x)与x无关, 则可解出状态n为某个常数, 即状态n不存在转移, 此时离散变量已不再是随机的, 这时系统已不再是随机混合系统. 另一方面, 若vn(x)与x相关, 则可得到x=f(n), 意味着一个连续变量等于一个离散变量. 显然, 这个事件概率为零. 综上, 随机混合系统必然不满足细致平衡.

前面的解释是由数学语言给出的, 然而怎样才能直观地理解这种奇特的现象呢? 如图4所示, 假设系统在时刻t跳到状态n, 然后它会在状态n上停留一个正随机时间τ(τ=0的概率为零), 然后它将跳到另一个状态. 在这个时间间隔内, 系统沿着由x˙=vn(x)定义的确定轨迹移动.假设系统起始于(n,x),在充分小的时间区间 Δt内,系统从状态n跳跃到其他状态的概率为CΔt, 留在状态n的概率为1-CΔt.因此, 若vn(x)不等于零, 则转移概率

然而, 若系统起始于状态x+vn(x)Δt,在n保持不变的情况下, 系统在 Δt时间之后不可能到达状态(n,x),这是因为x˙=vn(x)是确定性方程, 而相轨迹不可能与自身相交. 因此,n必须在 Δt时间区间内跳跃数次才能抵达状态(n,x). 鉴于随机轨道精确到达某一点的概率必然为零, 因此转移概率

于是, 正向与反向的运动概率不可能相等, 除非vn(x)=0. 这与前面的分析一致, 即对于随机混合系统, 时间不可逆性总是存在的.

4 指数轻跳跃过程研究进展

作为高斯白噪声的推广, Lévy 噪声是另一种近年来备受关注的随机过程. 类似于高斯白噪声, Lévy 噪声可以看作是Lévy 过程的形式导数. 布朗运动是具有平稳独立增量性和概率1 连续样本路径的高斯过程, 而Lévy 过程去掉了高斯分布的要求, 并将概率1 连续退化至随机连续. 由此, Lévy 过程及Lévy 噪声驱动的随机微分方程的解一般是不连续的, 甚至跳跃点可能是稠密的(Duan 2015). 这一方面使得此类问题的处理变得相当困难, 但另一方面在研究地球气候的tipping现象 (Serdukova et al. 2017, Zheng et al. 2020)、基因转录过程中的突变 (Cheng et al. 2019, Chen X et al. 2019) 与股票市场的“笑状波幅 (implied volatility smile)” (Poirot & Tankov 2006) 等现象时, 人们发现Lévy 过程更加符合实际模型.

具体来说, 令Lt为Rn上的Lévy 运动, 定义跳跃过程ΔL(t)为

其中Lt-是Lt在t时刻的左极限.对于一个Borel 集S ∈B(Rn{0})和t>0,定义[0, t)时间区间内跳跃幅度落在S内的次数为

其中ω为样本路径.

定义一个在B(Rn{0})上的Borel 测度ν为

称为Poisson 随机测度, 或跳跃测度 (jump measure). 进一步, 定义补偿Poisson 随机测度为

则对任意t≥0,Lévy 运动Lt具有如下Lévy-Itô分解 (Duan 2015)

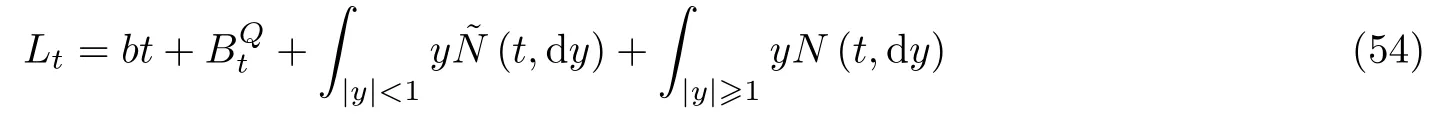
其中b ∈Rn,为 具有某个协方差矩阵Q的n维布朗运动. 数字1 将大跳跃与小跳跃分开, 实际上可以用任何正数替代. (b, Q, ν)称为Lévy 运动的生成三元组 (generating triplet).

根据Lévy-Khintchine 公式 (Duan 2015), Lévy 运动的特征函数为

其中I为示性函数. Lévy 运动的无限小生成元为

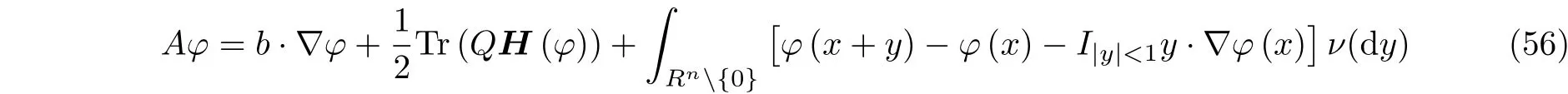
其中H为函数的Hessian 矩阵, Tr表示矩阵取迹. 实际上, 对于受Lévy 噪声激励的随机动力系统,式 (54) 中的前两项可以分别并入漂移与扩散项中. 因此, 人们通常考虑纯跳的Lévy 运动(0,0, ν).关于Lévy 运动及具有Lévy 噪声的随机微分方程的更多性质, 见文献 (Duan 2015, Applebaum 2009).

在满足某些假定下, Freidlin 和Wentzell (2012) 证明了Lévy 噪声和高斯白噪声驱动的随机微分方程满足大偏差理论, 并隐式的给出了其作用量泛函. 然而, 这些条件很难验证. 为此, Lipster和Puhalskii (1992) 利用随机微分方程的系数给出了这些假定的部分充分条件. Budhiraja 等(2011) 对具有Lévy 噪声的随机系统建立了Poisson 随机测度的泛函的变分公式, 并且推导了另一个满足大偏差原理的充分条件. 随后, 他们成功地将这一研究结果应用于满足合适条件的有限维 (Budhiraja et al. 2013) 和无限维 (Budhiraja & Fischer 2012) 随机动力系统的研究之中. 对于一维梯度系统, Imkeller 等 (2009) 研究了指数轻跳跃过程 (exponentially light jump process) 扰动的首次离出时间问题.

指数轻跳跃过程是一类特殊的Lévy 过程, 其跳跃测度满足ν(dy)=e-|y|αdy. 考虑随机动力系统

4.1 大偏差原理

为了简化, 考虑一维的情况. 当α≥1时, 随机系统 (57) 的解服从大偏差原理 (de Oliveira Gomes 2018, Yuan & Duan 2019)

其作用量泛函为

对任意的x,z ∈R, 定义拟势为 (de Oliveira Gomes 2018)

一般地, 若起始点z为系统的不动点, 则拟势简记为V(x).若D为包含不动点的待离出区域, 记和首次离出时间

则对任意的δ >0和x ∈D, 有 (de Oliveira Gomes 2018)

然而, 作用量泛函 (59) 的形式并不适合最优离出路径的计算. Yuan 和 Duan (2019) 给出了等价的另一种形式的作用量泛函

然而, 不同于高斯噪声的情况, 式中的拉格朗日量不能显式解析地表达. 幸运的是, 对应的哈密顿量, 即拉格朗日量的Legendre 变换, 具有下面的解析表达式

这里,p=∂L/∂x˙为动量. 积分项ypχ|y|≤1实际上为零, 因为测度ν关于y是对称的.

基于此, Li 等 (2020a) 推广了高斯情况下的计算最优路径和拟势的哈密顿形式 (Hamiltonian formalism) 应用于此类系统. 如前所述, 作用量泛函实际上支配着轨迹实现的可能性, 其全局最小值对应于概率最大的路径. 于是, 通过作用量泛函变分得到的辅助哈密顿系统的解提供了最优离出路径

于是, 这个哈密顿系统的积分解(x(t), p(t))到坐标空间的投影x(t)提供了最优离出路径.

从式 (64) 中注意到H(x,0)=0,则H(x1,0)=0 (x1为确定性系统的稳定不动点). 由于这样两个事实, 即最优路径连接不动点且哈密顿量在连续的相连轨道上为常数, 因此在整个最优路径上H(x,p)=0.注意到起始于x1的最优路径在x →x1时t0→-∞, 根据式 (60)、式(63) 及Legendre 变换, 可以得到, 在最优路径上

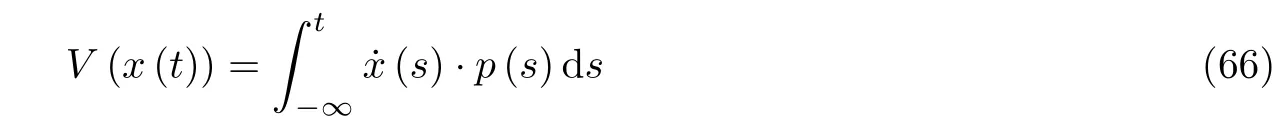
或等价地

注意, 方程 (65) 和 (67) 构成一组计算离出路径和拟势的完备微分-积分方程组. 然而, 仍然需要初始条件来进行数值积分. 从理论上讲, 当初始时间趋于负无穷时, 最优路径应该起始于不动点, 而在实际中这是不可能的. 于是, 初始点应选在扩展相空间的不动点的不稳定流形上, 并接近不动点. 因此, 需要在不动点附近进行局部线性化. 将B记为方程 (65) 的雅可比矩阵

可以看到B有两个特征值C ＜0,-C >0.对应于特征值-C的不动点的不稳定特征向量为(1,-2C/D)T. 因此, 最优路径的初始条件可以选为

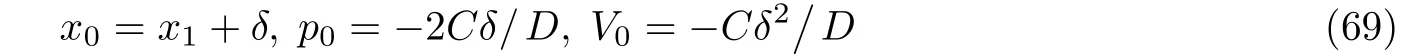
其中δ是一个小参数.

Li 等 (2020a) 给出了类似高维情况下具有指数轻跳跃噪声的随机动力系统的哈密顿形式, 以能量平衡模型和Maier-Stein 系统为例, 数值计算了系统的最优离出路径和拟势. 研究发现, 在一维情况下, 拟势的形状与势函数完全相同, 表明这种噪声定性类似于高斯噪声. 研究结果同时给出了拟势与跳跃测度的参数之间的解析近似关系, 并分析了跳跃测度对最优离出路径的影响. 在高维情况下, 发现了跳跃测度诱导的拉格朗日流形的奇异性.

4.2 中度偏差原理

中度偏差原理与大偏差原理的形式是类似的, 只是指数衰减率的阶数更低一些. 一般地, 中度偏差原理建立了随机过程xt穿过给定函数φt的小邻域的概率估计式

其中,S0T[φ]为作用量泛函,ε →0时,a(ε)→0且ε/a2(ε)→0,因此阶数ε/a2(ε)低于大偏差原理的ε.

由于理论上的难度, 目前关于中度偏差原理的研究还相对较少. Hu 和Shi (2004) 对一类具有“布朗势”的扩散过程建立了长时行为的中度偏差估计. Budhiraja 等 (2012, 2013) 对满足充分条件的有限维和无限维Lévy 型随机系统建立了中度偏差原理. 在此基础上, de Oliveira Gomes(2018) 证明了0＜α ＜1时的指数轻跳跃过程满足中度偏差原理, 并估计了平均离出时间的大小.

当0＜α ＜1时,可以证明方程 (57) 的解服从速率为εα的中度偏差原理, 即a(ε)=ε(1-α)/2, 其作用量泛函为

为此, 定义一个重整化偏差过程(renormalized deviation process)

可以证明, 此过程同样服从速率为εα的中度偏差原理 (de Oliveira Gomes 2018), 作用量泛函为

类似地, 定义拟势为

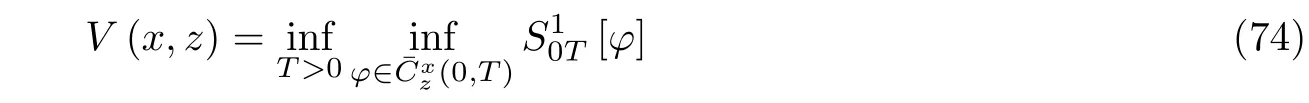
此时的拟势在有界区域内始终是有界的. 类似地, 若起始点z为系统的不动点, 则拟势简记为V(x).若D为 包含不动点的待离出区域, 记

给定y0=x ∈D, 考察离出时间

则对任意的δ >0和x ∈D, 有

根据过程yt的定义, 这个随机时间τε实际上是xt从区域+a(ε)D中的首次离出时间. 若考察未受扰系统的不动点, 即则中度偏差所关心的问题的本质实际上是系统从不动点的a(ε)阶小邻域中的离出现象.

5α 稳定Lévy 噪声研究进展

非高斯α稳定Lévy 噪声是最常见的一种Lévy 噪声, 具有广泛的实际应用, 其原因主要有两点. 一方面, 稳定随机变量X的定义为:X是一个尺度化序列(Sn-bn)/an的依分布极限, 其中SnX1+X2+···+Xn,{Xi}是一列独立同分布的随机变量序列,an >0,bn是某个实序列, 这里并不要求{Xi}具有有限的均值或方差 (Duan 2015). 也就是说, 稳定随机变量相当于高斯随机变量的推广, 其定义可以看成是广义的中心极限定理. 另一方面, 以旋转对称α稳定Lévy 运动为例,其跳跃测度为

其中的常数为

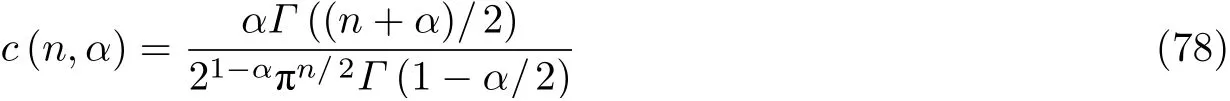
其中Gamma 函数Γ定义为. 无限小生成元为

其中, 右端项理解为柯西主值积分 (Cauchy principal value integral). 基于Fourier 变换发现, 这个积分算子本质上是一个分数阶拉普拉斯算子. 这两点使得α稳定Lévy 噪声不仅具有理论上的研究价值, 对实际物理系统也有重要的应用.

例如, 基于真实的格陵兰冰芯测量数据, Ditlevsen (1999) 发现气候变化系统可以建模为具有布朗运动和α稳定Lévy 过程的随机微分方程. 随后Zheng 等 (2020) 发展了一个概率框架来研究在温室效应和非高斯Lévy 噪声共同作用下的能量平衡系统的最大可能气候变化. 一些研究者发现在可激神经元模型中α稳定Lévy 噪声能够诱导随机共振现象 (Patel & Kosko 2008, Cognata et al. 2010). 此外, Liu 等 (2018) 研究了具有暂时免疫和Lévy 跳跃的延迟接种SIR 流行病模型的持久性和灭绝性. Guarcello 等 (2016) 通过将电流偏置的长约瑟夫森结建模为受振荡场驱动并受外部非高斯噪声影响的sine-Gordon 方程, 对其动力学进行了数值研究. 理论上, 具有布朗运动和Lévy 过程的随机微分方程可以用来模型化一大类重要的马氏过程, 称为Feller 过程 (Böttcher 2010).

这些工作表明, 具有α稳定Lévy 噪声的随机动力系统是具有深刻科学意义的现象学模型. 本节针对此类系统, 介绍离出现象及其相关动力学行为的主要处理方法和近期研究进展.

5.1 平均首次离出时间和离出概率

考虑一维随机动力系统

其中Bt为布朗运动,为对称α稳 定Lévy 过程, 跳跃测度满足να(dy)=c(1,α)|y|-1-αdy,Λ和σ分别是对应的噪声强度. 则系统的生成元为

引言中方程 (1) 和 (2) 分别给出了高斯白噪声条件下平均首次离出时间和离出位置分布满足的狄利克雷边值问题. 根据Dynkin 公式, 针对形如式 (80) 的系统, 平均离出时间v(x)仍满足类似的方程 (Duan 2015)

只是其中的算子改为生成元 (81), 边界条件由D的 边界上的值改成D的补集Dc上的值.

另一方面, 由于Lévy 过程的跳跃特性, 离出位置分布的概念已不再适用, 因为系统离出时未必与边界相交. 取而代之的是离出概率 (escape probability) 的概念, 即系统起始于区域D中的x,首次离出区域D时落在Dc的某个子集E内的概率, 记为PE(x), 满足下面的方程 (Duan 2015)

根据生成元的形式 (81), 可以发现方程 (82) 和 (83) 是微分-积分方程, 并且积分算子是奇异积分, 因此求解的难度远大于仅有高斯噪声的情况. 由于复杂性较高, 目前处理此类问题的解析方法较少, 只有在特殊情况下能近似求解. 例如Λ=0,σ为小量, 即无高斯噪声且Lévy 噪声较弱,此时基于α稳定Lévy 噪声尾部的多项式衰减特性, 可利用多项式级数摄动近似平均离出时间和离出概率 (Qiao & Duan 2015).

然而, 多数情况下, 得到这两个方程的理论解是较为困难的, 为此发展相应的数值方法是十分必要的. 通过将积分分割为并数值离散化, 且利用差分代替微分,Gao 等 (2014) 设计了一个有效的数值方法用来计算平均离出时间和离出概率. 基于此方法, Wu等 (2018) 计算了一个基因表达模型的平均离出时间、离出概率和随机吸引域 (stochastic basins of attraction), 采用非高斯与高斯噪声强度之比来识别转移过程中的最优选择. Cai 等 (2017) 通过计算离出时间与离出概率来刻画神经元系统中α稳定Lévy 噪声诱导的兴奋事件. Xu 等 (2016)通过计算稳态概率密度和平均离出时间, 研究了非高斯噪声对相干转换和开/关转换的影响. 反过来, 基于对平均离出时间的观测, Zhang 等 (2020) 设计了一个数据驱动方法, 能够从离出时间数据中提取具有高斯布朗噪声或非高斯Lévy 噪声的随机微分方程.

5.2 Onsager-Machlup 理论

为了从理论上确定最优离出路径, 本节引入Onsager-Machlup (OM) 理论. OM 理论是研究随机动力系统离出现象的常用方法, 其基本思想是利用围绕某条路径的固定厚度的管道的概率来代替这条路径实现的可能性, 可以看成是Freidlin-Wentzell 大偏差理论在有限噪声强度下的推广. 在高斯噪声情况下, OM 作用量泛函比Freidlin-Wentzell 作用量泛函多了一项漂移系数的散度项, 在弱噪声极限下OM 作用量泛函退化为Freidlin-Wentzell 作用量泛函的结果.

早在1953 年, Onsager 和Machlup (1953) 首先导出了具有线性漂移系数和常扩散系数的扩散过程的OM 泛函. Tisza 和Manning (1957) 随后对非线性系统进行了扩展. 此外, Dürr 和Bach(1978) 提出了另一种推导OM 泛函的方法, 将Girsanov 变换应用于扩散过程诱导的测度. Chao和Duan (2019) 将此方法推广到求解 (非高斯) Lévy 噪声和 (高斯) 布朗噪声下随机动力系统的更复杂情况. Tang 等 (2014, 2017) 从另一个方面进一步推导了带乘性高斯噪声的过阻尼朗之万方程和一般随机解释的OM 泛函. 综合以上研究成果, 本节介绍较为一般的乘性高斯噪声和加性非高斯Lévy 噪声驱动下的随机动力系统的OM 理论.

考虑下面的n维随机动力系统

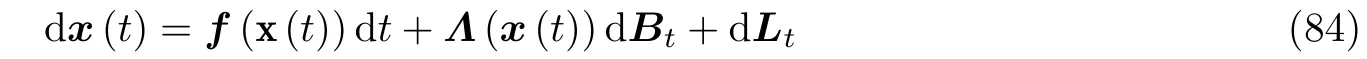
其中Bt=[B1,t, B2,t ··· , Bn,t]T是n维布朗运动,Lt=[L1,t, L2,t ··· , Ln,t]T是非高斯Lévy 过程, 其跳跃测度ν满足. Lévy 过程的大幅值跳跃可以通过交错 (interlacing) (Applebaum 2009) 方法来处理, 因此这里只考虑小跳跃是第4 节引入的补偿Poisson 随机测度. 向量f(x)=[f1(x), f2(x), ··· , fn(x)]T为漂移系数,ΛΛT是扩散矩阵.

对于具有乘性高斯噪声的方程 (84), 选择积分方法时的模糊性会导致不同的随机解释, 一般表示法为α-解释 (Shi et al. 2012). 为了避免与α稳定Lévy 噪声的参数混淆, 采用κ解释代替α.κ=0,κ=1/2和κ=1分别对应于Itô, Stratonovich 和anti- Itô的解释. 通过修正漂移项, 随机微分方程 (84) 可以转化为统一的Stratonovich 形式

其中

记为修正的漂移系数. 使用这种统一的Stratonovich 形式的优点是可以简单地应用普通的微积分法则, 由此为路径积分法推导后续的OM 函数 (Tang et al. 2014) 带来了一些便利. 事实上,统一随机解释形式的选择只影响推导过程, 而不影响OM 函数的结果.

在随机扰动下, 亚稳态之间可能发生跃迁. 在这个过程中, 最感兴趣的是确定最大可能的转移路径. 由于单条路径的概率必然为零, 需要研究随机轨迹通过某条路径的邻域或管道的概率.在给定管道厚度的条件下, 轨道留在管内的概率实际上描述了这一特定路径实现的可能性. 更准确地说, 考虑一个围绕参考路径φ(t),t ∈[0, T]的管道. 如果δ足够小, 则解过程x(t)落在管道内的概率可按以下形式估算

因此, 类似于Freidlin-Wentzell 大偏差理论的结果, OM 泛函的全局最小值对应于具有最大概率的路径, 即最优路径. 于是, 概率的计算转化为OM 泛函的变分问题. 基于分析力学的经典结果, 连接点x0和点xf的最优路径满足欧拉-拉格朗日方程

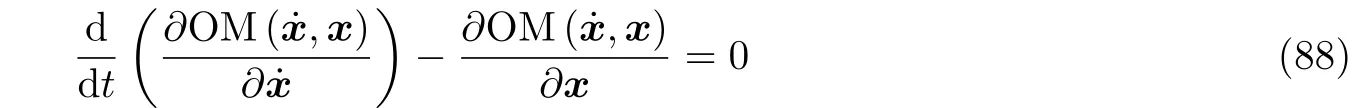
其边界条件为x(0)=x0和x(T)=xf. 这里将符号φ替换为了x. 因为这是一个二阶微分方程, 将它转化为一个等价的哈密顿系统对于数值积分会更为方便

这里,H(x,p)是OM 函数的Legendre 变换,p=OM(x˙,x)/x˙为动量. 解(x(t),p(t))到坐标空间的投影x(t)给出了最优路径.

根据文献 (Chao & Duan 2019, Tang et al. 2014), 方程 (87) 的OM 函数在不考虑加性常数的情况下由下式给出

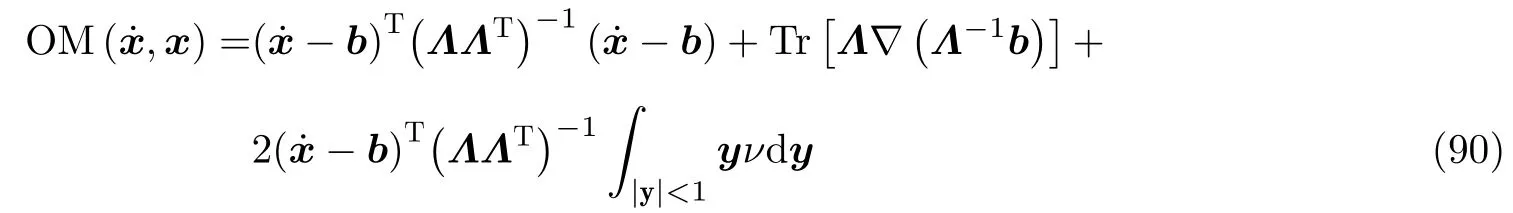
其中Tr[A]=. 为了方便, 记yνdy. 则Legendre 变换计算出的哈密顿量为

因此, 哈密顿系统具有下面的形式

若高斯噪声为加性的, 方程约化为

对式 (90) 中OM 函数的形式作两点说明. 一方面, 如果考虑α稳定的Lévy 运动, 则条件＜∞要求0＜α ＜1.另一方面, 当令式 (90) 中的ν=0时, 它恢复为扩散过程的OM函数. 换句话说, Lévy 噪声对跃迁现象的影响反映在式 (90) 中OM 函数的第三项中. 特别地, 如果Lévy 运动是对称的, 则结果与扩散过程的结果是一致的.

5.3 计算最大可能路径的机器学习方法

注意5.2 节中的方程 (93) 是一个常微分方程的两点边值问题, 通常可以用shooting 方法来处理. 也就是说, 可以调整动量的初始值并对方程进行数值积分, 直到终点x(T)抵达xf. 然而, 这种方法在实践中仍存在两个不足之处. 第一, 通常选择一个称为亚稳态的稳定不动点作为初始点x0来考虑它的跃迁. 由于共轭动量方程 (即式 (93) 中的第二个方程) 包含-(∇f)Tp, 因此在时间上向前的数值积分在数值上是不稳定的, 甚至是不适定的. 此外, 在高维系统中会出现另一个问题,即很难决定应该调整初始动量的哪一分量. Li 等 (2021) 设计了一个机器学习方法来解决这两个问题, 算法分为哈密顿系统的重公式化和神经网络算法两部分.

首先, 为了处理动量的发散问题, 记ST[x(t)]=dt并且

其中C1={x ∈C[0,T]|x(0)=x0, x(T)=xf}. 另外, 定义

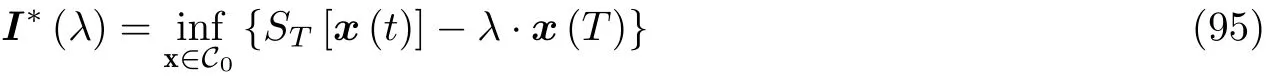
其中C0={x ∈C[0,T]|x(0)=x0}. 注意这个极小化并不在终点上施加约束. 换句话说, 函数空间C0刻画了起始于 x0无所谓终点的连续轨道的集合. 事实上,I∗(λ)和I(xf)构成一组Fenchel-Legendre 变换对.

I∗(λ)和I(xf)的关系事实上允许处理最小化问题 (95) 来代替 (94). 式(95) 的变分结果导出下面的哈密顿系统

从式 (89) 可以看出, 边界条件约束在初始坐标和最终坐标上, 但在动量上不存在. 而在式(96) 中, 它们被转换成一个坐标的边界条件和另一个动量的边界条件. 这种操作的好处是显而易见的. 式 (96) 的计算是时间前向积分x(t),然后时间后向积分动量p(t). 这种方法成功地解决了前面提到的shooting 方法的第一个缺点, 因为两个方向的积分都是收敛的.

这个方法的算法总结如下:

算法1:

Step 1 给定λ的一个值和一条初始轨迹xk(t)(初始k=1);

Step 2 从p(T)=λ时间后向积分方程(xk,p)得到pk;

Step 3 从x(0)=x0时间前向积分方程(x,pk)得到xk+1;

Step 4 迭代Step 2 和Step 3 直到收敛.

接下来, 如何根据x的 终点边界条件确定λ的值可以通过一个深度神经网络来完成, 该神经网络的结构如图5 所示. 根据研究目的, 输入和输出状态分别固定为xf和λ,每个状态都有n个分量.假设在输入和输出之间有L层隐藏层, 第l层有nl个神经元,l=1,2, ··· , L. 因此, 一个复杂的非线性函数可以用一系列简单函数的复合来近似

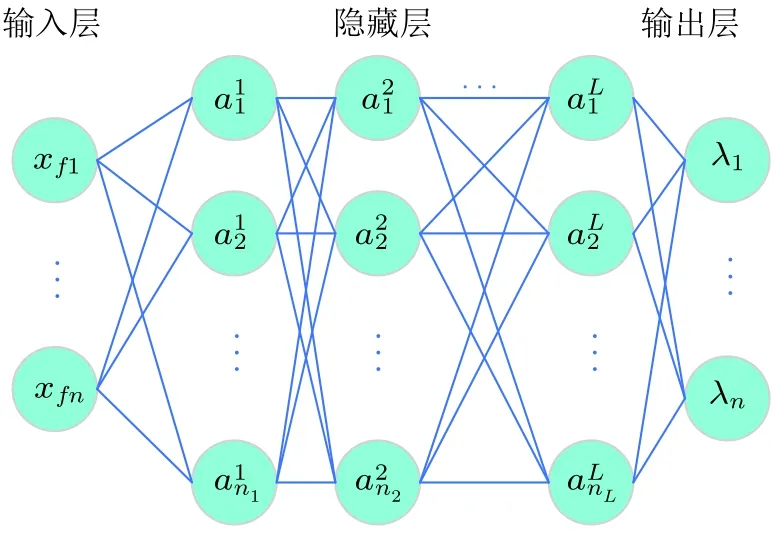
图 5具有 L层隐藏层的神经网络的结构. xfi和λi,i=1, 2, ··· , n分别是神经网络的输入和输出.表示第 l层第 j个神经元的值,其中j =1, 2, ··· , nl,l=1, 2, ··· , L

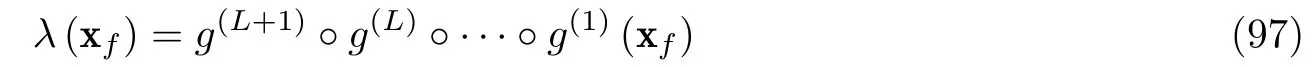
每层的函数g(l)(·)定义为

为方便起见, 记a(0)=xf和a(L+1)=λ.此外,W(l)和b(l)分别称为权重矩阵和偏置向量.σ(l)表示一个非线性激活函数, 应用于变量的每个分量上, 常用的函数有sigmoid, tanh, ReLu 等. 接下来, 对所有隐藏层使用ReLu 函数ReLu(x)=max{0,x}.而输出层选择恒同函数, 以覆盖λ的空间.

令θ为这个神经网络参数的集合, 即θ={W(l), b(l):l=1,2, ··· , L+1}. 神经网络的训练是通过对参数θ进行优化, 使其输出状态能够最优地逼近λ(xf).具体来说,假设有数据集D=, 并引入网络预测和目标之间的L2距离作为损失函数(loss function). 然后通过搜索最优参数对神经网络进行训练, 求解损失函数的非线性回归问题

λNN表示输入数据时网络的输出. 一般地, 最小化参数通过梯度下降法进行迭代

其中学习率 (learning rate)η是一个较小的数.

神经网络的训练过程总结如下:

算法2:

Step 1 给定数据集和初始参数集θ0;

Step 2 应用前向传播计算网络的输出和代价函数;

Step 3 应用后向传播计算代价函数对参数的梯度;

Step 4 利用方程 (100) 迭代参数;

Step 5 迭代直到收敛.

作为总结, 算法框架如下:

算法3:

Step 1 生成数据: 具体来说, 在λ的空间的一个合适的区域随机选择M个点. 将初始点固定在系统的稳态, 利用算法1, 对λ的每个点计算最大可能路径x(t);

Step 2 训练神经网络: 基于算法2, Step 1 生成的数据可用于训练神经网络, 其中x(T)为输入,λ为输出;

Step 3 测试: 给定某个终点xtest,利用训练好的神经网络来计算对应的输出λtest;

Step 4 计算最大可能路径: 再次利用算法1 对λtest计算最大可能路径, 将终点与xtest做对比.

此机器学习方法在两个典型例子中的成功应用(Li et al. 2021a), 证实了它对于有或没有Lévy 噪声、加性或弱乘性高斯噪声、不同随机积分解释 (Itô意义、Stratonovich 意义和anti-Itô意义) 的系统以及各种维数的系统的有效性. 结果表明, 该方法相比非高斯噪声更适用于高斯噪声, 相比乘性噪声更适用于加性噪声, 该算法对Stratonovich 意义是最有效的, 然后anti- Itô的,再之后Itô的.

这种方法还可以推广到其他类似的问题. 例如, 除了OM 理论外, 在计算Freidlin-Wentzell 的大偏差理论下的最大可能路径时仍然可行. 更广泛地说, 它也可以应用于其他领域, 如最优控制问题等.

最后, 值得注意的是, 该算法在实际应用中还存在一个挑战. 如果积分结果的数据xf分布相对均匀, 则可以更有效、更准确地训练神经网络. 然而, 如果这些点集中在几个特定的区域中, 由于损失函数在各个区域的权重差异过大, 则效果不佳. 因此, 该算法的成功应用要求系统的向量场具有某种均匀性.

5.4 计算最大可能路径的最大似然法

尽管具有Lévy 噪声的随机动力系统的OM 作用量泛函已有结果, 然而它只对某一类Lévy噪声成立, 应用具有局限性. 另一方面, 理论结果也需得到数值方法的验证. 因此, 发展其他的计算最大可能路径的方法是十分必要的. 基于转移概率密度满足的Fokker-Planck 方程, Zheng 等(2020) 开发了一种计算最大可能路径的最大似然法.

为了方便表示, 以一维系统为例

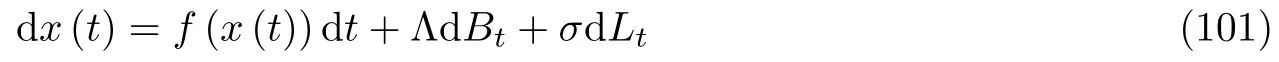
p(x(t)=u)代表随机微分方程 (101) 的解位于x(t)=u的概率密度, p(u,t|z,s)表示给定x(s)=z的条件下到x(t)=u的转移概率密度, 其中0 ≤s ＜t≤tf, 即

根据 (Duan 2015), 转移概率密度p(u,t|z,s)满足下面的Fokker-Planck 方程

右边的积分部分实际上是非局部或分数阶拉普拉斯算子, 对应非高斯α稳定Lévy 扰动. 转移概率密度的初始条件满足

对任意的t ∈[0,tf],x, x0, xf ∈Rn,假设条件概率密度PA(x,t)用于刻画在条件A下x(t)在时刻t位于点x的概率密度. 这里, 条件A指初始条件x(0)=x0和终止条件x(tf)=xf. 根据马氏性, 它可以表示为

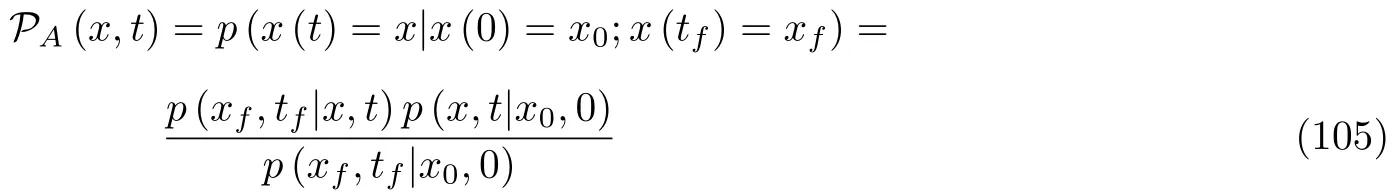
在条件A下, 对任一时刻t ∈[0,tf],密度函数PA(x,t)出现的峰值位置对应状态xm(t). 这意味着, 在给定时刻t, 条件概率密度PA(x,t)的峰值位置xm(t)记为这些随机轨道的最大可能位置, 即

将所有这些位置连接起来即得到从初始位置x(0)=x0转移到终点位置x(tf)=xf的最大可能轨迹.

式 (105) 中的转移概率密度p是 Fokker-Planck 方程 (103) 的解, 理论求解相当困难. 为此, 基于时间-空间离散化的Toeplitz 矩阵结构, Gao 等 (2016) 提出了一种快速精确的数值算法用于计算具有吸收边界或无穷区域的非局部Fokker-Planck 方程, 并证明了其收敛性. 目前, 这个方法已经广泛应用于离出现象 (Chen X 2019)、随机分岔 (Wang 2020) 和数据驱动方法 (Zhang 2017) 等相关问题中. 另外, 机器学习方法也可以应用于求解Fokker-Planck 方程, 例如Xu 等 (2020) 利用深度神经网络计算高斯噪声下的概率密度, Chen 等 (2020) 基于样本路径数据求解同时具有高斯布朗噪声和非高斯Lévy 噪声的随机系统Fokker-Planck 方程.

5.5 非局部Kramers-Moyal 公式

对于实际工程结构和自然科学等问题的研究, 人们通常利用牛顿第二定律或拉格朗日力学等理论建立系统的动力学方程. 通过求解此控制方程, 希望得到系统的响应, 或得到系统的一些动力学性质, 例如计算不同稳态的转移路径. 然而, 由于人们对许多复杂现象的内部机制缺乏完备的理解, 如生物医药、脑科学、大气科学等领域, 很难直接建立其显式的运动方程. 幸运的是,随着科研工具和仿真能力的进步, 人们能够获得越来越多的复杂系统数据集. 因此, 从噪声数据中提取控制规律或动力学特性在各个科学领域都起着至关重要的作用.

针对具有高斯布朗噪声的随机动力系统, Dai 等 (2020) 提出了一个数据驱动框架, 用以从样本数据中提取最大可能转移路径. 此方法的基本思想是, 先利用Kramers-Moyal 公式从样本路径数据中提取随机微分方程的漂移和扩散系数, 然后利用前一子节的最大似然法计算最大可能路径. 然而, 这种方法无法直接推广到具有非高斯Lévy 噪声的情况. 其原因在于,α稳定分布的尾部多项式衰减, 具有重尾 (heavy-tailed) 特性, 其二阶矩及以上必然发散, 一阶矩是否发散依赖于α的取值. 因此, Kramers-Moyal 公式不再适用Lévy 噪声的情况. 另一个难点在于此时的Fokker-Planck 方程是微分-积分方程, 这也使得问题变得更加复杂. 幸运地是, Li 和Duan (2021) 推导的非局部 (nonlocal) Kramers-Moyal 公式有效解决了这个问题, 下面对此公式做简要介绍.

考虑一个n维 随机动力系统

其中b(x)=[b1(x), b2(x), ··· , bn(x)]T是 Rn中的漂移系数,Bt=[B1,t, B2,t, ··· , Bn,t]T是n维布朗运动,Λ(x)是一个n×n的矩阵,Lt=[L1,t, L2,t, ··· , Ln,t]T是具有正常数噪声强度σ的对称Lévy运动. 假定初始条件为x(0)=z,a(x)=ΛΛT为扩散矩阵,Lt的跳跃测度满足ν(dy)=W(y)dy,y ∈Rn{0}.由于Lévy 运动的对称性,W(-y)=W(y).

基于系统 (107) 的Fokker-Planck 方程, 可以推导出下面的定理和推论.

定理1对每个ε>0,概率密度函数p(x,t|z,0)和跳跃测度、漂移、扩散具有如下的关系:

(1) 对每个满足|x-z|>ε的x和z

对x和z一致成立;

(2) 对i=1,2, ··· , n

(3) 对i,j=1,2, ··· , n

这个定理的思想可以按照下述方式理解. 在不含Lévy 噪声的情况下, Itô随机微分方程的样本轨道是概率1 连续的. 也就是说, 漂移系数和扩散系数贡献的是连续部分, 而Lévy 噪声贡献的是跳跃部分. 在很短的一段时间内, 大的跳跃几乎都来自于Lévy 噪声. 依据这个思想, 这个定理将相空间分割为球内和球外两部分. 球外部分 (即定理的第一条) 用来表达Lévy 跳跃项, 球内部分 (即定理的第二条和第三条) 用来表达漂移和扩散项. 由于将积分区域限制在球内, 从而有效避开了重尾特性导致积分发散的问题, 成功地将漂移、扩散与Lévy 跳跃项利用转移概率密度来表达. 然而, 这个定理对于数值算法的设计并不友好. 为此, 可以将其改写成下面的推论形式, 从而将漂移、扩散与Lévy 跳跃项利用样本路径数据来表达:

推论1对每个ε>0, 随机微分方程 (107) 的解和跳跃测度、漂移、扩散具有如下的关系:

(1) 对每个m>1

这个推论第二条和第三条与Kramers-Moyal 公式具有类似的形式, 因此这个推论可以称为非局部Kramers-Moyal 公式. 对于推论的第一条, 考虑多个不同的区间, 可以近似得到Lévy 跳跃测度和噪声强度. 关于第二条和第三条, 利用基函数的线性组合近似, 并结合最小二乘法, 可以估计出漂移与扩散项的近似表达式. 具体的数据驱动算法的设计参考文献 (Li & Duan 2021), 这里不再详细介绍. 因此, 给定样本路径数据, 利用非局部Kramers-Moyal 公式, 可以识别出具有高斯布朗噪声和非高斯Lévy 噪声的随机动力系统, 结合上一节介绍的最大似然法, 可以计算出系统亚稳态间转移的最大可能路径, 从而从样本路径数据中提取出了最大可能路径.

最后, 可以发现, 将这种方法扩展到具有乘性Lévy 噪声的随机动力系统的数据集是一个挑战. 在这种情况下, 乘性Lévy 噪声破坏了定理1 中第一个断言的“空间齐次性”, 导致函数W同时依赖于x和z(而不仅仅依赖于空间平移x-z), 从而给数据驱动算法的设计带来了困难 (Li &Duan 2021).

6 展 望

严格意义上, 在自然科学、社会科学和工程科学等领域中, 非高斯模型比高斯过程更具有普遍性, 但同时非线性非高斯噪声系统的随机动力学行为亦更为复杂. 随着人们对自然现象的描述越发精细, 新的问题层出不穷, 对大偏差理论在非高斯随机动力系统的应用提出了更多的挑战.以发展的眼光来看, 从以下几个方面提出一些潜在性问题:

(1) 如前所述, 用于计算随机混合系统的离出问题的哈密顿量是一个符号矩阵的主特征值.然而, 对于高维的问题, 目前只有个别特殊系统能够解析求解. 对于一般的随机混合系统, 如何解析近似或数值计算其哈密顿量仍是一个巨大的挑战;

(2) 近年来随着计算机技术的蓬勃发展, 机器学习方法以其强大的功能被广泛应用于解决动力系统中的难题, 如利用机器学习方法求解哈密顿-雅可比方程、Fokker-Planck 方程和变分问题等. 由于计算大偏差问题中的最大可能路径和拟势的难度较大, 在大量观测和模拟数据的基础上, 利用机器学习方法来求解大偏差问题具有广阔的应用前景.

致 谢国家自然科学基金资助项目 (11772149).