粗糙表面微型气体轴承润滑性能及其转子动力学特性研究
吴 垚, 杨利花, 郗文君, 张彩丽, 毕春晓, 王 哲, 曹巨江
(1.陕西科技大学 机电工程学院, 陕西 西安 710021; 2.西安交通大学 机械结构强度与振动国家重点实验室, 陕西 西安 710049; 3.施耐德(西安)创新技术有限公司 低压事业部, 陕西 西安 710075; 4.中国科学院 工程热物理研究所, 北京 100190; 5.西安工程大学 材料工程学院, 陕西 西安 710048)
0 引言
微型气体动压轴承具有高Knudsen数,长径比小、隙径比大等特点,相比滚动轴承在高速运转时产生噪声、抗冲击性能差、很难承受高温环境,磁悬浮轴承易受到外界电磁干扰以及静压气体轴承需要附加供气系统导致装置结构复杂、造价较高等方面的不足,微型气体轴承可作为微型燃气轮机、微型涡轮发动机、小型无人机超高速涡喷发动机和微型涡轮增压器等微型旋转机械中微型转子最佳的支承型式[1].微型气体轴承-转子系统作为微型旋转机械的关键单元,支承旋转设备的各种负荷和振动激励通过转轴传到轴承上,其润滑性能和转子系统设计对设备结构完整性、安全平稳工作具有重要的理论指导意义.
随着轴颈/轴瓦间润滑气膜厚度不断减小,微纳尺度下稀薄气体流动问题与宏观尺度下的流动特性显著不同[2],微型动压气体滑动轴承和轴颈之间的载荷是由超薄气膜和轴瓦表面微观形貌的直接挤压共同承担,当微型气体滑动轴承最小气膜厚度降低到接近表面粗糙度量级,气体稀薄效应和表面粗糙度的耦合影响不可忽略.
早在1959年Burgdorfer[3]首次将分子动理论引入气体润滑领域,提出了考虑一阶速度滑移边界条件的修正雷诺(Reynolds)方程.随后,Hsia[4]、Mitsuya[5]、Fukui[6,7]、Bahukudumbi和Beskok[8]、Wu[9]等分别提出了不同的稀薄效应模型,为微型动力旋转机械尤其是微机电系统(MEMS,Micro-Electro-Mechanical System)的快速发展提供了基础理论.1967年,Tzeng等[10]利用随机β分布表征了滑动轴承表面形貌,研究了表面粗糙度对滑动轴承压力形成、承载力和摩擦力的影响.随后Christensen和Tonder[11]将轴承的润滑膜厚分为名义膜厚和可变粗糙度膜厚两部分,阐明了表面粗糙度、结构尺寸和运行参数对轴承润滑性能的耦合作用机理.1978年,Patir和Cheng[12]基于经验压力和剪切流因子,提出了用流量因子、平均压力和名义膜厚等平均量来表示的平均Reynolds方程.黄平和牛荣军等[13]利用余弦粗糙度模拟真实磁盘表面粗糙形貌,给出了纳米气膜承载能力和最大压力随粗糙度波长和磁盘飞高的变化趋势.White[14]推导并求解了适于大Knudsen数气流和不同条纹粗糙表面的润滑方程,该方法显著降低了数值求解的计算时间和网格要求.Zhang等[15]通过分形几何表征粗糙轴承表面,建立了滑移流区和过渡流区域中考虑速度滑移边界条件的修正Reynolds方程,详细讨论了不同轴承数、Knudsen数、轴承结构以及粗糙度参数下气体轴承复杂的流动行为.Wang等[16]利用线性扰动法迭代求解了气体静压滑动轴承非稳态Reynolds方程,得到了不同运行参数和轴瓦表面波纹度下动态刚度和阻尼系数的变化曲线,结果表明动态系数的绝对值随波纹度幅值增加而显著上升.
关于气体轴承-转子系统动力学特性的研究,Wang[17]耦合微分变换法和有限差分法研究了球面气体润滑轴承支承的柔性转子系统的动力学行为,揭示了转子中心和轴颈中心周期响应、亚谐波响应以及准周期响应的复杂动力学行为.张翰乾[18]基于线性摄动法得到的高速静压气体轴承动态特性,建立了固定和柔性安装两种条件下静压气体轴承-转子系统的动力学模型,采用Newmark法、Routh-Hurwitz判据以及转子动力学实验分别对转子系统的稳定性和不平衡响应进行了分析.刘健[19]针对垂直供气气体轴承-转子系统的结构特点,分别利用QR分解法和Newmark逐步积分法计算了气体轴承-转子系统的临界转速、振型和不平衡响应,说明了转子系统的前两阶平动或锥动临界转速较为接近,三阶临界转速为弯曲振动,工作转速应选择在二、三阶临界转速之间.Yang等[20,21]根据微型转子的运动方程,采用四阶Runge-Kutta法计算了微型气体轴承-转子系统的不平衡响应,研究表明合适的转子偏心质量可以提高转子系统的稳定性,考虑气体稀薄效应的微转子系统的稳定阈值速度有所提高.Li等[22]通过构建气体轴承-转子系统的瞬态模型,研究了比力突然变化对气浮支承陀螺仪性能的影响,结果表明比力的突变方向是改变干扰力矩曲线的主要因素.
综上所述,目前有关微型气体轴承薄膜润滑的文献多集中于静态性能,气体稀薄效应和表面粗糙形貌对轴承动态系数和转子系统动力学特性耦合影响的研究较少.本文利用Weierstrass-Mandelbrot(W-M)函数表征轴瓦表面三维粗糙形貌,采用偏导数法和松弛迭代法求解粗糙微型气体轴承超薄气膜润滑修正Reynolds方程,讨论了分形维数对微型轴承承载能力、摩擦系数和动态系数的影响规律,并采用Timoshenko梁理论得到微型气体轴承-转子系统的运动方程,分析了考虑微型气体轴承动态系数的频率效应、气体稀薄效应和表面粗糙度对转子系统固有特性和轴心轨迹的影响.
1 粗糙表面的分形模拟
由于粗糙表面随机性强、形成过程较为复杂且在空间上具有离散性,借助计算机对表面粗糙度进行仿真模拟和分析是虚拟摩擦学的重要技术基础.大部分机械加工表面都具有分形特性,利用Weierstrass-Mandelbrot(W-M)分形函数[23]构造三维粗糙表面轮廓为
(1)
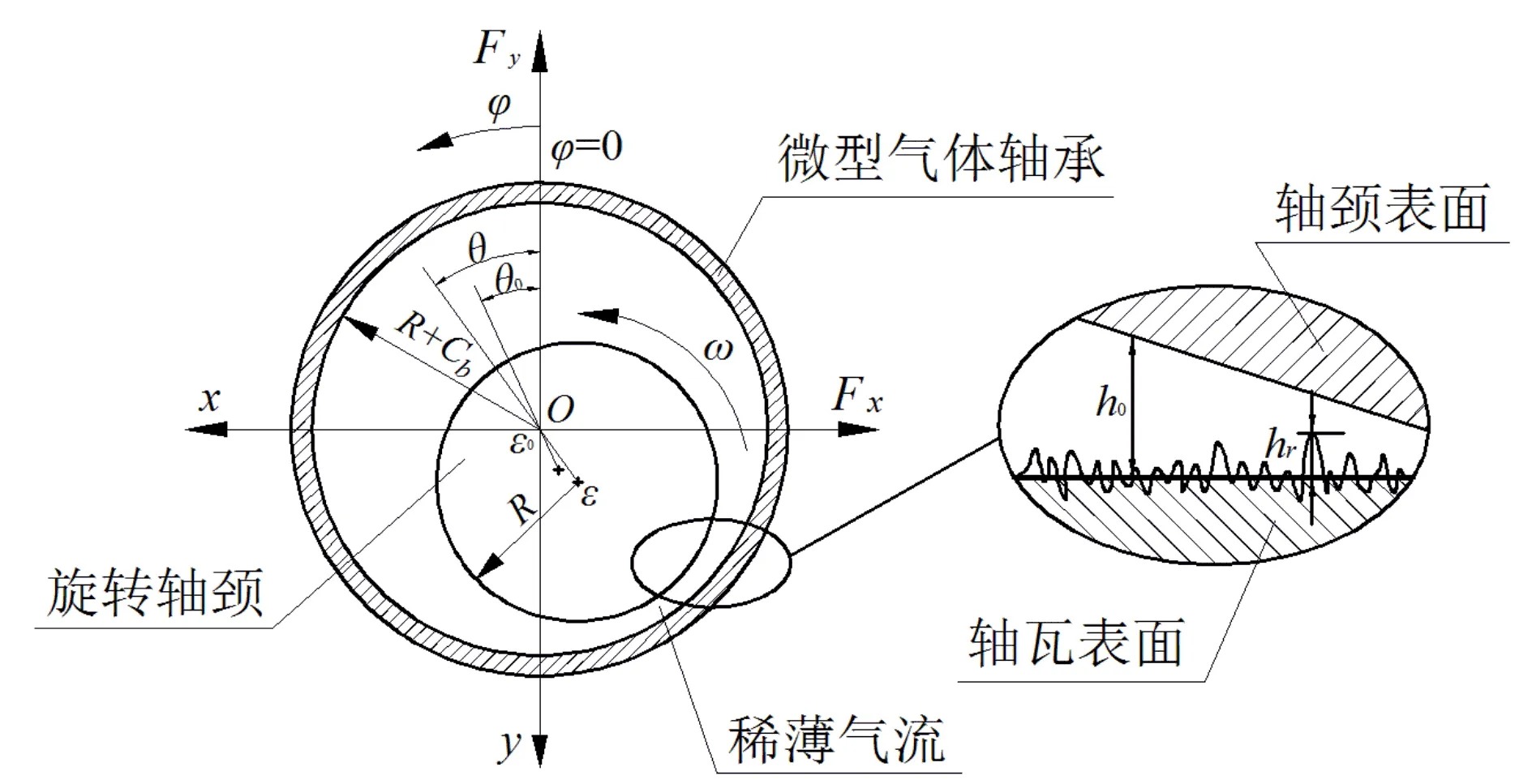
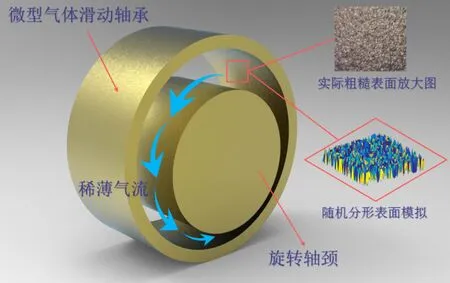
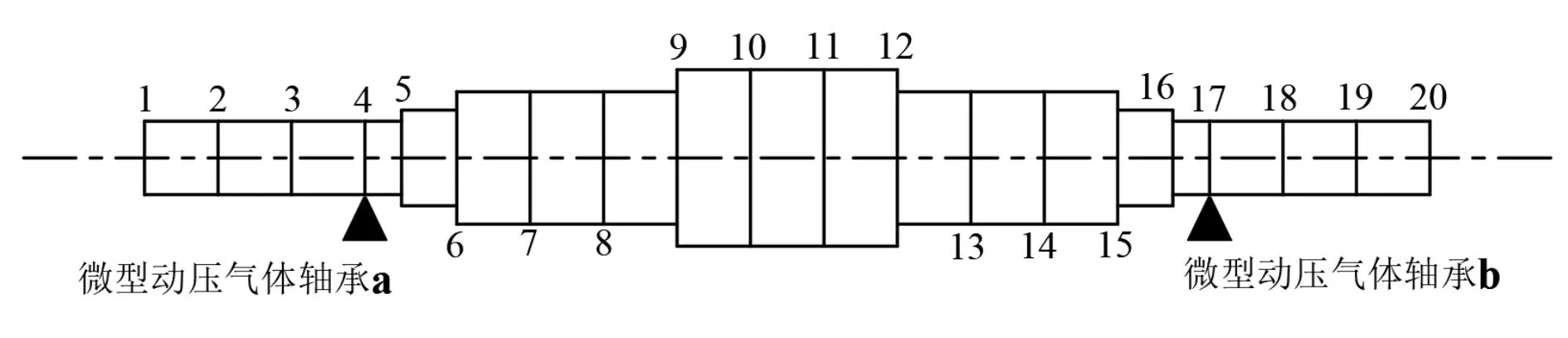
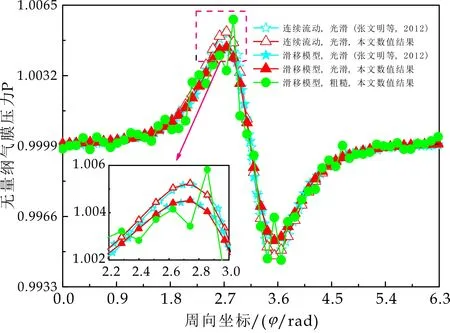
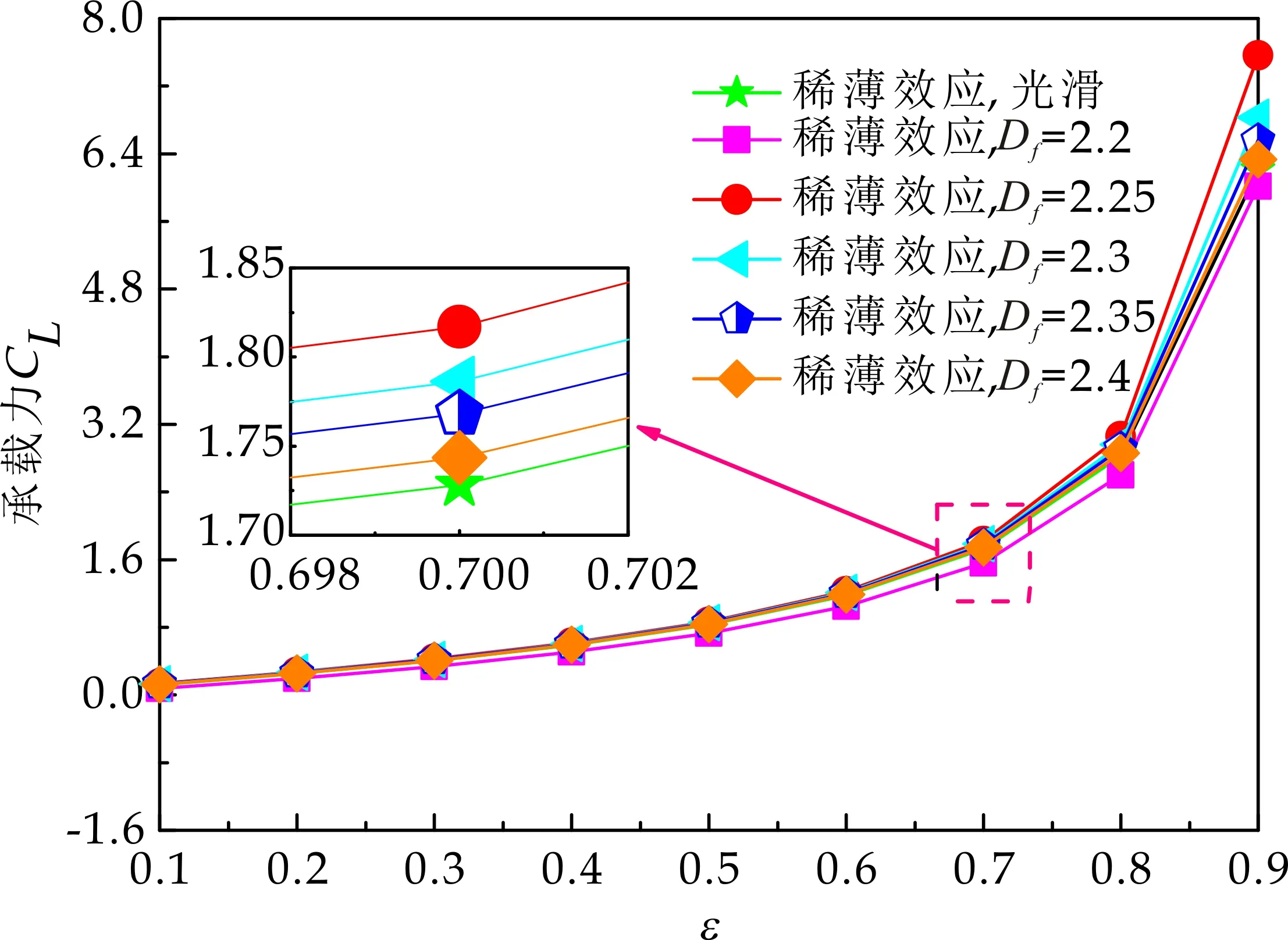
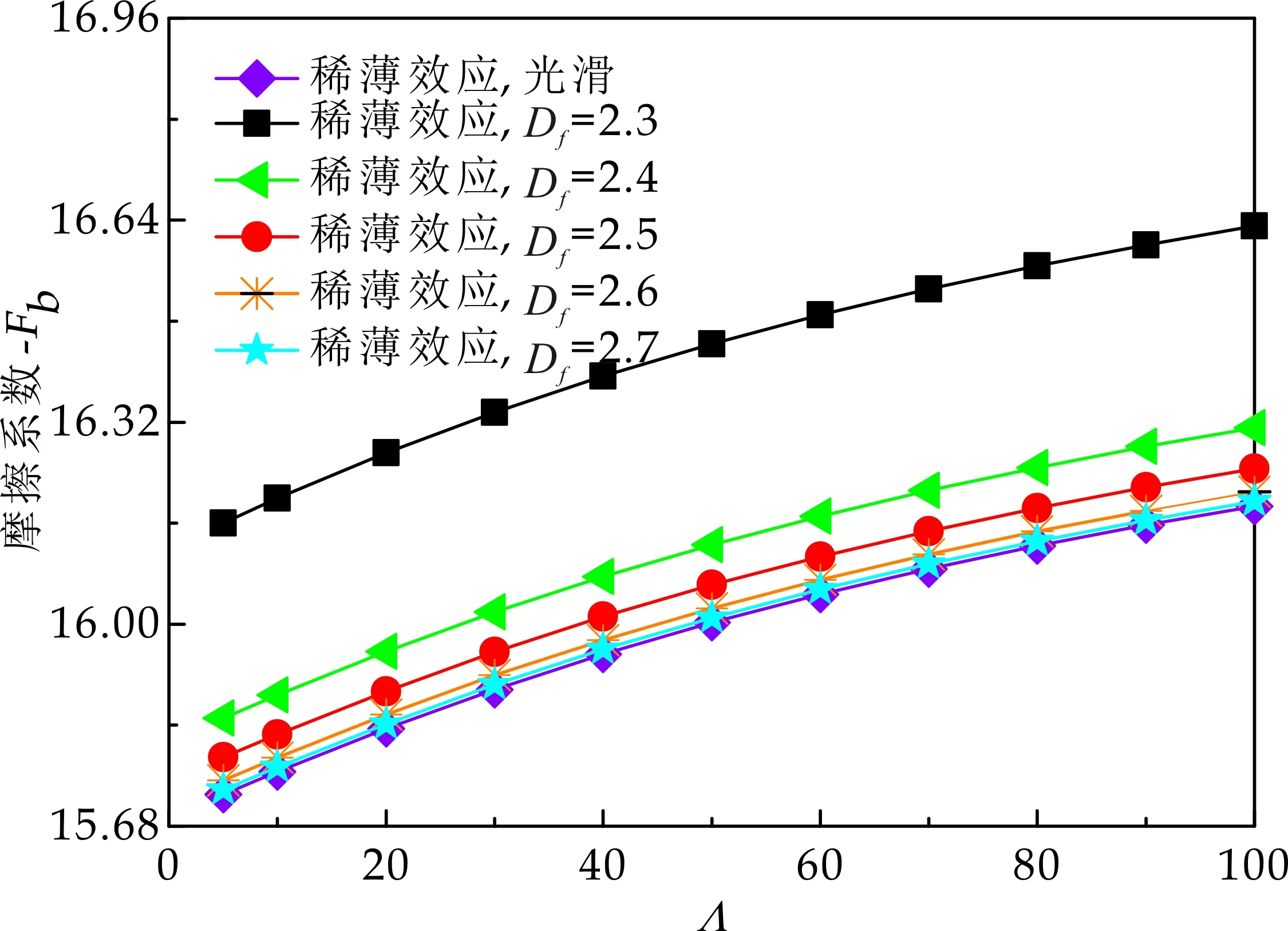
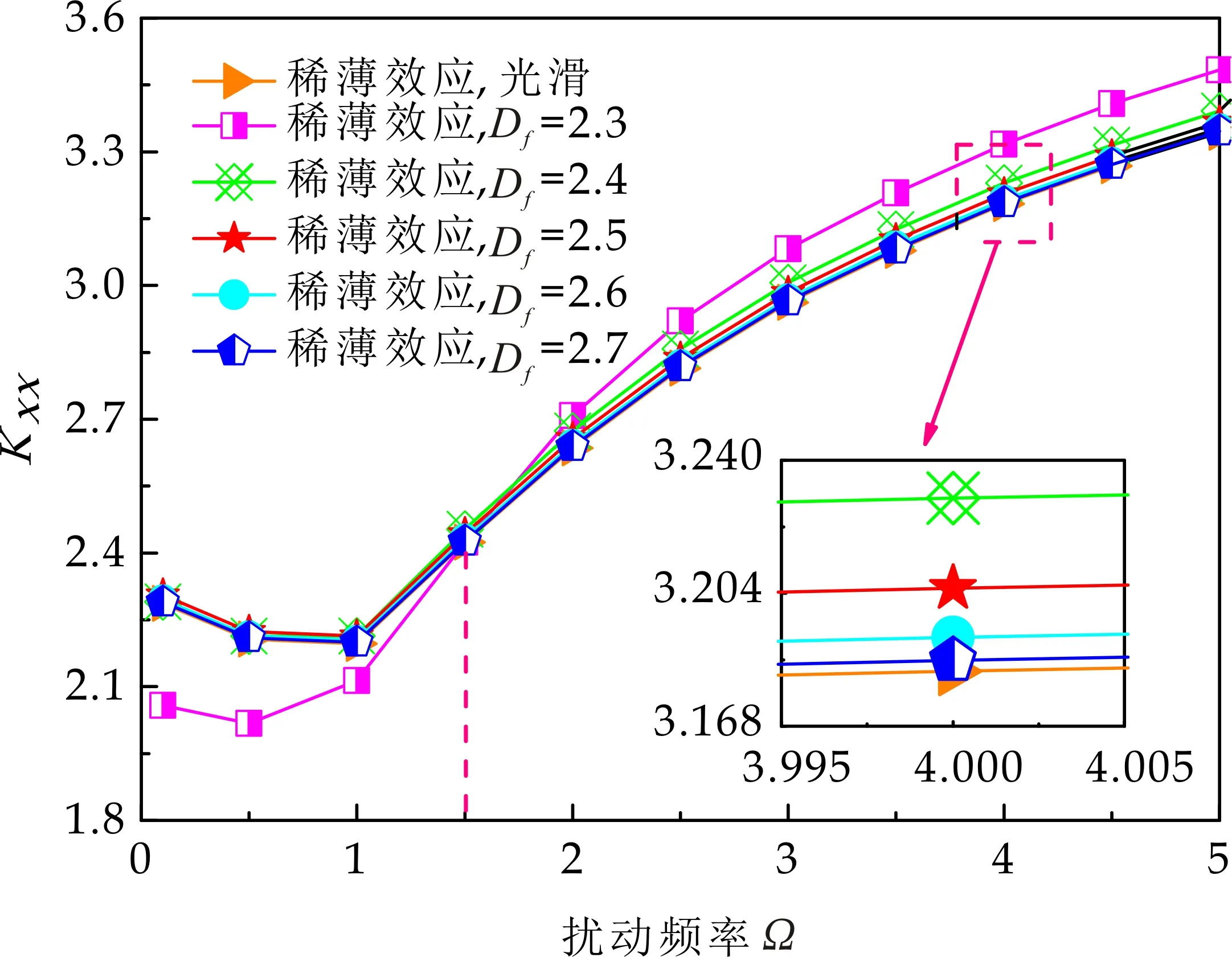
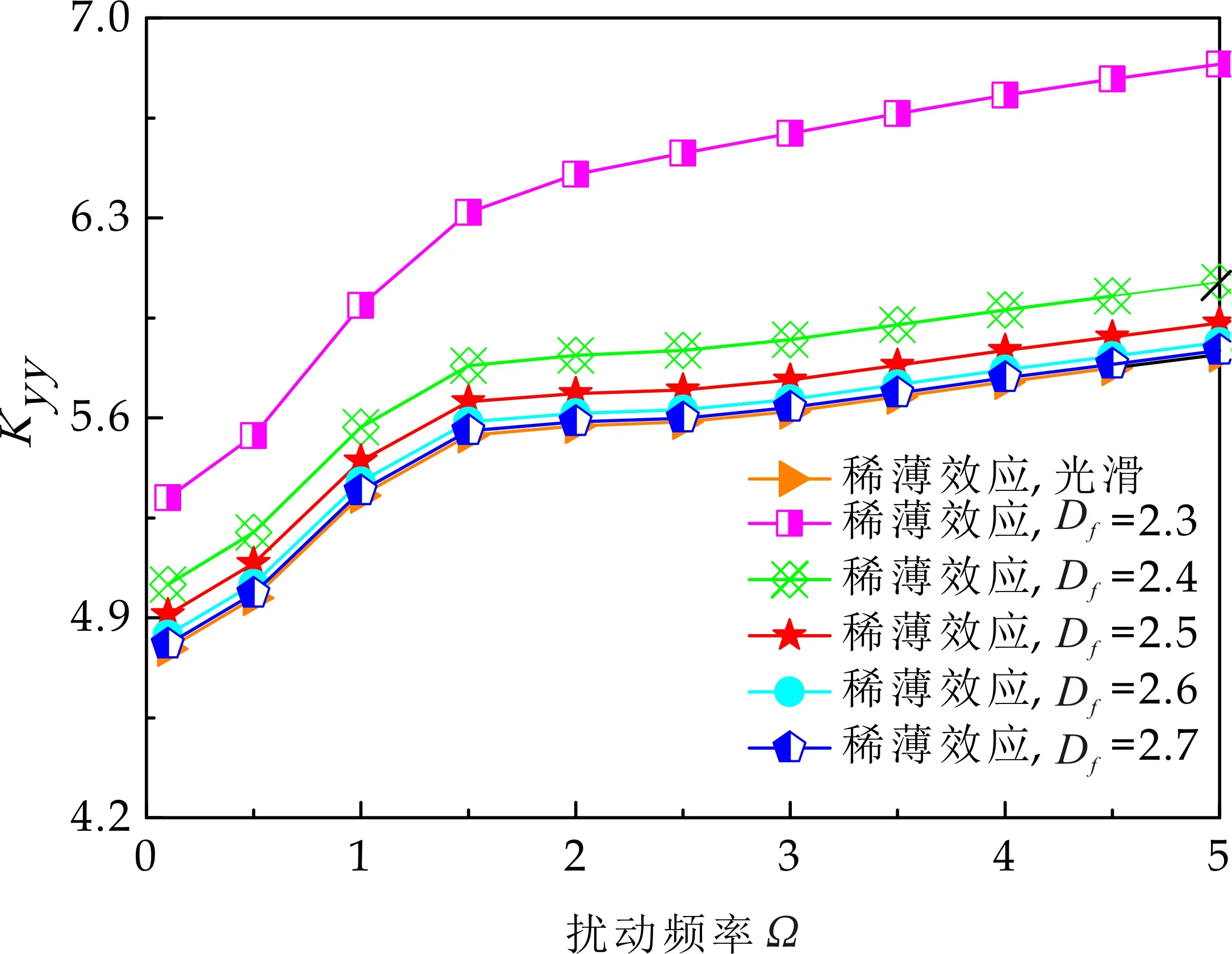
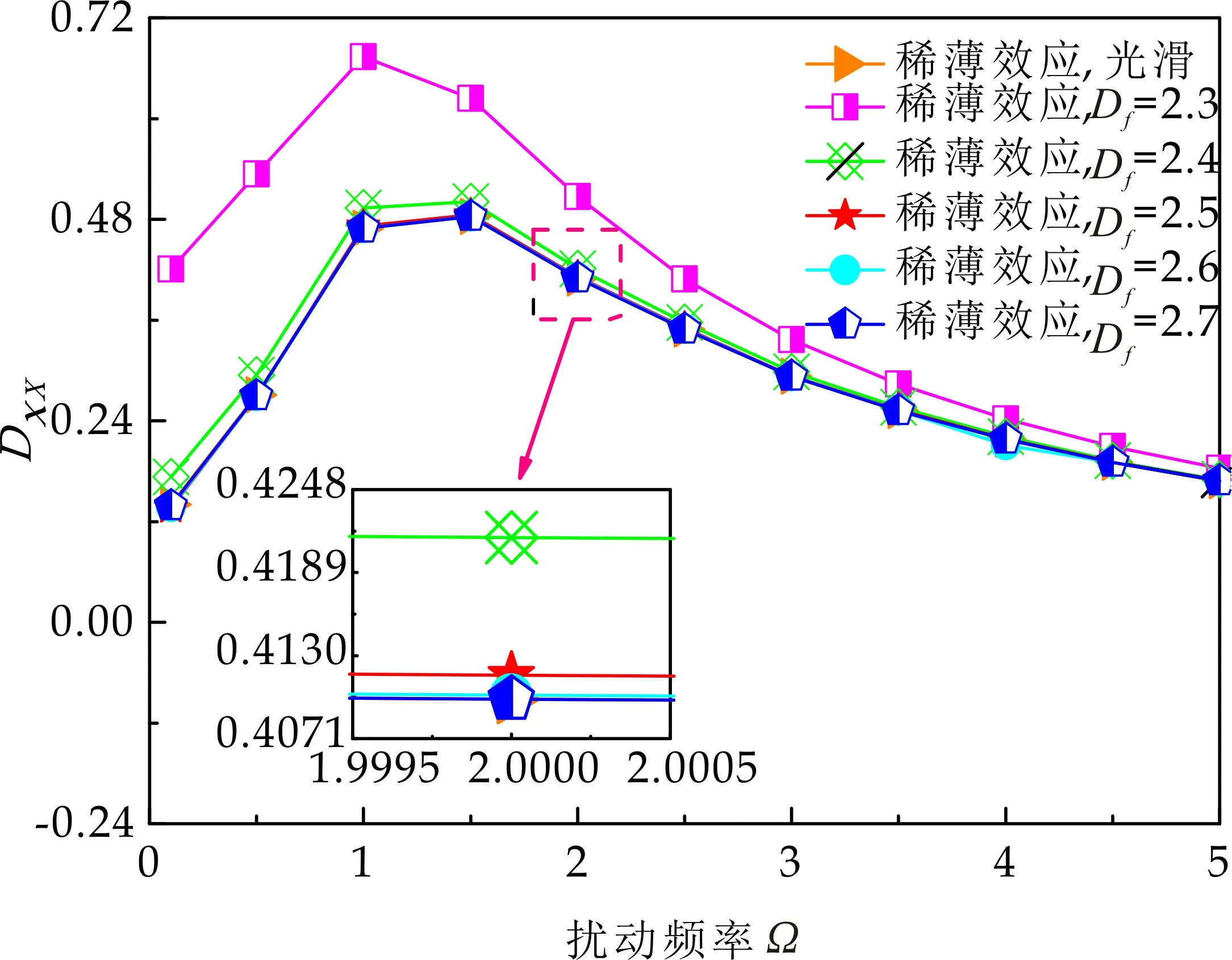
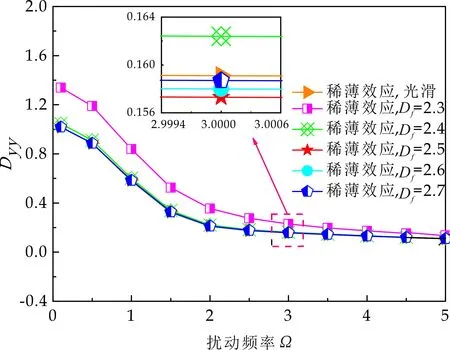
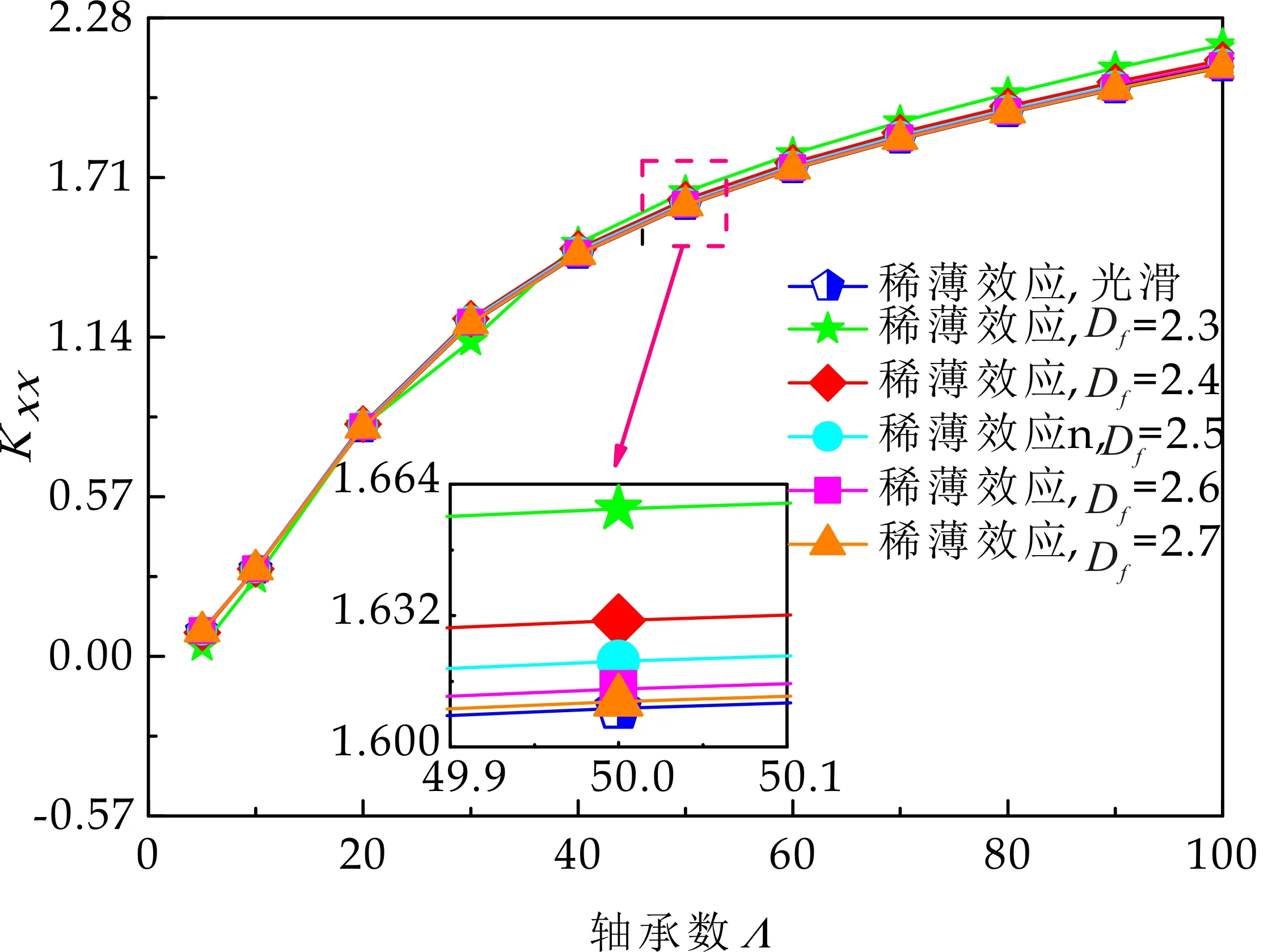
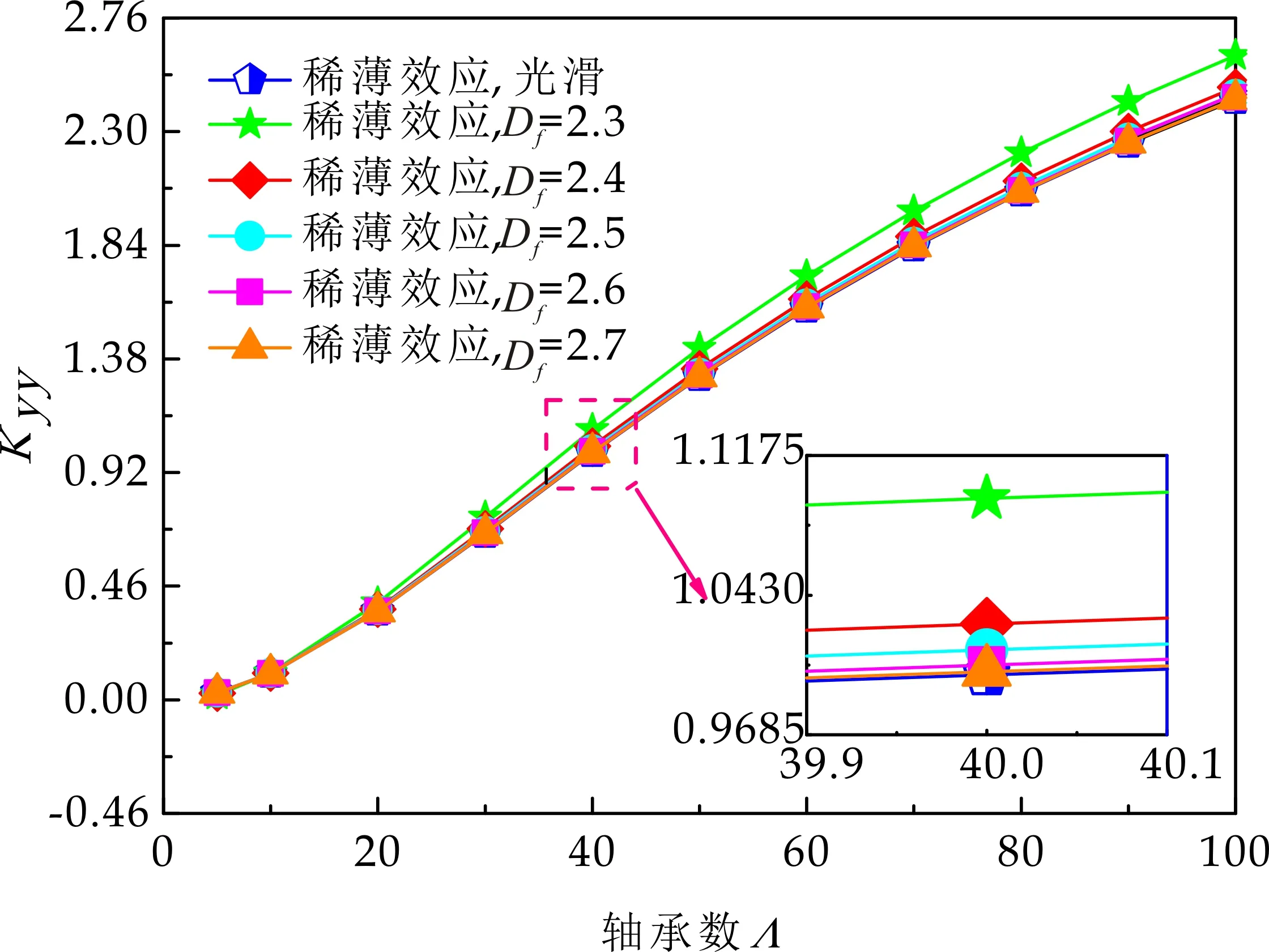
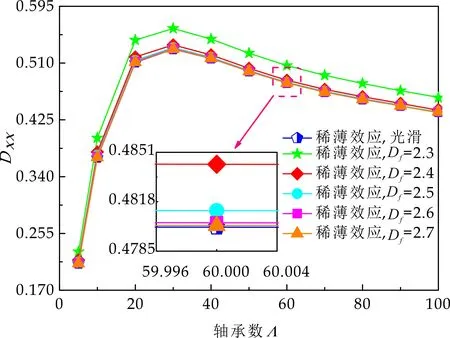
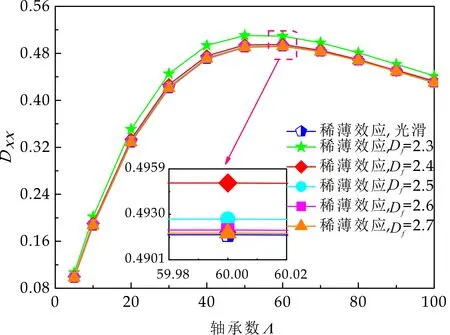
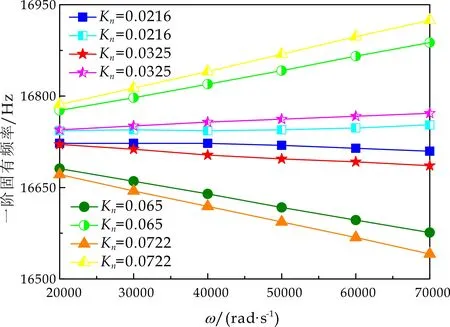
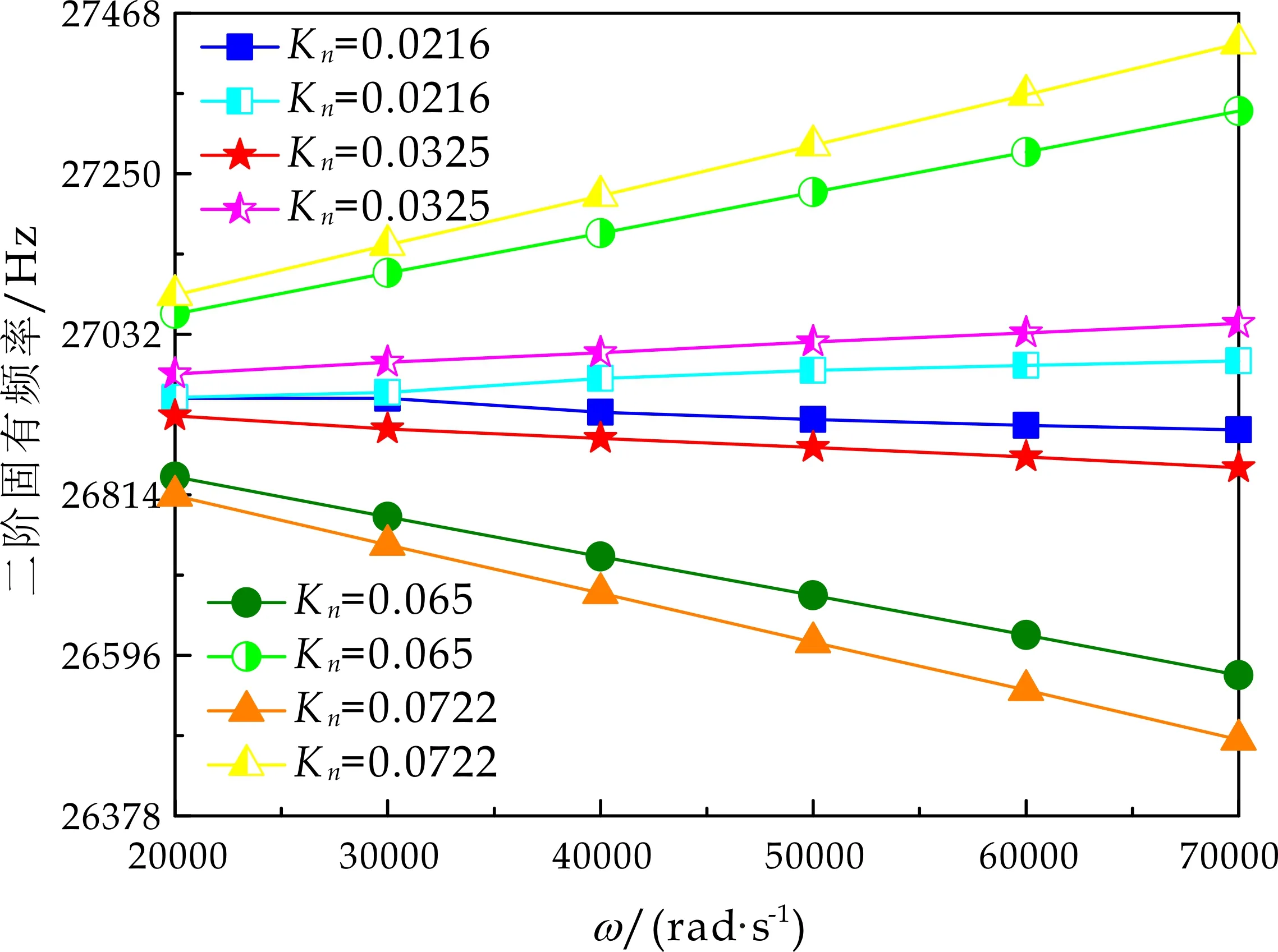
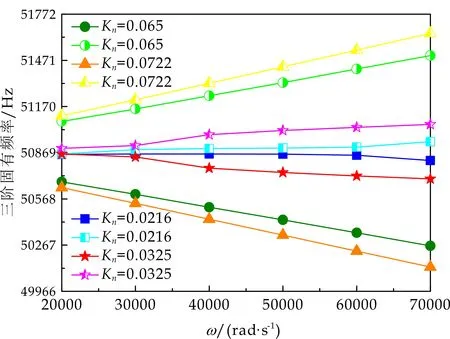
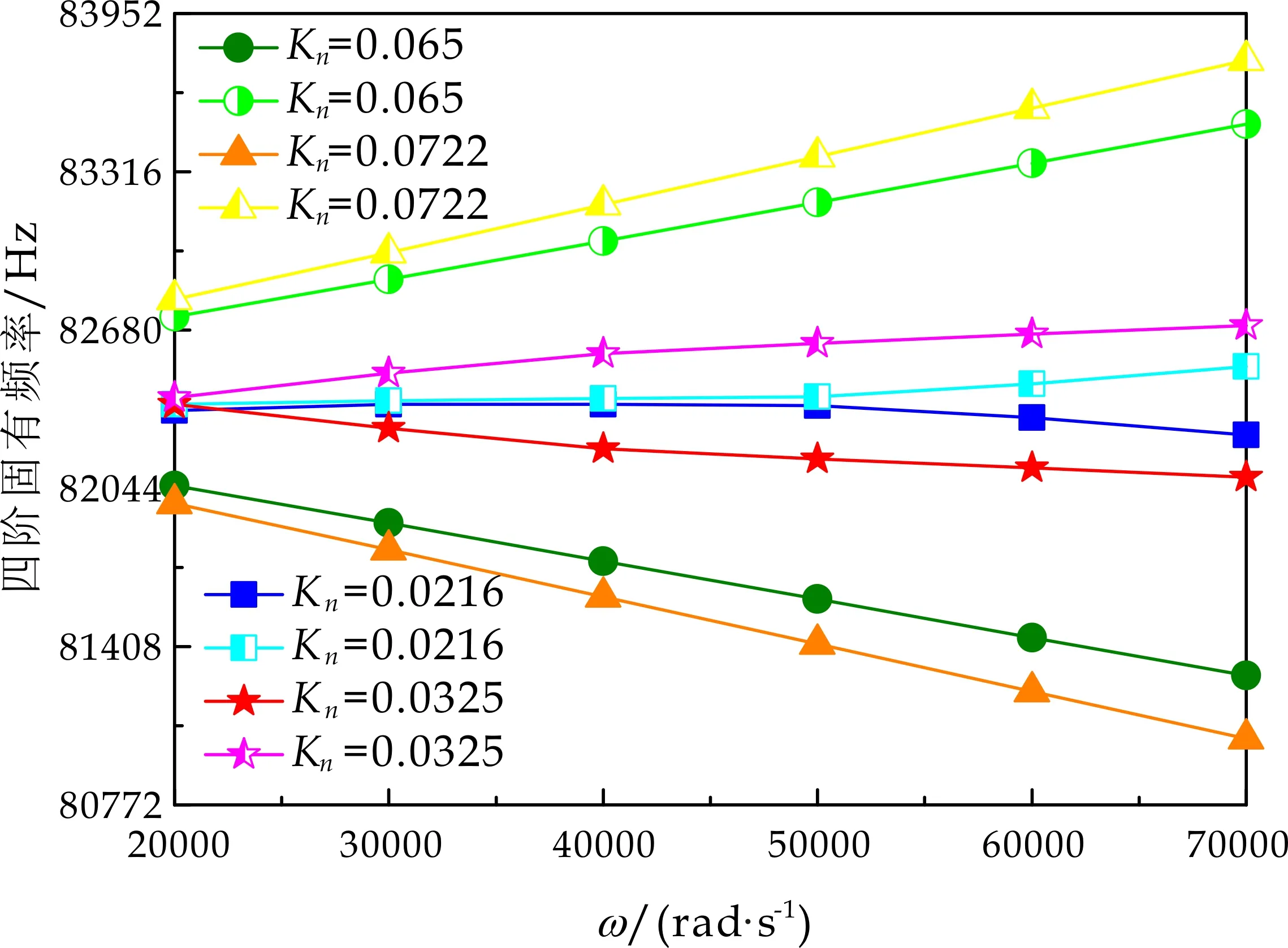
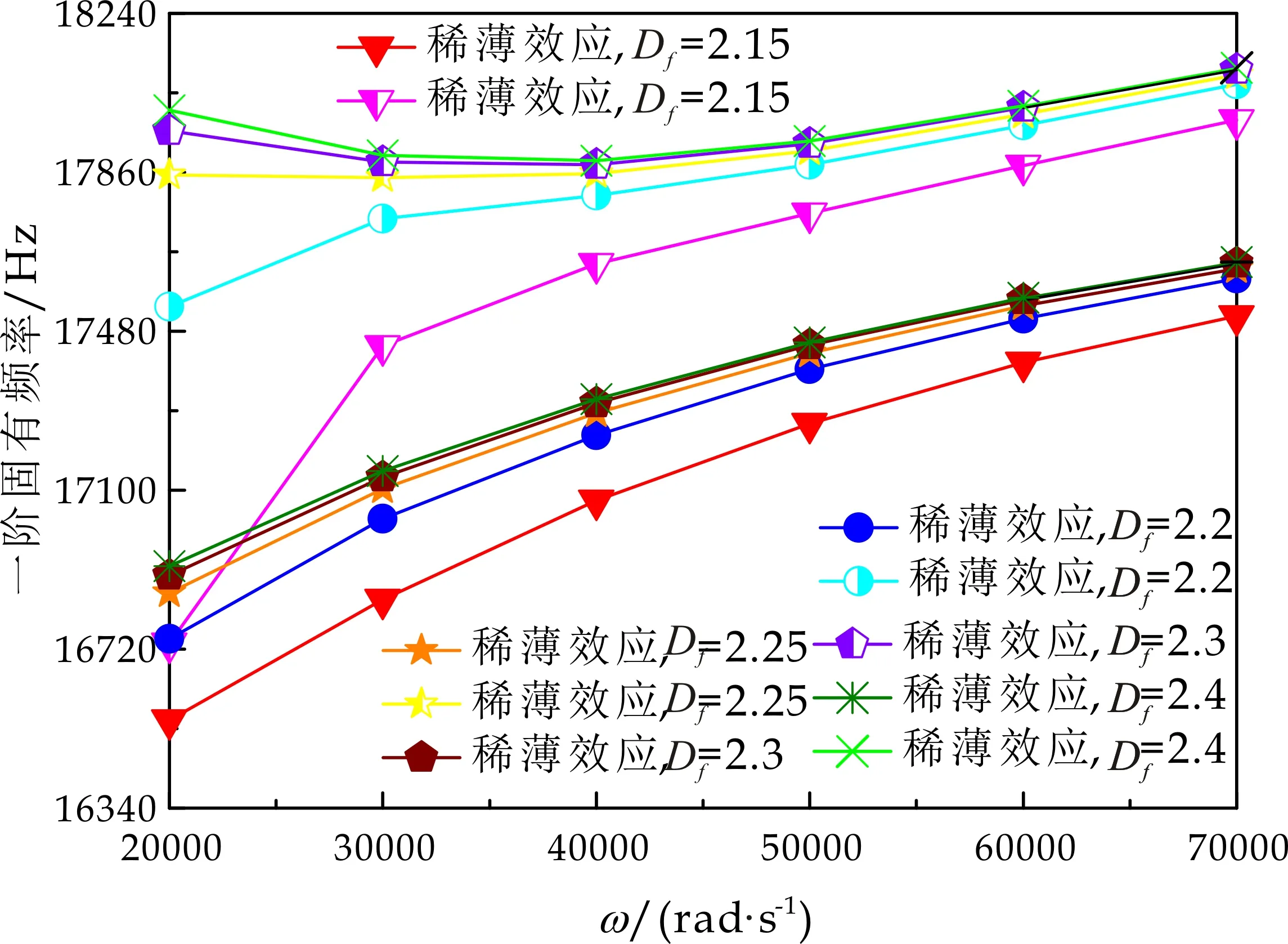
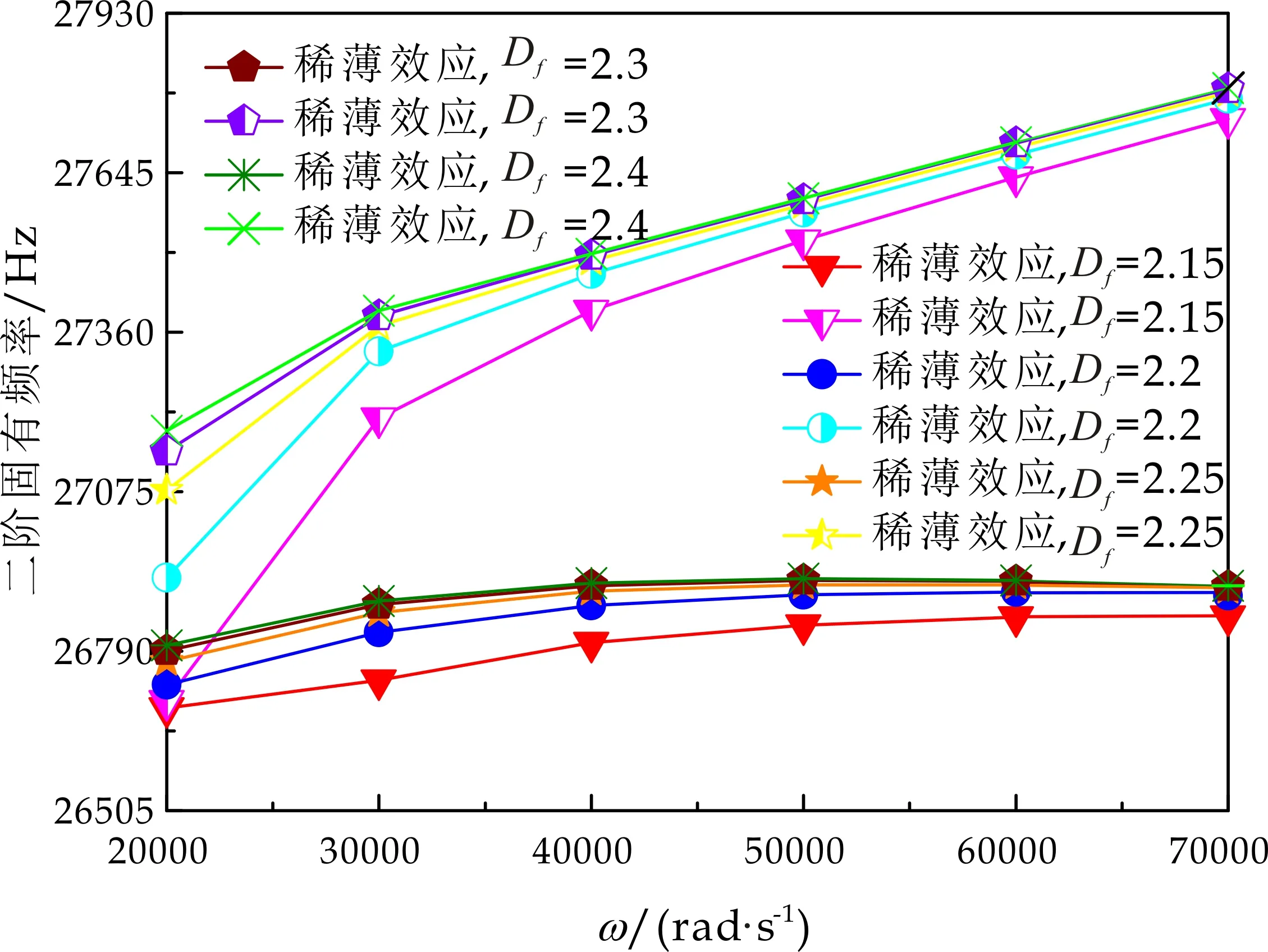
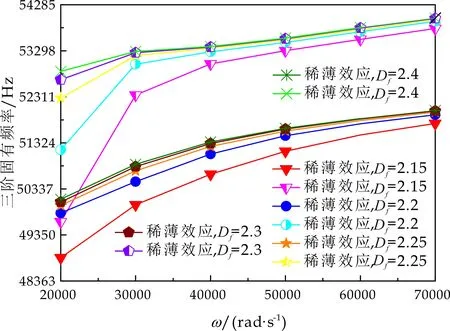
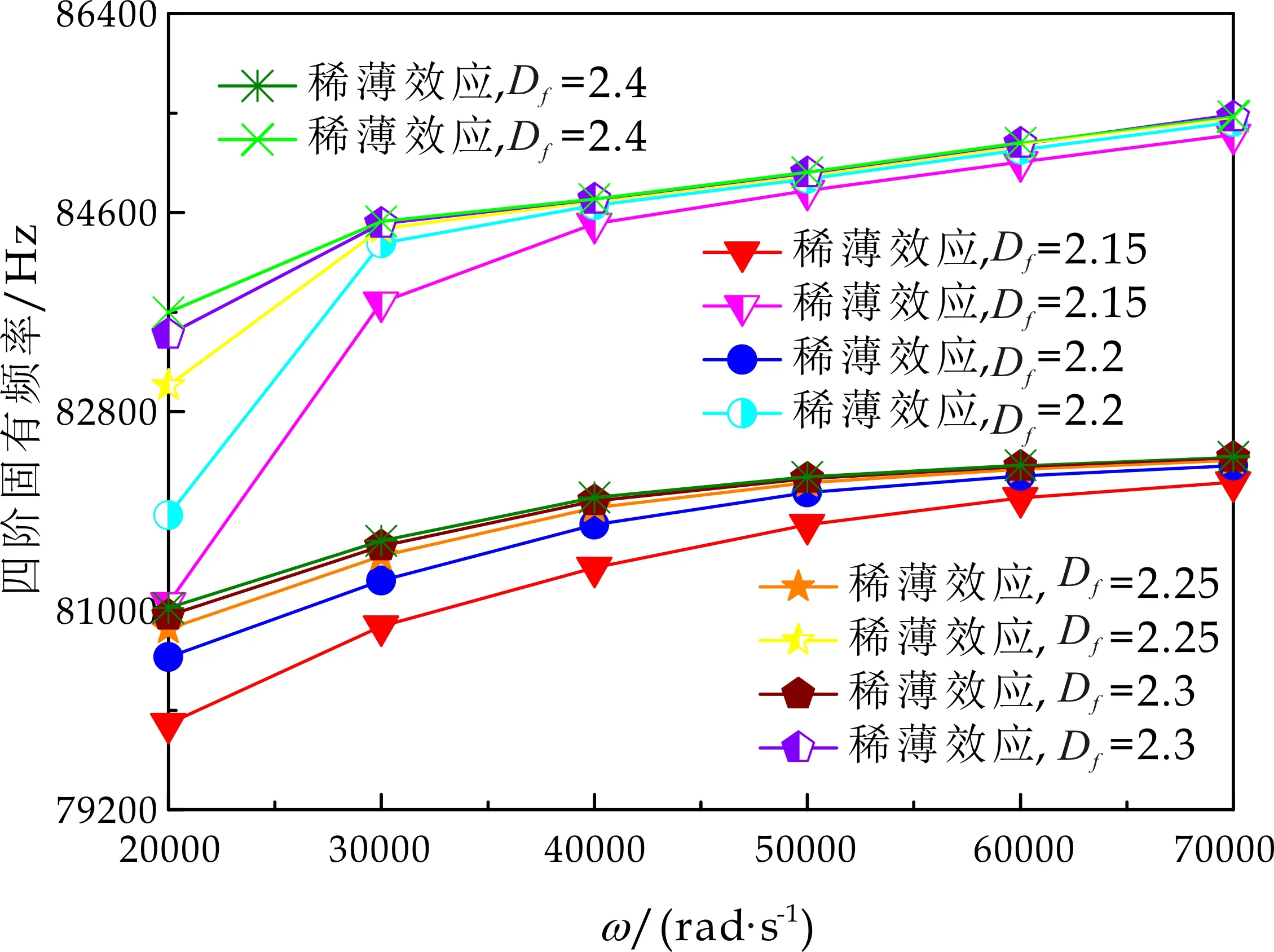
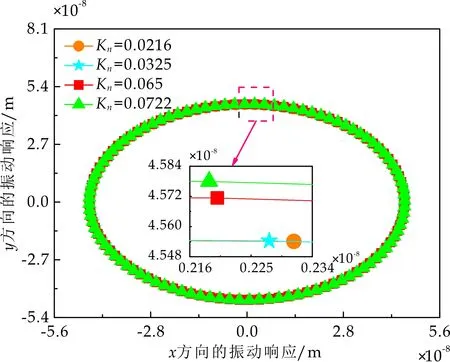
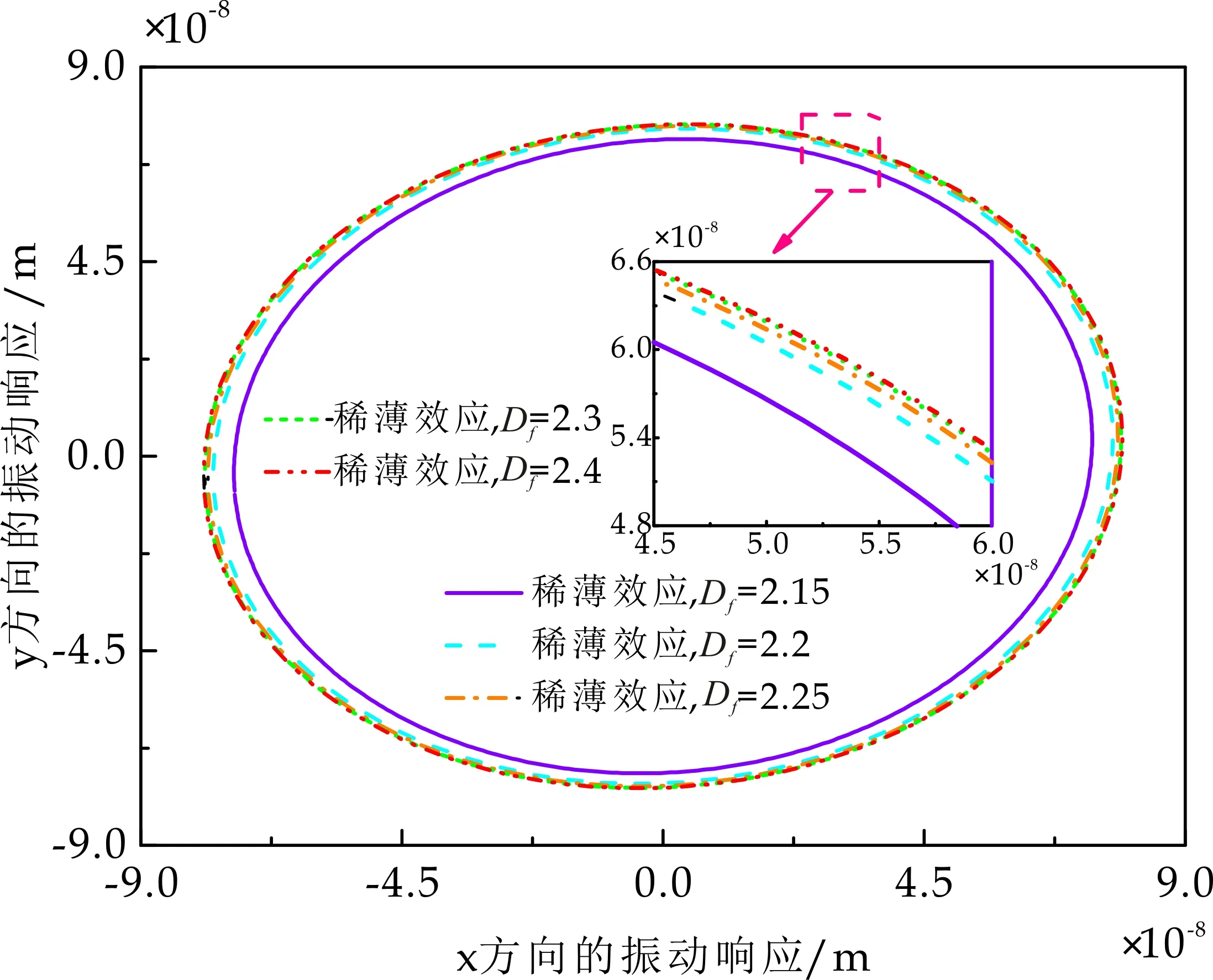
式(1)中:L为表面轮廓的样本长度;hr(x,y)为粗糙表面轮廓的微凸体高度;x,y分别为竖直和水平轮廓的位移坐标;Df为反映表面轮廓在所有尺度上不规则和复杂程度的分形维数,2 图1 (a)~(d) 为尺度系数G=1×10-10m,分形维数Df分别为2.1、2.2、2.3和2.4时三维分形粗糙表面的模拟效果.可以看出,随机表面粗糙度呈现出凹凸程度明显的不规则性,Df越小,表面微凸体峰谷高度越高,表面轮廓形貌趋于密集化和复杂化,即表面越粗糙,分形维数是改变表面粗糙度的主要参数. (a)Df=2.1,G=1×10-10 m (b)Df=2.2,G=1×10-10 m (c)Df=2.3,G=1×10-10m (d)Df=2.4,G=1×10-10 m图1 不同分形维数的三维粗糙表面形貌模拟 图2和3分别为粗糙表面微型动压气体轴承的结构示意图及三维模型图.忽略润滑膜中的惯性效应和热效应且假设可压缩气体流动为层流,考虑稀薄效应和表面粗糙度的修正Reynolds方程无量纲形式可表示为: (2) 式(2)中:Q为流量因子,H=h/Cb为无量纲气膜厚度(h为有量纲气膜厚度,Cb为轴承半径间隙),P=p/pa为无量纲气膜压力(p为有量纲气膜压力,pa为环境压力,pa=1.033×105N/m2),φ=x/R为轴承的无量纲周向角坐标(x为轴承的周向坐标,R为轴颈半径),λ=z/R为轴承的无量纲轴向坐标(z为轴承的轴向坐标),Λ=6μωR2/paCb2为轴承数(μ为气体的动力粘度,ω为轴颈转动角速度),T=ωt为无量纲时间. 图2 粗糙表面微型动压气体轴承结构示意图 图3 粗糙微型气体滑动轴承的三维模型图 流量因子Q是考虑气体稀薄效应后对气膜流量的修正项,Boltzmann修正模型[24]的表达式为: (3) 式(3)中:Kn为Knudsen数,Kn=λ0/h,λ0为气体分子平均自由程,取65×10-9m. 在各种气体稀薄效应修正模型的文献中,Boltzmann模型在较宽Knudsen数范围内较为准确,许多文献以Boltzmann模型结果作为评判标准,在超薄气膜润滑问题中应用较广. 在式(2)中的无量纲气膜厚度,包括名义光滑膜厚和随机分形粗糙度高度两部分,考虑表面粗糙度微型气体轴承的气膜厚度表达式为: H=(h0+hr)/Cb=1+εcosφ+ (4) 为得到微型气体轴承的静态润滑性能,需要先求出轴承内的气膜压力分布,通过积分得到轴承的承载能力和摩擦特性.可压缩流体润滑Reynolds方程是二维非线性偏微分方程,本文采用MATLAB偏导数方程(PDE,Partial Differential Equation)工具箱快速求解修正Reynolds方程,将超薄气膜润滑的修正非定常Reynolds方程进行数学变换,化为椭圆型偏微分方程形式: (5) 式(5)中:系数c、a、f以及未知函数ζ是定义在平面有界区域Ψ上的实(或复)函数. 令PH=S,(PH)2=S2=Π,将式(2)整理为PDE工具箱中标准偏微分方程形式进行求解[25]. (6) 求得轴承的静态气膜压力分布后,无量纲承载力和作用在轴颈表面的无量纲周向摩擦力可按以下公式计算[14]: (7) (8) 式(7)中:B为轴承宽度,W为轴承的有量纲承载力. 利用小扰动法和偏导数法对非定常状态下的修正Reynolds方程进行求解,在求解域内积分可得到微型轴承的动态刚度和阻尼系数.假设轴颈中心绕其静态平衡位置作动态周期小扰动(E,Θ),轴颈静平衡位置为(ε0,θ0),则在任意时刻轴颈位置(ε,θ)的表达式为[26,27]: (9) 式(9)中:E0为复数范围内的扰动偏心率幅值;Θ0为复数范围内的扰动偏位角幅值;Ω=ν/ω为无量纲扰动频率;ν为轴颈扰动频率;ω为轴颈转动角速度;i为虚数单位. 假设轴颈小扰动情况下轴颈和轴瓦之间的气膜压力和气膜厚度具有如下形式[27]: (10) 将式(10)代入式(2),方程左右两边消去式(2)中的项和eiΩT,得到考虑气体稀薄效应和表面粗糙度动态Reynolds方程的一般形式: (11) 在动态Reynolds方程(11)中隐含了轴颈扰动量E0和Θ0,可采用偏导数法[27]计算轴颈小扰动时微型气体轴承的动态刚度和阻尼系数Kij和Dij(i,j=x,y),参考文献[28]给出了详细的求解过程. 图4为微型气体轴承-转子系统的结构示意图.转子由两个结构尺寸完全相同的微型气体动压滑动轴承a和b支承,两个微型轴承分配的载荷相等.对称结构转子材料为镍铬钢,弹性模量E为206 GPa,泊松比υ为0.3,密度ρ为7.9×103Kg/m3,质量M为2.3 g,切变模量G为79.4 GPa.图5所示为转子系统的有限元模型,将转子划分为19个轴段,20个节点,每个节点具有4个自由度,第4和17节点是微型气体轴承的支承位置. 图4 微型动压气体轴承支承的转子系统示意图 图5 弹性转子系统的有限元模型 为方便转子系统的动力学分析,采用文献[29]详细介绍的Timoshenko连续梁理论的有限元法求解各轴段单元的运动方程,并与微型气体轴承的运动方程进行组装得到一般微型动压气体轴承-转子系统运动方程,表1给出了微型气体滑动轴承的基本参数. 表1 微型动压气体轴承的基本参数 如图6所示,利用上述理论模型计算了微型气体滑动轴承的静态性能,轴承结构参数分别为ε=0.7,B/Djo=0.075,Cb=12μm,ω=5×105r/min.并与文献[30]中无量纲气膜压力分布进行了比较,结果发现两者的数值结果基本重合且考虑轴瓦表面粗糙度时气膜压力分布呈现出随机波动的现象. 图6 微型气体轴承考虑滑移流动和表面粗糙度效应的气膜压力分布对比 图7给出了不同分形维数(Df=2.2、2.25、2.3、2.35和2.4)条件下轴承的无量纲承载力CL与偏心率ε之间的关系.由图7可知,承载系数随偏心率的增加呈现出加速上升的趋势.当分形维数从Df=2.4降低Df=2.25时,轴瓦表面粗糙度的增加提高了轴承的承载能力.这是因为随着表面粗糙度和偏心率的增加,气膜厚度不断减小,轴瓦表面的微凸体进入气膜内部,凹凸不平的轮廓对气体流动产生阻碍,减小了微型轴承两边的侧向气体泄漏,对提高轴承的承载力起到了积极的作用.当Df=2.2,轴瓦表面粗糙峰高度更高时,微型气体轴承的承载能力开始显著下降,出现这种情况是由于更加粗糙的轴瓦表面进一步降低了气膜厚度,此时气体稀薄效应对承载系数的削弱作用显著大于表面粗糙度对CL的增加作用,从而导致承载系数降低. 图7 不同分形维数下偏心率对无量纲承载力的影响(B/Djo=0.1,Λ=20,G=1×10-11 m) 图8表示ε=0.6,G=1×1010m时,不同分形维数Df下微型气体动压轴承摩擦系数-Fb随轴承数Λ的变化曲线.摩擦系数随Λ的增大呈近似线性增加的趋势,随Df值的减小,轴瓦表面粗糙度使摩擦系数的增加幅度更为明显.这是因为轴承数增强了气体动压润滑效应,提高了稀薄气流与轴颈表面的剪切应力. 图8 不同分形维数下轴承数对摩擦系数的影响 图9(a)~(d) 分别给出了不同分形维数下动态刚度和阻尼系数随无量纲扰动频率Ω的变化曲线.直接刚度系数Kxx和Kyy随扰动频率的增加而增大且Kyy远大于Kxx,这是因为气体润滑薄膜主要在竖直方向上支承轴颈的重量.可以看出,粗糙表面微型气体轴承的动态刚度系数比光滑微型轴承表面的刚度系数有所提高.当Ω>2且Df=2.3时,微型气体动压滑动轴承的动态刚度系数明显增加,这是由于轴瓦表面微凸体粗糙峰越高,沿滑动方向的Poiseuille流修正项越大,微型轴承两侧稀薄气流受到表面粗糙度的阻力越大.直接阻尼系数Dxx随Ω的增加先增大到峰值后开始缓慢下降,直接阻尼系数Dxx随微型气体轴承表面各向同性粗糙度高度的增加而增大,Dyy随分形维数Df降低先减小后急剧增加,随着扰动频率Ω的增加,粗糙和光滑微型气体轴承的阻尼系数均收敛于相同的值. (a)Kxx vs.Ω (b)Kyy vs.Ω (c)Dxx vs.Ω (d)Dyy vs.Ω图9 分形维数和扰动频率对动态系数的影响 图10 (a)~(d) 分别表示在ε=0.6,B/Djo=0.1和G=1×10-10m时,不同轴承数Λ和分形维数Df对粗糙和光滑轴瓦表面微型气体动压轴承动态性能的影响.动态刚度系数均随Λ的增加而增加.相比光滑微型气体轴承,分形维数越小,表面粗糙度效应对微型轴承动态刚度系数的增加幅度越大.直接阻尼系数均表现出随轴承数增加先增加后减小的趋势,与分形维数Df对动态刚度系数的影响相似,轴瓦表面粗糙形貌增加了直接阻尼系数Dxx和Dyy.这是因为轴承数的增加意味着轴颈旋转速度更高,显著增强的动压润滑效应和表面粗糙度效应提高了微型气体滑动轴承的动态系数. (a)Kxx vs.Λ (b)Kyy vs.Λ (c)Dxx vs.Λ (d)Dyy vs.Λ图10 轴承数对不同分形维数下动态系数的影响 图11所示为不同Knudsen数条件下转子系统前四阶固有频率随轴颈转动角速度的变化曲线.可以看出,一至四阶弯曲振动的阻尼固有频率均有2个,各阶固有频率随轴颈角速度增加均呈现出线性的变化趋势,随ω增加,每阶的2个固有频率中一个线性增加,而另一个线性降低.当Knudsen数增加时,气体稀薄程度增强,各固有频率的变化幅度更加明显,说明稀薄效应显著改变了转子系统的固有频率.图12给出了表面粗糙度对转子系统前四阶固有频率的影响,各阶固有频率均随轴颈角速度增加而增加,当分形维数从Df=2.15增加到Df=2.4时,各阶固有频率的幅值逐渐增加,说明轴瓦表面形貌粗糙度的增加会使转子系统的固有频率不断下降. (a)一阶固有频率vs.Knudsen数 (b)二阶固有频率vs.Knudsen数 (c)三阶固有频率vs.Knudsen数 (d)四阶固有频率vs.Knudsen数图11 转子系统一至四阶固有频率随Knudsen数和轴颈转动角速度的变化曲线 (a)一阶固有频率vs.Df (b)二阶固有频率vs.Df (c) 三阶固有频率vs.Df (d) 四阶固有频率vs.Df图12 转子系统一至四阶固有频率随分形维数和轴颈转动角速度的变化曲线 气体稀薄效应和表面粗糙度对微型气体轴承-转子系统节点7处轴心轨迹的影响如图13和14所示.从图13可以看出,在轴颈角速度ω=6×104rad/s时,轴心轨迹呈规则的椭圆形,转子的振幅随Knudsen数的增加而增大,这是因为气体稀薄效应降低了微型轴承的直接刚度和阻尼系数.由图14可知,当ω=7×104rad/s时,分形维数降低,即表面粗糙度峰值增加,转子的轴心轨迹逐渐变小. 图13 Knudsen数对轴心轨迹的影响 图14 分形维数对轴心轨迹的影响 本文利用Weierstrass-Mandelbrot分形函数对微型动压气体轴承随机粗糙表面进行了仿真模拟,综合考虑气体稀薄效应与表面粗糙度的耦合效应,分析了不同粗糙表面和轴承结构参数对微型气体轴承静动态性能和转子动力学特性的影响,得出以下主要规律: (1)当轴瓦表面粗糙峰谷高度较小时,气膜压力分布随轴承数和偏心率的增加而增大,微型轴承的承载能力增加.轴瓦表面凹凸不平的微凸体对稀薄气体的流动产生阻碍作用,轴颈表面摩擦力随表面粗糙度程度的增加而增加. (2)直接刚度系数随轴颈扰动频率的增加而增大,在轴承数较大时,各刚度系数均显著增大.直接阻尼系数随轴承数的增加先增大后减小.相同的扰动频率和轴承数条件下,动态系数均随分形维数的减小而增大.(3)各阶固有频率随轴颈角速度增加均呈现出线性的变化趋势.当Knudsen数增加时,各固有频率的变化幅度更加明显.微型气体轴承表面粗糙峰增加会使转子系统的固有频率下降.当Knudsen数和分形维数减小,转子的轴心轨迹逐渐变小.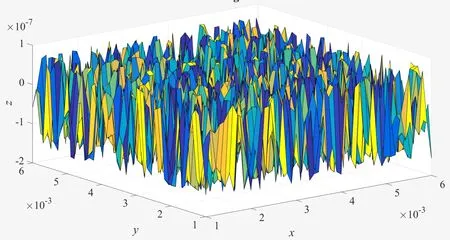
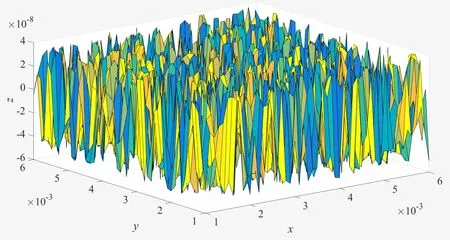
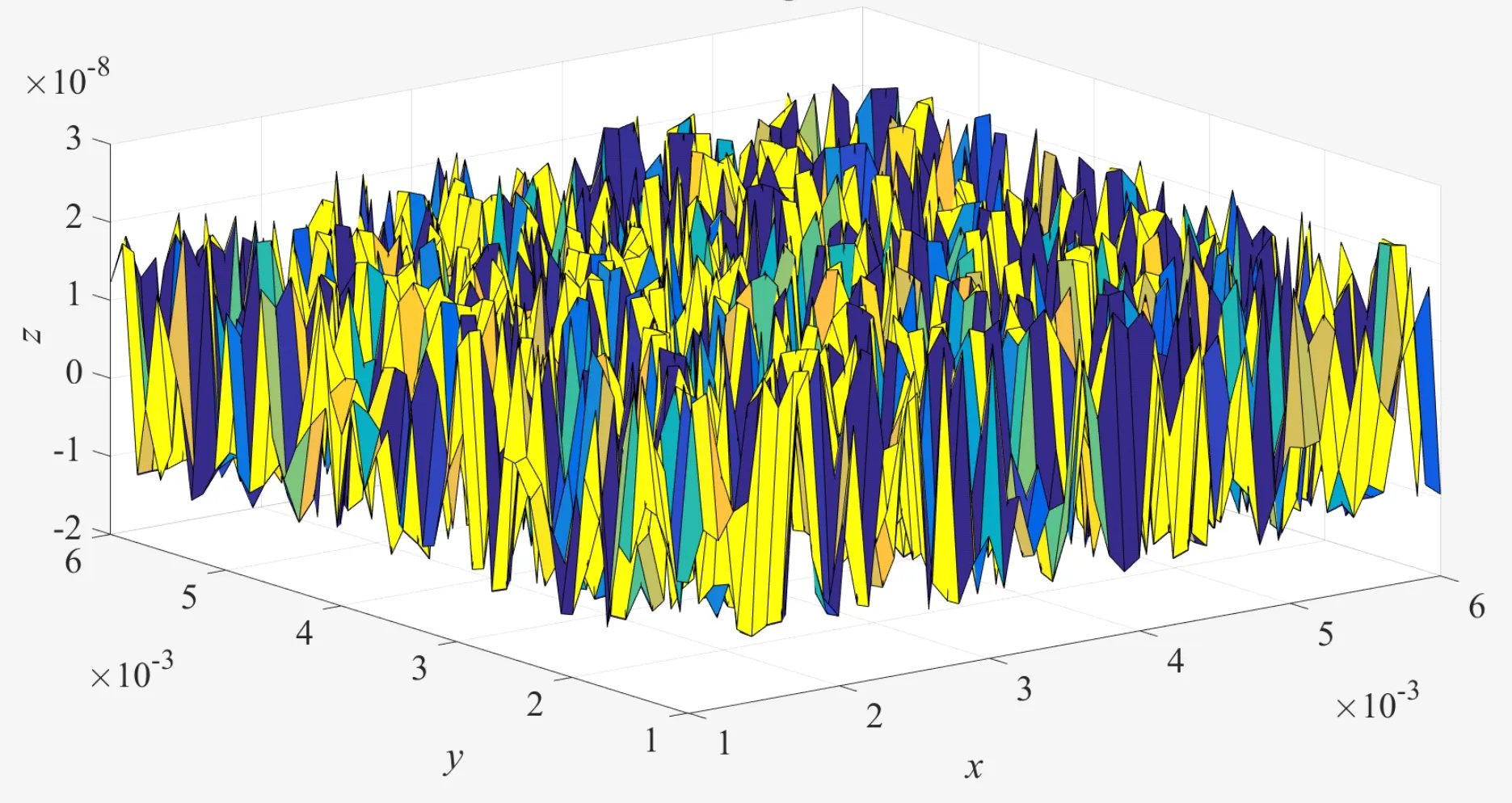
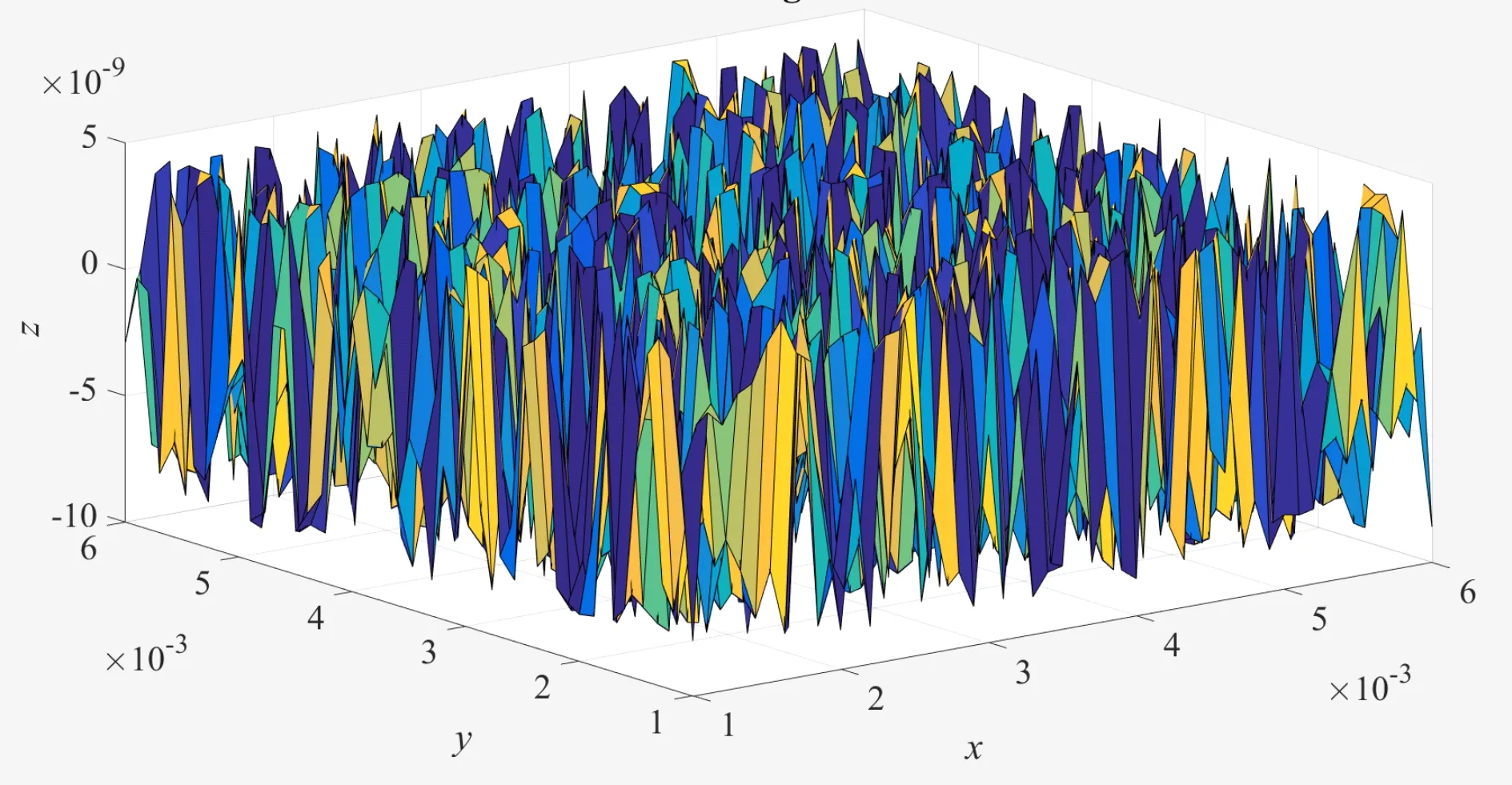
2 粗糙表面微型轴承超薄气膜润滑模型
3 稀薄气体动压润滑方程的数值求解
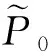
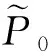
4 微型气体轴承-转子系统的运动方程


5 结果与讨论
6 结论

