双球破片冲击柱壳装药的临界起爆条件*

郭 淳，郭尚生，钱建平，顾文彬,3

(1. 南京理工大学 机械工程学院， 江苏 南京 210094； 2. 辽沈工业集团有限公司， 辽宁 沈阳 110045； 3. 陆军工程大学 野战工程学院， 江苏 南京 210007)

应用具有一定分布密度的高速破片起爆战斗部是毁伤导弹最有效的方法之一。悬浮弹幕协同反导弹药是利用其多个子弹药战斗部协同作用产生的成百上千个飞散方向任意的高速破片毁伤来袭导弹、无人机等目标的新型防御性弹药[1]。

国外学者们针对破片冲击起爆裸装药或带平板壳装药的问题已经进行了大量研究，但大多数均以单破片冲击裸装药或平板装药作为研究对象，建立了一系列经典的起爆判据，诸如：著名的非均相炸药起爆判据[2]、Held经验判据[3]、炸药的临界起爆能量判据[4]、Jacobs-Roslund经验准则[5]、Rindner经验准则[6]及Picatinny兵工厂冲击引爆解析计算式[7]等。国内学者对以上经典判据也进行了相关修正，方青等[8]基于Jacobs-Roslund经验准则，对斜碰撞问题进行了研究；张先锋等[9]在Rindner经验准则及Held研究结论[10]基础上，建立了射弹冲击起爆带壳装药经验准则；陈卫东等[11]推导了不同材质破片冲击起爆屏蔽装药的理论判据。也有少数学者针对多破片冲击裸装药的起爆判据进行了研究：李文彬等[12]提出了两破片冲击起爆裸装药的判据；梁斌等[13]基于贾宪振等[14]的双破片同时冲击起爆平板装药的规律性研究，通过数值模拟得出了多破片同时和非同时冲击起爆平板装药临界速度的变化规律。而实战环境中导弹战斗部多为柱壳装药，Xu等[15]采用量纲分析与试验结合的方法，得到单一小质量破片冲击起爆铝柱壳装药的比动能判据；江增荣[16]和王辉[17]等进行了不同尺寸单破片冲击起爆柱壳装药的试验研究；王昕等[18]在单破片起爆平板装药的Picatinny判据的基础上，通过纯数值模拟并对结果进行拟合的方法，考虑破片撞击角和装药半径的影响，提出了单破片冲击起爆柱壳装药的修正判据。

可以看出，现有公开发表的文献关于多破片对柱壳装药的起爆判据鲜有研究，所以本文将重点研究双球破片起爆柱壳装药的临界条件。本文在Jacobs-Roslund经验准则的基础上进行推导，提出考虑破片尺寸、破片撞击角度、柱壳装药的装药半径和壳体厚度的单球破片冲击柱壳装药的临界起爆条件，进而结合BoxLucas 1指数函数模型提出双球破片同时冲击柱壳装药临界起爆条件的工程分析模型，并与现有的试验和数值模拟得到的结果进行对比，验证判据的准确性和普适性。

1 临界起爆条件的建立

单破片起爆平板装药的Jacobs-Roslund经验准则[8]如式(1)所示。

(1)

其中：v′为单破片冲击起爆平板装药的临界速度(km/s)；θ为破片飞行方向与平板法线方向的夹角(°)，；H为平板厚度(mm)，而H/cosθ表示平板在破片速度方向的厚度；d为破片直径(mm)；k为尖头系数，与破片形状有关；A1为装药敏感系数，与装药和破片材料有关；B1为壳体保护系数，A1、B1的值可由试验或数值仿真拟合得到。

由于柱壳装药的装药半径的存在，柱壳装药与平板装药的差异表现在破片速度方向上的壳体厚度的不同，不能再简单地采用H/cosθ表示。下面对Jacobs-Roslund经验准则进行推导，建立更适合柱壳装药的临界起爆条件。本文提出如下假设：

1)只考虑球形破片起爆柱壳装药的情况，选用两个直径均为d且同材质的球形破片进行研究；

2)柱壳和球破片材料分别选用钢和钨合金，装药选用B炸药，忽略其材质变化引起的柱壳装药起爆差异；

3)球破片作用下柱壳装药的敏感系数A、壳体保护系数B在柱壳装药材料固定的条件下视为定值，不随柱壳装药的结构变化而改变；

4)不考虑球破片跳飞的情况；

5)球破片与柱壳装药作用过程中，忽略装药绕轴线的转动。

图1为双钨球破片同时撞击柱壳装药的示意，图中l为双球破片平行于装药轴线的球心距离，即轴向球心距。图2为过其中任意一个球破片碰撞点且垂直于装药轴线的截面示意，zi轴垂直于截面，其中i=1，2。装药半径为R，柱壳厚为Ht，钨球直径为d。由于柱壳装药的对称性，双球破片撞击位置可视为半圆柱的同一侧，即只考虑yi为正的情况。钨球速度vi与平面xioi0yi的夹角为γi，当vi平行于zi轴的速度分量方向为zi轴正方向时，γi取正，否则为负。v′i是vi在平面xioi0yi上的投影速度，v′i与壳体、装药的交点分别为Ei、Fi，撞击瞬间破片球心Oi和装药截面圆心oi0的连线oi0Oi与v′i的夹角为θi，v′i处于oi0Oi绕Oi逆时针方向时，θi取正；v′i处于顺时针方向时，θi取负。oi0Oi与yi轴的夹角为δi，yi正轴处于oi0Oi绕oi0逆时针方向时，δi取正；yi正轴处于顺时针方向时，δi取负。v′i与Eioi0的夹角为αi，θi取正时αi取正，θi取负时αi取负。v′i与Fioi0夹角的补角为βi，θi取正时βi取正，θi取负时βi取负。本文角的大小均采用角度制(°)表示。

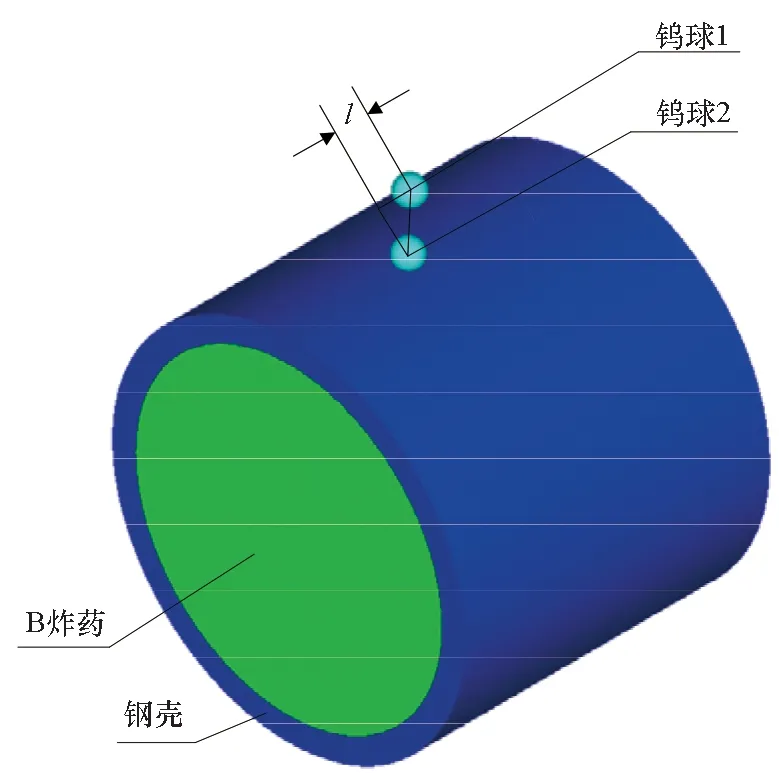
图1 双钨球撞击示意Fig.1 Schematic diagram of impacting by double tungsten fragments

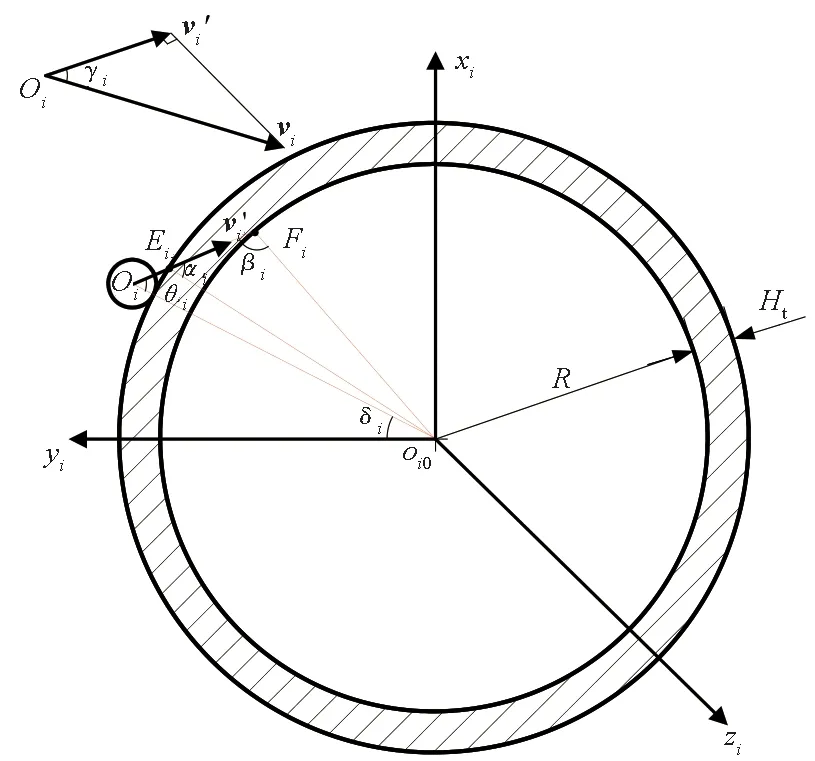
图2 截面位置示意Fig.2 Schematic diagram of cross section

在平面xioi0yi上，由三角形余弦定理可得壳体在v′i方向上的厚度ΔH′ti(即EiFi)可表示为：

(2)

式中，αi、βi还可由三角形正弦定理表示：

(3)

壳体在球破片速度vi方向的厚度ΔHti(mm)为：

(4)

因此，单球破片冲击柱壳装药的临界起爆条件可表示为：

(5)

式中：A为球形破片作用下装药敏感系数；B为球形破片作用下壳体保护系数；vi为单球破片冲击柱壳装药的临界起爆速度(km/s)。

在单球破片冲击柱壳装药的临界起爆条件的基础上，建立双球破片冲击柱壳装药临界起爆条件的工程分析模型。

设vc1、vc2分别为双钨球破片同时撞击柱壳装药的临界起爆速度；ΔHt1、ΔHt2分别为壳体在钨球1、2速度方向上的厚度；s为F1F2，即两个球破片速度方向与装药表面交点的空间距离，s可表示为：

由多破片垂直撞击平板装药的研究可以得到[13-14]，多破片在壳体表面撞击点间距离在一定范围内，撞击产生的多道冲击波叠加作用明显，即对平板装药的累积毁伤作用明显，临界起爆速度小于单破片作用的情况；而超出此范围，临界起爆速度等于单破片作用的情况，此时多破片已经没有累积毁伤效果。由双球破片同时垂直撞击平板装药的临界起爆速度随球心距的增长曲线变化规律[14]可以看出，双球破片冲击起爆平板装药的临界速度随球心距的增大而增大，当双球紧靠时取最小值，且最终趋近于单个破片作用的临界起爆速度，此变化规律比较符合BoxLucas 1指数函数模型。采用BoxLucas 1模型，并结合式(5)来表示双球破片对柱壳装药的临界起爆条件，如式(7)所示：

(7)

当vc1=vc2=vc时，式(7)可简化为：

(8)

式(8)即为双球破片同时同速冲击柱壳装药的临界起爆条件。

式(7)与式(8)可以为3、4个甚至更多个球破片累积毁伤柱壳装药的研究提供参考。通过试验或数值模拟得到不同材质球破片、柱壳和装药的A与B，式(5)、式(7)、式(8)就可扩展到任意材质球破片冲击起爆不同柱壳装药的临界条件。

2 数值模拟模型

采用AUTODYN-3D数值模拟软件，分别建立单钨球破片和双钨球冲击起爆钢柱壳装B炸药的模型(如图3(a)、3(b)所示)，均采用Lagrange网格，在AUTODYN材料库[19]选取全部材料参数。壳体和装药的网格数量分别为57 600、384 000，单钨球网格数量为4 096。

(a) 单钨球冲击模型(a) Single tungsten spherical fragment impacting model

B炸药的状态方程选用Lee-Tarver炸药点火和增长模型：

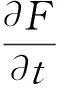
G1(1-F)cFfpy+G2(1-F)eFgpz

(9)

式中：F为炸药气体质量与炸药总质量的比值；ρ、ρ0分别为炸药当前密度、初始密度；p为炸药爆轰压力；I、b、a、x、G1、c、f、y、G2、e、g和z均为常数，具体参数详见表1。

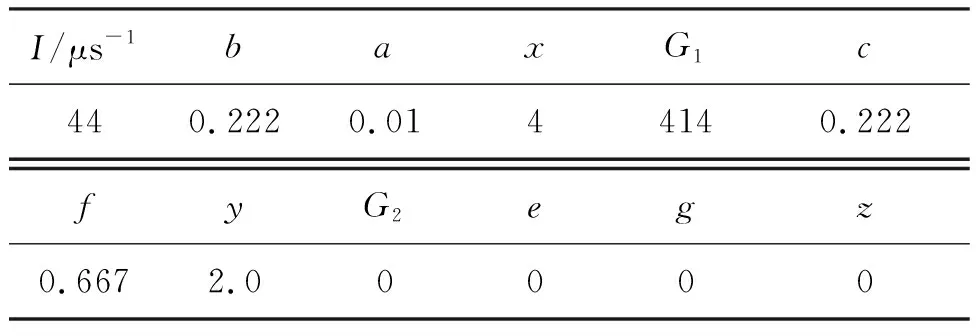
表1 B炸药材料参数

球破片和柱壳的材料状态方程、强度模型和侵蚀算法见表2。

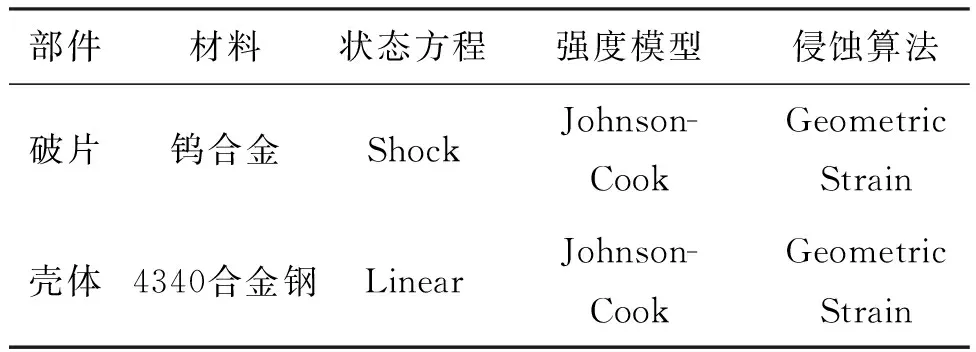
表2 破片、壳体材料模型

数值模拟以10 m/s为步长，通过“升-降法”，分别计算单钨球破片、双钨球破片冲击柱壳装药的临界起爆速度。

3 数值模拟结果与判据校验

通过数值模拟拟合得到本文选取材料的A=5.42、B=2.68，在此基础上进行单钨球和双钨球起爆柱壳装药的研究。

3.1 单钨球冲击起爆柱壳装药

作为基础先进行单钨球以不同姿态撞击柱壳装药的临界起爆条件的数值模拟。当d=7 mm、Ht=6 mm、γ1=0°，装药半径R分别为40 mm、60 mm、75 mm、100 mm，且θ1=δ1分别为0°、15°、30°、45°、55°时，得到单钨球的临界起爆速度。由数值模拟结果知道，当R=40 mm、θ1≥55°时，钨球撞击柱壳时发生跳飞，不在本文研究范围内。将不同装药半径的柱壳装药在不同θ1作用下的临界起爆速度转化为临界起爆速度v1与ΔHt1/d的关系，并与式(5)对比，如图4所示。式(5)计算结果与数值模拟结果的最大误差为4%，说明式(5)可以很好地预测单钨球以任意姿态撞击不同装药半径的临界起爆速度。而当θ1=δ1=0°时，数值模拟得到的临界起爆速度随R的变化小于0.7%，故可认为钨球以此种姿态撞击柱壳装药时，装药半径对临界起爆速度的影响很小。

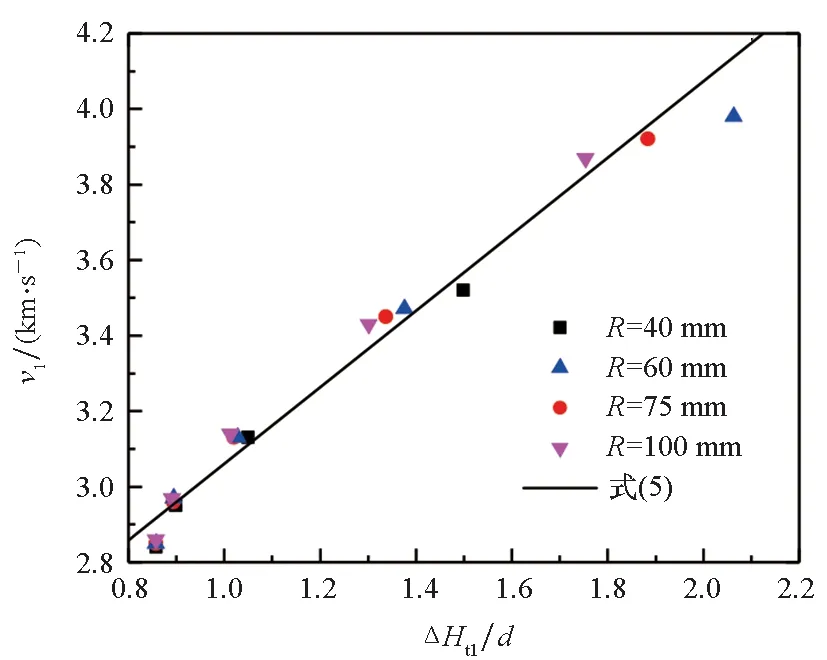
图4 临界起爆速度v1随ΔHt1/d变化的数值模拟结果与理论计算的对比Fig.4 Critical velocity v1 versus ΔHt1/d between simulation and analytical results

将现有的试验结果与式(5)的计算结果相对比：当d=7.6 mm、Ht=6 mm、θ1=δ1=0°时，式(5)得到临界起爆速度为2.73 km/s，文献[16]的试验值为2.676 km/s，误差为2.02%；当d=7 mm、Ht=3 mm、θ1=δ1=0°时，式(5)得到临界起爆速度为2.48 km/s，文献[17]的试验值为2.463 km/s，误差为0.69%。由此可以看出，式(5)能较好地预估单钨球冲击钢柱壳装B炸药的临界起爆条件。

把单钨球冲击起爆柱壳装药作为研究双钨球起爆柱壳装药的基础，可以方便获得对应双钨球中任意一个撞击位置的单钨球冲击起爆柱壳装药的临界速度。

3.2 双钨球冲击起爆柱壳装药

由于柱壳装药柱面的存在，研究双钨球撞击柱壳装药可分为两种情况：一是ΔHt1+ΔHt2为定值时，双钨球同速撞击的临界起爆速度vc随s/d的变化；二是ΔHt1+ΔHt2为变量时，双钨球同速撞击的临界起爆速度vc随s/d和ΔHt1+ΔHt2的变化。

当ΔHt1+ΔHt2为定值时，取d=7 mm、Ht=6 mm、γ1=γ2=0°、θ1=δ1=θ2=δ2=0°，装药半径R分别为40 mm、75 mm、100 mm、∞(平板装药)，得到双钨球同速的临界起爆速度随s/d的变化和式(8)曲线的对比如图5所示。由图5可以看出，此种情况下，柱壳装药的装药半径对临界起爆速度影响不大，但与平板装药还是略有差异。由数值模拟结果得到，当s≤3.5d时，柱壳装药相对于同厚度的平板装药更难以起爆，这是由于此时冲击波在柱壳装药传播过程的损耗比在平板装药中多。当s>3.5d时，双钨球对于柱壳装药的临界起爆速度等于单钨球作用柱壳装药时的情况，而此时的临界起爆速度并没有达到单个钨球起爆平板装药的临界速度。随着s的继续增加，双钨球冲击柱壳装药的临界起爆速度保持持平，而双钨球冲击平板装药的临界起爆速度则继续增加，最终趋于单个钨球起爆平板装药的临界速度。所以s>3.5d时，双钨球对柱壳装药已经没有累积毁伤作用，而双钨球对平板装药依然有累积毁伤作用。式(8)计算结果与数值模拟结果的最大误差为2.92%，式(8)可以较好地预测当ΔHt1+ΔHt2为定值时的双钨球同速撞击柱壳装药的临界起爆速度，同时也可以预测双钨球撞击平板装药的情况。

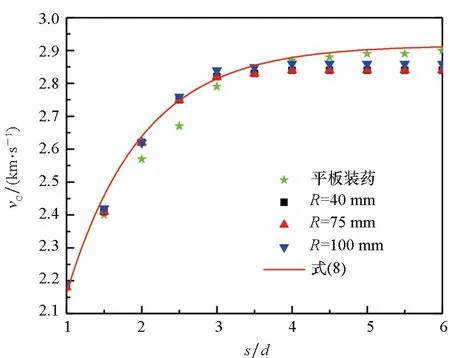
图5 临界起爆速度vc随s/d的变化关系Fig.5 Relation between vc and s/d

当ΔHt1+ΔHt2为变量时，取d=7 mm、Ht=6 mm，θ1=δ1=-θ2=-δ2分别取5°、10°、15°、20°，γ1=γ2=0°，l=0，装药半径R分别为40 mm、60 mm、75 mm、100 mm，得到双钨球同速的临界起爆速度vc随s/d和(ΔHt1+ΔHt2)/d的变化与式(8)曲面的对比如图6所示。式(8)计算结果与数值模拟结果的最大误差为2.7%，式(8)依然可以较好地预测双钨球同速撞击的临界速度vc随s/d和(ΔHt1+ΔHt2)/d的变化。

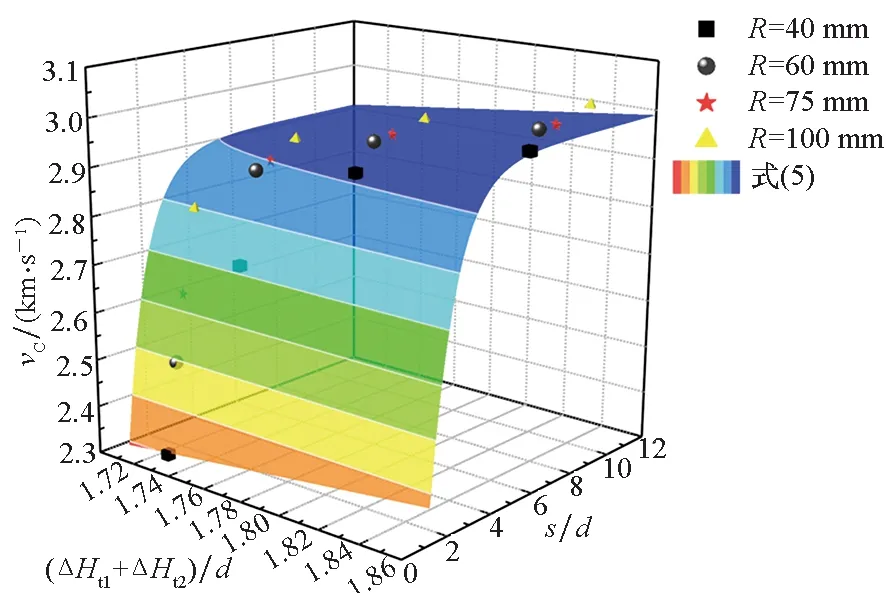
图6 临界起爆速度vc随s/d和(ΔHt1+ΔHt2)/d的变化关系Fig.6 Relation between vc with s/d and (ΔHt1+ΔHt2)/d

为了进一步验证双钨球冲击柱壳装药临界起爆条件是否具有普适性，开展不同直径钨球破片、不同壳体厚度、不同撞击角度和双钨球破片异速时的数值模拟，并与式(7)的计算结果进行比较，如表3所示。通过表中工况7和8可以看出，在保证除了速度大小之外撞击条件完全相同的情况下，v1和v2可以是两个相等的速度，亦可是两个相差较大的速度，只要保证v1+v2的值接近式(7)的计算结果就可满足柱壳装药临界起爆条件。式(7)的计算结果与数值模拟结果的误差ε均在7%以内，可以认为式(7)具有较好的普适性，可以适用于计算不同尺寸的双球形破片以任意撞击角度同速或异速且同时冲击不同尺寸柱壳装药的临界起爆条件。

4 结论

本文在单破片冲击起爆平板装药临界条件的基础上，分别建立了更符合实战情况的单球破片和双球破片冲击柱壳装药临界起爆条件的工程分析模型，并将该模型计算结果与数值模拟、现有试验对比，得到以下结论：

1)单球破片冲击柱壳装药临界起爆条件的工程分析模型计算结果与数值模拟结果对比最大误差为4%，而该模型的计算结果与现有试验对比得最大误差为2.02%，表明式(5)可以较好地预测单球破片以任意角度撞击柱壳装药的临界起爆条件。

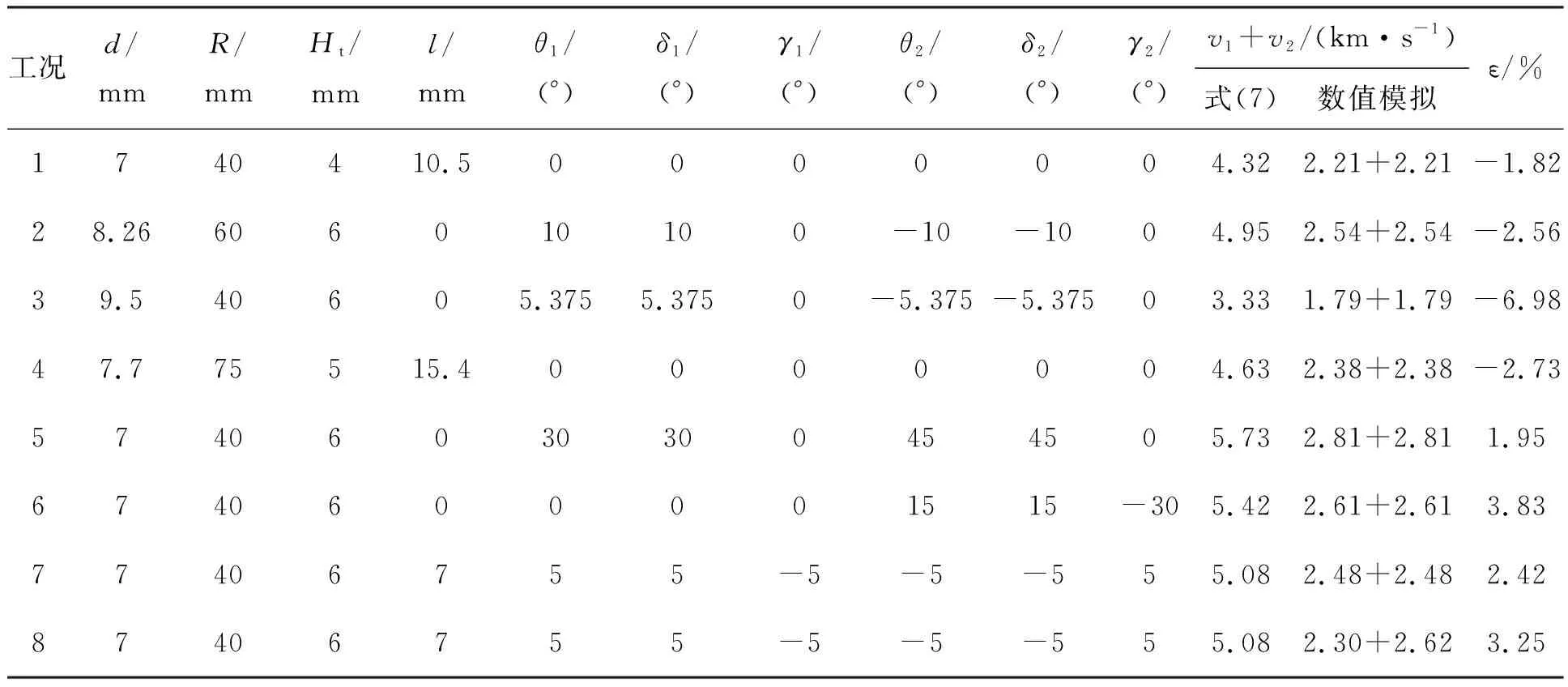
表3 临界起爆速度数值模拟与理论计算的对比

2)双球破片冲击柱壳装药临界起爆条件的工程分析模型计算结果与数值模拟结果误差小于7%，表明式(7)能较好地预测双球破片同时以任意角度撞击柱壳装药的临界起爆条件。

研究结果可为反导弹药战斗部设计和多破片对导弹战斗部的累积毁伤研究提供参考。