具有混合执行器故障和多未知控制方向的多智能体编队系统自适应协同容错控制*
张 普,薛惠锋,高 山,左 轩
(西北工业大学 自动化学院, 陕西 西安 710129)
过去十几年,多智能体系统的协同容错问题吸引了大批学者的广泛研究[1-6]。需要指出的是,随着多智能体系统复杂程度的不断加深以及控制规模的不断扩大,其不可避免地具有更多的未知不确定性、多变量特性以及更频繁的系统故障,从而严重影响编队系统的高性能动态特性。例如,当多智能体系统的模型参数不准确时,会直接影响控制效果。同时,如果不能及时排除系统故障,尤其是执行器故障,就可能使整个系统失效、瘫痪以及造成人员、财产的巨大损失,甚至导致灾难性后果。尽管这些问题过去一段时间已有了很多研究成果,但这些难题依然是开放的。
为了补偿系统中执行器故障和解决未知控制方向的问题,已有多种基于现代控制理论的方法用于解决上述问题。目前,执行器故障问题大多基于某种故障模型进行研究[7-15]。系统未知控制方向问题则采用Nussbaum函数法,用于解决未知控制增益符号问题[16]。文献[17-24]采用传统的Nussbaum函数方法解决了一种非线性系统的未知控制增益问题,但其均假设了系统中的所有控制增益均未知。文献[25]采用分数阶Nussbaum函数解决混沌系统的不同多未知控制增益问题。文献[8,26]用一组Nussbaum函数方法解决了非线性系统的多个不同未知控制增益问题。文献[9]将Nussbaum函数与滤波器相结合,利用滤波器解决Nussbaum函数缺少足够反馈信号的问题。文献[27-28]用分段Nussbaum函数方法解决部分控制增益未知的情况,但其假设未知部分的控制增益为正数。然而,上述方法仍存在问题,有些方法解决的是非线性系统仅存在同方向的部分控制增益未知问题,或者同方向的控制增益完全未知的问题,这两种情况均不能反映实际系统所面临的问题。在实际系统中,部分控制增益未知,部分控制增益已知。综上可知,目前鲜有同时研究具有混合执行器故障和部分不同未知控制增益问题的研究。
基于以上研究不足与现有研究的挑战,本文针对一类有向通信拓扑下,具有混合执行器故障和部分不同未知控制方向的非线性多智能体系统的“领航者-跟随者”一致性问题,提出了一种新颖的鲁棒自适应模糊协同容错控制方案。
1 预备知识
1.1 图论
假设3:领航者的状态及其导数均为有界的。
1.2 Nussbaum函数
如果N(τ) ∶R→R具有如式(1)所示的性质,则称N(τ)为Nussbaum函数。
(1)
同时,为了解决多未知控制方向问题,给出如式(2)所示的定义。
(2)
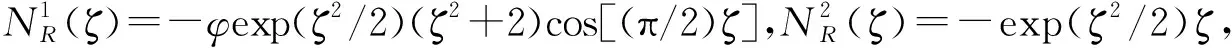
引理1[22]如果V(t)是定义在[0,ζ)的正定函数,且V(0)是有界的,有如式(3)所示不等式成立。
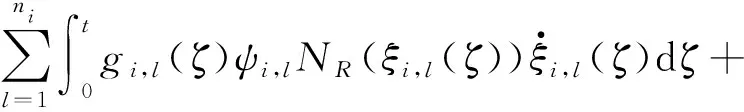
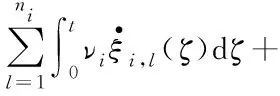
(3)
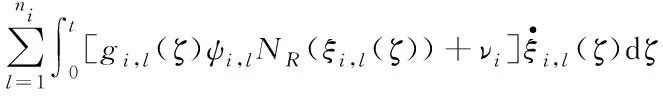
1.3 模糊逻辑系统
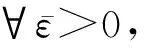
(4)
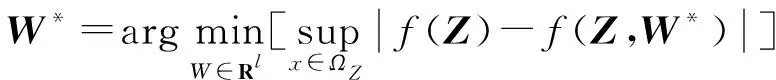
1.4 其他相关理论和引理
(5)
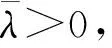
引理4[30]对于∀x≥0,∀y≥0,p∈R+,q∈R+, 同时满足1/p+1/q=1:
(6)
引理5[25]引入一阶滑模微分器的设计,如式(7)所示:
(7)
2 问题描述
2.1 系统模型
考虑同构智能体编队系统每个子系统的模型可描述为:
(8)
2.2 故障模型
为了更好研究实际系统中含有的混合执行器故障,将系统模型式(8)中的故障模型类型进行分类,如式(9)所示。
(9)
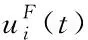
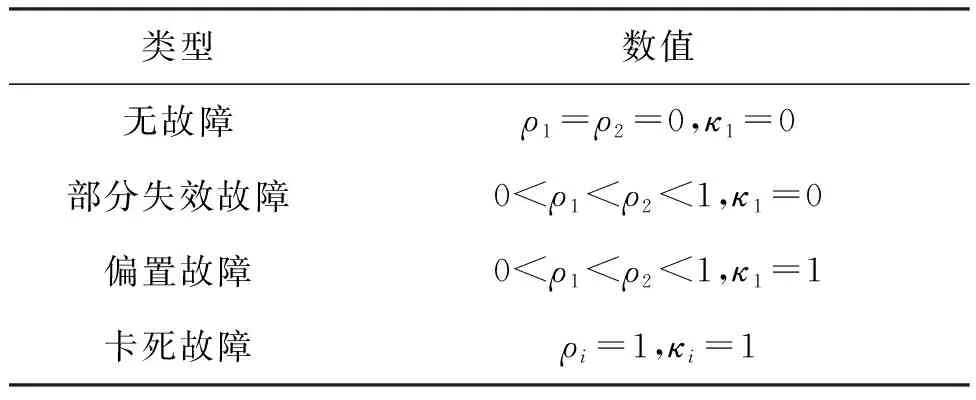
表1 执行器故障类型
3 控制器设计
在本节中,针对具有混合执行器故障式(8)和多未知控制方向式(2)的非线性多智能体系统,基于鲁棒自适应模糊技术设计一种新颖的协同容错控制器。
定义同步误差:
(10)
其中:aij表示第i个智能体与第j个智能体之间通信的权重系数;bi表示领航者和跟随者的节点增益;e1=[e1,1,e2,1,…,eN-1]T∈RN。
根据图论,式(10)可进一步重写为:
(11)
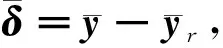
联立式(8)和式(10),采用反步技术,可得:
(12)
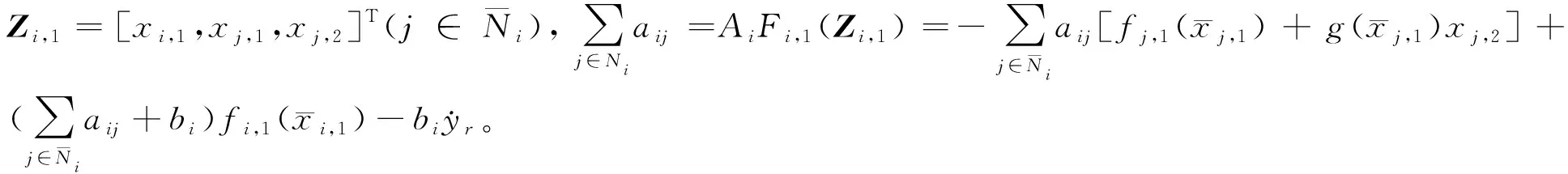
利用模糊逻辑系统对Fi,1(Zi,1)逼近,可得:
(13)
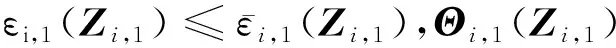
根据Young′s不等式,联立式(12)和引理3,可进一步得出:
构建Lyapunov函数:
(15)
式中,Γi,1表示正定矩阵,ηi,1表示待估计参数。
对式(15)求导,结合式(12),可得:
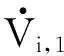
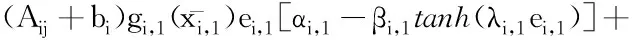
(16)
由式(16)可得虚拟控制律及对应的更新律。
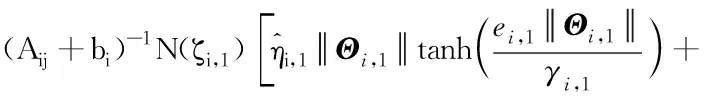
(17)
(19)
将式(17)~(19)代入式(16),可得:
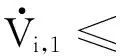
在小组学习过程中,教师要懂得收放自如,对学生的学习要给予有力的指导和支持。在学习中,学生们难免会遇到各种困难,教师要真正给予学生有效的点拨,这样当学生在小组合作学习中产生激烈的争执,或者找不到前进的方向时,教师就能够从更高的层次给学生一定的提示和引导。在平时的教学工作中,教师也要注意思想方法的渗透,让学生真正学会学习,而不是被动地跟着老师的思路按部就班地学习。
(20)
将式(18)代入式(20),可得:
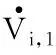
(21)
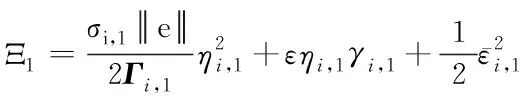
(22)
式(22)两边同乘以eci,1t,可得:
对式(23)两边同时积分,则有:
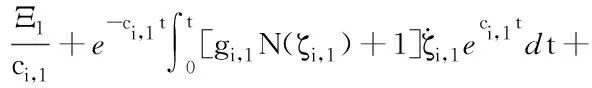
(24)
第k步(2≤k≤ni-1):定义误差,如式(25)所示。
(25)
(26)
(27)
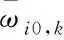
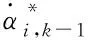
(28)
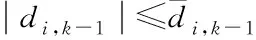
将式(28)代入式(26),可得:

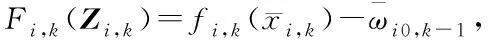
(30)
构建Lyapunov函数:
(31)
对式(31)求导,结合式(29)和引理4可得:
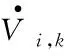
(32)
由式(32)可得虚拟控制律和更新律,如式(33)~(35)所示。
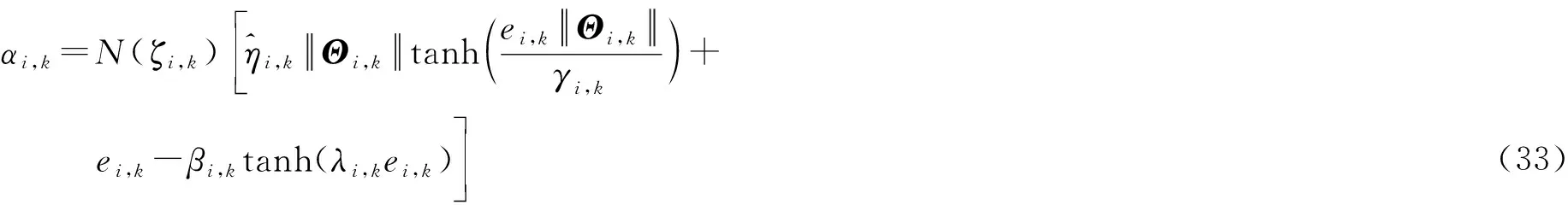
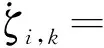
ei,kβi,ktanh(λi,kei,k)
(34)
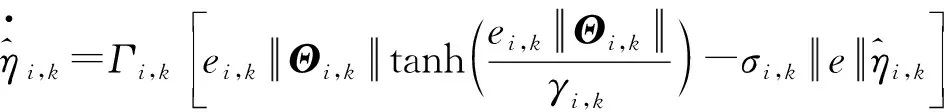
(35)
将式(33)~(35)代入式(32),可得:
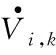
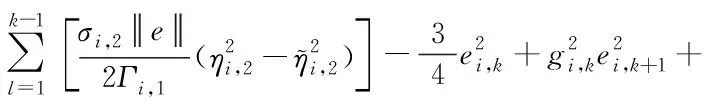
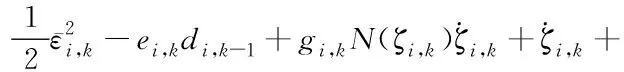
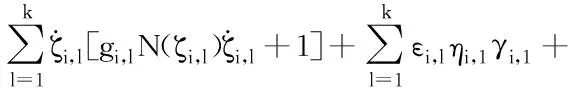
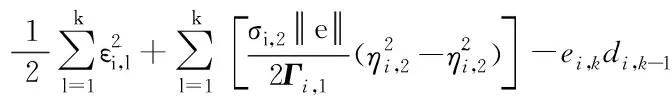
(36)
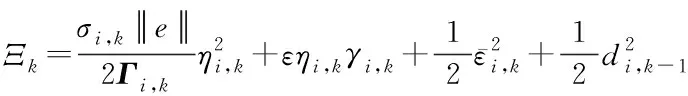
式(37)两边同乘以eci,kt,可得:

对式(38)两边同时积分,可得:
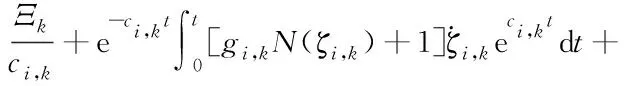
(39)
第N步:定义误差,如式(40)所示。
ei,ni=xi,ni-αi,ni-1
(40)
对式(40)求导,结合式(8),可得:
(41)
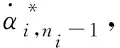
(42)
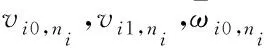
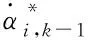
(43)
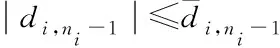
进而,式(41)可进一步重写为:
(44)
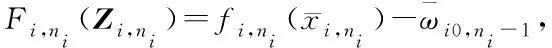
(45)
根据Young′s不等式,结合引理4,则有:
此时,构建Lyapunov函数:
(47)
根据引理1,可得:
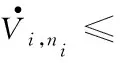
(48)
由式(48)可得控制律和更新律:
(49)
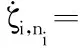
(50)
(51)
将式(49)~(51)代入式(48),可得:
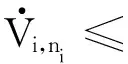
(52)
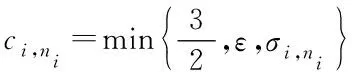
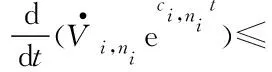
(53)
式(53)两边同乘以eci,nit,可得:

对式(54)两边同时积分,可得:
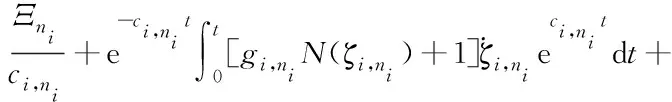
(55)
4 稳定性分析
为了验证所设计的协同容错控制器的主要结果,现给出以下定理。
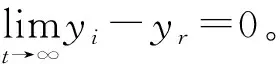
证明:构建多智能体编队系统的Lyapunov函数,如式(54)所示。
(56)
对式(56)求导,整理化简可得:
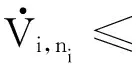
(57)
式(57)可进一步化简为:
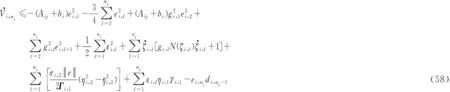
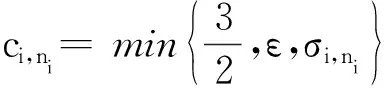

(59)
式中,Ξni/ci,ni为正常数。
根据式(18)~(19)、式(34)~(35)以及式(50)~(51),结合式(57)可知,所有信号参数有界。虚拟控制律和实际控制律均为有界的。同时,联立式(58)和式(59),可知,跟踪误差ei,ni也为零,即多智能体的轨迹与参考轨迹重合。因此,不仅证明了多智能体系统状态均有界,而且证明了在时间t多智能体的运动轨迹与参考轨迹重合。
□
5 数值仿真
为了验证在执行器故障和未知控制方向复合约束下的容错控制方法,利用四组智能体编队子系统进行有限时间容错控制仿真实验,其中每个编队子系统含有4个智能体。为了解决复合约束情形下模型不确定性和反步法中的计算复杂性问题,采用鲁棒自适应模糊技术和一阶滑模积分器进行处理。
本节采用典型的含有执行器故障类型中的偏执故障和未知控制方向的二阶非线性系统及实际工程应用中“领航者-跟随者”无人机编队系统进行实验。
实例1针对实验过程中的多智能体系统,考虑二阶非线性系统模型,如式(60)所示。
(60)
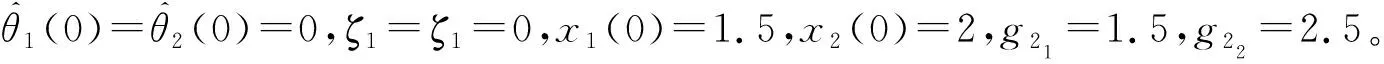
(61)
(62)
除此之外,本节以单组智能体编队作为被控对象,且单组之间的智能体为同构,具有相同的特性,其有向拓扑结构如图1所示。
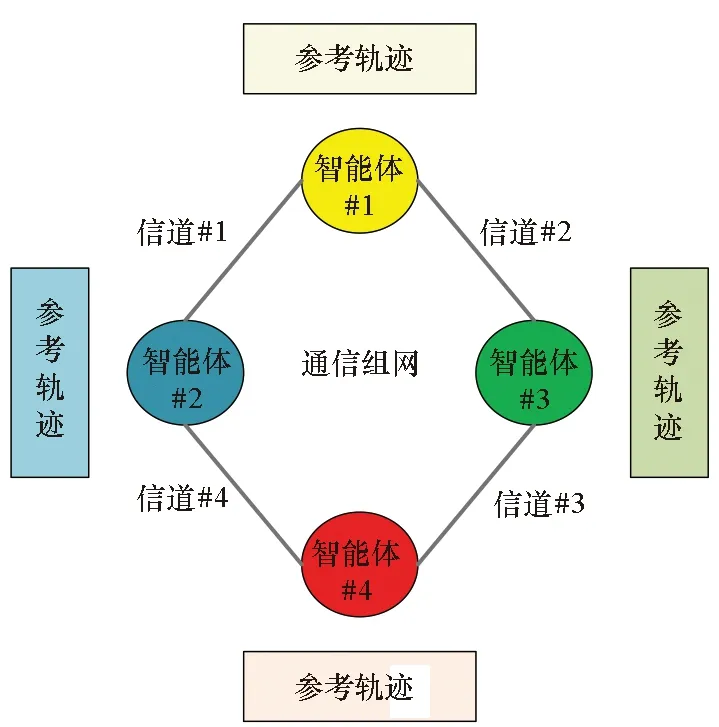
图1 单组多智能体编队网络拓扑图Fig.1 Single-group multi-agent formation network topology diagram
根据上述的初值设定和假设,其仿真结果如图2~4所示。
由图2可知,所提出的基于鲁棒自适应模糊技术的协同容错控制方法,使得智能体依旧按照预设的轨迹小误差范围运动,保持良好的稳定特性。同时,通过引入一阶滑模微分器,将追踪误差逐渐趋于零,提高受限情形下系统的容错性能。
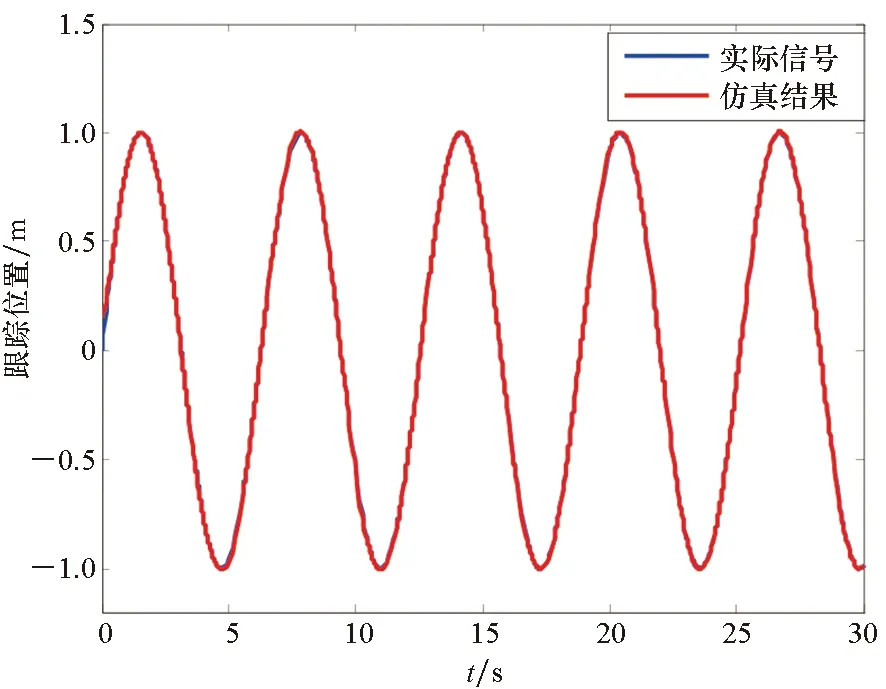
图2 智能体位置跟踪信号曲线Fig.2 Agent position tracking signal curve
由图3和图4可知,针对非线性多智能体中含有混合执行器故障和多未知控制方向的问题,基于自适应模糊技术,提出的容错控制方法能够使多智能体系统模型参数最终趋于零。
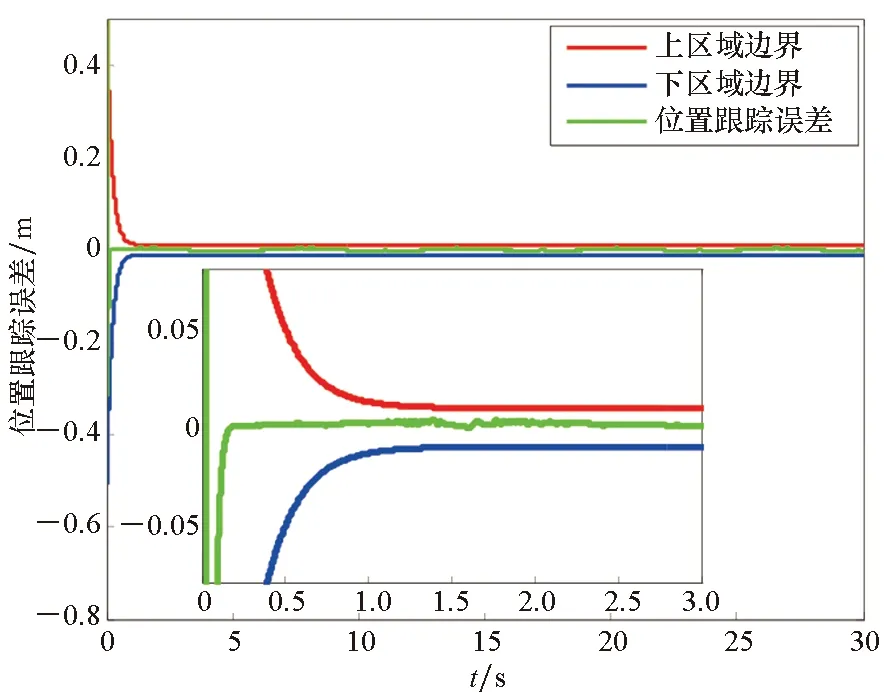
图3 多智能体系统跟踪误差性能曲线Fig.3 Multi-agent system tracking error performance curve
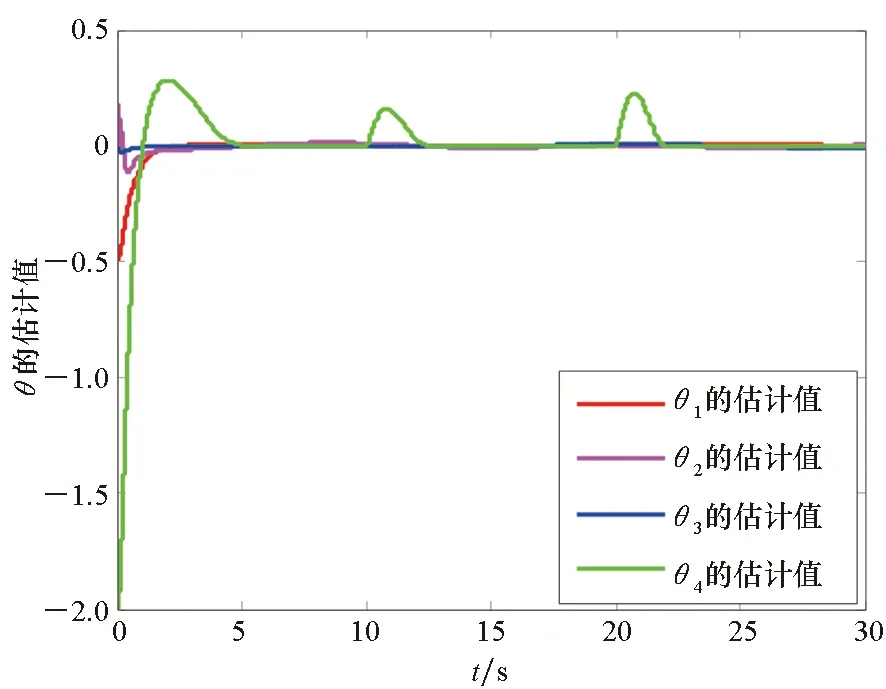
图4 估计参数θi(i=1, 2, 3, 4)的曲线Fig.4 Estimated parameter θi (i=1, 2, 3, 4) curve
实例2为了进一步说明容错控制方法的有效性和适用性,将1个组的编队子系统扩展为4个组的编队子系统以作为被控对象,即4个组构成的编队系统以同时4个组也具有相同的特性,属于同构智能体编队。机器人编队中领航者和跟随者的动力学模型如式(63)和式(64)所示。
(63)
其中,l表示领航者。
(64)
其中,i=1,2,3,…,16,变量的含义与系统模型式(8)一致。仿真初值设定为:Mi=2 kg,vi(0)=0.5 m/s,xi,1(0)=0.5,xi,2(0)=-0.5。设置参考轨迹为:pix=10t,piy=10sin(0.5t),同时每个智能体的初始位置(pi0,pi0)和对应的指定位置(δix,δiy)的取值见表2。

表2 仿真实验参数
其拓扑结构如图5所示。根据初值设定和假设,其仿真实验结果如图6~8所示。
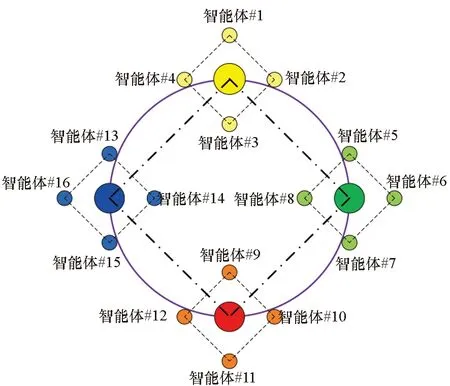
图5 4组多智能体编队系统网络拓扑结构图Fig.5 Network topology structure diagram of 4 groups of multi-agent formation system
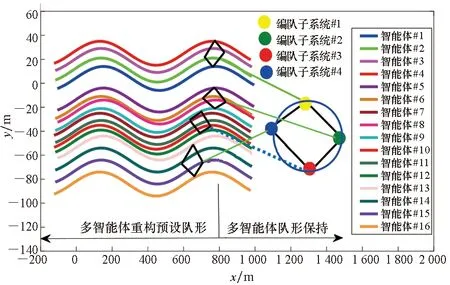
图6 4个编队子系统的运动轨迹曲线Fig.6 Trajectory curves of 4 formation subsystems
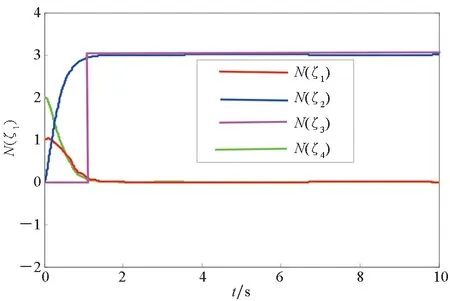
图7 4种情形下的Nussbaum函数曲线图Fig.7 Nussbaum function curves in 4 situations
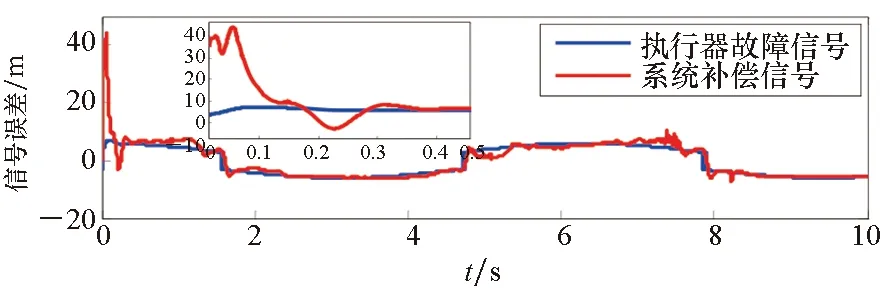
图8 多智能体系统在执行器故障下的容错性能曲线Fig.8 Fault-tolerant performance curve of multi-agent system under actuator fault
由图6可知,控制方法能够提高在执行器故障和未知控制方向共存情形下的容错性能。图7针对具有多未知控制方向的多智能体系统,采用分段Nussbaum函数进行处理,结合鲁棒自适应模糊技术减小追踪误差,提高控制精度,进而改善在故障情形下的容错性能。图8、图9解决了在混合执行器故障和未知控制方向复合控制情形下的容错控制问题,其位置跟踪误差变化小,而且补偿效果良好。
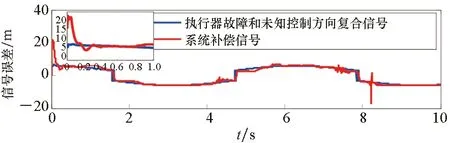
图9 多智能体系统在复合约束下的容错性能曲线Fig.9 Fault-tolerant performance curve of multi-agent system under compound constraints
6 结论
本文针对一类典型的非线性多智能体系统中存在混合执行器故障和多未知控制方向的复合约束问题提出了一种基于鲁棒自适应模糊技术的新颖的协同容错控制方法。该方法将分段Nussbaum函数和鲁棒自适应技术结合起来,分别对多未知控制方向和混合执行器故障进行处理,同时利用一阶滑模积分器简化容错控制律的设计过程,将追踪误差限定在预设的允差范围之类,提高了在不同编队结构系统中追踪误差的控制精度和收敛速度。此外,将多智能体规模从由4个智能体组成的单组编队系统扩展为由16个智能体组成的4组编队系统,验证了本文算法的有效性和合理性。主要的贡献如下:
1)提出基于鲁棒自适应模糊控制的协同容错方案,以补偿多种类型的执行器故障损失,而无须任何故障检测和隔离机制。本文控制方法可以补偿多种类型的执行器故障,并且使系统成功稳定下来。此外,即使在执行器出现故障的情况下,该方法也可以确保输出的有界性。因此,可以实现有效、低成本和可靠的系统控制设计的目标。
2)首次研究了针对不确定多智能体系统具有混合执行器故障和部分控制方向未知相结合的问题;基于分段Nussbaum 函数方法解决了,部分控制增益未知、部分控制增益已知的问题。本研究更具普遍性以及更高的实际应用价值。
3)区别于传统反步技术以及传统动态面反步方法,将一阶滑模微分器技术与反步技术相结合,该方法不仅能够有效地规避冗余的虚拟控制律求导中的“计算爆炸”问题,并且忽略有限时间收敛特性同时满足分离原理,具有更好的控制性能,有利于在实际系统中的应用。
4)在系统设计虚拟控制律过程中,加入鲁棒有界估计方法,利用双曲正切函数的有界性,为参数估计值设定估计界,能够有效地减小系统输出和参考轨迹之间的误差,不仅增强了系统的鲁棒性,而且提高了系统的追踪精度。该方法具有适用范围广、跟踪精度高、容错性能强等优点。

